3.3.2简单的线性规划问题1
文档属性
| 名称 | 3.3.2简单的线性规划问题1 |  | |
| 格式 | zip | ||
| 文件大小 | 498.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-10-12 16:46:54 | ||
图片预览







文档简介
(共21张PPT)
3.3.2简单的线性规划问题(一)
⑴ 二元一次不等式表示平面区域:
复习回顾:
相应直线某一侧(有时可包含直线本身)所有点组成的平面区域.
⑵ 判定方法:
直线定界,特殊点定域,虚实分明.
⑶ 二元一次不等式组表示平面区域:
各个不等式所表示平面区域的公共部分.
某工厂用A、B两种配件生产甲、乙两种产品,每生产一件甲产品使用4个A配件耗时1h,每生产一件乙产品使用4个B配件耗时2h,该厂最多可从配件厂获得16个A配件和12个B配件,按每天工作8h计算,该厂所有的日生产安排是什么?
解析:(1) 从实际问题中抽象出不等式组:
(2)将上述不等式组表示成平面上的区域.
探究引入:
消耗量
产品类型
甲产品
乙产品
A配件
B配件
时间
4
0
4
1
2
0
资源限额
16
12
8
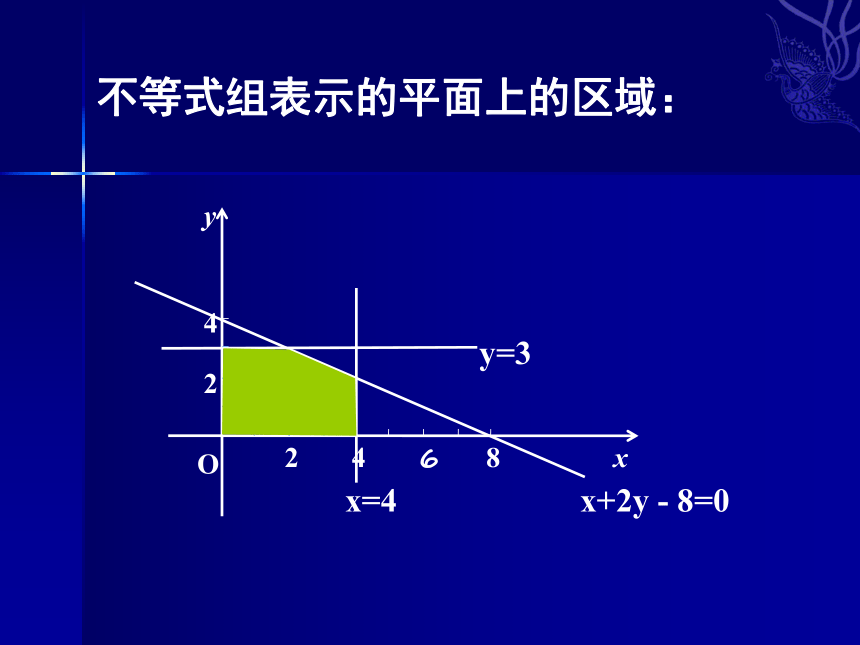
不等式组表示的平面上的区域:
O
2
4
6
8
2
4
y
x
x+2y - 8=0
x=4
y=3
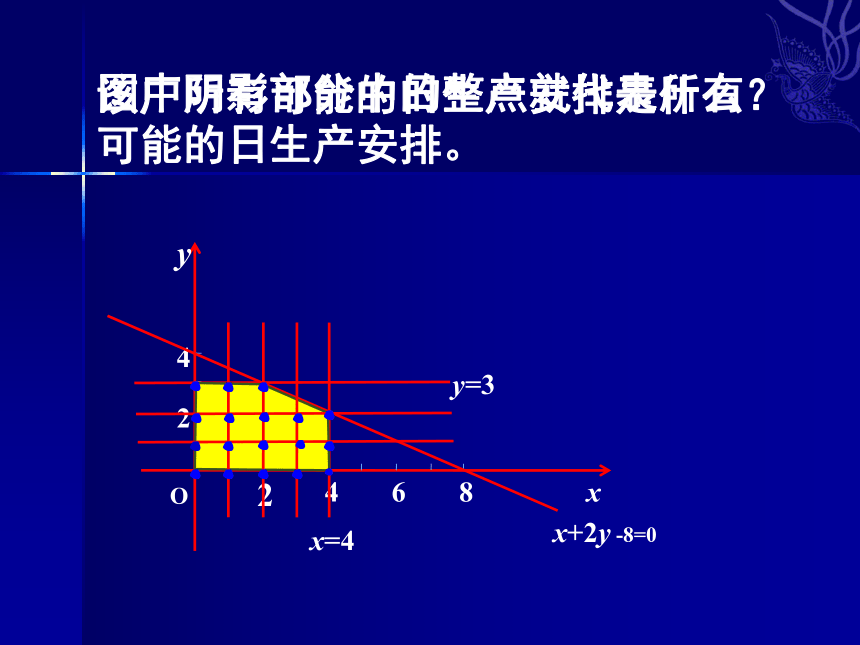
图中阴影部分中的整点就代表所有
可能的日生产安排。
O
2
4
6
8
2
4
y
x
x+2y -8=0
x=4
y=3
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
该厂所有可能的日生产安排是什么?
某工厂用A、B两种配件生产甲、乙两种产品,每生产一件甲产品使用4个A配件耗时1h,每生产一件乙产品使用4个B配件耗时2h,该厂最多可从配件厂获得16个A配件和12个B配件,按每天工作8h计算,若生产一件甲产品获利2万元,生产一件乙产品获利3万元,采用哪种生产安排利润最大?
探究问题:
所以,我们就有必要来探求与Z的取值密切相关的几何因素有哪些?
当然,我们可以把这些整点坐标一一代入,求出Z后比较得出最大值,可这里有18个点,工作量比较大,如果区域再大些呢?
思考:利润z=2x+3y,在x,y满足上述
不等式组的前提下,z的最大值该怎么求?
探究过程:
O
2
4
6
8
2
4
y
x
x+2y -8=0
x=4
y=3
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
O
2
4
6
8
2
4
y
x
x+2y -8=0
x=4
y=3
·
·
P
M
问题 1: 将z=2x+3y变形
问题 2: z/3几何意义_______________________________ .
斜率为-2/3的直线在y轴上截距.
问题 3: z的最值怎样求 .
点定线,线定截距,截距定z
P(1,2)
将Z看成常数。
最优解:使目标函数达到最大值或 最小值 的可行解.
线性约束条件:约束条件中均为关于x、y的一次 不等式或方程.
约束条件:由x、y的不等式(方程)构成 的不等式组.
目标函数:欲求最值的关于x、y的解析式.
线性目标函数:欲求最值的解析式是关于x、y的 一次解析式.
线性规划:求线性目标函数在线性约束条件 下的最大值或最小值.
可行解:满足线性约束条件的解(x,y).
可行域:所有可行解组成的集合.
知识梳理:
解线性规划问题的步骤:
2、 在线性目标函数所表示的一组平行线
中,用平移的方法找出与可行域有公
共点且纵截距最大或最小的直线;
3、 通过解方程组求出最优解;
4、 作出答案。
1、 画出线性约束条件所表示的可行域;
画
移
求
答
小结提炼:
在上述问题中,若生产一件甲产品获利m万元,生产一件乙产品获利n万元,采用哪种生产安排利润最大?
变式探究一:
m
n
3
2
1
2
3
1
O
2
4
6
8
2
4
y
x
x+2y -8=0
x=4
y=3
·
M
Z的最大值是不是还在M点处取得呢?
·
N
变式探究二:
求z=x-y的最大值与最小值,使式中的 x、y满足约束条件:
O
2
6
8
2
4
y
x
x+2y -8=0
x=4
y=3
·
P
Q
·
解:1.画出可行域;
2. 作直线 : y= x ,
平移 ,当 经过可行域上
点P时,-z 最大,即 z最小.
平移 ,当 经过可行域上
点Q时,-z 最小,即 z最大.
3.易得P(0,3),Q(4,0)
4.
z=x-y
y=x-z
M
N
探究过程:
在这里为什么往左上方平移直线使截距越大,z反而越小呢?
分析:对于函数 可变形为
当B为正时,截距 越大,z的取值也越大。
当B为负时, 截距 越大, z的取值反而越小。
当B为正时,在可行域内平移目标函数线,往右上方平移使截距最大,z取到最大值,往左下方平移使截距最小,z取到最小值。
当B为负时,在可行域内平移目标函数线,
往左上方平移使截距最大,z取到最小值,
往右下方平移使截距最小,z取到最大值。
对于目标函数 ,如画好了
方法技巧:
课堂总结:
线性规划问题的有关概念;
用图解法解线性规划问题的一般 步骤及技巧;
本节课所用到的数学思想与方法.
阅读《必修5》P.87-P.88;
《必修5》P.91面练习第1题(2);
设z=2x-y,式中变量x、y满足下列条件 求z的最大值和最小值。
课后作业:
线性目标函数的最大值、最小值一般在可行域的顶点处取得;
线性目标函数的最大值、最小值也可在可行域的边界处取得(此时最优解有多个);
线性目标函数的最大值、最小值也可在可行域的内部取得(如整点问题,待学).
随着目标函数线的斜率的变化,其最值点的取得也呈现多样性.
释疑:
设z=2x+y,求满足
时,求z的最大值和最小值.
线性目标函数
线性约束条件
线性规划问题
任何一个满足不等式组的(x,y)
可行解
可行域
所有的
最优解
使z取最大值
使z取最小值
二元一次不等式 表示平面区域
直线定界, 特殊点定域
简单的线性规划
约束条件
目标函数
可行解
可行域
最优解
应用
求解方法:
画、移、求、答
3.3.2简单的线性规划问题(一)
⑴ 二元一次不等式表示平面区域:
复习回顾:
相应直线某一侧(有时可包含直线本身)所有点组成的平面区域.
⑵ 判定方法:
直线定界,特殊点定域,虚实分明.
⑶ 二元一次不等式组表示平面区域:
各个不等式所表示平面区域的公共部分.
某工厂用A、B两种配件生产甲、乙两种产品,每生产一件甲产品使用4个A配件耗时1h,每生产一件乙产品使用4个B配件耗时2h,该厂最多可从配件厂获得16个A配件和12个B配件,按每天工作8h计算,该厂所有的日生产安排是什么?
解析:(1) 从实际问题中抽象出不等式组:
(2)将上述不等式组表示成平面上的区域.
探究引入:
消耗量
产品类型
甲产品
乙产品
A配件
B配件
时间
4
0
4
1
2
0
资源限额
16
12
8
不等式组表示的平面上的区域:
O
2
4
6
8
2
4
y
x
x+2y - 8=0
x=4
y=3
图中阴影部分中的整点就代表所有
可能的日生产安排。
O
2
4
6
8
2
4
y
x
x+2y -8=0
x=4
y=3
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
该厂所有可能的日生产安排是什么?
某工厂用A、B两种配件生产甲、乙两种产品,每生产一件甲产品使用4个A配件耗时1h,每生产一件乙产品使用4个B配件耗时2h,该厂最多可从配件厂获得16个A配件和12个B配件,按每天工作8h计算,若生产一件甲产品获利2万元,生产一件乙产品获利3万元,采用哪种生产安排利润最大?
探究问题:
所以,我们就有必要来探求与Z的取值密切相关的几何因素有哪些?
当然,我们可以把这些整点坐标一一代入,求出Z后比较得出最大值,可这里有18个点,工作量比较大,如果区域再大些呢?
思考:利润z=2x+3y,在x,y满足上述
不等式组的前提下,z的最大值该怎么求?
探究过程:
O
2
4
6
8
2
4
y
x
x+2y -8=0
x=4
y=3
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
O
2
4
6
8
2
4
y
x
x+2y -8=0
x=4
y=3
·
·
P
M
问题 1: 将z=2x+3y变形
问题 2: z/3几何意义_______________________________ .
斜率为-2/3的直线在y轴上截距.
问题 3: z的最值怎样求 .
点定线,线定截距,截距定z
P(1,2)
将Z看成常数。
最优解:使目标函数达到最大值或 最小值 的可行解.
线性约束条件:约束条件中均为关于x、y的一次 不等式或方程.
约束条件:由x、y的不等式(方程)构成 的不等式组.
目标函数:欲求最值的关于x、y的解析式.
线性目标函数:欲求最值的解析式是关于x、y的 一次解析式.
线性规划:求线性目标函数在线性约束条件 下的最大值或最小值.
可行解:满足线性约束条件的解(x,y).
可行域:所有可行解组成的集合.
知识梳理:
解线性规划问题的步骤:
2、 在线性目标函数所表示的一组平行线
中,用平移的方法找出与可行域有公
共点且纵截距最大或最小的直线;
3、 通过解方程组求出最优解;
4、 作出答案。
1、 画出线性约束条件所表示的可行域;
画
移
求
答
小结提炼:
在上述问题中,若生产一件甲产品获利m万元,生产一件乙产品获利n万元,采用哪种生产安排利润最大?
变式探究一:
m
n
3
2
1
2
3
1
O
2
4
6
8
2
4
y
x
x+2y -8=0
x=4
y=3
·
M
Z的最大值是不是还在M点处取得呢?
·
N
变式探究二:
求z=x-y的最大值与最小值,使式中的 x、y满足约束条件:
O
2
6
8
2
4
y
x
x+2y -8=0
x=4
y=3
·
P
Q
·
解:1.画出可行域;
2. 作直线 : y= x ,
平移 ,当 经过可行域上
点P时,-z 最大,即 z最小.
平移 ,当 经过可行域上
点Q时,-z 最小,即 z最大.
3.易得P(0,3),Q(4,0)
4.
z=x-y
y=x-z
M
N
探究过程:
在这里为什么往左上方平移直线使截距越大,z反而越小呢?
分析:对于函数 可变形为
当B为正时,截距 越大,z的取值也越大。
当B为负时, 截距 越大, z的取值反而越小。
当B为正时,在可行域内平移目标函数线,往右上方平移使截距最大,z取到最大值,往左下方平移使截距最小,z取到最小值。
当B为负时,在可行域内平移目标函数线,
往左上方平移使截距最大,z取到最小值,
往右下方平移使截距最小,z取到最大值。
对于目标函数 ,如画好了
方法技巧:
课堂总结:
线性规划问题的有关概念;
用图解法解线性规划问题的一般 步骤及技巧;
本节课所用到的数学思想与方法.
阅读《必修5》P.87-P.88;
《必修5》P.91面练习第1题(2);
设z=2x-y,式中变量x、y满足下列条件 求z的最大值和最小值。
课后作业:
线性目标函数的最大值、最小值一般在可行域的顶点处取得;
线性目标函数的最大值、最小值也可在可行域的边界处取得(此时最优解有多个);
线性目标函数的最大值、最小值也可在可行域的内部取得(如整点问题,待学).
随着目标函数线的斜率的变化,其最值点的取得也呈现多样性.
释疑:
设z=2x+y,求满足
时,求z的最大值和最小值.
线性目标函数
线性约束条件
线性规划问题
任何一个满足不等式组的(x,y)
可行解
可行域
所有的
最优解
使z取最大值
使z取最小值
二元一次不等式 表示平面区域
直线定界, 特殊点定域
简单的线性规划
约束条件
目标函数
可行解
可行域
最优解
应用
求解方法:
画、移、求、答
