2021-2022学年湘教版九年级数学上册期末复习综合检测试题(word版含答案)
文档属性
| 名称 | 2021-2022学年湘教版九年级数学上册期末复习综合检测试题(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 357.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-02 19:42:02 | ||
图片预览



文档简介
2021-2022学年湘教版九年级数学上册期末复习综合检测试题
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共10小题,共30分)
已知点在反比例函数的图象上,则下列各点一定在该图象上的是
A. B. C. D.
两个相似三角形的面积比为,那么它们的对应边的比为
A. B. C. D.
某农科院对甲、乙两种甜玉米各用块相同条件的试验田进行试验,得到两个品种每公顷产量的两组数据,其方差分别为,,则
A. 甲比乙的产量稳定 B. 乙比甲的产量稳定
C. 甲、乙的产量一样稳定 D. 无法确定哪一品种的产量更稳定
计算的结果为
A. B. C. D.
关于的一元二次方程有实数根,则的取值范围是
A. B. 且
C. D. 且
下列四组条件中,能判定∽的是
A. ,,
B. ,,,,
C. ,,,,
D. ,,,,
如图,在中,,,,则下列不正确的是
A. B. C. D.
如图,将矩形沿对角线折叠,使点落在点处,交于点,则下列结论不一定成立的是
A. ∽
B.
C.
D.
若一元二次方程有两个不相等的实数根,,且,则的值是
A. B. C. 或 D. 或
如图, 的对角线,交于点,平分交于点,交于点,,,连接下列结论: 平分,其中正确的有
A. 个 B. 个 C. 个 D. 个
二、填空题(本大题共8小题,共24分)
已知双曲线经过点,那么的值等于 .
某校开展“节约每一滴水”活动,为了了解开展活动一个月以来节约用水的情况,从八年级的名同学中选取名同学统计了各自家庭一个月节约用水的情况,如下表:
节水量
家庭数个
请你估计这名同学的家庭一个月节约用水的总量大约是 .
我们把直角坐标系中横坐标与纵坐标都是整数的点称为整点反比例函数的图象上有一些整点,请写出其中一个整点的坐标 .
已知在平面直角坐标系中,点,,,以原点为位似中心将缩小,位似比为,则点的对应点的坐标为 .
已知是方程的一个根,则代数式 的值为 .
如图,在中,点,,分别在,,上,,若,,,则的长为 .
如图,是一块正三角形余料,边长为,要把它加工成正方形零件,使正方形的一边在边上,其余两个顶点、分别在、上,则这个正方形零件的边长是 .
如图,将一个直角的顶点放在矩形的对角线上滑动,并使其一条直角边始终经过点,另一条直角边与边相交于点,且,,则 .
三、解答题(本大题共8小题,共66分)
解下列方程:
.
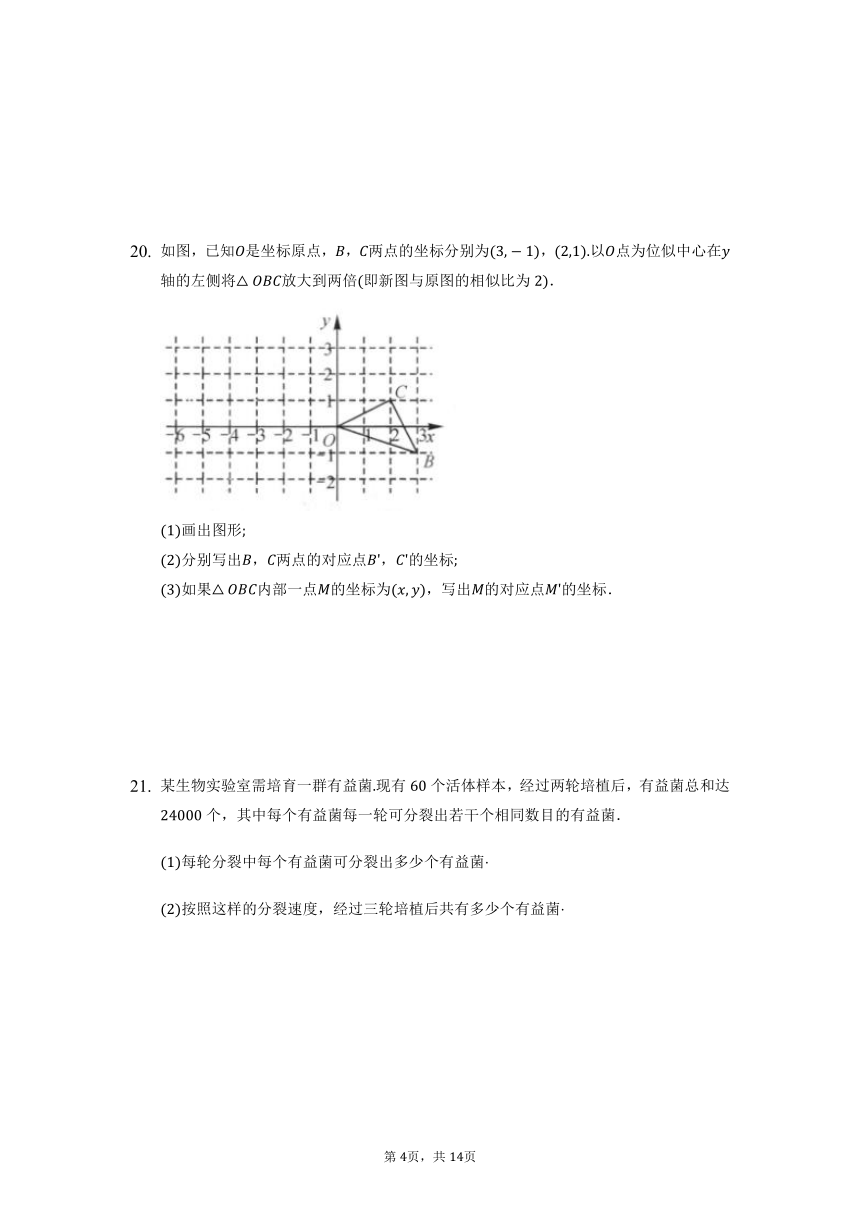
如图,已知是坐标原点,,两点的坐标分别为,以点为位似中心在轴的左侧将放大到两倍即新图与原图的相似比为.
画出图形
分别写出,两点的对应点,的坐标
如果内部一点的坐标为,写出的对应点的坐标.
某生物实验室需培育一群有益菌现有个活体样本,经过两轮培植后,有益菌总和达个,其中每个有益菌每一轮可分裂出若干个相同数目的有益菌.
每轮分裂中每个有益菌可分裂出多少个有益菌
按照这样的分裂速度,经过三轮培植后共有多少个有益菌
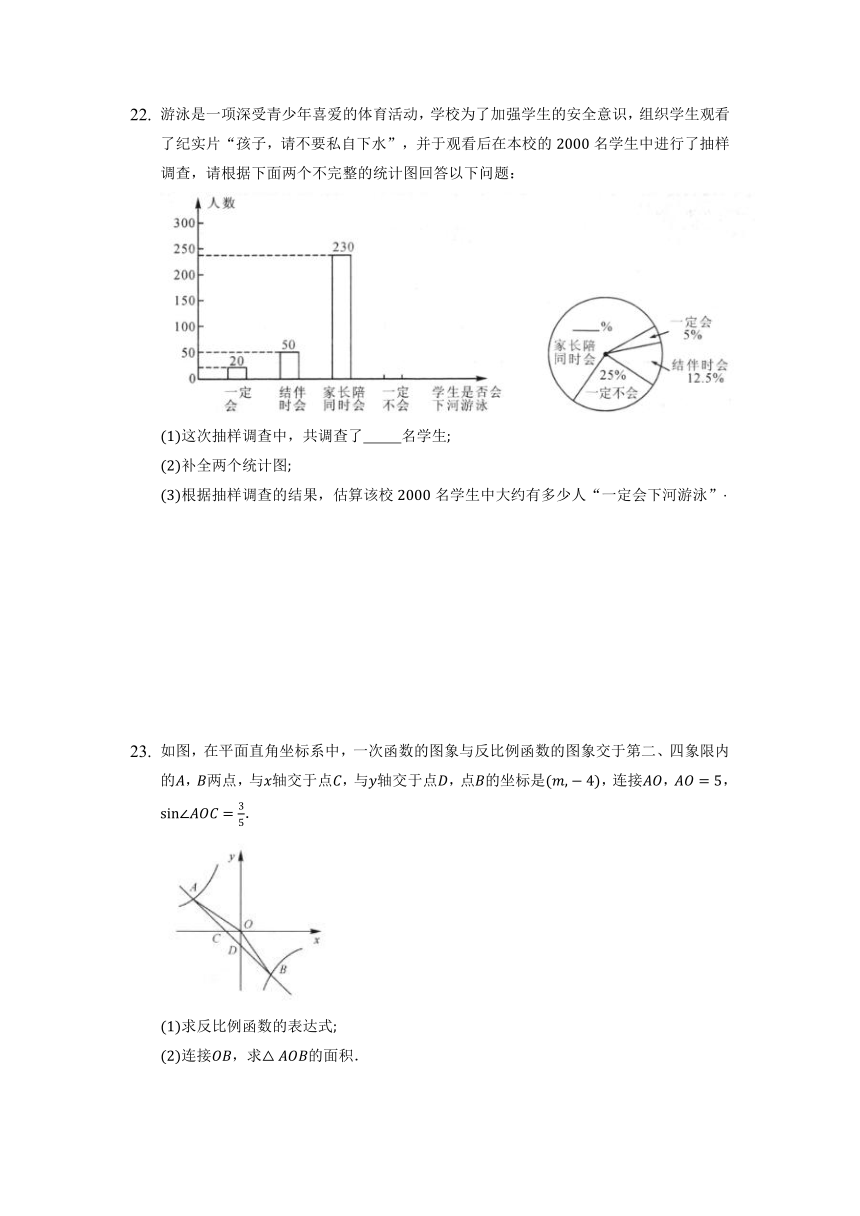
游泳是一项深受青少年喜爱的体育活动,学校为了加强学生的安全意识,组织学生观看了纪实片“孩子,请不要私自下水”,并于观看后在本校的名学生中进行了抽样调查,请根据下面两个不完整的统计图回答以下问题:
这次抽样调查中,共调查了 名学生
补全两个统计图
根据抽样调查的结果,估算该校名学生中大约有多少人“一定会下河游泳”
如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象交于第二、四象限内的,两点,与轴交于点,与轴交于点,点的坐标是,连接,,.
求反比例函数的表达式
连接,求的面积.
如图,在中,,垂足为,,垂足为,与相交于点,连接.
求证:∽
若,,,求的长.
为了维护海洋权益,国家海洋局加大了在南海的巡逻力度,一天,两艘海监船刚好在某岛东西海岸线上的,两处巡逻,同时发现一艘不明国籍的船只停在处海域,如图所示,海里,在处测得在北偏东的方向上,在处测得在北偏西的方向上,在海岸线上有一灯塔,测得海里.
分别求出与及与的距离,结果保留根号
已知在灯塔周围海里范围内有暗礁群,在处的海监船沿前往处盘查,途中有无触礁的危险参考数据:,,
如图,在矩形中,,,将的顶点在矩形的边上滑动,在滑动过程中始终保持,射线经过点,射线交直线于点,交直线于点.
求证:∽
在点的运动过程中,点与点能重合吗如果能重合,求的长
是否存在这样的点,使的面积等于面积的倍若存在,求出的长若不存在,请说明理由.
答案和解析
1.【答案】
【解析】解:点在反比例函数的图象上,
.
,
也在反比例函数的图象上.
故选 D.
2.【答案】
3.【答案】
4.【答案】
5.【答案】
【解析】关于的一元二次方程 有实数根,
,
即,
解得,
又,
的取值范围是且
故选D.
6.【答案】
7.【答案】
8.【答案】
9.【答案】
10.【答案】
【解析】在 中, ,
,.
平分,
.
,
是等边三角形,
.
,
,
,
,
,
,
即,
,故正确
,,
,
平分,故正确
在中,,
,故错误
是的中点,是的中点,
是的中位线,
,,
,,
∽,
,且,
,
,故错误.
故选B.
11.【答案】
12.【答案】
13.【答案】答案不唯一,如:,,,
14.【答案】或
15.【答案】
【解析】解:是方程的一个根,
,
,
.
16.【答案】
17.【答案】
【解析】点拨:如图,作的高,交于点.
为正三角形,
,
由勾股定理得 .
设正方形的边长为,
则,
.
,
∽,.
即,
解得.
加工成的正方形零件的边长是.
18.【答案】
19.【答案】解:,.
,.
20.【答案】解:
,.
的坐标为.
21.【答案】设每轮分裂中每个有益菌可分裂出个有益菌,根据题意,得
.
解得,不合题意,舍去.
答:每轮分裂中每个有益菌可分裂出个有益菌.
个.
答:经过三轮培植后共有个有益菌.
【解析】见答案
22.【答案】解:;
;
该校名学生中大约有人“一定会下河游泳”.
23.【答案】解:过点作轴于点,
,
在中,,,
,,
点的坐标为,
设反比例函数表达式为,
点在反比例函数的图象上,
,解得,
反比例函数表达式为.
点在反比例函数的图象上,
,解得,
点的坐标为.
设直线的表达式为,将,代入,得
解得
一次函数表达式为,
令一次函数中,则,解得,
点的坐标为,
..
24.【答案】解:证明:,,
,
,
∽.
∽,
,
,
,,
,
,
,
,
,
,
,
∽,
,
,
.
25.【答案】解:如图,过点作于点,可得,,设海里,则在中,海里,海里.
在中,海里,海里.
,,
解得.
海里,海里.
如图,过点作于点,可得.
在中,,
海里海里.
途中无触礁的危险.
【解析】求解是否触礁或是否受台风或噪声影响等问题的方法:一般都是求出暗礁中心到航线的距离,或城市中心目标中心到台风中心的距离,或学校到噪声源的距离,将这些距离与暗礁半径或台风影响半径或噪声影响半径比较大小,距离小于或等于半径有危险或有影响,距离大于半径没有危险或没有影响.
26.【答案】解:证明:四边形是矩形,.
.
又,
.
.
∽.
在点的运动过程中,点能与点重合,当,重合时,
,
.
又,
.
又,
∽.
.
解得或.
,重合时的长为或.
存在.
∽,
根据的面积等于面积的倍,得到两三角形的相似比为,
则有,解得.
第2页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共10小题,共30分)
已知点在反比例函数的图象上,则下列各点一定在该图象上的是
A. B. C. D.
两个相似三角形的面积比为,那么它们的对应边的比为
A. B. C. D.
某农科院对甲、乙两种甜玉米各用块相同条件的试验田进行试验,得到两个品种每公顷产量的两组数据,其方差分别为,,则
A. 甲比乙的产量稳定 B. 乙比甲的产量稳定
C. 甲、乙的产量一样稳定 D. 无法确定哪一品种的产量更稳定
计算的结果为
A. B. C. D.
关于的一元二次方程有实数根,则的取值范围是
A. B. 且
C. D. 且
下列四组条件中,能判定∽的是
A. ,,
B. ,,,,
C. ,,,,
D. ,,,,
如图,在中,,,,则下列不正确的是
A. B. C. D.
如图,将矩形沿对角线折叠,使点落在点处,交于点,则下列结论不一定成立的是
A. ∽
B.
C.
D.
若一元二次方程有两个不相等的实数根,,且,则的值是
A. B. C. 或 D. 或
如图, 的对角线,交于点,平分交于点,交于点,,,连接下列结论: 平分,其中正确的有
A. 个 B. 个 C. 个 D. 个
二、填空题(本大题共8小题,共24分)
已知双曲线经过点,那么的值等于 .
某校开展“节约每一滴水”活动,为了了解开展活动一个月以来节约用水的情况,从八年级的名同学中选取名同学统计了各自家庭一个月节约用水的情况,如下表:
节水量
家庭数个
请你估计这名同学的家庭一个月节约用水的总量大约是 .
我们把直角坐标系中横坐标与纵坐标都是整数的点称为整点反比例函数的图象上有一些整点,请写出其中一个整点的坐标 .
已知在平面直角坐标系中,点,,,以原点为位似中心将缩小,位似比为,则点的对应点的坐标为 .
已知是方程的一个根,则代数式 的值为 .
如图,在中,点,,分别在,,上,,若,,,则的长为 .
如图,是一块正三角形余料,边长为,要把它加工成正方形零件,使正方形的一边在边上,其余两个顶点、分别在、上,则这个正方形零件的边长是 .
如图,将一个直角的顶点放在矩形的对角线上滑动,并使其一条直角边始终经过点,另一条直角边与边相交于点,且,,则 .
三、解答题(本大题共8小题,共66分)
解下列方程:
.
如图,已知是坐标原点,,两点的坐标分别为,以点为位似中心在轴的左侧将放大到两倍即新图与原图的相似比为.
画出图形
分别写出,两点的对应点,的坐标
如果内部一点的坐标为,写出的对应点的坐标.
某生物实验室需培育一群有益菌现有个活体样本,经过两轮培植后,有益菌总和达个,其中每个有益菌每一轮可分裂出若干个相同数目的有益菌.
每轮分裂中每个有益菌可分裂出多少个有益菌
按照这样的分裂速度,经过三轮培植后共有多少个有益菌
游泳是一项深受青少年喜爱的体育活动,学校为了加强学生的安全意识,组织学生观看了纪实片“孩子,请不要私自下水”,并于观看后在本校的名学生中进行了抽样调查,请根据下面两个不完整的统计图回答以下问题:
这次抽样调查中,共调查了 名学生
补全两个统计图
根据抽样调查的结果,估算该校名学生中大约有多少人“一定会下河游泳”
如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象交于第二、四象限内的,两点,与轴交于点,与轴交于点,点的坐标是,连接,,.
求反比例函数的表达式
连接,求的面积.
如图,在中,,垂足为,,垂足为,与相交于点,连接.
求证:∽
若,,,求的长.
为了维护海洋权益,国家海洋局加大了在南海的巡逻力度,一天,两艘海监船刚好在某岛东西海岸线上的,两处巡逻,同时发现一艘不明国籍的船只停在处海域,如图所示,海里,在处测得在北偏东的方向上,在处测得在北偏西的方向上,在海岸线上有一灯塔,测得海里.
分别求出与及与的距离,结果保留根号
已知在灯塔周围海里范围内有暗礁群,在处的海监船沿前往处盘查,途中有无触礁的危险参考数据:,,
如图,在矩形中,,,将的顶点在矩形的边上滑动,在滑动过程中始终保持,射线经过点,射线交直线于点,交直线于点.
求证:∽
在点的运动过程中,点与点能重合吗如果能重合,求的长
是否存在这样的点,使的面积等于面积的倍若存在,求出的长若不存在,请说明理由.
答案和解析
1.【答案】
【解析】解:点在反比例函数的图象上,
.
,
也在反比例函数的图象上.
故选 D.
2.【答案】
3.【答案】
4.【答案】
5.【答案】
【解析】关于的一元二次方程 有实数根,
,
即,
解得,
又,
的取值范围是且
故选D.
6.【答案】
7.【答案】
8.【答案】
9.【答案】
10.【答案】
【解析】在 中, ,
,.
平分,
.
,
是等边三角形,
.
,
,
,
,
,
,
即,
,故正确
,,
,
平分,故正确
在中,,
,故错误
是的中点,是的中点,
是的中位线,
,,
,,
∽,
,且,
,
,故错误.
故选B.
11.【答案】
12.【答案】
13.【答案】答案不唯一,如:,,,
14.【答案】或
15.【答案】
【解析】解:是方程的一个根,
,
,
.
16.【答案】
17.【答案】
【解析】点拨:如图,作的高,交于点.
为正三角形,
,
由勾股定理得 .
设正方形的边长为,
则,
.
,
∽,.
即,
解得.
加工成的正方形零件的边长是.
18.【答案】
19.【答案】解:,.
,.
20.【答案】解:
,.
的坐标为.
21.【答案】设每轮分裂中每个有益菌可分裂出个有益菌,根据题意,得
.
解得,不合题意,舍去.
答:每轮分裂中每个有益菌可分裂出个有益菌.
个.
答:经过三轮培植后共有个有益菌.
【解析】见答案
22.【答案】解:;
;
该校名学生中大约有人“一定会下河游泳”.
23.【答案】解:过点作轴于点,
,
在中,,,
,,
点的坐标为,
设反比例函数表达式为,
点在反比例函数的图象上,
,解得,
反比例函数表达式为.
点在反比例函数的图象上,
,解得,
点的坐标为.
设直线的表达式为,将,代入,得
解得
一次函数表达式为,
令一次函数中,则,解得,
点的坐标为,
..
24.【答案】解:证明:,,
,
,
∽.
∽,
,
,
,,
,
,
,
,
,
,
,
∽,
,
,
.
25.【答案】解:如图,过点作于点,可得,,设海里,则在中,海里,海里.
在中,海里,海里.
,,
解得.
海里,海里.
如图,过点作于点,可得.
在中,,
海里海里.
途中无触礁的危险.
【解析】求解是否触礁或是否受台风或噪声影响等问题的方法:一般都是求出暗礁中心到航线的距离,或城市中心目标中心到台风中心的距离,或学校到噪声源的距离,将这些距离与暗礁半径或台风影响半径或噪声影响半径比较大小,距离小于或等于半径有危险或有影响,距离大于半径没有危险或没有影响.
26.【答案】解:证明:四边形是矩形,.
.
又,
.
.
∽.
在点的运动过程中,点能与点重合,当,重合时,
,
.
又,
.
又,
∽.
.
解得或.
,重合时的长为或.
存在.
∽,
根据的面积等于面积的倍,得到两三角形的相似比为,
则有,解得.
第2页,共2页
同课章节目录
