福建省四地六校2013届高三上学期第一次月考 数学文试题
文档属性
| 名称 | 福建省四地六校2013届高三上学期第一次月考 数学文试题 |  | |
| 格式 | zip | ||
| 文件大小 | 273.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-10-12 18:08:30 | ||
图片预览



文档简介
“华安、连城、永安、漳平一中、龙海二中、泉港一中”六校联考
2012-2013学年上学期第一次月考
高三文科数学试卷
(考试时间:120分钟 总分:150分)
选择题(本题共12个小题,每小题5分,共60分。在每小题给出的四个选项中,只有一个项是符合要求的)。
1.设全集<,集合,则等于( )
A. B. C. D.
2. 已知条件,条件,则成立的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既非充分也非必要条件
3.的值为( )
A. B. C. D.
4.如果,那么( )
A. B. C. D.
5.若a>0>b>-a,c<d<0,则下列命题①ad>bc,②<0,③a-c>b-d,④a(d-c)>b(d-c)中能成立的个数是( )
A.1 B.2 C.3 D.4
6.下列函数中,既是偶函数又在单调递增的函数是 ( )
A. B. C. D.
7.已知某等差数列共有10项,其奇数项之和为15,偶数项之和为30,则其公差为( )
A.2 B.3 C.4 D.521世纪教育网
8.设等比数列中,前n项和为 ( )
A. B. C. D.
9.函数的值域是
(A) (B)
(C) (D)
10.将函数y=sin2x的图象向右平移个单位,再向上平移1个单位,所得函数图象对应的解析式为( )
A. B.
C. D.
11.已知函数,则对任意,若,下列不等式成立的是( )
A. B.
C. D.
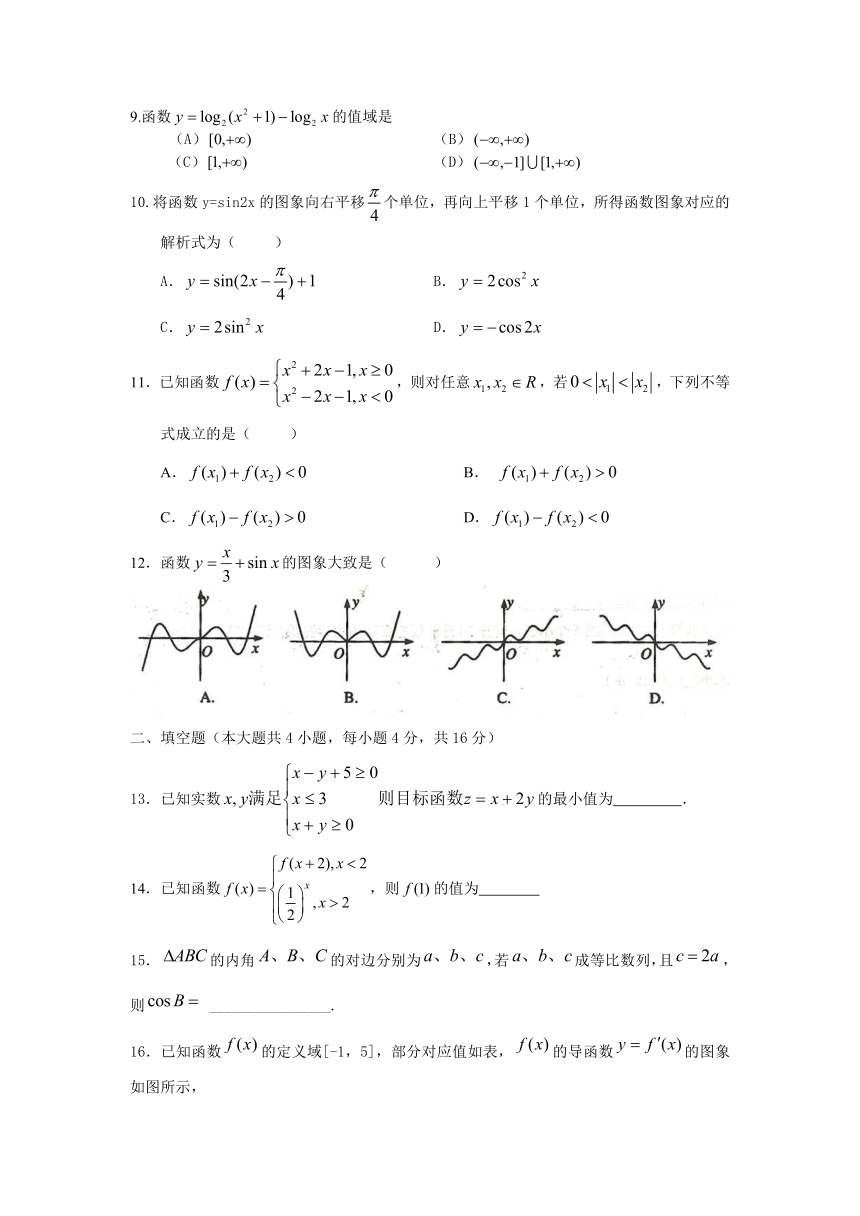
12.函数的图象大致是( )
二、填空题(本大题共4小题,每小题4分,共16分)
13.已知实数的最小值为 .
14.已知函数,则的值为
15. 的内角的对边分别为,若成等比数列,且,则 ________________.
16.已知函数的定义域[-1,5],部分对应值如表,的导函数的图象如图所示,
下列关于函数的命题;
①函数的值域为[1,2];
②函数在[0,2]上是减函数;
③如果当时,的最大值是2,那么t的最大值为4;
④当有4个零点。
其中真命题为 (填写序号)
解答题(本大题共6小题,共74分。解答应写出文字说明、证明过程或演算步骤)
17.(本题满分12分)已知中,内角的对边分别为,且,. 21世纪教育网
(Ⅰ)求的值;
(Ⅱ)设,求的面积.
18.(本题满分12分)已知等差数列,公差d大于0,且是方程的两个根,数列的前n项和为。
(1)求数列、的通项公式;
(2)记
19.(本题满分12分)函数f(x)=Asin(ωx+φ) (A>0,ω>0,|φ|<)的部分图象如图所示.
(1)求f(x)的最小正周期及解析式;
(2)设g(x)=f(x)-cos 2x,求函数g(x)在区间[0,]上的最大值和最小值.
20. 某产品原来的成本为1000元/件,售价为1200元/件,年销售量为1万件。由于市场饱和顾客要求提高,公司计划投入资金进行产品升级。据市场调查,若投入万元,每件产品的成本将降低元,在售价不变的情况下,年销售量将减少万件,按上述方式进行产品升级和销售,扣除产品升级资金后的纯利润记为(单位:万元).(纯利润=每件的利润×年销售量-投入的成本)
⑴求的函数解析式;
⑵求的最大值,以及取得最大值时的值.
21.(本题满分12分)已知等差数列中,,,数列中,,.
(I)求数列的通项公式,写出它的前项和;
(II)求数列的通项公式;
(III)若,求数列的前项和.
22.(本小题满分14分)
已知函数,是常数.
求函数的图象在点处的切线的方程,并证明函数()的图象在直线的下方;
讨论函数零点的个数.
参考答案
1-6 DBACCB 7-12 BACCDC
13、 -3 14、 15、 16、②
17.解:(Ⅰ)∵为的内角,且,,
∴
……………21世纪教育网……………………4分
∴
………………………………………6分
(Ⅱ)由(I)知, ∴ ……………………………7分
∵,由正弦定理得
………………21世纪教育网………………10分
∴ …………………………………12分
18.解:(1)设的公差为d,由题意得:
……………………4分
………7分
(2)
…………………………………………12分
19.解答:(1)由图可得A=1,,所以T=π。ω=2………………3分
当x=时,f(x)=1,可得sin(2×+φ)=1
∵|φ|<,∴φ=。∴f(x)=sin(2x+)…………………21世纪教育网…………………6分
g(x)=f(x)-cos2x =sin(2x+)-cos2x =sin2x cos+cos2x sin-cos2x
=sin2x-cos2x =sin(2x-)………………………………9分
∵0≤x≤,∴-≤2x-≤。
当2x-=,即x=时,g(x)有最大值为1;
当2x-=-,即x=0时,g(x)有最小值为-……………………………………12分
解:⑴依题意,
产品升级后,每件的成本为元,利润为元…………2分,
年销售量为万件……………………………3分,
纯利润为………………………………………5分,
(万元)……………………………………7分
⑵……9分,
………………………………………21世纪教育网…………10分,
等号当且仅当……11分,即(万元)……12分。
21.解:(I)设,由题意得,,
所以,; ……3分
(II),,
所以,,……………………5分
()
又时,
所以数列的通项; ……7分
(III)
21世纪教育网…12分
22.解:(1),,所以切线的方程为
,即.……………………………………3分
作,,则
-
↗ 最大值 ↘
,解得.
所以且,,,即函数()的图像在直线的下方.…………………………………………………7分
法一
令y=0,即lnx=ax-1,画图可知
当a≤0时,直线y=ax-1与y=lnx的图像有且只有一个交点,即一个零点;……8分
当a>0时,设直线y=ax-1与y=lnx切于点(x0,lnx0),切线斜率为k=
∴切线方程为y-lnx0=(x-x0),把(0,-1)代入上式可得x0=1,k=1…………9分
∴当0<a<1时,直线y=ax-1与y=lnx有两个交点,即两个零点;………………10分
当a=1时直线y=ax-1与y=lnx相切于一点,即一个零点;………………………11分
当a>1时直线y=ax-1与y=lnx没有交点,即无零点。……………………………12分
综上可知,当时,无零点;当或时,有且仅有一个零点;当时,有两个零点.…………………………………………………………14分
法二
⑵有零点,即有解, ……………………8分
,解得,类似⑴列表讨论知,即若有零点,则;若,则无零点.………………………………………………9分
若,,由⑴知有且仅有一个零点.………………10分
若,单调递增,由幂函数与对数函数单调性比较知有且仅有一个零点(或:直线与曲线有一个交点)………………………11分
若,解得,类似⑴列表讨论知,在处取最大值,,由幂函数与对数函数单调性比较知,………………12分
当充分大时,即在单调递减区间有且仅有一个零点;又因为,所以在单调递增区间有且仅有一个零点,…………13分
综上所述,当时,无零点;当或时,有且仅有一个零点;当时,有两个零点.……………………………………………………………14分
其余解法酌情给分。
2012-2013学年上学期第一次月考
高三文科数学试卷
(考试时间:120分钟 总分:150分)
选择题(本题共12个小题,每小题5分,共60分。在每小题给出的四个选项中,只有一个项是符合要求的)。
1.设全集<,集合,则等于( )
A. B. C. D.
2. 已知条件,条件,则成立的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既非充分也非必要条件
3.的值为( )
A. B. C. D.
4.如果,那么( )
A. B. C. D.
5.若a>0>b>-a,c<d<0,则下列命题①ad>bc,②<0,③a-c>b-d,④a(d-c)>b(d-c)中能成立的个数是( )
A.1 B.2 C.3 D.4
6.下列函数中,既是偶函数又在单调递增的函数是 ( )
A. B. C. D.
7.已知某等差数列共有10项,其奇数项之和为15,偶数项之和为30,则其公差为( )
A.2 B.3 C.4 D.521世纪教育网
8.设等比数列中,前n项和为 ( )
A. B. C. D.
9.函数的值域是
(A) (B)
(C) (D)
10.将函数y=sin2x的图象向右平移个单位,再向上平移1个单位,所得函数图象对应的解析式为( )
A. B.
C. D.
11.已知函数,则对任意,若,下列不等式成立的是( )
A. B.
C. D.
12.函数的图象大致是( )
二、填空题(本大题共4小题,每小题4分,共16分)
13.已知实数的最小值为 .
14.已知函数,则的值为
15. 的内角的对边分别为,若成等比数列,且,则 ________________.
16.已知函数的定义域[-1,5],部分对应值如表,的导函数的图象如图所示,
下列关于函数的命题;
①函数的值域为[1,2];
②函数在[0,2]上是减函数;
③如果当时,的最大值是2,那么t的最大值为4;
④当有4个零点。
其中真命题为 (填写序号)
解答题(本大题共6小题,共74分。解答应写出文字说明、证明过程或演算步骤)
17.(本题满分12分)已知中,内角的对边分别为,且,. 21世纪教育网
(Ⅰ)求的值;
(Ⅱ)设,求的面积.
18.(本题满分12分)已知等差数列,公差d大于0,且是方程的两个根,数列的前n项和为。
(1)求数列、的通项公式;
(2)记
19.(本题满分12分)函数f(x)=Asin(ωx+φ) (A>0,ω>0,|φ|<)的部分图象如图所示.
(1)求f(x)的最小正周期及解析式;
(2)设g(x)=f(x)-cos 2x,求函数g(x)在区间[0,]上的最大值和最小值.
20. 某产品原来的成本为1000元/件,售价为1200元/件,年销售量为1万件。由于市场饱和顾客要求提高,公司计划投入资金进行产品升级。据市场调查,若投入万元,每件产品的成本将降低元,在售价不变的情况下,年销售量将减少万件,按上述方式进行产品升级和销售,扣除产品升级资金后的纯利润记为(单位:万元).(纯利润=每件的利润×年销售量-投入的成本)
⑴求的函数解析式;
⑵求的最大值,以及取得最大值时的值.
21.(本题满分12分)已知等差数列中,,,数列中,,.
(I)求数列的通项公式,写出它的前项和;
(II)求数列的通项公式;
(III)若,求数列的前项和.
22.(本小题满分14分)
已知函数,是常数.
求函数的图象在点处的切线的方程,并证明函数()的图象在直线的下方;
讨论函数零点的个数.
参考答案
1-6 DBACCB 7-12 BACCDC
13、 -3 14、 15、 16、②
17.解:(Ⅰ)∵为的内角,且,,
∴
……………21世纪教育网……………………4分
∴
………………………………………6分
(Ⅱ)由(I)知, ∴ ……………………………7分
∵,由正弦定理得
………………21世纪教育网………………10分
∴ …………………………………12分
18.解:(1)设的公差为d,由题意得:
……………………4分
………7分
(2)
…………………………………………12分
19.解答:(1)由图可得A=1,,所以T=π。ω=2………………3分
当x=时,f(x)=1,可得sin(2×+φ)=1
∵|φ|<,∴φ=。∴f(x)=sin(2x+)…………………21世纪教育网…………………6分
g(x)=f(x)-cos2x =sin(2x+)-cos2x =sin2x cos+cos2x sin-cos2x
=sin2x-cos2x =sin(2x-)………………………………9分
∵0≤x≤,∴-≤2x-≤。
当2x-=,即x=时,g(x)有最大值为1;
当2x-=-,即x=0时,g(x)有最小值为-……………………………………12分
解:⑴依题意,
产品升级后,每件的成本为元,利润为元…………2分,
年销售量为万件……………………………3分,
纯利润为………………………………………5分,
(万元)……………………………………7分
⑵……9分,
………………………………………21世纪教育网…………10分,
等号当且仅当……11分,即(万元)……12分。
21.解:(I)设,由题意得,,
所以,; ……3分
(II),,
所以,,……………………5分
()
又时,
所以数列的通项; ……7分
(III)
21世纪教育网…12分
22.解:(1),,所以切线的方程为
,即.……………………………………3分
作,,则
-
↗ 最大值 ↘
,解得.
所以且,,,即函数()的图像在直线的下方.…………………………………………………7分
法一
令y=0,即lnx=ax-1,画图可知
当a≤0时,直线y=ax-1与y=lnx的图像有且只有一个交点,即一个零点;……8分
当a>0时,设直线y=ax-1与y=lnx切于点(x0,lnx0),切线斜率为k=
∴切线方程为y-lnx0=(x-x0),把(0,-1)代入上式可得x0=1,k=1…………9分
∴当0<a<1时,直线y=ax-1与y=lnx有两个交点,即两个零点;………………10分
当a=1时直线y=ax-1与y=lnx相切于一点,即一个零点;………………………11分
当a>1时直线y=ax-1与y=lnx没有交点,即无零点。……………………………12分
综上可知,当时,无零点;当或时,有且仅有一个零点;当时,有两个零点.…………………………………………………………14分
法二
⑵有零点,即有解, ……………………8分
,解得,类似⑴列表讨论知,即若有零点,则;若,则无零点.………………………………………………9分
若,,由⑴知有且仅有一个零点.………………10分
若,单调递增,由幂函数与对数函数单调性比较知有且仅有一个零点(或:直线与曲线有一个交点)………………………11分
若,解得,类似⑴列表讨论知,在处取最大值,,由幂函数与对数函数单调性比较知,………………12分
当充分大时,即在单调递减区间有且仅有一个零点;又因为,所以在单调递增区间有且仅有一个零点,…………13分
综上所述,当时,无零点;当或时,有且仅有一个零点;当时,有两个零点.……………………………………………………………14分
其余解法酌情给分。
同课章节目录
