福建省四地六校2013届高三上学期第一次月考 数学理试题
文档属性
| 名称 | 福建省四地六校2013届高三上学期第一次月考 数学理试题 |  | |
| 格式 | zip | ||
| 文件大小 | 342.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-10-12 18:08:30 | ||
图片预览



文档简介
“华安、连城、永安、漳平一中、龙海二中、泉港一中”六校联考
2012-2013学年上学期第一次月考
高三数学(理科)试题
(考试时间:120分钟 总分:150分)
第I卷(选择题 共50分)
一、选择题:(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项符合题目要求)
1、已知集合,集合,且,则( )
A. B. C. D.
2、函数的定义域是( )
A. B. C. D.
3、在某个物理实验中,测量得变量和变量的几组数据,如下表:
则对,最适合的拟合函数是 ( )
A. B. C. D.
4、已知函数,则( )
A. B. C. D.
5、设,则( )21世纪教育网
A. B. C. D.
6、设,则函数的零点所在区间为( )
A. B. C. D.
7、下列关于命题的说法错误的是 ( )
A.命题“若,则”的逆否命题为“若,则”;
B.“”是“函数在区间上为增函数”的充分不必要条件;
C.若命题:,则:;
D.命题“ ”是真命题
8、设为实数,函数在处有极值,则曲线在原点处的切线方程为( )
A. B. C. D.
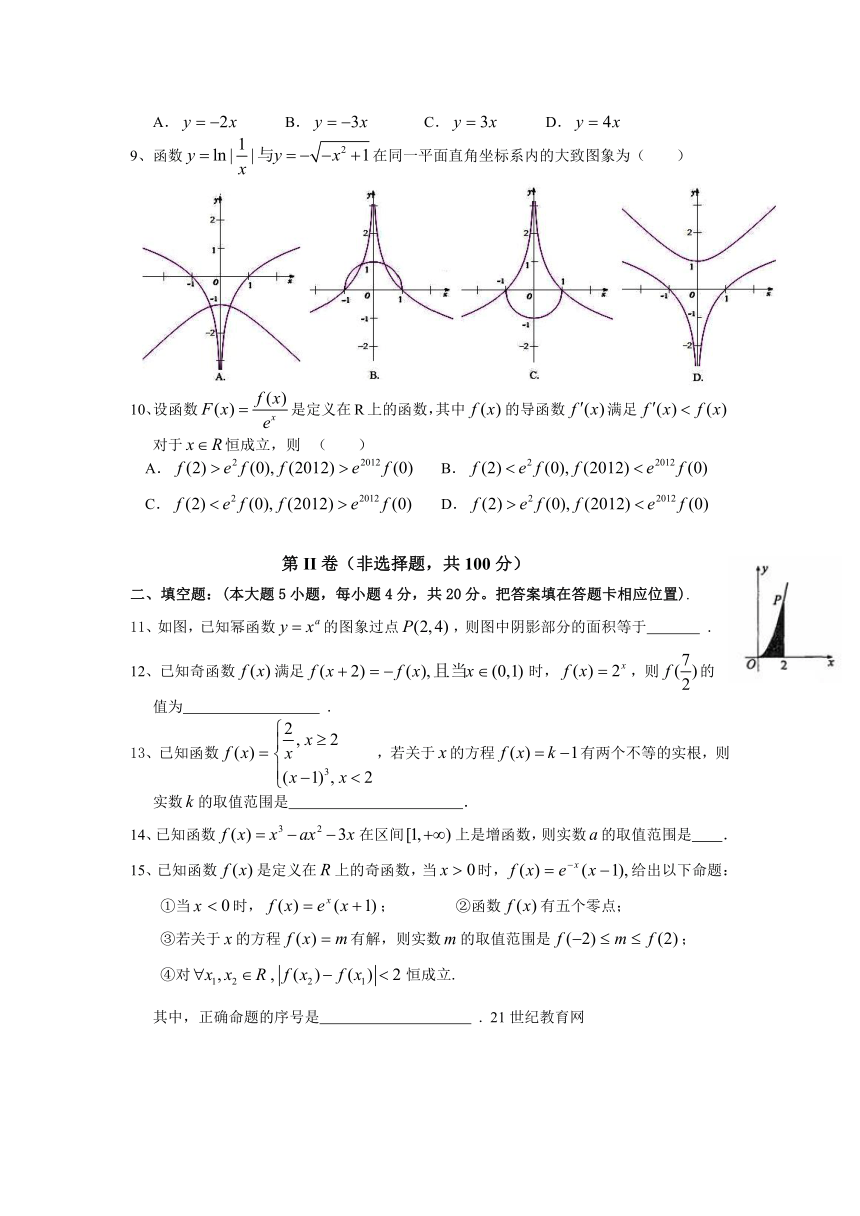
9、函数在同一平面直角坐标系内的大致图象为( )
10、设函数是定义在R上的函数,其中的导函数满足 对于恒成立,则 ( )
A. B.
C. D.
第II卷(非选择题,共100分)
二、填空题:(本大题5小题,每小题4分,共20分。把答案填在答题卡相应位置). K*S&5#U.C︿OM
11、如图,已知幂函数的图象过点,则图中阴影部分的面积等于 .
12、已知奇函数满足时,,则的
值为 .
13、已知函数,若关于的方程有两个不等的实根,则实数的取值范围是 .
14、已知函数在区间上是增函数,则实数的取值范围是 .
15、已知函数是定义在上的奇函数,当时,给出以下命题:
①当时,; ②函数有五个零点;
③若关于的方程有解,则实数的取值范围是;
④对恒成立.
其中,正确命题的序号是 . 21世纪教育网
三、解答题:(本大题共6小题,共80分,解答应写出文字说明、证明过程或演算步骤)
16、(本小题满分13分)
已知集合,,若,求实数的取值范围.
17、(本小题满分13分)
已知命题实数满足,命题实数满足
,若是的必要不充分条件,求实数的取值范围.
18、(本小题满分13分)
已知函数满足,对任意都有,且.
(1)求函数的解析式;
(2)是否存在实数,使函数在上为减函数?若存在,求出实数的取值范围;若不存在,说明理由.
19、(本小题满分13分)
某厂生产某种产品的年固定成本为万元,每生产千件,需另投入成本为.当年产量不足千件时, (万元).当年产量不小于千件时,
(万元).每件商品售价为 万元.通过市场分析,该厂生产的商品能全部售完.
(1)写出年利润 (万元)关于年产量 (千件)的函数解析式;
(2)年产量为多少千件时,该厂在这一商品的生产中所获利润最大?
21世纪教育网
20、(本小题满分14分)
已知函数,
(1)若曲线在点处的切线垂直于轴,求函数 的单调区间;
(2)若函数在区间上无极值,求实数的取值范围.
21、(本小题满分14分)
本题有(1)、(2)、(3)三个选考题,每题7分,请考生任选两题作答,满分14分.如果多做,则按所做的前两题计分.
(1)(本小题满分7分)选修4-2:矩阵与变换
已知矩阵有一个属于特征值的特征向量,
①求矩阵;
②已知矩阵,点,,,求在矩阵的对应变换作用下所得到的的面积.
(2)(本小题满分7分)选修4—4:坐标系与参数方程
已知在直角坐标系中,直线的参数方程为(为参数),在极坐标系(与直角坐标系取相同的长度单位,且以原点为极点,以轴正半轴为极轴)中,曲线的极坐标方程为.
①求直线普通方程和曲线的直角坐标方程;
②设点是曲线上的一个动点,求它到直线的距离的取值范围.
(3)(本小题满分7分)选修4-5:不等式选讲
已知函数
①求不等式的解集;
②若关于的不等式在上恒成立,求实数的取值范围.
21世纪教育网
“华安、连城、永安、漳平一中、龙海二中、泉港一中”六校联考
2012-2013学年上学期第一次月考
高三数学(理科)试题参考答案
一、选择题(本大题共10小题,每小题5分,满分50分.在每小题给出的四个选项中,有且只有一项是符合题目要求的)
题号 1 2 3 4 5 6 7 8 9 10
选项 C B D A A C D B C B
二、填空题(本大题共5小题,每小题4分,满分20分.把答案填在题中相应位置横线上)
11、 12、 13、 14、 15、①④
三、解答题(本大题共6小题,满分80分.解答应写出必要的文字说明 证明过程或演算步骤)
16、解: 由已知得, …………………2分
∵, ∴. …21世纪教育网………3分
又
①当即时, 集合.
要使成立,只需,解得 ……21世纪教育网……………6分
②当即时, ,显然有,所以符合 …………9分
③当即时, 集合.
要使成立,只需,解得 …………………12分
综上所述,所求的取值范围是. …………………13分
17、解 :由,得, …………………3分
∴记
由得,…………………6分
记
∵是的必要不充分条件
∴是的充分不必要条件, 即且, ∴,…………………8分
要使,又,则只需 …………………11分
∴
故所求实数的取值范围是. …………………13分
【另解】由,得, …………………3分
∴记
由得, …………………6分
记
∵是的必要不充分条件
∴且 ∴ 21世纪教育网…………………8分
∴要使,则只需 …………………11分
∴
故所求实数的取值范围是. …………………13分
18、解:(1)由及 ∴ ………………1分
又对任意,有
∴图像的对称轴为直线,则,∴ ………………3分
又对任意都有,
即对任意成立,
∴,故 ………………6分
∴ ………………7分
(2)由(1)知 ,其定义域为……………8分
令
要使函数在上为减函数,
只需函数在上为增函数, ………………10分
由指数函数的单调性,有,解得 ………………12分
故存在实数,当时,函数在上为减函数
………………13分19、解:
(1) 因为每件商品售价为万元,则千件商品销售额为0.05×1000x万元,依题意得:
当0=-x2+40x-250. …21世纪教育网…………2分
当x≥80时,L(x)=(0.05×1000x)-51x-+1450-250
=1200-. ………………4分
所以L(x)= ………………6分
(2)当0此时,当x=60时,L(x)取得最大值L(60)=950万元. ………………9分
当x≥80时,L(x)=1 200-
≤1 200-2 =1 200-200=1000.
此时,当x=时,即x=100时,L(x)取得最大值1000万元.………………12分
∵ 950 < 1000
所以,当产量为100 千件时,该厂在这一商品中所获利润最大,最大利润为1000 万元.
………………13分
20、解:(1)∵
∴ ………………1分
又∵曲线在点处的切线垂直于轴
∴,
由得, ………………3分
∴ ∴
令得,
令得,
∴故的增区间为,减区间为 21世纪教育网………………6分
(2)∵
∴ ………………7分
①当时,在区间上恒成立,即函数在区间上单调递减,故函数在区间上无极值; 21世纪教育网……………9分
②当时,令得:,
当变化时,和的变化情况如下表21世纪教育网
x
+ 0 -
单调递增↗ 极大值 单调递减↘
∴函数在处有极大值,
∴要使函数在区间上无极值,只需, ………………13分
综上①②所述,实数的取值范围为 ………………14分
21、解:(1)解:①由已知得:,
∴ 解得 故. ……………3分
②∵ ……………4分
∴,, ……………6分
即点,,变成点,,
∴的面积为 21世纪教育网…………………7分
(2) 解:①直线的普通方程为:. …………………2分
曲线的直角坐标方程为:【或】.
…………………4分
②曲线的标准方程为,圆心,半径为1;
∴圆心到直线的距离为: …………………6分
所以点到直线的距离的取值范围是 ………………7分
(3)解:①原不等式等价于或或, ……………… 1分
解得
∴不等式的解集为。……………… 4分
②依题意得:关于的不等式在上恒成立,
………………5分
,即,解得
∴实数的取值范围是 21世纪教育网……………7分
2012-2013学年上学期第一次月考
高三数学(理科)试题
(考试时间:120分钟 总分:150分)
第I卷(选择题 共50分)
一、选择题:(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项符合题目要求)
1、已知集合,集合,且,则( )
A. B. C. D.
2、函数的定义域是( )
A. B. C. D.
3、在某个物理实验中,测量得变量和变量的几组数据,如下表:
则对,最适合的拟合函数是 ( )
A. B. C. D.
4、已知函数,则( )
A. B. C. D.
5、设,则( )21世纪教育网
A. B. C. D.
6、设,则函数的零点所在区间为( )
A. B. C. D.
7、下列关于命题的说法错误的是 ( )
A.命题“若,则”的逆否命题为“若,则”;
B.“”是“函数在区间上为增函数”的充分不必要条件;
C.若命题:,则:;
D.命题“ ”是真命题
8、设为实数,函数在处有极值,则曲线在原点处的切线方程为( )
A. B. C. D.
9、函数在同一平面直角坐标系内的大致图象为( )
10、设函数是定义在R上的函数,其中的导函数满足 对于恒成立,则 ( )
A. B.
C. D.
第II卷(非选择题,共100分)
二、填空题:(本大题5小题,每小题4分,共20分。把答案填在答题卡相应位置). K*S&5#U.C︿OM
11、如图,已知幂函数的图象过点,则图中阴影部分的面积等于 .
12、已知奇函数满足时,,则的
值为 .
13、已知函数,若关于的方程有两个不等的实根,则实数的取值范围是 .
14、已知函数在区间上是增函数,则实数的取值范围是 .
15、已知函数是定义在上的奇函数,当时,给出以下命题:
①当时,; ②函数有五个零点;
③若关于的方程有解,则实数的取值范围是;
④对恒成立.
其中,正确命题的序号是 . 21世纪教育网
三、解答题:(本大题共6小题,共80分,解答应写出文字说明、证明过程或演算步骤)
16、(本小题满分13分)
已知集合,,若,求实数的取值范围.
17、(本小题满分13分)
已知命题实数满足,命题实数满足
,若是的必要不充分条件,求实数的取值范围.
18、(本小题满分13分)
已知函数满足,对任意都有,且.
(1)求函数的解析式;
(2)是否存在实数,使函数在上为减函数?若存在,求出实数的取值范围;若不存在,说明理由.
19、(本小题满分13分)
某厂生产某种产品的年固定成本为万元,每生产千件,需另投入成本为.当年产量不足千件时, (万元).当年产量不小于千件时,
(万元).每件商品售价为 万元.通过市场分析,该厂生产的商品能全部售完.
(1)写出年利润 (万元)关于年产量 (千件)的函数解析式;
(2)年产量为多少千件时,该厂在这一商品的生产中所获利润最大?
21世纪教育网
20、(本小题满分14分)
已知函数,
(1)若曲线在点处的切线垂直于轴,求函数 的单调区间;
(2)若函数在区间上无极值,求实数的取值范围.
21、(本小题满分14分)
本题有(1)、(2)、(3)三个选考题,每题7分,请考生任选两题作答,满分14分.如果多做,则按所做的前两题计分.
(1)(本小题满分7分)选修4-2:矩阵与变换
已知矩阵有一个属于特征值的特征向量,
①求矩阵;
②已知矩阵,点,,,求在矩阵的对应变换作用下所得到的的面积.
(2)(本小题满分7分)选修4—4:坐标系与参数方程
已知在直角坐标系中,直线的参数方程为(为参数),在极坐标系(与直角坐标系取相同的长度单位,且以原点为极点,以轴正半轴为极轴)中,曲线的极坐标方程为.
①求直线普通方程和曲线的直角坐标方程;
②设点是曲线上的一个动点,求它到直线的距离的取值范围.
(3)(本小题满分7分)选修4-5:不等式选讲
已知函数
①求不等式的解集;
②若关于的不等式在上恒成立,求实数的取值范围.
21世纪教育网
“华安、连城、永安、漳平一中、龙海二中、泉港一中”六校联考
2012-2013学年上学期第一次月考
高三数学(理科)试题参考答案
一、选择题(本大题共10小题,每小题5分,满分50分.在每小题给出的四个选项中,有且只有一项是符合题目要求的)
题号 1 2 3 4 5 6 7 8 9 10
选项 C B D A A C D B C B
二、填空题(本大题共5小题,每小题4分,满分20分.把答案填在题中相应位置横线上)
11、 12、 13、 14、 15、①④
三、解答题(本大题共6小题,满分80分.解答应写出必要的文字说明 证明过程或演算步骤)
16、解: 由已知得, …………………2分
∵, ∴. …21世纪教育网………3分
又
①当即时, 集合.
要使成立,只需,解得 ……21世纪教育网……………6分
②当即时, ,显然有,所以符合 …………9分
③当即时, 集合.
要使成立,只需,解得 …………………12分
综上所述,所求的取值范围是. …………………13分
17、解 :由,得, …………………3分
∴记
由得,…………………6分
记
∵是的必要不充分条件
∴是的充分不必要条件, 即且, ∴,…………………8分
要使,又,则只需 …………………11分
∴
故所求实数的取值范围是. …………………13分
【另解】由,得, …………………3分
∴记
由得, …………………6分
记
∵是的必要不充分条件
∴且 ∴ 21世纪教育网…………………8分
∴要使,则只需 …………………11分
∴
故所求实数的取值范围是. …………………13分
18、解:(1)由及 ∴ ………………1分
又对任意,有
∴图像的对称轴为直线,则,∴ ………………3分
又对任意都有,
即对任意成立,
∴,故 ………………6分
∴ ………………7分
(2)由(1)知 ,其定义域为……………8分
令
要使函数在上为减函数,
只需函数在上为增函数, ………………10分
由指数函数的单调性,有,解得 ………………12分
故存在实数,当时,函数在上为减函数
………………13分19、解:
(1) 因为每件商品售价为万元,则千件商品销售额为0.05×1000x万元,依题意得:
当0
当x≥80时,L(x)=(0.05×1000x)-51x-+1450-250
=1200-. ………………4分
所以L(x)= ………………6分
(2)当0
当x≥80时,L(x)=1 200-
≤1 200-2 =1 200-200=1000.
此时,当x=时,即x=100时,L(x)取得最大值1000万元.………………12分
∵ 950 < 1000
所以,当产量为100 千件时,该厂在这一商品中所获利润最大,最大利润为1000 万元.
………………13分
20、解:(1)∵
∴ ………………1分
又∵曲线在点处的切线垂直于轴
∴,
由得, ………………3分
∴ ∴
令得,
令得,
∴故的增区间为,减区间为 21世纪教育网………………6分
(2)∵
∴ ………………7分
①当时,在区间上恒成立,即函数在区间上单调递减,故函数在区间上无极值; 21世纪教育网……………9分
②当时,令得:,
当变化时,和的变化情况如下表21世纪教育网
x
+ 0 -
单调递增↗ 极大值 单调递减↘
∴函数在处有极大值,
∴要使函数在区间上无极值,只需, ………………13分
综上①②所述,实数的取值范围为 ………………14分
21、解:(1)解:①由已知得:,
∴ 解得 故. ……………3分
②∵ ……………4分
∴,, ……………6分
即点,,变成点,,
∴的面积为 21世纪教育网…………………7分
(2) 解:①直线的普通方程为:. …………………2分
曲线的直角坐标方程为:【或】.
…………………4分
②曲线的标准方程为,圆心,半径为1;
∴圆心到直线的距离为: …………………6分
所以点到直线的距离的取值范围是 ………………7分
(3)解:①原不等式等价于或或, ……………… 1分
解得
∴不等式的解集为。……………… 4分
②依题意得:关于的不等式在上恒成立,
………………5分
,即,解得
∴实数的取值范围是 21世纪教育网……………7分
同课章节目录
