福建省四地六校2012-2013学年高二上学期第一次月考 数学理试题
文档属性
| 名称 | 福建省四地六校2012-2013学年高二上学期第一次月考 数学理试题 |
|
|
| 格式 | zip | ||
| 文件大小 | 156.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-10-12 00:00:00 | ||
图片预览



文档简介
四地六校联考2012-2013学年上学期第一次月考
高二数学试题
(考试时间:120分钟 总分:150分)
第Ⅰ卷 (选择题 共50分)
一、选择题(本题共10个小题,每小题5分,共50分。在每小题给出的四个选项中,只有一项是符合题目要求的。)
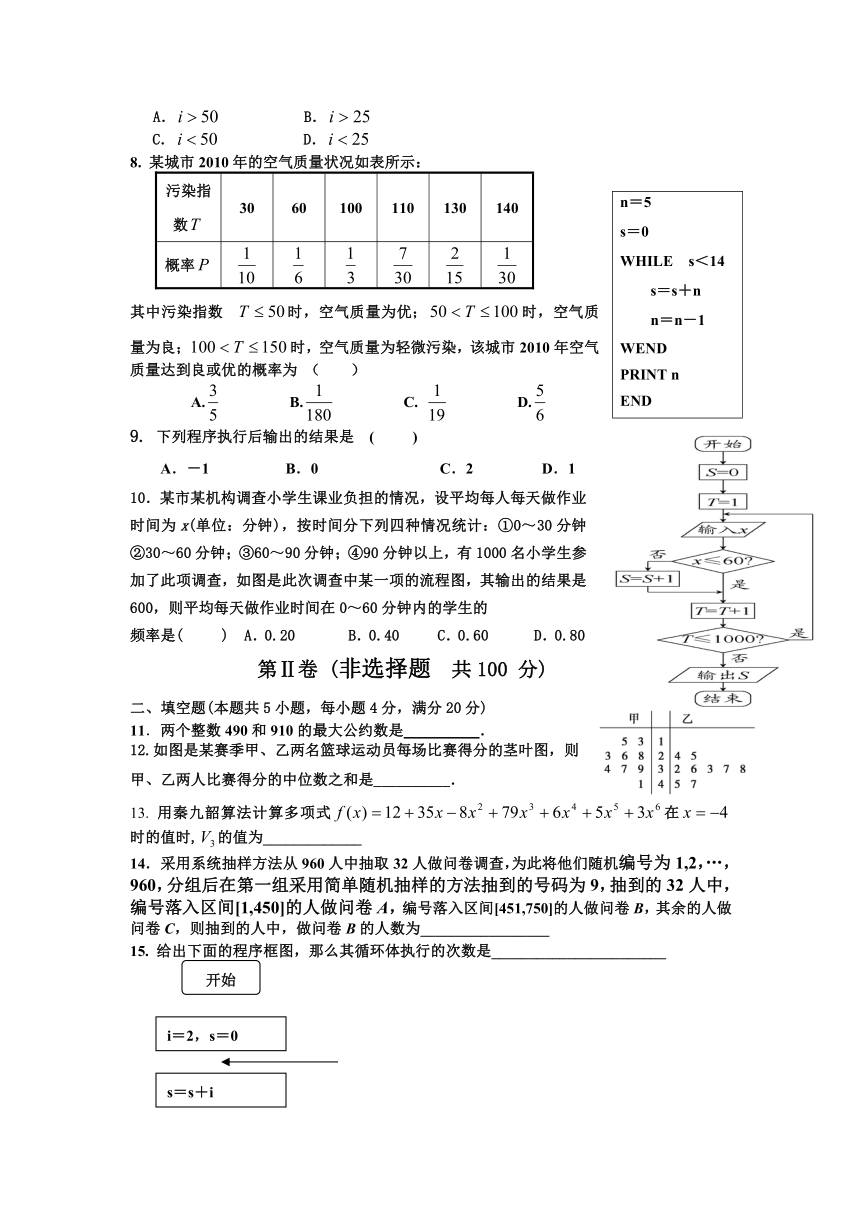
1.如图所示的程序框图输出的结果是( )
(A) (B) (C) (D)
2.某校选修乒乓球课程的学生中,高一年级有30名,高二年级
有40名.现用分层抽样的方法在这70名学生中抽取一个样本,
已知在高一年级的学生中抽取了6名,则在高二年级的学生中应
抽取的人数为( )
A.6 B.8 C.10 D.12
3.将1 010 011化为八进制数为( )
A.123 B.321 C.23 D.32
4.线性回归方程必过( )21世纪教育网
A、(0,0)点 B、(,0)点 C、(0,)点 D、(,)点
5.甲、乙、丙、丁四人参加奥运会射击项目选拔赛,四人的平均成绩和方差如下表所示:
从这四个人中选择一人参加奥运会射击项目比赛,最佳人选是( )
甲 乙 丙 丁
平均环数 8.6 8.9 8.9 8.2
方差s2 3.5 3.5 2.1 5.6
A.甲 B.乙 C.丙 D.丁
6.学校为了调查学生在课外读物方面的支出情况,抽出了一个容量为n且支出在[20,60)元的样本,其频率分布直方图如图所示,其中支出在[50,60)元的同学有30人,则n的值为( )
A.90 B.100 C.900 D.1000
7.右图给出的是计算的值的一个
程序框图,其中判断框内应填入的条件是( )
A. B.
C. D.
8. 某城市2010年的空气质量状况如表所示:
污染指数 30 60 100 110 130 140
概率
n=5s=0WHILE s<14s=s+nn=n-1WENDPRINT nEND
其中污染指数时,空气质量为优;时,空气质量为良;时,空气质量为轻微污染,该城市2010年空气质量达到良或优的概率为 ( )
A. B. C. D.
9. 下列程序执行后输出的结果是 ( )
A.-1 B.0 C.2 D.1
10.某市某机构调查小学生课业负担的情况,设平均每人每天做作业时间为x(单位:分钟),按时间分下列四种情况统计:①0~30分钟②30~60分钟;③60~90分钟;④90分钟以上,有1000名小学生参加了此项调查,如图是此次调查中某一项的流程图,其输出的结果是600,则平均每天做作业时间在0~60分钟内的学生的
频率是( ) A.0.20 B.0.40 C.0.60 D.0.80
第Ⅱ卷 (非选择题 共100 分)
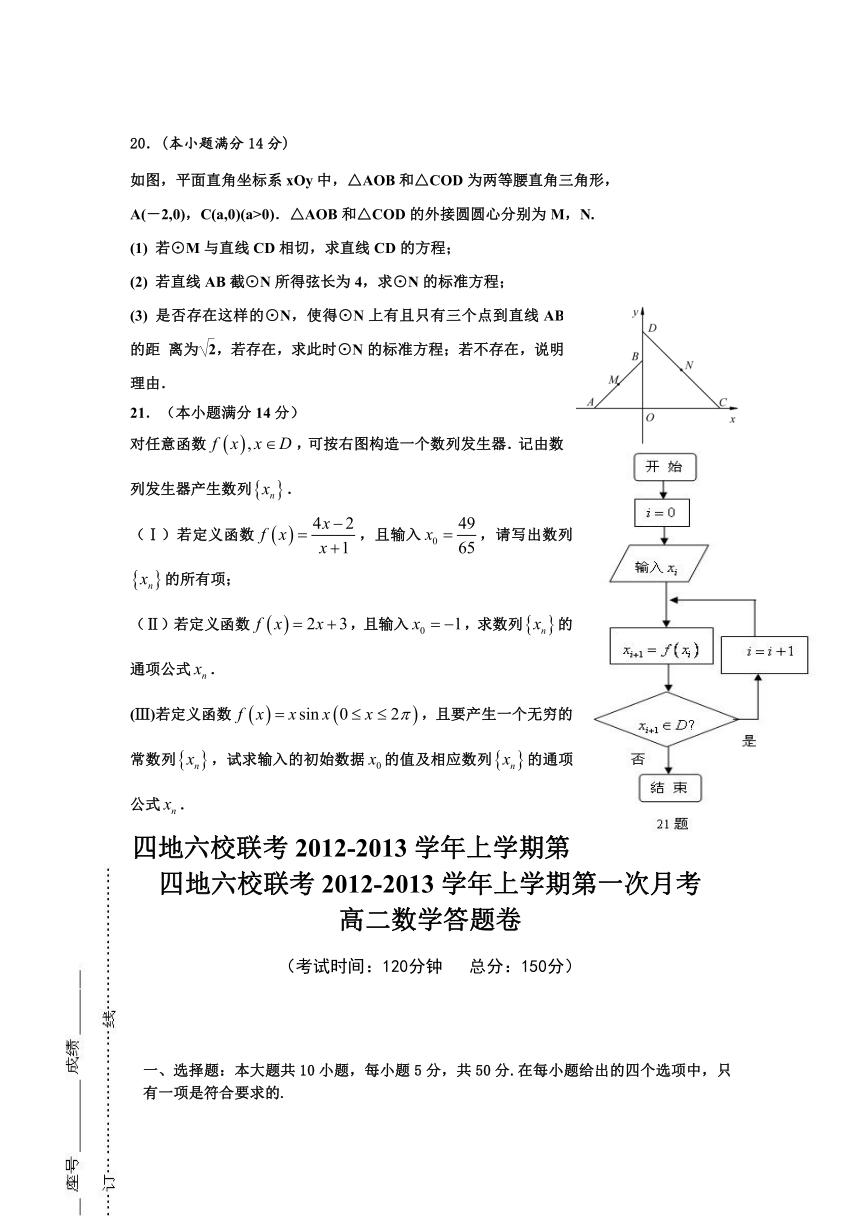
二、填空题(本题共5小题,每小题4分,满分20分)
11.两个整数490和910的最大公约数是 .
12.如图是某赛季甲、乙两名篮球运动员每场比赛得分的茎叶图,则
甲、乙两人比赛得分的中位数之和是__________.
13. 用秦九韶算法计算多项式在时的值时,的值为_____________
14. 采用系统抽样方法从960人中抽取32人做问卷调查,为此将他们随机编号为1,2,…,960,分组后在第一组采用简单随机抽样的方法抽到的号码为9,抽到的32人中,编号落入区间[1,450]的人做问卷A,编号落入区间[451,750]的人做问卷B,其余的人做问卷C,则抽到的人中,做问卷B的人数为_________________
15. 给出下面的程序框图,那么其循环体执行的次数是_______________________
三、解答题(本大题共6个大题,共80分,解答应写出文字说明,证明过程或演算步骤)
16. (本小题满分13分)求倾斜角是直线y=-x+1的倾斜角的,且分别满足下列条件的直线方程: (1)经过点(,-1); (2)在y轴上的截距是-5.
17.(本小题满分13分)
2012年3月2日,国家环保部发布了新修订的《环境空气质量标准》.其中规定:居民区中的PM2.5年平均浓度不得超过35微克/立方米,PM2.5的24小时平均浓度不得超过75微克/立方米. 某城市环保部门随机抽取了一居民区去年40天的PM2.5的24小时平均浓度的监测数据,数据统计如下:
组别 PM2.5(微克/立方米) 频数(天) 频 率
第一组 (0,15] 4 0.1
第二组 (15,30] 12
第三组 (30,45] 8 0.2
第四组 (45,60] 8 0.2
第五组 (60,75] 0.1
第六组 (75,90) 4 0.1
(Ⅰ)试确定的值,并写出该样本的众数和中位数(不必写出计算过程);
(Ⅱ)完成相应的频率分布直方图.
(Ⅲ)求出样本的平均数,并根据样本估计总体的思想,从PM2.5的年平均浓度考虑,判断该居民区的环境是否需要改进?说明理由.
18.(本小题满分13分)
圆C:(x-1)2+(y-2)2=25,直线l:(2m+1)x+(m+1)y-7m-4=0(m∈R).
(1)证明:不论m取什么数,直线l与圆C恒交于两点;
(2)求直线l被圆C截得的线段的最短长度,并求此时m的值.
19.(本小题满分13分)在平面直角坐标系xOy中,曲线y=x2-6x+1与坐标轴的交点都在圆C上.(1)求圆C的方程;21世纪教育网
(2)若圆C与直线x-y+a=0交于A,B两点,且OA⊥OB,求a的值.
20.(本小题满分14分)
如图,平面直角坐标系xOy中,△AOB和△COD为两等腰直角三角形,
A(-2,0),C(a,0)(a>0).△AOB和△COD的外接圆圆心分别为M,N.
(1) 若⊙M与直线CD相切,求直线CD的方程;
(2) 若直线AB截⊙N所得弦长为4,求⊙N的标准方程;
(3) 是否存在这样的⊙N,使得⊙N上有且只有三个点到直线AB的距 离为,若存在,求此时⊙N的标准方程;若不存在,说明理由.
21.(本小题满分14分)
对任意函数,可按右图构造一个数列发生器.记由数列发生器产生数列.
(Ⅰ)若定义函数,且输入,请写出数列的所有项;
(Ⅱ)若定义函数,且输入,求数列的通项公式.
(Ⅲ)若定义函数,且要产生一个无穷的常数列,试求输入的初始数据的值及相应数列的通项公式.
四地六校联考2012-2013学年上学期第四地六校联考2012-2013学年上学期第一次月考
高二数学答题卷
(考试时间:120分钟 总分:150分)
选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合要求的.
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题:本大题共5小题,每小题4分,共20分。
11.__________________ 12.________________ 13._________________
14._____________________ 15._________________
三、解答题(本大题共6小题,共80分)
16. (本小题满分13分)21世纪教育网
17. (本小题满分13分)
18.(本小题满分13分)
19.(本小题满分13分)
20.(本小题满分14分)
21.(本题满分14分)
四地六校联考2012-2013学年上学期第一次月考
高二数学参考答案及评分标准
一、选择题(每小题5分,共50分
题号 1 2 3 4 5 6 7 8 9 10
答案 C B A D C B A A D B
一、选择题(每小题5分,共50分)
二、填空题(本题共5小题,每小题4分,满分20分)
11. 70 12. 64 13. -57
14. 10 15. 49921世纪教育网
三、解答题(本大题共6个大题,共80分,解答应写出文字说明,证明过程或演算步骤)
16. (本小题满分13分)
解:∵直线的方程为y=-x+1,
∴k=-,倾斜角α=120°,
由题知所求直线的倾斜角为30°,即斜率为.…………………………………4分
(1)∵直线经过点(,-1),
∴所求直线方程为y+1=(x-),
即x-3y-6=0. …………………………………9分
(2)∵直线在y轴上的截距为-5,
∴由斜截式知所求直线方程为y=x-5,
即x-3y-15=0. …………………………………13分
17. (本小题满分13分)
解:(Ⅰ),……………………………………………………… 2分
众数为22.5微克/立方米,中位数为37.5微克/立方米.……………………4分
(Ⅱ)其频率分布直方图如图所示:
…21世纪教育网…………………………8分
(Ⅲ)样本的平均数为
……10分
因为,所以去年该居民区PM2.5年平均浓度不符合环境空气质量标准,故该居民区的环境需要改进.……………………………………… 13分
18.(本小题满分13分)
解:(1)证明:∵直线l的方程可化为(2x+y-7)m+(x+y-4)=0(m∈R).
∴l过,的交点M(3,1).
又∵M到圆心C(1,2)的距离为
d==<5,
∴点M(3,1)在圆内,
∴过点M(3,1)的直线l与圆C恒交于两点.…………………………………6分
(2)∵过点M(3,1)的所有弦中,弦心距d≤,
弦心距、半弦长和半径r构成直角三角形,
∴当d2=5时,半弦长的平方的最小值为25-5=20.
∴弦长AB的最小值|AB|min=4.
此时,kCM=-,kl=-.
∵l⊥CM,
∴·=-1,解得m=-.
∴当m=-时,取到最短弦长为4.…………………………………13分
19. (本小题满分13分)
解:(1)曲线y=x2-6x+1与y轴的交点为(0,1),与x轴的交点为(3+2,0),(3-2,0).故可设圆C的圆心为(3,t),
则有32+(t-1)2=(2)2+t2,解得t=1. 则圆C的半径为=3.
则以圆C的方程为(x-3)2+(y-1)2=9. …………………………………6分
(2)设A(x1,y1),B(x2,y2),其坐标满足方程组:
.消去y,得到方程2x2+(2a-8)x+a2-2a+1=0.
由已知可得,判别式Δ=56-16a-4a2>0. 从而x1+x2=4-a,x1x2=.①
由于OA⊥OB,可得x1x2+y1y2=0,又y1=x1+a,y2=x2+a,
所以2x1x2+a(x1+x2)+a2=0.② 由①,②得a=-1,满足Δ>0,故a=-1
…………………………………13分
20.(本小题满分14分)
解: (1) 圆心M(-1.1).∴ 圆M方程为(x+1)2+(y-1)2=2,
∴ 直线CD方程为x+y-a=0. 21世纪教育网
∵ ⊙M与直线CD相切,
∴ 圆心M到直线CD的距离d==,化简得:a=±2(舍去负值).
∴ 直线CD的方程为x+y-2=0. ……………………………5分
(2) 直线AB方程为:x-y+2=0,圆心N.
∴ 圆心N到直线AB距离为=.
∵ 直线AB截⊙N所得弦长为4,∴ 22+()2=.∴ a=±2(舍去负值).
∴ ⊙N的标准方程为(x-)2+(y-)2=6. …………………………………5分
(3) 存在.由(2)知,圆心N到直线AB距离为(定值),且AB⊥CD始终成立,
∴ 当且仅当圆N半径=2,即a=4时,⊙N上有且只有三个点到直线AB的距离为
…………………………………14分
21. (本小题满分14分)
解:(Ⅰ)函数的定义域…1分
把代入可得,把代入可得,把代入可得
因为,
所以数列只有三项: ………4分
(Ⅱ)的定义域为,21世纪教育网
若,则,
则,所以,
所以数列是首项为,公比为的等比数列,
所以,所以,
即数列的通项公式. ………9分
(Ⅲ) 若要产生一个无穷的常数列,则在上有解,
即在上有解,则或,所以或
即当
故当;当.21世纪教育网…14分
开始
i=2,s=0
s=s+i
i=i+2
否
i1000?
是
结束
(第15题)
高二数学试题
(考试时间:120分钟 总分:150分)
第Ⅰ卷 (选择题 共50分)
一、选择题(本题共10个小题,每小题5分,共50分。在每小题给出的四个选项中,只有一项是符合题目要求的。)
1.如图所示的程序框图输出的结果是( )
(A) (B) (C) (D)
2.某校选修乒乓球课程的学生中,高一年级有30名,高二年级
有40名.现用分层抽样的方法在这70名学生中抽取一个样本,
已知在高一年级的学生中抽取了6名,则在高二年级的学生中应
抽取的人数为( )
A.6 B.8 C.10 D.12
3.将1 010 011化为八进制数为( )
A.123 B.321 C.23 D.32
4.线性回归方程必过( )21世纪教育网
A、(0,0)点 B、(,0)点 C、(0,)点 D、(,)点
5.甲、乙、丙、丁四人参加奥运会射击项目选拔赛,四人的平均成绩和方差如下表所示:
从这四个人中选择一人参加奥运会射击项目比赛,最佳人选是( )
甲 乙 丙 丁
平均环数 8.6 8.9 8.9 8.2
方差s2 3.5 3.5 2.1 5.6
A.甲 B.乙 C.丙 D.丁
6.学校为了调查学生在课外读物方面的支出情况,抽出了一个容量为n且支出在[20,60)元的样本,其频率分布直方图如图所示,其中支出在[50,60)元的同学有30人,则n的值为( )
A.90 B.100 C.900 D.1000
7.右图给出的是计算的值的一个
程序框图,其中判断框内应填入的条件是( )
A. B.
C. D.
8. 某城市2010年的空气质量状况如表所示:
污染指数 30 60 100 110 130 140
概率
n=5s=0WHILE s<14s=s+nn=n-1WENDPRINT nEND
其中污染指数时,空气质量为优;时,空气质量为良;时,空气质量为轻微污染,该城市2010年空气质量达到良或优的概率为 ( )
A. B. C. D.
9. 下列程序执行后输出的结果是 ( )
A.-1 B.0 C.2 D.1
10.某市某机构调查小学生课业负担的情况,设平均每人每天做作业时间为x(单位:分钟),按时间分下列四种情况统计:①0~30分钟②30~60分钟;③60~90分钟;④90分钟以上,有1000名小学生参加了此项调查,如图是此次调查中某一项的流程图,其输出的结果是600,则平均每天做作业时间在0~60分钟内的学生的
频率是( ) A.0.20 B.0.40 C.0.60 D.0.80
第Ⅱ卷 (非选择题 共100 分)
二、填空题(本题共5小题,每小题4分,满分20分)
11.两个整数490和910的最大公约数是 .
12.如图是某赛季甲、乙两名篮球运动员每场比赛得分的茎叶图,则
甲、乙两人比赛得分的中位数之和是__________.
13. 用秦九韶算法计算多项式在时的值时,的值为_____________
14. 采用系统抽样方法从960人中抽取32人做问卷调查,为此将他们随机编号为1,2,…,960,分组后在第一组采用简单随机抽样的方法抽到的号码为9,抽到的32人中,编号落入区间[1,450]的人做问卷A,编号落入区间[451,750]的人做问卷B,其余的人做问卷C,则抽到的人中,做问卷B的人数为_________________
15. 给出下面的程序框图,那么其循环体执行的次数是_______________________
三、解答题(本大题共6个大题,共80分,解答应写出文字说明,证明过程或演算步骤)
16. (本小题满分13分)求倾斜角是直线y=-x+1的倾斜角的,且分别满足下列条件的直线方程: (1)经过点(,-1); (2)在y轴上的截距是-5.
17.(本小题满分13分)
2012年3月2日,国家环保部发布了新修订的《环境空气质量标准》.其中规定:居民区中的PM2.5年平均浓度不得超过35微克/立方米,PM2.5的24小时平均浓度不得超过75微克/立方米. 某城市环保部门随机抽取了一居民区去年40天的PM2.5的24小时平均浓度的监测数据,数据统计如下:
组别 PM2.5(微克/立方米) 频数(天) 频 率
第一组 (0,15] 4 0.1
第二组 (15,30] 12
第三组 (30,45] 8 0.2
第四组 (45,60] 8 0.2
第五组 (60,75] 0.1
第六组 (75,90) 4 0.1
(Ⅰ)试确定的值,并写出该样本的众数和中位数(不必写出计算过程);
(Ⅱ)完成相应的频率分布直方图.
(Ⅲ)求出样本的平均数,并根据样本估计总体的思想,从PM2.5的年平均浓度考虑,判断该居民区的环境是否需要改进?说明理由.
18.(本小题满分13分)
圆C:(x-1)2+(y-2)2=25,直线l:(2m+1)x+(m+1)y-7m-4=0(m∈R).
(1)证明:不论m取什么数,直线l与圆C恒交于两点;
(2)求直线l被圆C截得的线段的最短长度,并求此时m的值.
19.(本小题满分13分)在平面直角坐标系xOy中,曲线y=x2-6x+1与坐标轴的交点都在圆C上.(1)求圆C的方程;21世纪教育网
(2)若圆C与直线x-y+a=0交于A,B两点,且OA⊥OB,求a的值.
20.(本小题满分14分)
如图,平面直角坐标系xOy中,△AOB和△COD为两等腰直角三角形,
A(-2,0),C(a,0)(a>0).△AOB和△COD的外接圆圆心分别为M,N.
(1) 若⊙M与直线CD相切,求直线CD的方程;
(2) 若直线AB截⊙N所得弦长为4,求⊙N的标准方程;
(3) 是否存在这样的⊙N,使得⊙N上有且只有三个点到直线AB的距 离为,若存在,求此时⊙N的标准方程;若不存在,说明理由.
21.(本小题满分14分)
对任意函数,可按右图构造一个数列发生器.记由数列发生器产生数列.
(Ⅰ)若定义函数,且输入,请写出数列的所有项;
(Ⅱ)若定义函数,且输入,求数列的通项公式.
(Ⅲ)若定义函数,且要产生一个无穷的常数列,试求输入的初始数据的值及相应数列的通项公式.
四地六校联考2012-2013学年上学期第四地六校联考2012-2013学年上学期第一次月考
高二数学答题卷
(考试时间:120分钟 总分:150分)
选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合要求的.
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题:本大题共5小题,每小题4分,共20分。
11.__________________ 12.________________ 13._________________
14._____________________ 15._________________
三、解答题(本大题共6小题,共80分)
16. (本小题满分13分)21世纪教育网
17. (本小题满分13分)
18.(本小题满分13分)
19.(本小题满分13分)
20.(本小题满分14分)
21.(本题满分14分)
四地六校联考2012-2013学年上学期第一次月考
高二数学参考答案及评分标准
一、选择题(每小题5分,共50分
题号 1 2 3 4 5 6 7 8 9 10
答案 C B A D C B A A D B
一、选择题(每小题5分,共50分)
二、填空题(本题共5小题,每小题4分,满分20分)
11. 70 12. 64 13. -57
14. 10 15. 49921世纪教育网
三、解答题(本大题共6个大题,共80分,解答应写出文字说明,证明过程或演算步骤)
16. (本小题满分13分)
解:∵直线的方程为y=-x+1,
∴k=-,倾斜角α=120°,
由题知所求直线的倾斜角为30°,即斜率为.…………………………………4分
(1)∵直线经过点(,-1),
∴所求直线方程为y+1=(x-),
即x-3y-6=0. …………………………………9分
(2)∵直线在y轴上的截距为-5,
∴由斜截式知所求直线方程为y=x-5,
即x-3y-15=0. …………………………………13分
17. (本小题满分13分)
解:(Ⅰ),……………………………………………………… 2分
众数为22.5微克/立方米,中位数为37.5微克/立方米.……………………4分
(Ⅱ)其频率分布直方图如图所示:
…21世纪教育网…………………………8分
(Ⅲ)样本的平均数为
……10分
因为,所以去年该居民区PM2.5年平均浓度不符合环境空气质量标准,故该居民区的环境需要改进.……………………………………… 13分
18.(本小题满分13分)
解:(1)证明:∵直线l的方程可化为(2x+y-7)m+(x+y-4)=0(m∈R).
∴l过,的交点M(3,1).
又∵M到圆心C(1,2)的距离为
d==<5,
∴点M(3,1)在圆内,
∴过点M(3,1)的直线l与圆C恒交于两点.…………………………………6分
(2)∵过点M(3,1)的所有弦中,弦心距d≤,
弦心距、半弦长和半径r构成直角三角形,
∴当d2=5时,半弦长的平方的最小值为25-5=20.
∴弦长AB的最小值|AB|min=4.
此时,kCM=-,kl=-.
∵l⊥CM,
∴·=-1,解得m=-.
∴当m=-时,取到最短弦长为4.…………………………………13分
19. (本小题满分13分)
解:(1)曲线y=x2-6x+1与y轴的交点为(0,1),与x轴的交点为(3+2,0),(3-2,0).故可设圆C的圆心为(3,t),
则有32+(t-1)2=(2)2+t2,解得t=1. 则圆C的半径为=3.
则以圆C的方程为(x-3)2+(y-1)2=9. …………………………………6分
(2)设A(x1,y1),B(x2,y2),其坐标满足方程组:
.消去y,得到方程2x2+(2a-8)x+a2-2a+1=0.
由已知可得,判别式Δ=56-16a-4a2>0. 从而x1+x2=4-a,x1x2=.①
由于OA⊥OB,可得x1x2+y1y2=0,又y1=x1+a,y2=x2+a,
所以2x1x2+a(x1+x2)+a2=0.② 由①,②得a=-1,满足Δ>0,故a=-1
…………………………………13分
20.(本小题满分14分)
解: (1) 圆心M(-1.1).∴ 圆M方程为(x+1)2+(y-1)2=2,
∴ 直线CD方程为x+y-a=0. 21世纪教育网
∵ ⊙M与直线CD相切,
∴ 圆心M到直线CD的距离d==,化简得:a=±2(舍去负值).
∴ 直线CD的方程为x+y-2=0. ……………………………5分
(2) 直线AB方程为:x-y+2=0,圆心N.
∴ 圆心N到直线AB距离为=.
∵ 直线AB截⊙N所得弦长为4,∴ 22+()2=.∴ a=±2(舍去负值).
∴ ⊙N的标准方程为(x-)2+(y-)2=6. …………………………………5分
(3) 存在.由(2)知,圆心N到直线AB距离为(定值),且AB⊥CD始终成立,
∴ 当且仅当圆N半径=2,即a=4时,⊙N上有且只有三个点到直线AB的距离为
…………………………………14分
21. (本小题满分14分)
解:(Ⅰ)函数的定义域…1分
把代入可得,把代入可得,把代入可得
因为,
所以数列只有三项: ………4分
(Ⅱ)的定义域为,21世纪教育网
若,则,
则,所以,
所以数列是首项为,公比为的等比数列,
所以,所以,
即数列的通项公式. ………9分
(Ⅲ) 若要产生一个无穷的常数列,则在上有解,
即在上有解,则或,所以或
即当
故当;当.21世纪教育网…14分
开始
i=2,s=0
s=s+i
i=i+2
否
i1000?
是
结束
(第15题)
同课章节目录
