人教版初中数学九年级上册24.1.2垂直于弦的直径 课件(共25张PPT)
文档属性
| 名称 | 人教版初中数学九年级上册24.1.2垂直于弦的直径 课件(共25张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 523.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-02 19:52:22 | ||
图片预览





文档简介
(共25张PPT)
24.1.2垂直于弦的直径
第二十四章 圆
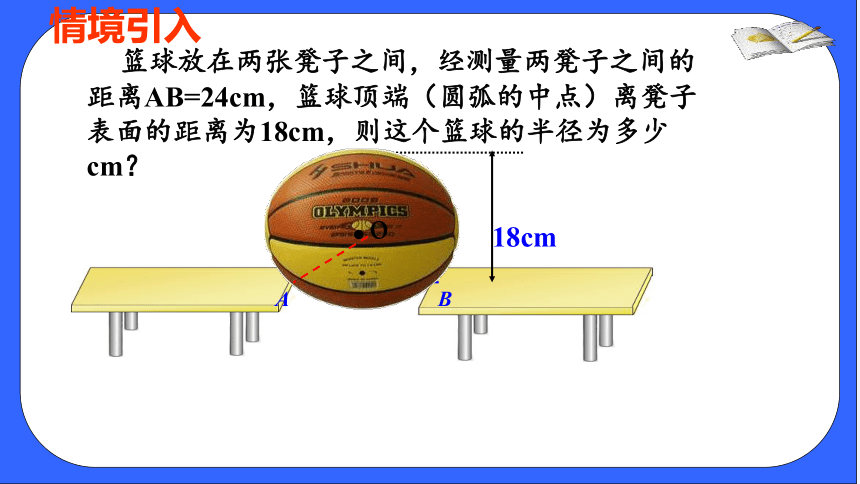
18cm
A
B
篮球放在两张凳子之间,经测量两凳子之间的距离AB=24cm,篮球顶端(圆弧的中点)离凳子表面的距离为18cm,则这个篮球的半径为多少cm?
.o
情境引入
实践探究
准备一张圆形纸片,并将这个圆形纸片沿着它的任意一条直径对折,重复几次,你发现了什么?由此你能得到什么结论?
活动一
圆是轴对称图形,任何一条直径所在直线都是它的对称轴.
理由:在△OAA1中,
∵OA=OA1,AA1⊥CD,
∴AE=A1E.
即CD是AA1的对称轴,
这就是说,对于圆上任意一点A,在圆上都有关于直线CD的对称点A1,
因此⊙O关于直线CD对称.
圆是轴对称图形证明过程:
将圆形纸片沿直径CD对折,在弧上找一组对称点A与B,连结AB,
请同学们找出图中有哪些相等的线段和弧?为什么?
实践探究
活动二
CD⊥AB于E
CD与AB有什么样的位置关系?
D
·
O
A
E
B
C
⌒
⌒
AC =BC,
⌒
⌒
AD=BD.
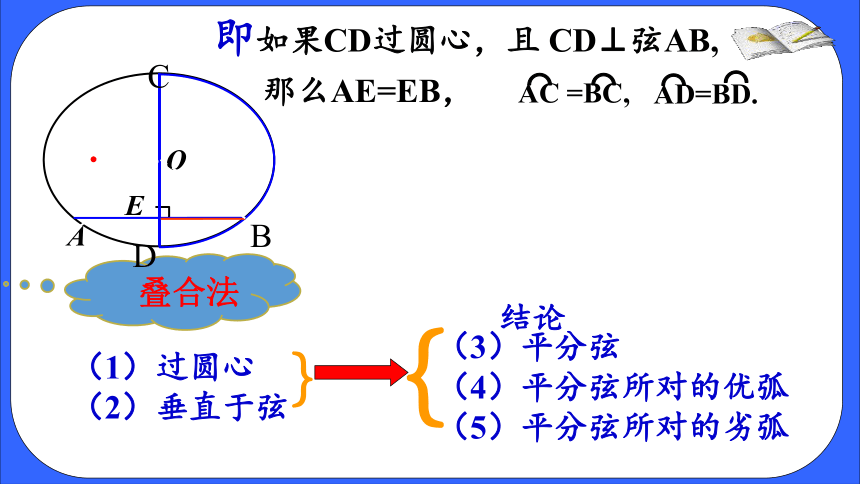
即如果CD过圆心,且 CD⊥弦AB,
那么AE=EB,
结论
(1)过圆心
(2)垂直于弦
(3)平分弦
(4)平分弦所对的优弧
(5)平分弦所对的劣弧
{
}
·
O
A
E
叠合法
B
C
D
图1
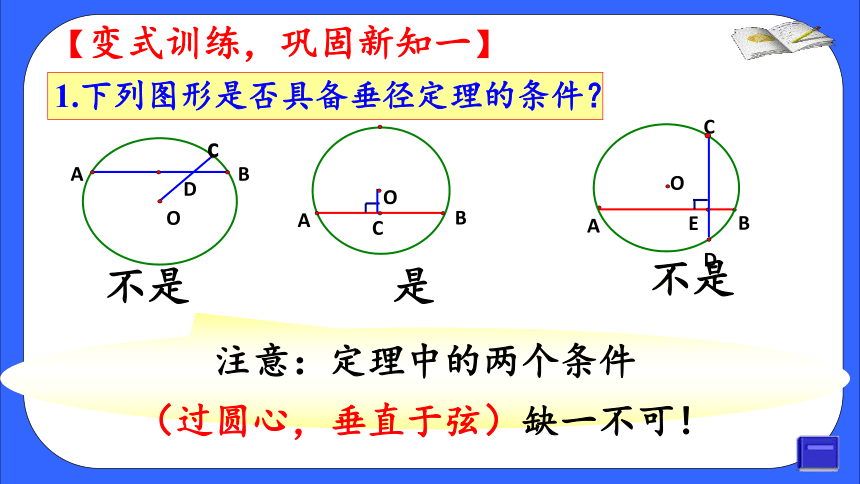
1.下列图形是否具备垂径定理的条件?
O
E
D
C
A
B
D
O
A
B
c
C
O
A
B
【变式训练,巩固新知一】
2.如图1,已知⊙O的弦AB=4,圆心O到AB的距离为1,那么⊙O的
半径为____
3.如图2,已知:如图,直径CD⊥AB,垂足为E .若半径R = 5 ,AB = 8 , 则DE 的长________
C
O
A
B
┐
1.下列图形是否具备垂径定理的条件?
是
不是
不是
O
E
D
C
A
B
注意:定理中的两个条件
(过圆心,垂直于弦)缺一不可!
D
O
A
B
c
C
O
A
B
【变式训练,巩固新知一】
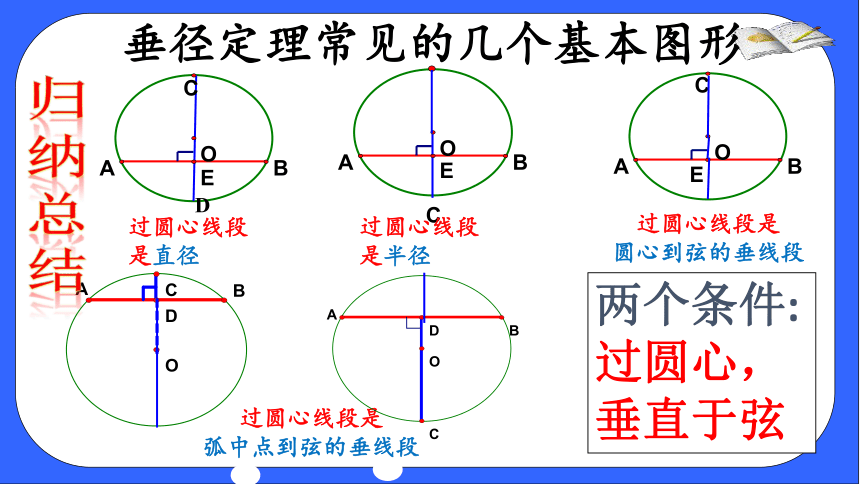
垂径定理常见的几个基本图形
E
C
O
A
B
E
C
O
A
B
D
E
C
O
A
B
过圆心线段
是直径
过圆心线段是
圆心到弦的垂线段
过圆心线段是
弧中点到弦的垂线段
两个条件:
过圆心,
垂直于弦
过圆心线段
是半径
2.如图1,已知⊙O的弦AB=4,圆心O到AB
的距离为1,那么⊙O的半径为____
3.如图2,已知:如图,直径CD⊥AB,垂足为E .
若半径R = 5 ,AB = 8 , 则DE 的长________
⊙O的弦AB=6,H为AB的中点,OH=3,则∠OAB=
C
O
A
B
图1
┐
图2
2
CD⊥AB,
⌒
⌒
AC=BC,
⌒
⌒
AD=BD.
O
A
E
B
D
C
AB与CD位置关系式是:
等量关系有:
实践探究
如果把图中的“直径CD⊥AB”改为“直径CD
平分AB”,即AE=BE那么CD还垂直AB吗?
两个结论还成立吗?请说出理由.
活动三
直径CD平分弦AB
那么CD⊥AB,
C
O
D
A
B(弦AB不是直径)
A
B(弦AB是直径)
A
B(弦AB是直径)
⌒
⌒
AC=BC,
⌒
⌒
AD=BD
如果题目中的
(AB是直径)
还成立吗?
┐
C
O
D
B(弦AB不是直径)
A
B(弦AB是直径)
A
B(弦AB是直径)
A
E
(垂径定理推论) 平分弦(不是直径)的直 径垂直于弦,并且平分弦所对的两条弧.
可推得
垂直于弦
④平分弦所对的优弧
⑤平分弦所对的劣弧
条件
结论
C
O
A
B
D
过圆心
平分弦
(弦不 是直径)
【变式训练,巩固新知二】
1.如图1,⊙O的弦AB=6,H为AB的中点,OH=3,则∠OAB= 度。
图2
C
O
A
B
图1
2.如图2,⊙O的弦AB=10,C为AB的中点,OC=3,则⊙O的半径为_____。
H
O
A
B
45
方法总结
应用垂径定理时常用到哪几个量?
它们用怎样的关系?
O
弦长a、圆半径r、
圆心到弦的距离d,
a
r
d
【变式训练,巩固新知三】1.篮球放在两张凳子之间,经测量两凳子之间距离AB=24cm,篮球顶端(圆弧的中点)
离凳子表面的距离为18cm,
篮球顶球的半径 为 多少cm?
18cm
·
A
D
C
B
O
18cm
24cm
·
A
D
C
B
O
18cm
24cm
证明:过O作OC⊥AB,并延长CO交优弧AB于点D,连接OA
∵OC⊥AB
∴AC=BC= AB,D为优
弧AB的中点
∴CD=18cm,AC=24× =12cm
设圆O的半径为R,则
AO=R,OC=18-R
∵R2=(18-R)2+122
∴R=13cm 答:篮球的半径为13cm
1、如图⊙O中,两条互相平行的弦AB、CD的长分别为10cm和24cm,已知半径为13cm,求两弦之间的距离 。
课堂练习
2、如图,⊙O的弦AB=8,M是AB的中点,且OM=3,则⊙O的半径等于( D )。
A.8 B.4 C.10 D.5
3、如图,在⊙O中,C是弧AB的中点,∠A=50 ,则∠BOC=( )。
A.40 B.45 C.50 D.60
A
4、如图,AB是⊙O的直径,弦CD⊥AB于点E,则下列结论正确的是( B )。
A.DE=BE B.BC=BD
C. BOC是等边三角形 D.四边形ODBC是菱形
课堂练习
5、银川市某居民区一处圆形下水管道破裂,修理人员准备更换一段新管道。如图所示,污水水面宽度为60cm,水面至管道顶部距离为10cm,问修理人员应准备内径多大的管道?
解:如图所示,连接OA,过O作OE⊥AB,垂足为E,交圆于F,
则AE= AB = 30cm。
令⊙O的半径为R,则OA=R,OE=OF-EF=R-10。
解得R =50cm。
修理人员应准备内径为100cm的管道。
在Rt AEO中,OA2=AE2+OE2,即R2=302+(R-10)2。
课堂练习
圆是轴对称图形,经过圆心的每一条直线都是它的对称轴.
垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.
垂径定理:
在解决有关圆的问题时,可以利用垂径定理将其转化为解直角三角形的问题 。
根据垂径定理与推论可知对于一个圆和一条直线来说。如果具备
(1)过圆心 (2)垂直于弦 (3)平分弦
(4)平分弦所对的优弧 (5)平分弦所对的劣弧
上述五个条件中的任何两个条件都可以推出其他三个结论
课堂小结
挖掘潜力
某地有一座圆弧形拱桥圆心为O,桥下水面宽度为7、2 m ,过O 作OC ⊥ AB 于D, 交圆弧于C,CD=2、4m, 现有一艘宽3m,船舱顶部为方形并高出水面(AB)2m的货船要经过拱桥,此货船能否顺利通过这座拱桥?
C
N
M
A
E
H
F
B
D
O
已知⊙O 的半径为5,⊙O 的两条平行弦AB=6, CD=8,那么AB 与CD 间的距离等________ 。
【课后思考】垂径定理推论还有其它正确形式吗?请大家课后小组讨论并完成证明过程。
拓展提高
谢 谢
24.1.2垂直于弦的直径
第二十四章 圆
18cm
A
B
篮球放在两张凳子之间,经测量两凳子之间的距离AB=24cm,篮球顶端(圆弧的中点)离凳子表面的距离为18cm,则这个篮球的半径为多少cm?
.o
情境引入
实践探究
准备一张圆形纸片,并将这个圆形纸片沿着它的任意一条直径对折,重复几次,你发现了什么?由此你能得到什么结论?
活动一
圆是轴对称图形,任何一条直径所在直线都是它的对称轴.
理由:在△OAA1中,
∵OA=OA1,AA1⊥CD,
∴AE=A1E.
即CD是AA1的对称轴,
这就是说,对于圆上任意一点A,在圆上都有关于直线CD的对称点A1,
因此⊙O关于直线CD对称.
圆是轴对称图形证明过程:
将圆形纸片沿直径CD对折,在弧上找一组对称点A与B,连结AB,
请同学们找出图中有哪些相等的线段和弧?为什么?
实践探究
活动二
CD⊥AB于E
CD与AB有什么样的位置关系?
D
·
O
A
E
B
C
⌒
⌒
AC =BC,
⌒
⌒
AD=BD.
即如果CD过圆心,且 CD⊥弦AB,
那么AE=EB,
结论
(1)过圆心
(2)垂直于弦
(3)平分弦
(4)平分弦所对的优弧
(5)平分弦所对的劣弧
{
}
·
O
A
E
叠合法
B
C
D
图1
1.下列图形是否具备垂径定理的条件?
O
E
D
C
A
B
D
O
A
B
c
C
O
A
B
【变式训练,巩固新知一】
2.如图1,已知⊙O的弦AB=4,圆心O到AB的距离为1,那么⊙O的
半径为____
3.如图2,已知:如图,直径CD⊥AB,垂足为E .若半径R = 5 ,AB = 8 , 则DE 的长________
C
O
A
B
┐
1.下列图形是否具备垂径定理的条件?
是
不是
不是
O
E
D
C
A
B
注意:定理中的两个条件
(过圆心,垂直于弦)缺一不可!
D
O
A
B
c
C
O
A
B
【变式训练,巩固新知一】
垂径定理常见的几个基本图形
E
C
O
A
B
E
C
O
A
B
D
E
C
O
A
B
过圆心线段
是直径
过圆心线段是
圆心到弦的垂线段
过圆心线段是
弧中点到弦的垂线段
两个条件:
过圆心,
垂直于弦
过圆心线段
是半径
2.如图1,已知⊙O的弦AB=4,圆心O到AB
的距离为1,那么⊙O的半径为____
3.如图2,已知:如图,直径CD⊥AB,垂足为E .
若半径R = 5 ,AB = 8 , 则DE 的长________
⊙O的弦AB=6,H为AB的中点,OH=3,则∠OAB=
C
O
A
B
图1
┐
图2
2
CD⊥AB,
⌒
⌒
AC=BC,
⌒
⌒
AD=BD.
O
A
E
B
D
C
AB与CD位置关系式是:
等量关系有:
实践探究
如果把图中的“直径CD⊥AB”改为“直径CD
平分AB”,即AE=BE那么CD还垂直AB吗?
两个结论还成立吗?请说出理由.
活动三
直径CD平分弦AB
那么CD⊥AB,
C
O
D
A
B(弦AB不是直径)
A
B(弦AB是直径)
A
B(弦AB是直径)
⌒
⌒
AC=BC,
⌒
⌒
AD=BD
如果题目中的
(AB是直径)
还成立吗?
┐
C
O
D
B(弦AB不是直径)
A
B(弦AB是直径)
A
B(弦AB是直径)
A
E
(垂径定理推论) 平分弦(不是直径)的直 径垂直于弦,并且平分弦所对的两条弧.
可推得
垂直于弦
④平分弦所对的优弧
⑤平分弦所对的劣弧
条件
结论
C
O
A
B
D
过圆心
平分弦
(弦不 是直径)
【变式训练,巩固新知二】
1.如图1,⊙O的弦AB=6,H为AB的中点,OH=3,则∠OAB= 度。
图2
C
O
A
B
图1
2.如图2,⊙O的弦AB=10,C为AB的中点,OC=3,则⊙O的半径为_____。
H
O
A
B
45
方法总结
应用垂径定理时常用到哪几个量?
它们用怎样的关系?
O
弦长a、圆半径r、
圆心到弦的距离d,
a
r
d
【变式训练,巩固新知三】1.篮球放在两张凳子之间,经测量两凳子之间距离AB=24cm,篮球顶端(圆弧的中点)
离凳子表面的距离为18cm,
篮球顶球的半径 为 多少cm?
18cm
·
A
D
C
B
O
18cm
24cm
·
A
D
C
B
O
18cm
24cm
证明:过O作OC⊥AB,并延长CO交优弧AB于点D,连接OA
∵OC⊥AB
∴AC=BC= AB,D为优
弧AB的中点
∴CD=18cm,AC=24× =12cm
设圆O的半径为R,则
AO=R,OC=18-R
∵R2=(18-R)2+122
∴R=13cm 答:篮球的半径为13cm
1、如图⊙O中,两条互相平行的弦AB、CD的长分别为10cm和24cm,已知半径为13cm,求两弦之间的距离 。
课堂练习
2、如图,⊙O的弦AB=8,M是AB的中点,且OM=3,则⊙O的半径等于( D )。
A.8 B.4 C.10 D.5
3、如图,在⊙O中,C是弧AB的中点,∠A=50 ,则∠BOC=( )。
A.40 B.45 C.50 D.60
A
4、如图,AB是⊙O的直径,弦CD⊥AB于点E,则下列结论正确的是( B )。
A.DE=BE B.BC=BD
C. BOC是等边三角形 D.四边形ODBC是菱形
课堂练习
5、银川市某居民区一处圆形下水管道破裂,修理人员准备更换一段新管道。如图所示,污水水面宽度为60cm,水面至管道顶部距离为10cm,问修理人员应准备内径多大的管道?
解:如图所示,连接OA,过O作OE⊥AB,垂足为E,交圆于F,
则AE= AB = 30cm。
令⊙O的半径为R,则OA=R,OE=OF-EF=R-10。
解得R =50cm。
修理人员应准备内径为100cm的管道。
在Rt AEO中,OA2=AE2+OE2,即R2=302+(R-10)2。
课堂练习
圆是轴对称图形,经过圆心的每一条直线都是它的对称轴.
垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.
垂径定理:
在解决有关圆的问题时,可以利用垂径定理将其转化为解直角三角形的问题 。
根据垂径定理与推论可知对于一个圆和一条直线来说。如果具备
(1)过圆心 (2)垂直于弦 (3)平分弦
(4)平分弦所对的优弧 (5)平分弦所对的劣弧
上述五个条件中的任何两个条件都可以推出其他三个结论
课堂小结
挖掘潜力
某地有一座圆弧形拱桥圆心为O,桥下水面宽度为7、2 m ,过O 作OC ⊥ AB 于D, 交圆弧于C,CD=2、4m, 现有一艘宽3m,船舱顶部为方形并高出水面(AB)2m的货船要经过拱桥,此货船能否顺利通过这座拱桥?
C
N
M
A
E
H
F
B
D
O
已知⊙O 的半径为5,⊙O 的两条平行弦AB=6, CD=8,那么AB 与CD 间的距离等________ 。
【课后思考】垂径定理推论还有其它正确形式吗?请大家课后小组讨论并完成证明过程。
拓展提高
谢 谢
同课章节目录
