华师大版九年级数学27.1.3圆周角同步练习(word版含答案)
文档属性
| 名称 | 华师大版九年级数学27.1.3圆周角同步练习(word版含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 181.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-02 00:00:00 | ||
图片预览

文档简介
华师大版九年级数学27.1.3圆周角
第1课时 圆周角定理同步练习 含答案
知识点1认识圆周角
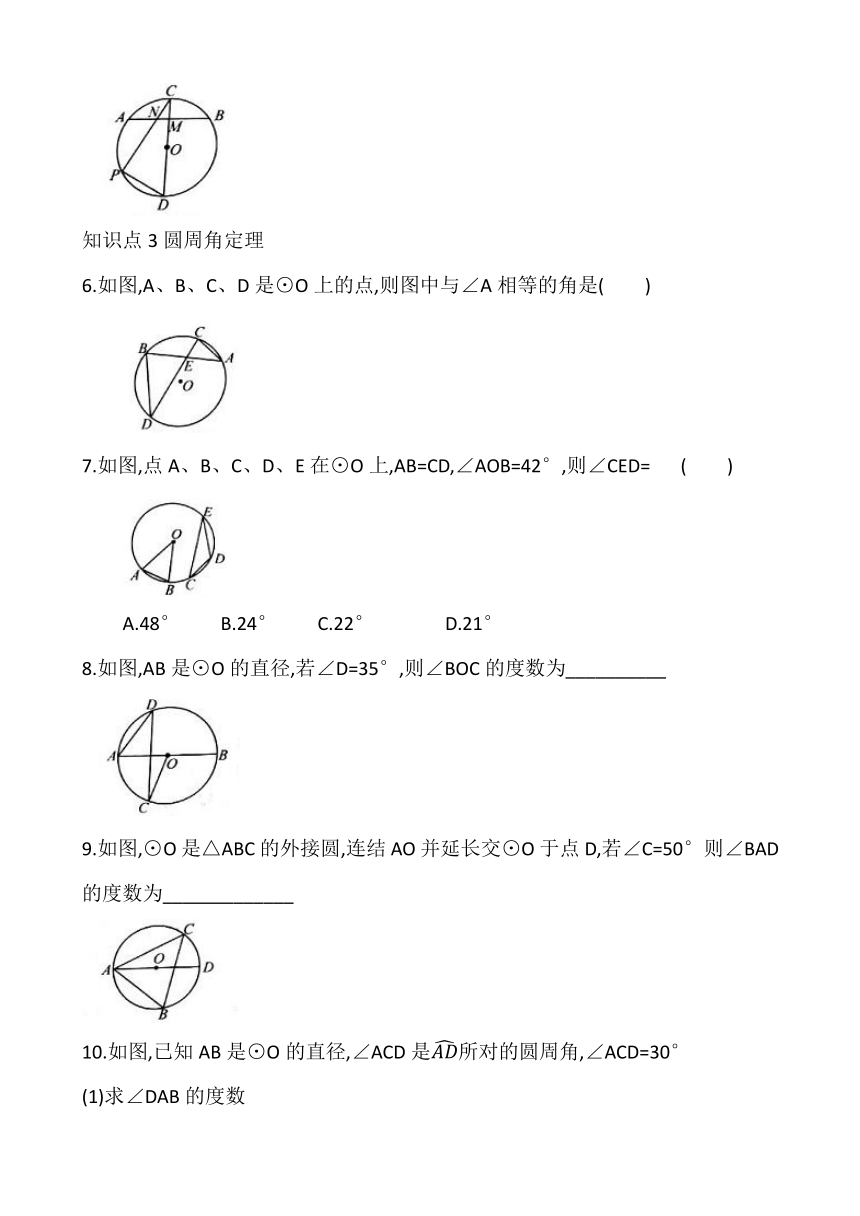
1.下面图形中的角,是圆周角的是( )
2.数一数图中有_____个圆周角,分别是_____________
知识点2半圆或直径与所对圆周角的关系
3.如图,AB是⊙O的直径,AC、BC是⊙O的弦,若∠A=20°,则∠B的度数为( )
A.70 B.90° C.40° D.60
4.如图,BC是⊙O的直径,A是⊙O上的一点,∠OAC=32°,则∠B=_______
5.如图,CD为⊙O的直径,弦AB交CD于点M,M是AB的中点,点P在上,PC与AB交于点N,若∠PNA=60°,则∠PDC=__________
知识点3圆周角定理
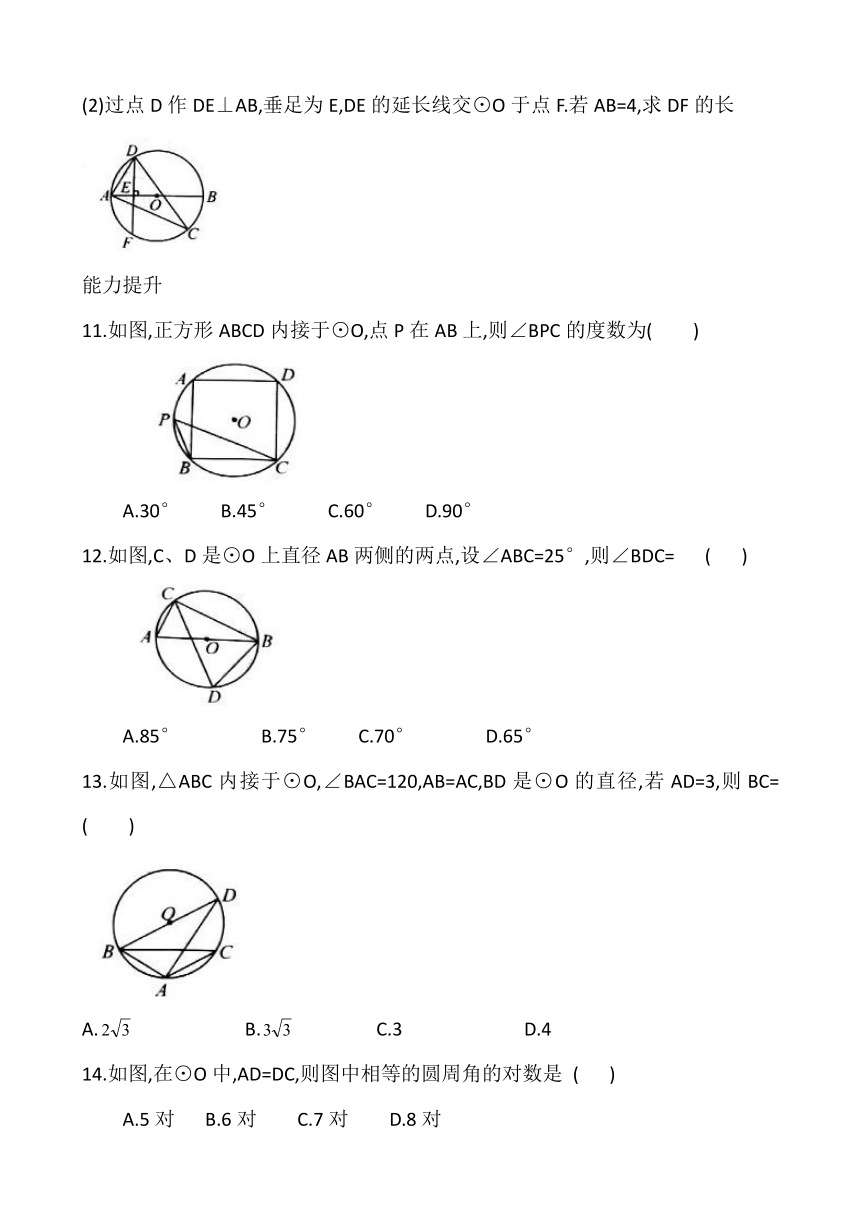
6.如图,A、B、C、D是⊙O上的点,则图中与∠A相等的角是( )
7.如图,点A、B、C、D、E在⊙O上,AB=CD,∠AOB=42°,则∠CED= ( )
A.48° B.24° C.22° D.21°
8.如图,AB是⊙O的直径,若∠D=35°,则∠BOC的度数为__________
9.如图,⊙O是△ABC的外接圆,连结AO并延长交⊙O于点D,若∠C=50°则∠BAD的度数为_____________
10.如图,已知AB是⊙O的直径,∠ACD是所对的圆周角,∠ACD=30°
(1)求∠DAB的度数
(2)过点D作DE⊥AB,垂足为E,DE的延长线交⊙O于点F.若AB=4,求DF的长
能力提升
11.如图,正方形ABCD内接于⊙O,点P在AB上,则∠BPC的度数为( )
A.30° B.45° C.60° D.90°
12.如图,C、D是⊙O上直径AB两侧的两点,设∠ABC=25°,则∠BDC= ( )
A.85° B.75° C.70° D.65°
13.如图,△ABC内接于⊙O,∠BAC=120,AB=AC,BD是⊙O的直径,若AD=3,则BC= ( )
A. B. C.3 D.4
14.如图,在⊙O中,AD=DC,则图中相等的圆周角的对数是 ( )
A.5对 B.6对 C.7对 D.8对
15.如图,⊙O的半径为1,△ABC内接于⊙O.若∠A=60°,∠B=75°,则AB=_______
16.在⊙O中,若弦BC垂直平分半径OA,则弦BC所对的圆周角等于________
17.如图,AD和AC分别是⊙O的直径和弦,且∠CAD=30°,OB⊥AD交AC于点B,若OB=3,则BC=_________
18.如图,B、C为⊙O上两定点,A为⊙O上一、动点,过点B作BE∥AC,交⊙O于点E,D为射线BC上一动点,且AC平分∠BAD,连结CE
(1)求证:AD∥EC
(2)连结EA,若BC=CD,试判断四边形EBCA的形状,并说明理由
拓展创新
19.如图,在半径为5的⊙O中,直径AB的不同侧有定点C和动点P,已知BC:CA=4:3,点P在上运动
(1)当点P与点C关于AB对称时,求CP的长
(2)当点P运动到的中点时,求CP的长
(3)当点P在上运动时,CP的长的取值范围为
答案
1.B
2.6∠A、∠B、∠C、∠BDC、∠ADB、∠ADC
3.A
4.58°
5.60°
6.D
7.D
8.110°
9.40°
10.解:(1)60°(2)
11.B
12.D
13.C
14.D
15.
16.60°或120°
17.3
18.(1)证明:∵AC平分∠BAD,∴∠BAC=∠DAC.∵∠BEC=∠BAC,∴∠BEC=∠DAC.∵BE∥AC,∴∠BEC=∠ECA∴∠ECA=∠DAC.∴AD∥EC
(2)解:四边形EBCA是矩形.理由如下:∵AD∥EC,∴∠BCE=∠D.又∵∠CEB=∠DAC,BC=CD,∴△BCE≌△CDA∴BE=CA.又∵BE∥AC,∴四边形EBCA是平行四边形∴AE∥BC.∴∠BAE=∠ABC.∵∠BAE=∠BCE,∠BCE=∠D,∴∠ABC=∠D.又∵BC=CD,∴AC⊥BD,即∠ACB=90°∴平行四边形EBCA是矩形
19.解:(1)9.6.
(2)
(3)6
第1课时 圆周角定理同步练习 含答案
知识点1认识圆周角
1.下面图形中的角,是圆周角的是( )
2.数一数图中有_____个圆周角,分别是_____________
知识点2半圆或直径与所对圆周角的关系
3.如图,AB是⊙O的直径,AC、BC是⊙O的弦,若∠A=20°,则∠B的度数为( )
A.70 B.90° C.40° D.60
4.如图,BC是⊙O的直径,A是⊙O上的一点,∠OAC=32°,则∠B=_______
5.如图,CD为⊙O的直径,弦AB交CD于点M,M是AB的中点,点P在上,PC与AB交于点N,若∠PNA=60°,则∠PDC=__________
知识点3圆周角定理
6.如图,A、B、C、D是⊙O上的点,则图中与∠A相等的角是( )
7.如图,点A、B、C、D、E在⊙O上,AB=CD,∠AOB=42°,则∠CED= ( )
A.48° B.24° C.22° D.21°
8.如图,AB是⊙O的直径,若∠D=35°,则∠BOC的度数为__________
9.如图,⊙O是△ABC的外接圆,连结AO并延长交⊙O于点D,若∠C=50°则∠BAD的度数为_____________
10.如图,已知AB是⊙O的直径,∠ACD是所对的圆周角,∠ACD=30°
(1)求∠DAB的度数
(2)过点D作DE⊥AB,垂足为E,DE的延长线交⊙O于点F.若AB=4,求DF的长
能力提升
11.如图,正方形ABCD内接于⊙O,点P在AB上,则∠BPC的度数为( )
A.30° B.45° C.60° D.90°
12.如图,C、D是⊙O上直径AB两侧的两点,设∠ABC=25°,则∠BDC= ( )
A.85° B.75° C.70° D.65°
13.如图,△ABC内接于⊙O,∠BAC=120,AB=AC,BD是⊙O的直径,若AD=3,则BC= ( )
A. B. C.3 D.4
14.如图,在⊙O中,AD=DC,则图中相等的圆周角的对数是 ( )
A.5对 B.6对 C.7对 D.8对
15.如图,⊙O的半径为1,△ABC内接于⊙O.若∠A=60°,∠B=75°,则AB=_______
16.在⊙O中,若弦BC垂直平分半径OA,则弦BC所对的圆周角等于________
17.如图,AD和AC分别是⊙O的直径和弦,且∠CAD=30°,OB⊥AD交AC于点B,若OB=3,则BC=_________
18.如图,B、C为⊙O上两定点,A为⊙O上一、动点,过点B作BE∥AC,交⊙O于点E,D为射线BC上一动点,且AC平分∠BAD,连结CE
(1)求证:AD∥EC
(2)连结EA,若BC=CD,试判断四边形EBCA的形状,并说明理由
拓展创新
19.如图,在半径为5的⊙O中,直径AB的不同侧有定点C和动点P,已知BC:CA=4:3,点P在上运动
(1)当点P与点C关于AB对称时,求CP的长
(2)当点P运动到的中点时,求CP的长
(3)当点P在上运动时,CP的长的取值范围为
答案
1.B
2.6∠A、∠B、∠C、∠BDC、∠ADB、∠ADC
3.A
4.58°
5.60°
6.D
7.D
8.110°
9.40°
10.解:(1)60°(2)
11.B
12.D
13.C
14.D
15.
16.60°或120°
17.3
18.(1)证明:∵AC平分∠BAD,∴∠BAC=∠DAC.∵∠BEC=∠BAC,∴∠BEC=∠DAC.∵BE∥AC,∴∠BEC=∠ECA∴∠ECA=∠DAC.∴AD∥EC
(2)解:四边形EBCA是矩形.理由如下:∵AD∥EC,∴∠BCE=∠D.又∵∠CEB=∠DAC,BC=CD,∴△BCE≌△CDA∴BE=CA.又∵BE∥AC,∴四边形EBCA是平行四边形∴AE∥BC.∴∠BAE=∠ABC.∵∠BAE=∠BCE,∠BCE=∠D,∴∠ABC=∠D.又∵BC=CD,∴AC⊥BD,即∠ACB=90°∴平行四边形EBCA是矩形
19.解:(1)9.6.
(2)
(3)6
