2021-2022学年高一上学期数学人教A版(2019)必修第一册4.2指数函数 学案
文档属性
| 名称 | 2021-2022学年高一上学期数学人教A版(2019)必修第一册4.2指数函数 学案 |
|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-04 20:56:18 | ||
图片预览




文档简介
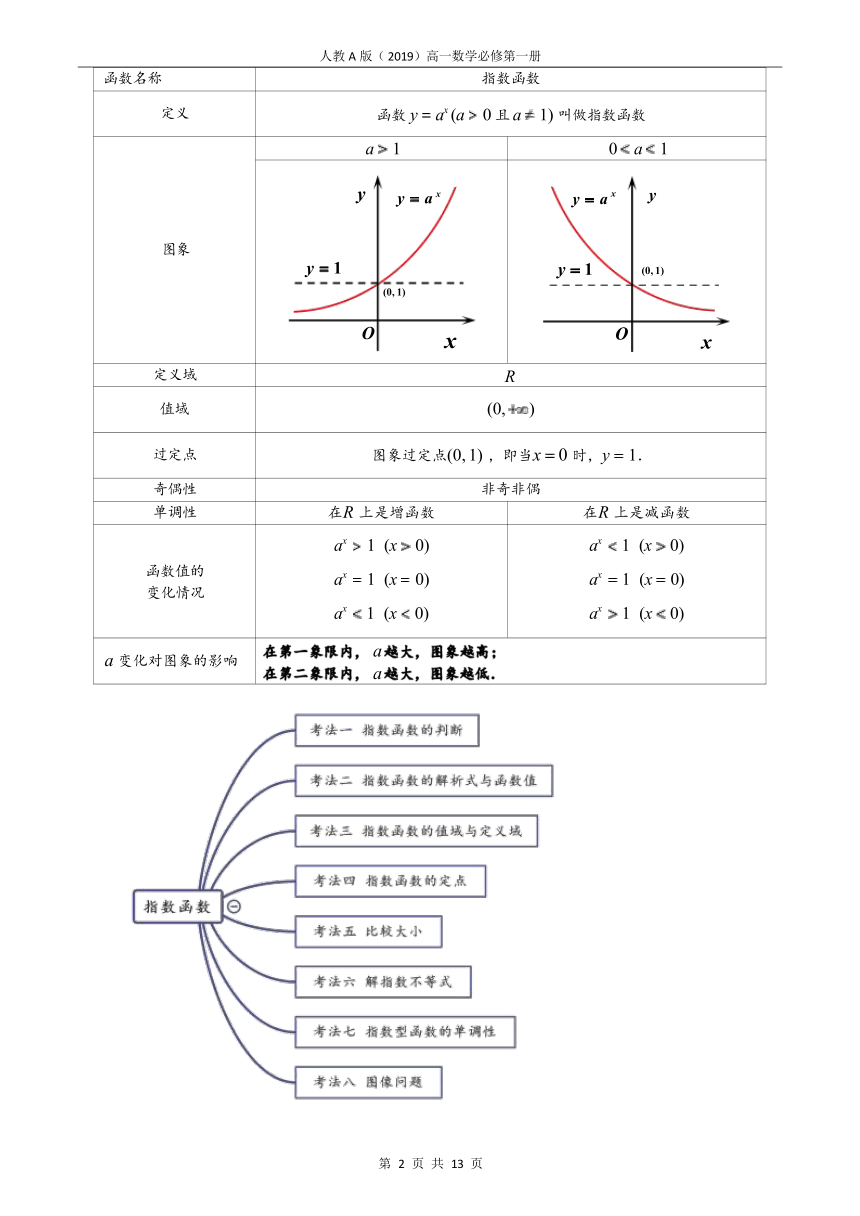
4.2 指数函数
1. 了解指数函数的概念. 2.会画出指数函数图象. 3.掌握并能应用指数函数的性质.
人教 A 版( 2019)高一数学必修第一册
第 1 页 共 13 页
人教 A 版( 2019)高一数学必修第一册
函数名称 指数函数
定义 函数 y ax (a 0 且 a 1) 叫做指数函数
图象 a 1 0 a 1
(
y
y
a
x
y
1
(0,
1)
O
x
) (
x
) O
定义域 R
值域 (0, )
过定点 图象过定点(0, 1) ,即当x 0 时,y 1.
奇偶性 非奇非偶
单调性 在R 上是增函数 在R 上是减函数
函数值的 变化情况 ax 1 (x 0) ax 1 (x 0) ax 1 (x 0) ax 1 (x 0) ax 1 (x 0) ax 1 (x 0)
a 变化对图象的影响 在第一象限内, a 越大,图象越高; 在第二象限内, a 越大,图象越低.
(
x
y
y
1
(0,
1)
y
a
)
第 2 页 共 13 页
(
2
b
0,
b
2.
) (
1
) (
3
) (
1
) (
1
) (
3
) (
8
,
8
2
) (
1
1
1
) (
8
,
) (
1
)人教 A 版( 2019)高一数学必修第一册
第 3 页 共 13 页
【题型 1 指数函数的判断】
【例 1】 ( 1) 2021 ·上海高一 专题练习) 下列是指数函数的是 ( )
A.y 3x B.y 2x2 1
C.y ax D.y x
(2)若函数y k 2 ax 2 b (a 0 , 且a 1)是指数函数,则k ______, b ______.
【答案】(1) D(2) -1 2
【解析】(1) 根据指数函数的特征:系数为 1,底数
满足 a 0 且 a 1 , 自变量在指数位置可知,A,
B,C不满足,D 满足.故选: D.
(
(2)
,
解得
,
)k 2 1 k 1
【题型2 指数函数的解析式与函数值】
【例 2】(1) 若指数函数 f(x)的图象经 过点(2,9),则 f(-1)=________. (2)(2021 ·全国) 已知函数f(x) 2x , 则f f(2) = ___.
1
【答案】(1) ( 2) 16
3
【解析】(1) 设 f(x)=xa(a>0,且 a≠1),将点(2,
9)代入,得a2=9,解得 a=3 或 a=-3 (舍去).
所以 f(x)=3x.所以 f(-1)=3-1 = .(2) 根据题
3
意,函数f(x) 2x ,则f 2 22 4 ,则
f f(2) f 4 24 16 ,故答案为: 16.
【练习 1-1】 (多选)下列各函数中,是指数函数的是( )
A.y= (-3)x B.y=3x C. D.y=(1) x
【答案】 BD【解析】 指数函数的一般形式为: y ax (a 0,a 1)
选项 A 中, 3 0 ,所以选项 A 错误; 根据指数函数的定义,选型 BD 正确;
选项 C 中, y 3x 1 ·3x ,不符合指数函数的形式,选项 C 错误; 故选: BD. 3
【练习 1-2】若函数y a2 3a 3 ax 是指数函数,则a ____. a2 3a 3 1,
【解】 由题意可得 a 0, 解得 a 2 .故答案为: 2.
a 1,
【练习 1-3】 下列函数中是指数函数的是________ (填序号).
① y 2 x ;② y 2x 1 ;③ y
【答案】③【解析】①中指数式 x 的系数不为 1 ,故不是指数函数;
②中 y 2x 1 2x ,指数式 2x 的系数不为 1 ,故不是指数函数; 2
③是指数函数.故答案为: ③
【练习 2-1】指数函数 y ax 的图象经过点 3, 则a=( )
1 1
A . B . C . 2 D . 4 4 2
【答案】B【解析】因为 y ax 的图象经过点 3, 所以 a3 ,解得 a ,
【练习 2-2】(2021 ·太原市第五十六中学校高一月考) 若指数
函数f x 的图象经过点(2, 9) ,则f(x) __________, f( 1) ___________.
1
【答案】 3x
3
【解析】设f x ax ( a 0 且 a 1),因为 f x 的图象经过点 (2, 9) ,
所以 a2 9 ,可得 a 3 ,所以 f x 3x ,所以 f 1 3 1 1 ,
(
2
4
2
4
) (
3
3
1
1
) (
3
3
) (
1
3
x
3
x
1
3
x
1
1
) (
3
x
) (
3
3
) (
1
3
x
1
3
x
1
3
x
) (
1
3
x
1
3
x
1
3
x
) (
10
)人教 A 版( 2019)高一数学必修第一册
第 4 页 共 13 页
【题型 3 指数函数的值域与定义域】
【例 3】 求下列函数的定义域和值域:
(1) (3) (
1
2
x
) (
3
) (
2
.
)y 2x 2 ; ( 2)y ; y
【解析】 (1)∵x应满足x-2≠0, ∴x≠2, ∴定义
域为{x|x≠2,x∈R}.
∵ 0 , ∴ y 2 1 , ∴ y 2 的
值域为{y|y>0,且 y≠1}.
(2)定义域为 R. ∵|x|≥0, ∴
2 x 3x 30 1 , ∴此函数的
值域为[1,+∞).
(3)由题意知1 1 x 0 , ∴ 1x 1 10
∴x≥0, ∴定义域为{x|x≥0,x∈R}.
∵x≥0, ∴ 0 1 x 1 ∴ 0 1 1 x 1,
∴0≤y<1, ∴此函数的值域为[0,1).
【练习 3-1】 函数y 的定义域为( )
A.( , 3) B.(, 3] C.(3, ) D.[3, )
【答案】 D【解析】 由题意得2x 8 0 ,所以 2x 23 ,解得 x 3 .故选: D.
【练习 3-2】(多选) 若指数函数y ax 在区间[ 1, 1] 上的最大值
和最小值的和为 ,则a 的值可能是( )
3
1 1
A . B . C . 3 D . 2 2 3
【答案】 BC【解析】 当 a 1时,函数 y ax 在区间[ 1, 1]上为单调递增函数,
当 x 1 时, ymax a ,当 x 1 时, ymin a 1 ,
所以 a a 1 10 ,即3a2 10a 3 0 ,解得 a 3 或 a 1 ,
因为 a 1 ,所以 a 3 ;
当 0 a 1时,函数 y ax 在区间[ 1, 1]上为单调递减函数,
当 x 1 时, ymin a ,当 x 1 时, ymax a 1 ,
所以 a a 1 10 ,即3a2 10a 3 0 ,解得 a 3 或 a 1 ,
因为 0 a 1 ,所以 a .综上可得,实数 a 的值为 3 或 .
【练习 3-3】 若函数 f(x)= 的定义域是[1,+∞),则 a
的取值范围是( )
A.[0,1) ∪ (1,+∞) B. (1,+∞)
C. (0,1) D. (2,+∞)
【答案】 B【解析】 ∵xa-a≥0, ∴xa≥a, ∴当a>1 时,x≥1.故函数定义域为[1,
+∞)时,a>1.
【练习 3-4】 函数 y= 的定义域____; 值域_________ .
【解】 函数的定义域为 R. ∵y= = =1- ,又∵3x>0, ∴1
1 1 1
+3x>1,∴0< <1,∴- 1<- <0,∴0<1- <1,∴值域为(0,1).
【练习 3-5】 函数y 4x 4 x 2x 2 x 的最小值为( )
1 7
A . B . 1 C . 2 D . 2 4
【答案】 D【解】 令 2x 2 x t ,则 t2 4x 4 x 2 ,则
y t2 t 2 t 1 2 7 ,当t 1 时,可得最小值为 7 .
(
y
x
) (
2
2
) (
2
)人教 A 版( 2019)高一数学必修第一册
第 5 页 共 13 页
【题型 4 指数函数的定点】
【例 4】( 1)(2021 ·上海高一专题练习) 函数y ax2020 2022(a 0,a 1) 的图 像恒过定点______. (2)(2021 ·高邮市临泽中学高一月考) 已知函数f (x) a x2 3(a 0 且a 1) 的图象恒过定点 A,若点 A在一次函数
y mx n 的图象上,其中实数m,n满
足mn 0,则 1 2 的最小值为______.
m n
【答案】(1) 2020, 2023 (2) 4
【解】(1) a0 1(a 0, a 1) ,令
x 2020 0 ,得x 2020,
y a0 2022 2023,
(2) 由题意可得 A 2, 2 , ∵点 A 在一次函
数y mx n 的图象上, ∴2m n 2 , ∵ m,n 0 ,所以
(
1
2
1
(
1
2
)
2
m
n
1
(4
n
4
m
)
1
(4
2
)
4
)m n 2 m n 2 m n 2 m n
1
,当且仅当 m , n 1时取得等号;
2
【题型 5 比较大小】
【例 5】(2021 ·江西高安中学高一月考)
已知a 31. 1 ,b 41. 1 ,c 30.9 ,则a ,b ,
c 的大小关系为( )
A.c a b B.c b a
C.b a c D.b c a
【答案】A【解】由题意,构造函数 y 3x , y x 1.1 ,
两个函数在(0, )单调递增; 由
0.9 1.1 30.9 31.1 c a ;由
3 4 31.1 41.1 a b ;综上: c a b
练习 4-1】 已知函数f(x) ax 1 xa 2 ( a 0 且a 1 )的图象
恒过定点P ,则点P 的坐标为____________.
【答案】 1, 4【解】x 1 时,f(1) 1 1 2 4 ,所以函数图象恒过定点 (1, 4) .
【练习 4-2】(2021 ·上海市建平中学高一期末)对于任意实数a ,
函数f(x) ax3 1 ( a 0 且a 1)的图像经过一个定点,则
该定点的坐标是________.
【答案】 3, 3 【解析】 因为函数f(x) ax3 1 图像可以通过 y ax 向
左平移 3 个单位得 y ax3 ,再将 y ax3 图像上的点向上平移 个单位得到, 且指数函数 y ax ( a 0 且 a 1)恒过定点(0, 1) ,
【练习 4-3】(2021 ·上海市民办西南高级中学高一月考) 函数
y ax 1 1 a 0, a 1 的图象恒过定点_______.
【答案】 1, 2
【解析】 当 x 1 时,y a0 1 2 , y ax 1 1 a 0, a 1 的图象恒 过定点 1, 2 .
练习 5-1】 已知a ,b 20.8 ,c 40.2 ,则a, b, c 的大小关系 为( )
A.c b a B.c a b C.b a c D.b c a
【答案】 B
【解析】 a 20.5 ,c 40.2 20.4 ,∵ y 2x 递增,且 0.4 0.5 0.8, ∴ 20.4 20.5 20.8 ,即c a b .
(
4
2
1
)【练习 5-2】 已知a 23 ,b 45 ,c 253 , A.a b c B.a c b C.b a c 【答案】 C 4 1 2 1 1 【解析】 a 23 163 ,b 45 165 , c 253 , 则( ). D.c a b
1
且幂函数 3 在R上单调递增,指数函数 y 16x 在 R上单调递增,则
b a c ,故选: C.
(
4
) (
4
,
) (
A.
,
) (
8
) (
C.
,
) (
A.
,
2
B.
,
2
) (
a
,即不等式的解集为
) (
8
.
) (
1
) (
B.必要不充分条件
D.既不充分也不必要条件
) (
3
x
3
x
,
) (
3
x
3
x
) (
3
x
3
x
,
3
x
3
x
3
2
x
1
2
) (
3
x
3
x
) (
3
x
3
x
3
2
x
1
3
2
x
1
)人教 A 版( 2019)高一数学必修第一册
第 6 页 共 13 页
【题型 6 解指数不等式】
【例 6】(1) 已知不等式2x2 1 1 x 2
则函数y 2x 的值域是( )
1 1
8 8
1 D. 2,
(
x
,
x
0
)(2) 已知函数f(x) e xx 0 ,若
f(a 1) f(a) ,则实数 a的取值范围
是( )
1 B. 1 ,
(
2
2
1
1
) (
2
2
)C. 0, D. , 1
【答案】(1) B(2) A
【解】(1) 由题可得 2x2 1 1 x 2 22 x 2 ,
因为 y 2x 在 R 上单调递增,所以
x2 1 2x 4 即 x2 2x 3 0 ,解得: 3 x 1 ,所以 23 y 2x 21 ,即函数
y 2x 的值域是 , 2
(
x
,
x
0
)(2) 因为 f(x) e xx 0 ,当 x 0 时
f(x) e x 单调递减,且f(x) 1,当 x 0 时, f(x) x3 单调递减,且f(x) 0 ,所以函数
(
x
,
x
0
)f(x) e xx 0 在定义域上单调递减,因为
f(a 1) f(a) ,所以 a 1 a ,解得
1 1
2 , 2
【练习 6-1】 若0.3x 0.3y 1 ,则( ) A.x y 0 B.y x 0 C.x y 0 D.y x 0
【答案】 C
【解析】令f t 0.3t , ∵ 0 0.3 1, ∴f t 为 R 上的单调递减函数, 由已知得: f x f y 1 f 0 , ∴ x y 0 ,故选: C.
【练习 6-2】(2021 ·辽宁高一月考)设p : 22x 1 128 ,q : 3 x 4 ,
则p 是q 的( )
A.充分不必要条件
C.充要条件
【答案】 B
【解析】 22x 1 128 27 , 2x 1 7 ,即 x 4 .
x 4 不能够推出 3 x 4 ,而 3 x 4能够推出 x 4 , 命题p 是命题q
的必要不充分条件.故选: B
【练习 6-3】 函数 f(x)= 2 若有 f(a)+f(a-2)
>4,则 a的取值范围是________.
【答案】(1,+∞)
【解析】 设 F(x)=f(x)-2,则 F(x)= 易知 F(x)是奇函数,F
(x)= = =1- 在 R上是增函数,
由 f(a)+f(a-2) >4 得 F(a)+F(a-2) >0,
于是可得 F(a)>F(2-a),即a>2-a,解得 a>1.答案:( 1,+∞)
(
2
) (
C.
a
0,
D.
a
,
2
) (
3
.
) (
1
) (
1
2
) (
B.必要不充分条件
D.既不充分也不必要条件
) (
1
)人教 A 版( 2019)高一数学必修第一册
第 7 页 共 13 页
【题型 7 指数型函数的单调性】
【例 7】(1) 函数 y= 1x2-2 的单调递 2
减区间为( )
A.(- ∞ ,0] B.[0,+∞)
C.(- ∞ , ] D. [ ,+∞)
(2)(2021 ·江苏高一课时练习) 函数
(
a
2
x
3
a
,
x
0
)f(x) ax , x 0 ,满足对任
意x1 x2 , f x1 f x2
(
都有
0
成立,
x
x
)1 2
则a 的取值范围是( )
(
A.
a
0,
1
1
) (
3
)B.a , 1
1 1
3 3
【答案】(1) B(2) C
【解析】(1) 数 y= ( 1) u在 R上为减函数,
欲求函数y= 1x2 2 的单调递减区间,只需求函 2
数u=x2-2 的单调递增区间,
而函数u=x2-2 的单调递增区间为[0,+∞),故所
求单调递减区间为[0,+∞) .故选:B
(2) f (x)满足对任意 x1 x2 ,都有
f(x1) f(x2) 0 成立,
x x
f(x)在 R上是减函数,
0 a 1
a 2 0 ,解得 0 a 1 , a (a 2) 0 3a a0 3
的取值范围是 0, 故选: C .
【练习 7-1】“ a 3 ”是“函数f(x) (a 1)x 在R上为增函数”
的( )
A.充分不必要条件
C.充要条件
【答案】 A
【解析】若f x 在R上为增函数,则 a 1 1 ,即 a 2 ,
因为 a 3是 a 2 的充分不必要条件,
所以“ a 3 ”是“函数f(x) (a 1)x 在 R上为增函数”的充分不必要条件.
(
4
ax
a
,
x
0
)【练习 7-2】 已知函数f x ax 2a, x 0 ,其中a 0 ,且
a 1 ,若f x 在R 上单调,则a 的取值范围是( )
(
3
3
2
2
) (
1
1
1
1
)A. 0, B. , 1 C. 0, D. , 1
【答案】 B
(
4
ax
a
,
x
0
)【解析】 函数 f x ax 2a, x 0 ,其中 a 0 ,且 a 1,
因为函数f x 在 R上单调,又因为函数 y 4ax a 在 , 0 上为减函数, 所以函数f x 在 R上为减函数,则函数 y ax 2a 在0, 上为减函数,
可得 0 a 1 ,且有 a0 2a a ,解得 a .
(
3
1
) (
3
.
)综上可知,实数 a 的取值范围是 , 1
【练习 7-3】(2021 ·汕头市达濠华侨中学高一期末) 已知函数
f x 2x2 2x ,则f x 的单调递增区间是______.
【答案】 1,
【解析】 函数f x 2x2 2x 是由 y 2t和t x2 2x 复合而成,
因为y 2t为单调递增函数,
t x2 2x 对称轴为x 1 ,开口向上,
所以t x2 2x 在 , 1 上单调递减,在 1, 上单调递增,
所以f 所以f x 2x2 2x 在 , 1 上单调递减,在 1, 上单调递增, x 2x2 2x 的单调递增区间为 1, ,
(
1
x
1
x
) (
2
) (
已知
y
1
y
2
3
x
,
) (
3
,
) (
2
) (
2
) (
1
) (
1
1
1
) (
1
1
) (
B.
a
>1,
b
>0
D.0<
a
<1,
b
<0
)人教 A 版( 2019)高一数学必修第一册
第 8 页 共 13 页
【题型 8 图像问题】
【例 8】(1) 1x
y3 10 x ,y4 10x ,则在同一平面直角
坐标系内,它们的图象大致为( )
A. B.
C. D.
(2)(2021 ·河北安平中学) 函数
f x 2x a R 的图象不可能为
( )
(
C
) A. . (
D
) B. .
【答案】(1) A(2) C
【解析】(1) y2 3x 与 y4 10x 是增函数,
y1 3 与 y3 10 x 10 是减函数,在
第一象限内作直线x 1 ,
该直线与四条曲线交点的纵坐标的大小对应各底数的大小,易知: 选 A.故选: A
(2) 当 a 0 时, f x 2x ,图象 A 满足;
当 a 1时,f x 2x ,f 0 2 ,且f x f x ,此时函数是
偶函数,关于 y 轴对称,图象 B 满足;
当 a 1 时, f x 2x , f 0 0 ,且 f x f x ,此时函
数是奇函数,关于原点对称,图象 D 满足; 图象 C 过点0, 1 ,此时 a 0 ,故 C
不成立.故选: C.
【练习 8-1】(多选)函数y ax (a>0,a≠1)图象可能是( )
a
A. B. 【答案】 CD (
C.
D.
)
【解析】 当a>1 时, ∈(0,1),因此x=0 时,0a a a
上单调递增,故 C 符合; 当 01,因此x=0 时,y<0,且y=xa- 在
a a
R上单调递减,故 D 符合.
【练习 8-2】(2021 年广东) 已知 0②y=的图象为( )
【答案】 C
【解析】 由于 0=1 与两个曲线相交,交点在下面的是函数y=xm的图象.
3.(2021 年河北) 函数 f(x)=-b的图象如图所示,其中a,b
为常数,则下列结论正确的是( )
A.a>1,b<0
C.00
【答案】 D
【解析】 从曲线的变化趋势,可以得到函数 f(x)为减函数,从而有 0位置看,是由函数y=xa(00,
即b<0.
(
1
1
2
) (
2
x
1
) (
1
1
1
2
1
1
1
) (
4
1
x
) (
2
1
2
1
) (
2
x
1
)
人教 A 版( 2019)高一数学必修第一册
第 9 页 共 13 页
一、选择题
1 .已知a 33 ,b 95 ,c 59 ,
A .a b c B . a c b
【基础训练】
则 a ,b ,c 的大小关系是( )
C .c a b D .c b a
【答案】 C
【详解】 ∵ a 33 96 95 b , c 59 259 279 33 a , ∴ c a b .
2 .设 a 30.4 , b 50.4 ,
A .b a c B.
【答案】 A
c 0.45 ,则( b c a
)
C .c a b D . a c b
【详解】 因为函数f x x0.4 在0, 上的增函数,且 3 < 5 ,
所以 30.4 50.4 ,即 a b 又 a 30.4 1,c 0.45 1 ,所以 a c ,所以 b a c .
3 .函数y 1 的定义域为( )
A .[2, 1) B . ( , 1) C .(2, 1)
【答案】 A
(
【详解】
由题意,
1
x
4
0
,得
x
1
,所以
-
2
x
<
1
.
)2x 1 0 x 2
4 .若 0.3x 0.3y 1 ,则( ) A .x y 0 B . y x 0 C .x y 0
D . (1, 2)
D .y x 0
【答案】 C【详解】令f t 0.3t , ∵ 0 0.3 1, ∴ f t 为 R 上的单调递减函数,
由已知得: f x f y 1 f 0 , ∴ x y 0 ,
5 .已知函数f(x) 2 ax 1a R ,则f 2021 f 2021 ( )
A . 2a 2021
C .4
B .2a
D .4042
【答案】 C【详解】 因为 f(x) 2 ax 1a R ,
所以 f 2021 f 2021 2021a 1 2021a 1
(
1
) (
A
.
) (
B
.
) (
.
) (
.
) (
2
) (
A
.
,
) (
2
) (
2
) (
1
) (
2
,
) (
2
) (
C
) (
D
)
6 .函数f x ax 2 的图像恒过定点P ,则P 的坐标是( )
人教 A 版( 2019)高一数学必修第一册
第 10 页 共 13 页
A . 0, 1
【答案】 D【详解】
1 1
7 .22 、33 、
B . 1, 0 C . 1, 2 D . 0, 3
由指数函数 y ax 恒过定点0, 1 ,所以函数 f x ax 2 的图像恒过定点 P 0, 3 .
66 这三个数的大小关系为( )
A. 1 1 1 66 33 22 B. 1 1 1 66 22 33 (
.
) (
C
)
【答案】 B
1 3 1 2
【解】 22 26 , 33 36 ,
8 .函数y ax 1 (a 0, a 1) 的图象可能是( a
1 1 1
22 33 66
1
66 ,因为
)
(
6
6
)
(
D
). 1 1 1 33 22 66
,所以 6 2 3 .
【答案】 D
【解】 若 0 a 1 ,则 1 1 , y ax 1 (a 0, a 1) 在 y ax 的基础上向下平移 1 个单位长度,故 C 错,D 对;
a a a
若 a 1 ,则 0 1 1 , y ax 1 (a 0, a 1) 在 y ax 的基础上向下平移 1 个单位长度,故 A ,B 错;
a a a
ax , x 1
8 .若函数f(x) = 4 a x 2 x 1是 R 上的增函数,则实数 a 的取值范围为( )
A .(1 ,+∞)
【答案】 D【详解】
B .(1,8)
(
,
)a 1
由题意得 4 a 0,
C .(4,8) D .[4,8)
解得 4≤a<8.
a (4 a ) 1 2,
9 .若函数f x 3 2a1 x3 在R 上是减函数,则实数 a 的取值范围是( )
1
2
B . 1 ,
C . 1 , 2 1,
(
2
)D . , 1
【答案】 A
【详解】令 u 2a 1 x 3 ,由于函数f x 3 2a1 x3 在 R 上是减函数,外层函数 y 3u 3为 R 上的增函数,则
(
2
) (
2
) (
2
) (
2
) (
值域
0,
) (
D
.
0
恒成立
) (
1
2
) (
2
)内层函数 u 2a 1 x 3 为 R 上的减函数,所以, 2a 1 0 ,解得 a 1 .
10 .函数 y f (x) 是 R 上的奇函数,当x 0 时,f(x) 2x ,则当x 0 时, f(x) ( )
A . ﹣ 2x B .2 ﹣ x C . ﹣ 2 ﹣ x D .2x
【答案】 C
【详解】 解: 当 x 0 时, f(x) 2x ,当 x 0 时, x 0 ,则 f(x) 2 x .
又 f(x) 是 R 上的奇函数,所以当 x 0时 f(x) f(x) 2 x .
11 .如图所示: 曲线C1 , C2 , C3 和C4 分别是指数函数y ax ,y bx , y cx 和y dx 的图象,
人教 A 版( 2019)高一数学必修第一册
第 11 页 共 13 页
则 a ,b ,c ,d 与 1 的大小关系是( )
A .a b 1 c d B .a b 1 d c
C .b a 1 c d D .b a 1 d c
【答案】 D
【详解】 因为当底数大于 1 时,指数函数是定义域上的增函数,
当底数小于 1 时,指数函数是定义域上的减函数,
所以 c ,d 大于 1 ,a ,b 小于 1,
由图知: c1 d1 ,即 c d , b1 a1 ,即 b a ,所以 b a 1 d c ,
12 .(多选) 对函数f(x) 1x2 1 判断正确的是( )
A .增区间 (0, ) B .增区间 ( , 0) C .值域 1 , D.
【答案】 BD
【详解】 根据指数函数性质, f x = 1x 在 , 单调递减,
而 f x x2 1 在 ,0 单调递减,在 0, 单调递增,
故 f(x) 1 x2 1 增区间为 ,0 ; f x x2 1 值域为 1, ,
而 f(x) x2 1 在 , 单调递减,故 f(x) x2 1 值域为 0, .
1
2
13 .(多选) 已知函数f x ,则下面几个结论正确的有( )
A .f x 的图象关于原点对称
C . f x 的值域为 1, 1
B .f x 的图象关于y 轴对称
x1 , x2 R ,且x1 x2 , f x1 f x2
x x
(
2
) (
x
x
) (
1
2
1
2
1
t
) (
3
3
) (
1
2
1
2
1
2
,
) (
1
2
1
2
) (
2
) (
2
x
1
2
·
x
) (
1
2
2
2
1
2
) (
2
x
1
2
)【答案】 AD
【详解】 对于 A , f(x) 则 f(x) f(x)
则f(x) 为奇函数,故图象关于原点对称,故 A 正确.
对于 B ,计算f(1) 1 , f( 1) 1 f(1) ,故f(x) 的图象不关于y 轴对称,故 B 错误.
对于 C , f(x) 1 , 1 2x t, t (1, ) ,
故 y f(x) 1 ,易知: 1 ( 1, 1) ,故 f(x) 的值域为 ( 1, 1) ,故 C 错误.
对 D , f(x) 1 2 x ,因为 y 1 2x 在 R 上为增函数, y 1 2 为 (1, ) 上的减函数,
由复合函数的单调性可得f x 在 R 上单调递减,故x1 , x2 R ,且 x1 x2 , f(x1) f(x2 ) 0 恒成立,故 D 正确.
1 2
二、解答题
14 .已知函数f(x)= 1 1 3.
(1)求f(x)的定义域; (2)判断f(x)的奇偶性; (3)求证: f(x)>0.
【详解】(1)由 2x -1≠0 ,得 x≠0.所以函数的定义域为(-∞ ,0)∪(0 ,+∞).
(2)因为函数f(x)的定义域关于原点对称,
f(-x)= ( 1) (x)3
= ( 1 ) x3 ( 1 ) x3 f (x),
所以f(x)为偶函数.
(3)证明: 当 x>0 时, 1 0 ,x3>0 ,所以f(x)>0. 2x 1
因为f(x)为偶函数,所以当 x<0 时,f(x)>0.
综上所述,对于定义域内的任意 x 都有f(x)>0.
15 .已知函数 f(x) ax 2 (a 0, a 1, x 0) 的图像经过点 (3, 0.5) ,
(1)求 a 值; (2)求函数 f(x) ax 2 (x 0) 的值域;
1
【详解】(1)由题意可得 a3 2 0.5 ,解得 a .
2
(2)由(1)可知 f(x) ( 1)x 2 (x 0) ,
因为 0 1 1 ,所以 f x 在[0, ) 上单调递减,
则 f x 在 x 0 时有最大值,所以 f xmax f(0) ()2 4 ,
因为 f x 0 ,所以函数 f x 的值域为 (0, 4] .
第 12 页 共 13 页
人教 A 版( 2019)高一数学必修第一册
(
a
2
9
a
9,
a
) (
3
2
4
) (
4
) (
3
a
4
) (
2
3
) (
5
) (
4
4
11
) (
3
a
4
) (
2
4
) (
3
) (
5
) (
a
3
a
1,
a
)【提升训练】
16 .设函数 f(x) (a 1)a x b(a 0, a 1) ,则函数 f(x) 的单调性( )
人教 A 版( 2019)高一数学必修第一册
第 13 页 共 13 页
A .与 a 有关,且与 b 有关
C .与 a 有关,且与 b 无关
B .与 a 无关,且与 b 有关
D .与 a 无关,且与 b 无关
【答案】 D
【详解】 当 0 a 1时, f(x) (a 1)a x b 单调递增.
当 a 1时, f(x) (a 1)a x b 单调递增.
则 a 0且 a 1 , b R , f(x) (a 1)a x b 的单调性都为单调递增.
所以函数f(x) (a 1)a x b 的单调性与 a,b 无关.
17 .已知函数f(x )=9x ﹣ a 3x+1+a2(x ∈[0 ,1] ,a ∈R),记f(x )的最大值为 g(a). (Ⅰ)求 g(a )解析式;
(Ⅱ)若对于任意 t∈[ ﹣ 2 ,2] ,任意 a ∈R ,不等式 g(a )≥ ﹣ m2+tm 恒成立,求实数 m 的范围.
【解】(Ⅰ)令 u=3x ∈[1 ,3] ,则f(x )=h(u)=u2 ﹣ 3au+a2.
当 ≤2 ,即 a≤ 时,g(a)=h(u)max =h (3)=a2 ﹣ 9a+9;
2 3
当 2 ,即 a> 时,g(a)=h (u)max=h( 1)=a2 ﹣ 3a+1;
4
故 g(a )= ;
3
(Ⅱ)当 a≤ 时,g(a)=a2 ﹣ 9a+9,g(a )min=g( )= ﹣ ;
3 3 9
当 a 时,g(a)=a2 ﹣ 3a+1 ,g(a)min=g( 3 )= ﹣ 5 ;
3 5
因此 g(a)min=g( )= ﹣ ;
2 4
对于任意任意 a ∈R ,不等式 g(a )≥ ﹣m2+tm 恒成立等价于 ﹣ m2+tm≤ ﹣ .
4
令 h (t)=mt ﹣ m2 ,由于 h (t)是关于 t 的一次函数,
故对于任意 t∈[ ﹣ 2 ,2]都有 h(t)≤ ﹣
4
(
h
(2)
5
4
m
8
m
5
0
2
2
)则 h(2) ,即 4m 8m 5 0 ,解得 m≤ ﹣ 5 或 m≥ 5 .
4
1. 了解指数函数的概念. 2.会画出指数函数图象. 3.掌握并能应用指数函数的性质.
人教 A 版( 2019)高一数学必修第一册
第 1 页 共 13 页
人教 A 版( 2019)高一数学必修第一册
函数名称 指数函数
定义 函数 y ax (a 0 且 a 1) 叫做指数函数
图象 a 1 0 a 1
(
y
y
a
x
y
1
(0,
1)
O
x
) (
x
) O
定义域 R
值域 (0, )
过定点 图象过定点(0, 1) ,即当x 0 时,y 1.
奇偶性 非奇非偶
单调性 在R 上是增函数 在R 上是减函数
函数值的 变化情况 ax 1 (x 0) ax 1 (x 0) ax 1 (x 0) ax 1 (x 0) ax 1 (x 0) ax 1 (x 0)
a 变化对图象的影响 在第一象限内, a 越大,图象越高; 在第二象限内, a 越大,图象越低.
(
x
y
y
1
(0,
1)
y
a
)
第 2 页 共 13 页
(
2
b
0,
b
2.
) (
1
) (
3
) (
1
) (
1
) (
3
) (
8
,
8
2
) (
1
1
1
) (
8
,
) (
1
)人教 A 版( 2019)高一数学必修第一册
第 3 页 共 13 页
【题型 1 指数函数的判断】
【例 1】 ( 1) 2021 ·上海高一 专题练习) 下列是指数函数的是 ( )
A.y 3x B.y 2x2 1
C.y ax D.y x
(2)若函数y k 2 ax 2 b (a 0 , 且a 1)是指数函数,则k ______, b ______.
【答案】(1) D(2) -1 2
【解析】(1) 根据指数函数的特征:系数为 1,底数
满足 a 0 且 a 1 , 自变量在指数位置可知,A,
B,C不满足,D 满足.故选: D.
(
(2)
,
解得
,
)k 2 1 k 1
【题型2 指数函数的解析式与函数值】
【例 2】(1) 若指数函数 f(x)的图象经 过点(2,9),则 f(-1)=________. (2)(2021 ·全国) 已知函数f(x) 2x , 则f f(2) = ___.
1
【答案】(1) ( 2) 16
3
【解析】(1) 设 f(x)=xa(a>0,且 a≠1),将点(2,
9)代入,得a2=9,解得 a=3 或 a=-3 (舍去).
所以 f(x)=3x.所以 f(-1)=3-1 = .(2) 根据题
3
意,函数f(x) 2x ,则f 2 22 4 ,则
f f(2) f 4 24 16 ,故答案为: 16.
【练习 1-1】 (多选)下列各函数中,是指数函数的是( )
A.y= (-3)x B.y=3x C. D.y=(1) x
【答案】 BD【解析】 指数函数的一般形式为: y ax (a 0,a 1)
选项 A 中, 3 0 ,所以选项 A 错误; 根据指数函数的定义,选型 BD 正确;
选项 C 中, y 3x 1 ·3x ,不符合指数函数的形式,选项 C 错误; 故选: BD. 3
【练习 1-2】若函数y a2 3a 3 ax 是指数函数,则a ____. a2 3a 3 1,
【解】 由题意可得 a 0, 解得 a 2 .故答案为: 2.
a 1,
【练习 1-3】 下列函数中是指数函数的是________ (填序号).
① y 2 x ;② y 2x 1 ;③ y
【答案】③【解析】①中指数式 x 的系数不为 1 ,故不是指数函数;
②中 y 2x 1 2x ,指数式 2x 的系数不为 1 ,故不是指数函数; 2
③是指数函数.故答案为: ③
【练习 2-1】指数函数 y ax 的图象经过点 3, 则a=( )
1 1
A . B . C . 2 D . 4 4 2
【答案】B【解析】因为 y ax 的图象经过点 3, 所以 a3 ,解得 a ,
【练习 2-2】(2021 ·太原市第五十六中学校高一月考) 若指数
函数f x 的图象经过点(2, 9) ,则f(x) __________, f( 1) ___________.
1
【答案】 3x
3
【解析】设f x ax ( a 0 且 a 1),因为 f x 的图象经过点 (2, 9) ,
所以 a2 9 ,可得 a 3 ,所以 f x 3x ,所以 f 1 3 1 1 ,
(
2
4
2
4
) (
3
3
1
1
) (
3
3
) (
1
3
x
3
x
1
3
x
1
1
) (
3
x
) (
3
3
) (
1
3
x
1
3
x
1
3
x
) (
1
3
x
1
3
x
1
3
x
) (
10
)人教 A 版( 2019)高一数学必修第一册
第 4 页 共 13 页
【题型 3 指数函数的值域与定义域】
【例 3】 求下列函数的定义域和值域:
(1) (3) (
1
2
x
) (
3
) (
2
.
)y 2x 2 ; ( 2)y ; y
【解析】 (1)∵x应满足x-2≠0, ∴x≠2, ∴定义
域为{x|x≠2,x∈R}.
∵ 0 , ∴ y 2 1 , ∴ y 2 的
值域为{y|y>0,且 y≠1}.
(2)定义域为 R. ∵|x|≥0, ∴
2 x 3x 30 1 , ∴此函数的
值域为[1,+∞).
(3)由题意知1 1 x 0 , ∴ 1x 1 10
∴x≥0, ∴定义域为{x|x≥0,x∈R}.
∵x≥0, ∴ 0 1 x 1 ∴ 0 1 1 x 1,
∴0≤y<1, ∴此函数的值域为[0,1).
【练习 3-1】 函数y 的定义域为( )
A.( , 3) B.(, 3] C.(3, ) D.[3, )
【答案】 D【解析】 由题意得2x 8 0 ,所以 2x 23 ,解得 x 3 .故选: D.
【练习 3-2】(多选) 若指数函数y ax 在区间[ 1, 1] 上的最大值
和最小值的和为 ,则a 的值可能是( )
3
1 1
A . B . C . 3 D . 2 2 3
【答案】 BC【解析】 当 a 1时,函数 y ax 在区间[ 1, 1]上为单调递增函数,
当 x 1 时, ymax a ,当 x 1 时, ymin a 1 ,
所以 a a 1 10 ,即3a2 10a 3 0 ,解得 a 3 或 a 1 ,
因为 a 1 ,所以 a 3 ;
当 0 a 1时,函数 y ax 在区间[ 1, 1]上为单调递减函数,
当 x 1 时, ymin a ,当 x 1 时, ymax a 1 ,
所以 a a 1 10 ,即3a2 10a 3 0 ,解得 a 3 或 a 1 ,
因为 0 a 1 ,所以 a .综上可得,实数 a 的值为 3 或 .
【练习 3-3】 若函数 f(x)= 的定义域是[1,+∞),则 a
的取值范围是( )
A.[0,1) ∪ (1,+∞) B. (1,+∞)
C. (0,1) D. (2,+∞)
【答案】 B【解析】 ∵xa-a≥0, ∴xa≥a, ∴当a>1 时,x≥1.故函数定义域为[1,
+∞)时,a>1.
【练习 3-4】 函数 y= 的定义域____; 值域_________ .
【解】 函数的定义域为 R. ∵y= = =1- ,又∵3x>0, ∴1
1 1 1
+3x>1,∴0< <1,∴- 1<- <0,∴0<1- <1,∴值域为(0,1).
【练习 3-5】 函数y 4x 4 x 2x 2 x 的最小值为( )
1 7
A . B . 1 C . 2 D . 2 4
【答案】 D【解】 令 2x 2 x t ,则 t2 4x 4 x 2 ,则
y t2 t 2 t 1 2 7 ,当t 1 时,可得最小值为 7 .
(
y
x
) (
2
2
) (
2
)人教 A 版( 2019)高一数学必修第一册
第 5 页 共 13 页
【题型 4 指数函数的定点】
【例 4】( 1)(2021 ·上海高一专题练习) 函数y ax2020 2022(a 0,a 1) 的图 像恒过定点______. (2)(2021 ·高邮市临泽中学高一月考) 已知函数f (x) a x2 3(a 0 且a 1) 的图象恒过定点 A,若点 A在一次函数
y mx n 的图象上,其中实数m,n满
足mn 0,则 1 2 的最小值为______.
m n
【答案】(1) 2020, 2023 (2) 4
【解】(1) a0 1(a 0, a 1) ,令
x 2020 0 ,得x 2020,
y a0 2022 2023,
(2) 由题意可得 A 2, 2 , ∵点 A 在一次函
数y mx n 的图象上, ∴2m n 2 , ∵ m,n 0 ,所以
(
1
2
1
(
1
2
)
2
m
n
1
(4
n
4
m
)
1
(4
2
)
4
)m n 2 m n 2 m n 2 m n
1
,当且仅当 m , n 1时取得等号;
2
【题型 5 比较大小】
【例 5】(2021 ·江西高安中学高一月考)
已知a 31. 1 ,b 41. 1 ,c 30.9 ,则a ,b ,
c 的大小关系为( )
A.c a b B.c b a
C.b a c D.b c a
【答案】A【解】由题意,构造函数 y 3x , y x 1.1 ,
两个函数在(0, )单调递增; 由
0.9 1.1 30.9 31.1 c a ;由
3 4 31.1 41.1 a b ;综上: c a b
练习 4-1】 已知函数f(x) ax 1 xa 2 ( a 0 且a 1 )的图象
恒过定点P ,则点P 的坐标为____________.
【答案】 1, 4【解】x 1 时,f(1) 1 1 2 4 ,所以函数图象恒过定点 (1, 4) .
【练习 4-2】(2021 ·上海市建平中学高一期末)对于任意实数a ,
函数f(x) ax3 1 ( a 0 且a 1)的图像经过一个定点,则
该定点的坐标是________.
【答案】 3, 3 【解析】 因为函数f(x) ax3 1 图像可以通过 y ax 向
左平移 3 个单位得 y ax3 ,再将 y ax3 图像上的点向上平移 个单位得到, 且指数函数 y ax ( a 0 且 a 1)恒过定点(0, 1) ,
【练习 4-3】(2021 ·上海市民办西南高级中学高一月考) 函数
y ax 1 1 a 0, a 1 的图象恒过定点_______.
【答案】 1, 2
【解析】 当 x 1 时,y a0 1 2 , y ax 1 1 a 0, a 1 的图象恒 过定点 1, 2 .
练习 5-1】 已知a ,b 20.8 ,c 40.2 ,则a, b, c 的大小关系 为( )
A.c b a B.c a b C.b a c D.b c a
【答案】 B
【解析】 a 20.5 ,c 40.2 20.4 ,∵ y 2x 递增,且 0.4 0.5 0.8, ∴ 20.4 20.5 20.8 ,即c a b .
(
4
2
1
)【练习 5-2】 已知a 23 ,b 45 ,c 253 , A.a b c B.a c b C.b a c 【答案】 C 4 1 2 1 1 【解析】 a 23 163 ,b 45 165 , c 253 , 则( ). D.c a b
1
且幂函数 3 在R上单调递增,指数函数 y 16x 在 R上单调递增,则
b a c ,故选: C.
(
4
) (
4
,
) (
A.
,
) (
8
) (
C.
,
) (
A.
,
2
B.
,
2
) (
a
,即不等式的解集为
) (
8
.
) (
1
) (
B.必要不充分条件
D.既不充分也不必要条件
) (
3
x
3
x
,
) (
3
x
3
x
) (
3
x
3
x
,
3
x
3
x
3
2
x
1
2
) (
3
x
3
x
) (
3
x
3
x
3
2
x
1
3
2
x
1
)人教 A 版( 2019)高一数学必修第一册
第 6 页 共 13 页
【题型 6 解指数不等式】
【例 6】(1) 已知不等式2x2 1 1 x 2
则函数y 2x 的值域是( )
1 1
8 8
1 D. 2,
(
x
,
x
0
)(2) 已知函数f(x) e xx 0 ,若
f(a 1) f(a) ,则实数 a的取值范围
是( )
1 B. 1 ,
(
2
2
1
1
) (
2
2
)C. 0, D. , 1
【答案】(1) B(2) A
【解】(1) 由题可得 2x2 1 1 x 2 22 x 2 ,
因为 y 2x 在 R 上单调递增,所以
x2 1 2x 4 即 x2 2x 3 0 ,解得: 3 x 1 ,所以 23 y 2x 21 ,即函数
y 2x 的值域是 , 2
(
x
,
x
0
)(2) 因为 f(x) e xx 0 ,当 x 0 时
f(x) e x 单调递减,且f(x) 1,当 x 0 时, f(x) x3 单调递减,且f(x) 0 ,所以函数
(
x
,
x
0
)f(x) e xx 0 在定义域上单调递减,因为
f(a 1) f(a) ,所以 a 1 a ,解得
1 1
2 , 2
【练习 6-1】 若0.3x 0.3y 1 ,则( ) A.x y 0 B.y x 0 C.x y 0 D.y x 0
【答案】 C
【解析】令f t 0.3t , ∵ 0 0.3 1, ∴f t 为 R 上的单调递减函数, 由已知得: f x f y 1 f 0 , ∴ x y 0 ,故选: C.
【练习 6-2】(2021 ·辽宁高一月考)设p : 22x 1 128 ,q : 3 x 4 ,
则p 是q 的( )
A.充分不必要条件
C.充要条件
【答案】 B
【解析】 22x 1 128 27 , 2x 1 7 ,即 x 4 .
x 4 不能够推出 3 x 4 ,而 3 x 4能够推出 x 4 , 命题p 是命题q
的必要不充分条件.故选: B
【练习 6-3】 函数 f(x)= 2 若有 f(a)+f(a-2)
>4,则 a的取值范围是________.
【答案】(1,+∞)
【解析】 设 F(x)=f(x)-2,则 F(x)= 易知 F(x)是奇函数,F
(x)= = =1- 在 R上是增函数,
由 f(a)+f(a-2) >4 得 F(a)+F(a-2) >0,
于是可得 F(a)>F(2-a),即a>2-a,解得 a>1.答案:( 1,+∞)
(
2
) (
C.
a
0,
D.
a
,
2
) (
3
.
) (
1
) (
1
2
) (
B.必要不充分条件
D.既不充分也不必要条件
) (
1
)人教 A 版( 2019)高一数学必修第一册
第 7 页 共 13 页
【题型 7 指数型函数的单调性】
【例 7】(1) 函数 y= 1x2-2 的单调递 2
减区间为( )
A.(- ∞ ,0] B.[0,+∞)
C.(- ∞ , ] D. [ ,+∞)
(2)(2021 ·江苏高一课时练习) 函数
(
a
2
x
3
a
,
x
0
)f(x) ax , x 0 ,满足对任
意x1 x2 , f x1 f x2
(
都有
0
成立,
x
x
)1 2
则a 的取值范围是( )
(
A.
a
0,
1
1
) (
3
)B.a , 1
1 1
3 3
【答案】(1) B(2) C
【解析】(1) 数 y= ( 1) u在 R上为减函数,
欲求函数y= 1x2 2 的单调递减区间,只需求函 2
数u=x2-2 的单调递增区间,
而函数u=x2-2 的单调递增区间为[0,+∞),故所
求单调递减区间为[0,+∞) .故选:B
(2) f (x)满足对任意 x1 x2 ,都有
f(x1) f(x2) 0 成立,
x x
f(x)在 R上是减函数,
0 a 1
a 2 0 ,解得 0 a 1 , a (a 2) 0 3a a0 3
的取值范围是 0, 故选: C .
【练习 7-1】“ a 3 ”是“函数f(x) (a 1)x 在R上为增函数”
的( )
A.充分不必要条件
C.充要条件
【答案】 A
【解析】若f x 在R上为增函数,则 a 1 1 ,即 a 2 ,
因为 a 3是 a 2 的充分不必要条件,
所以“ a 3 ”是“函数f(x) (a 1)x 在 R上为增函数”的充分不必要条件.
(
4
ax
a
,
x
0
)【练习 7-2】 已知函数f x ax 2a, x 0 ,其中a 0 ,且
a 1 ,若f x 在R 上单调,则a 的取值范围是( )
(
3
3
2
2
) (
1
1
1
1
)A. 0, B. , 1 C. 0, D. , 1
【答案】 B
(
4
ax
a
,
x
0
)【解析】 函数 f x ax 2a, x 0 ,其中 a 0 ,且 a 1,
因为函数f x 在 R上单调,又因为函数 y 4ax a 在 , 0 上为减函数, 所以函数f x 在 R上为减函数,则函数 y ax 2a 在0, 上为减函数,
可得 0 a 1 ,且有 a0 2a a ,解得 a .
(
3
1
) (
3
.
)综上可知,实数 a 的取值范围是 , 1
【练习 7-3】(2021 ·汕头市达濠华侨中学高一期末) 已知函数
f x 2x2 2x ,则f x 的单调递增区间是______.
【答案】 1,
【解析】 函数f x 2x2 2x 是由 y 2t和t x2 2x 复合而成,
因为y 2t为单调递增函数,
t x2 2x 对称轴为x 1 ,开口向上,
所以t x2 2x 在 , 1 上单调递减,在 1, 上单调递增,
所以f 所以f x 2x2 2x 在 , 1 上单调递减,在 1, 上单调递增, x 2x2 2x 的单调递增区间为 1, ,
(
1
x
1
x
) (
2
) (
已知
y
1
y
2
3
x
,
) (
3
,
) (
2
) (
2
) (
1
) (
1
1
1
) (
1
1
) (
B.
a
>1,
b
>0
D.0<
a
<1,
b
<0
)人教 A 版( 2019)高一数学必修第一册
第 8 页 共 13 页
【题型 8 图像问题】
【例 8】(1) 1x
y3 10 x ,y4 10x ,则在同一平面直角
坐标系内,它们的图象大致为( )
A. B.
C. D.
(2)(2021 ·河北安平中学) 函数
f x 2x a R 的图象不可能为
( )
(
C
) A. . (
D
) B. .
【答案】(1) A(2) C
【解析】(1) y2 3x 与 y4 10x 是增函数,
y1 3 与 y3 10 x 10 是减函数,在
第一象限内作直线x 1 ,
该直线与四条曲线交点的纵坐标的大小对应各底数的大小,易知: 选 A.故选: A
(2) 当 a 0 时, f x 2x ,图象 A 满足;
当 a 1时,f x 2x ,f 0 2 ,且f x f x ,此时函数是
偶函数,关于 y 轴对称,图象 B 满足;
当 a 1 时, f x 2x , f 0 0 ,且 f x f x ,此时函
数是奇函数,关于原点对称,图象 D 满足; 图象 C 过点0, 1 ,此时 a 0 ,故 C
不成立.故选: C.
【练习 8-1】(多选)函数y ax (a>0,a≠1)图象可能是( )
a
A. B. 【答案】 CD (
C.
D.
)
【解析】 当a>1 时, ∈(0,1),因此x=0 时,0
上单调递增,故 C 符合; 当 0
a a
R上单调递减,故 D 符合.
【练习 8-2】(2021 年广东) 已知 0
【答案】 C
【解析】 由于 0
3.(2021 年河北) 函数 f(x)=-b的图象如图所示,其中a,b
为常数,则下列结论正确的是( )
A.a>1,b<0
C.0
【答案】 D
【解析】 从曲线的变化趋势,可以得到函数 f(x)为减函数,从而有 0
即b<0.
(
1
1
2
) (
2
x
1
) (
1
1
1
2
1
1
1
) (
4
1
x
) (
2
1
2
1
) (
2
x
1
)
人教 A 版( 2019)高一数学必修第一册
第 9 页 共 13 页
一、选择题
1 .已知a 33 ,b 95 ,c 59 ,
A .a b c B . a c b
【基础训练】
则 a ,b ,c 的大小关系是( )
C .c a b D .c b a
【答案】 C
【详解】 ∵ a 33 96 95 b , c 59 259 279 33 a , ∴ c a b .
2 .设 a 30.4 , b 50.4 ,
A .b a c B.
【答案】 A
c 0.45 ,则( b c a
)
C .c a b D . a c b
【详解】 因为函数f x x0.4 在0, 上的增函数,且 3 < 5 ,
所以 30.4 50.4 ,即 a b 又 a 30.4 1,c 0.45 1 ,所以 a c ,所以 b a c .
3 .函数y 1 的定义域为( )
A .[2, 1) B . ( , 1) C .(2, 1)
【答案】 A
(
【详解】
由题意,
1
x
4
0
,得
x
1
,所以
-
2
x
<
1
.
)2x 1 0 x 2
4 .若 0.3x 0.3y 1 ,则( ) A .x y 0 B . y x 0 C .x y 0
D . (1, 2)
D .y x 0
【答案】 C【详解】令f t 0.3t , ∵ 0 0.3 1, ∴ f t 为 R 上的单调递减函数,
由已知得: f x f y 1 f 0 , ∴ x y 0 ,
5 .已知函数f(x) 2 ax 1a R ,则f 2021 f 2021 ( )
A . 2a 2021
C .4
B .2a
D .4042
【答案】 C【详解】 因为 f(x) 2 ax 1a R ,
所以 f 2021 f 2021 2021a 1 2021a 1
(
1
) (
A
.
) (
B
.
) (
.
) (
.
) (
2
) (
A
.
,
) (
2
) (
2
) (
1
) (
2
,
) (
2
) (
C
) (
D
)
6 .函数f x ax 2 的图像恒过定点P ,则P 的坐标是( )
人教 A 版( 2019)高一数学必修第一册
第 10 页 共 13 页
A . 0, 1
【答案】 D【详解】
1 1
7 .22 、33 、
B . 1, 0 C . 1, 2 D . 0, 3
由指数函数 y ax 恒过定点0, 1 ,所以函数 f x ax 2 的图像恒过定点 P 0, 3 .
66 这三个数的大小关系为( )
A. 1 1 1 66 33 22 B. 1 1 1 66 22 33 (
.
) (
C
)
【答案】 B
1 3 1 2
【解】 22 26 , 33 36 ,
8 .函数y ax 1 (a 0, a 1) 的图象可能是( a
1 1 1
22 33 66
1
66 ,因为
)
(
6
6
)
(
D
). 1 1 1 33 22 66
,所以 6 2 3 .
【答案】 D
【解】 若 0 a 1 ,则 1 1 , y ax 1 (a 0, a 1) 在 y ax 的基础上向下平移 1 个单位长度,故 C 错,D 对;
a a a
若 a 1 ,则 0 1 1 , y ax 1 (a 0, a 1) 在 y ax 的基础上向下平移 1 个单位长度,故 A ,B 错;
a a a
ax , x 1
8 .若函数f(x) = 4 a x 2 x 1是 R 上的增函数,则实数 a 的取值范围为( )
A .(1 ,+∞)
【答案】 D【详解】
B .(1,8)
(
,
)a 1
由题意得 4 a 0,
C .(4,8) D .[4,8)
解得 4≤a<8.
a (4 a ) 1 2,
9 .若函数f x 3 2a1 x3 在R 上是减函数,则实数 a 的取值范围是( )
1
2
B . 1 ,
C . 1 , 2 1,
(
2
)D . , 1
【答案】 A
【详解】令 u 2a 1 x 3 ,由于函数f x 3 2a1 x3 在 R 上是减函数,外层函数 y 3u 3为 R 上的增函数,则
(
2
) (
2
) (
2
) (
2
) (
值域
0,
) (
D
.
0
恒成立
) (
1
2
) (
2
)内层函数 u 2a 1 x 3 为 R 上的减函数,所以, 2a 1 0 ,解得 a 1 .
10 .函数 y f (x) 是 R 上的奇函数,当x 0 时,f(x) 2x ,则当x 0 时, f(x) ( )
A . ﹣ 2x B .2 ﹣ x C . ﹣ 2 ﹣ x D .2x
【答案】 C
【详解】 解: 当 x 0 时, f(x) 2x ,当 x 0 时, x 0 ,则 f(x) 2 x .
又 f(x) 是 R 上的奇函数,所以当 x 0时 f(x) f(x) 2 x .
11 .如图所示: 曲线C1 , C2 , C3 和C4 分别是指数函数y ax ,y bx , y cx 和y dx 的图象,
人教 A 版( 2019)高一数学必修第一册
第 11 页 共 13 页
则 a ,b ,c ,d 与 1 的大小关系是( )
A .a b 1 c d B .a b 1 d c
C .b a 1 c d D .b a 1 d c
【答案】 D
【详解】 因为当底数大于 1 时,指数函数是定义域上的增函数,
当底数小于 1 时,指数函数是定义域上的减函数,
所以 c ,d 大于 1 ,a ,b 小于 1,
由图知: c1 d1 ,即 c d , b1 a1 ,即 b a ,所以 b a 1 d c ,
12 .(多选) 对函数f(x) 1x2 1 判断正确的是( )
A .增区间 (0, ) B .增区间 ( , 0) C .值域 1 , D.
【答案】 BD
【详解】 根据指数函数性质, f x = 1x 在 , 单调递减,
而 f x x2 1 在 ,0 单调递减,在 0, 单调递增,
故 f(x) 1 x2 1 增区间为 ,0 ; f x x2 1 值域为 1, ,
而 f(x) x2 1 在 , 单调递减,故 f(x) x2 1 值域为 0, .
1
2
13 .(多选) 已知函数f x ,则下面几个结论正确的有( )
A .f x 的图象关于原点对称
C . f x 的值域为 1, 1
B .f x 的图象关于y 轴对称
x1 , x2 R ,且x1 x2 , f x1 f x2
x x
(
2
) (
x
x
) (
1
2
1
2
1
t
) (
3
3
) (
1
2
1
2
1
2
,
) (
1
2
1
2
) (
2
) (
2
x
1
2
·
x
) (
1
2
2
2
1
2
) (
2
x
1
2
)【答案】 AD
【详解】 对于 A , f(x) 则 f(x) f(x)
则f(x) 为奇函数,故图象关于原点对称,故 A 正确.
对于 B ,计算f(1) 1 , f( 1) 1 f(1) ,故f(x) 的图象不关于y 轴对称,故 B 错误.
对于 C , f(x) 1 , 1 2x t, t (1, ) ,
故 y f(x) 1 ,易知: 1 ( 1, 1) ,故 f(x) 的值域为 ( 1, 1) ,故 C 错误.
对 D , f(x) 1 2 x ,因为 y 1 2x 在 R 上为增函数, y 1 2 为 (1, ) 上的减函数,
由复合函数的单调性可得f x 在 R 上单调递减,故x1 , x2 R ,且 x1 x2 , f(x1) f(x2 ) 0 恒成立,故 D 正确.
1 2
二、解答题
14 .已知函数f(x)= 1 1 3.
(1)求f(x)的定义域; (2)判断f(x)的奇偶性; (3)求证: f(x)>0.
【详解】(1)由 2x -1≠0 ,得 x≠0.所以函数的定义域为(-∞ ,0)∪(0 ,+∞).
(2)因为函数f(x)的定义域关于原点对称,
f(-x)= ( 1) (x)3
= ( 1 ) x3 ( 1 ) x3 f (x),
所以f(x)为偶函数.
(3)证明: 当 x>0 时, 1 0 ,x3>0 ,所以f(x)>0. 2x 1
因为f(x)为偶函数,所以当 x<0 时,f(x)>0.
综上所述,对于定义域内的任意 x 都有f(x)>0.
15 .已知函数 f(x) ax 2 (a 0, a 1, x 0) 的图像经过点 (3, 0.5) ,
(1)求 a 值; (2)求函数 f(x) ax 2 (x 0) 的值域;
1
【详解】(1)由题意可得 a3 2 0.5 ,解得 a .
2
(2)由(1)可知 f(x) ( 1)x 2 (x 0) ,
因为 0 1 1 ,所以 f x 在[0, ) 上单调递减,
则 f x 在 x 0 时有最大值,所以 f xmax f(0) ()2 4 ,
因为 f x 0 ,所以函数 f x 的值域为 (0, 4] .
第 12 页 共 13 页
人教 A 版( 2019)高一数学必修第一册
(
a
2
9
a
9,
a
) (
3
2
4
) (
4
) (
3
a
4
) (
2
3
) (
5
) (
4
4
11
) (
3
a
4
) (
2
4
) (
3
) (
5
) (
a
3
a
1,
a
)【提升训练】
16 .设函数 f(x) (a 1)a x b(a 0, a 1) ,则函数 f(x) 的单调性( )
人教 A 版( 2019)高一数学必修第一册
第 13 页 共 13 页
A .与 a 有关,且与 b 有关
C .与 a 有关,且与 b 无关
B .与 a 无关,且与 b 有关
D .与 a 无关,且与 b 无关
【答案】 D
【详解】 当 0 a 1时, f(x) (a 1)a x b 单调递增.
当 a 1时, f(x) (a 1)a x b 单调递增.
则 a 0且 a 1 , b R , f(x) (a 1)a x b 的单调性都为单调递增.
所以函数f(x) (a 1)a x b 的单调性与 a,b 无关.
17 .已知函数f(x )=9x ﹣ a 3x+1+a2(x ∈[0 ,1] ,a ∈R),记f(x )的最大值为 g(a). (Ⅰ)求 g(a )解析式;
(Ⅱ)若对于任意 t∈[ ﹣ 2 ,2] ,任意 a ∈R ,不等式 g(a )≥ ﹣ m2+tm 恒成立,求实数 m 的范围.
【解】(Ⅰ)令 u=3x ∈[1 ,3] ,则f(x )=h(u)=u2 ﹣ 3au+a2.
当 ≤2 ,即 a≤ 时,g(a)=h(u)max =h (3)=a2 ﹣ 9a+9;
2 3
当 2 ,即 a> 时,g(a)=h (u)max=h( 1)=a2 ﹣ 3a+1;
4
故 g(a )= ;
3
(Ⅱ)当 a≤ 时,g(a)=a2 ﹣ 9a+9,g(a )min=g( )= ﹣ ;
3 3 9
当 a 时,g(a)=a2 ﹣ 3a+1 ,g(a)min=g( 3 )= ﹣ 5 ;
3 5
因此 g(a)min=g( )= ﹣ ;
2 4
对于任意任意 a ∈R ,不等式 g(a )≥ ﹣m2+tm 恒成立等价于 ﹣ m2+tm≤ ﹣ .
4
令 h (t)=mt ﹣ m2 ,由于 h (t)是关于 t 的一次函数,
故对于任意 t∈[ ﹣ 2 ,2]都有 h(t)≤ ﹣
4
(
h
(2)
5
4
m
8
m
5
0
2
2
)则 h(2) ,即 4m 8m 5 0 ,解得 m≤ ﹣ 5 或 m≥ 5 .
4
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
