2021-2022学年高一上学期数学人教A版(2019)必修第一册4.5 函数的应用(二) 学案
文档属性
| 名称 | 2021-2022学年高一上学期数学人教A版(2019)必修第一册4.5 函数的应用(二) 学案 |
|
|
| 格式 | docx | ||
| 文件大小 | 502.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-04 00:00:00 | ||
图片预览




文档简介
4.5 函数的应用( 二)
1. 了解函数零点的定义、掌握函数零点的判断方法,了解函数零点与方程根的联系。
2. 能用二分法求方程的近似解。
3. 会用已知函数模型解决实际问题。
人教 A 版( 2019)高一数学必修第一册
第 1 页 共 14 页
人教 A 版( 2019)高一数学必修第一册
一、函数零点的概念
对于函数y=f(x) ,我们把使f(x)=0 的实数 x 叫做函数y=f(x)的零点.函数y=f(x)的零点就是方程f(x) =0 的实数根,也就是函数y=f(x)的图象与 x 轴的交点的横坐标.
比如,由于方程f(x)=lg x=0 的解是 x=1 ,所以函数f(x)=lg x 的零点是 1.
函数的零点不是点
二、基本初等函数的零点
函数 零点(或零点个数)
正比例函数y=kx(k≠0) 一个零点 0
反比例函数y (k≠0) x 无零点
一次函数y=kx+b(k≠0) (
k
)一个零点
二次函数y=ax2+bx+c(a≠0) Δ>0 两个零点-b± 2a Δ
Δ=0 一个零点- b 2a
Δ<0 无零点
指数函数y=ax(a>0 ,且 a≠1) 无零点
对数函数y=logax(a>0 ,且 a≠1) 一个零点 1
幂函数y=xα α>0 一个零点 0
α≤0 无零点
三、函数的零点与对应方程的关系
方程f(x) =0 有实根 函数f(x)的图象与 x 轴有交点 函数f(x)有零点.
四、判断(或求)函数的零点
(1)方程法:根据函数零点的定义可知: 函数f(x)的零点,就是方程f(x)=0 的根,因此,判断一个函数 是否有零点,有几个零点,就是判断方程f(x) =0 是否有实数根,有几个实数根.
(
k
) (
b
)
第 2 页 共 14 页
(
1
2
a
) (
c
) (
1
2
a
) (
c
)(2)图象法: 对于利用方程法很难求解的函数的零点问题,可利用函数的图象求解.我们知道,函数 F(x) =f(x)-g(x)的零点就是方程 F(x)=0 即方程f(x)=g(x)的实数根,也就是函数y=f(x)的图象与y=g(x)的图象 的交点的横坐标.这样,我们就将函数 F(x)的零点问题转化为函数f(x)与 g(x)图象的交点问题,作出两个函 数的图象,就可以判断其零点个数.
五、判断零点所在的区间
零点存在性定理:如果函数y=f(x)在区间[a ,b]上的图象是连续不断的一条曲线,并且有f(a) ·f(b)<0, 那么,函数y=f(x)在区间(a,b)内有零点,即存在 c (a,b),使得f(c)=0,这个 c 也就是方程f(x)=0 的根. 确定函数的零点所在的区间时,通常利用零点存在性定理,转化为判断区间两端点对应的函数值的符号是 否相反.但需注意以下几点:
(1) 当函数y=f(x)同时满足:
①函数的图象在区间[a ,b]上是连续曲线;
②f(a)·f(b)<0 .则可判定函数y=f(x)在区间(a ,b)内至少有一个零点,但是不能明确说明有几个.
(2)当函数y=f(x)的图象在区间[a ,b]上是连续的曲线,但是不满足f(a)·f(b)<0 时,函数y=f(x)在区间(a ,b) 内可能存在零点,也可能不存在零点.
例如函数f(x)=x2 在区间[ -1, 1]上有f( -1)·f(1)>0 ,但是它在区间( -1, 1)上存在零点 0.
(3)函数在区间[a ,b]上的图象是连续曲线,且在区间(a ,b)上单调,若满足f(a)·f(b)<0 ,则函数y=f(x)在区 间(a ,b)上有且只有一个零点.
六、一元二次方程的根的分布
(1)一元二次方程的根的零分布
所谓一元二次方程的根的零分布,是指方程的根相对于零的关系.
设一元二次方程 ax2+bx+c=0(a≠0)的两个实根为 x1 ,x2 且 x1≤x2
人教 A 版( 2019)高一数学必修第一册
第 3 页 共 14 页
b2 4ac 0,
①x1>0,x2>0 x1 x2 b 0, a
x x 0.
③x1<0<x2 c <0. a
b2 4ac 0,
②x1<0 ,x2<0 x1 x2 b 0, a
x x 0.
④x1=0,x2>0 c=0 ,且 b <0;x1<0 ,x2=0 c=0 ,且 b >0.
a a
(2)一元二次方程的根的 k 分布
研究一元二次方程的根的 k 分布,一般情况下要从以下三个方面考虑:
①一元二次方程根的判别式.
②对应二次函数区间端点的函数值的正负.
(
b
)人教 A 版( 2019)高一数学必修第一册
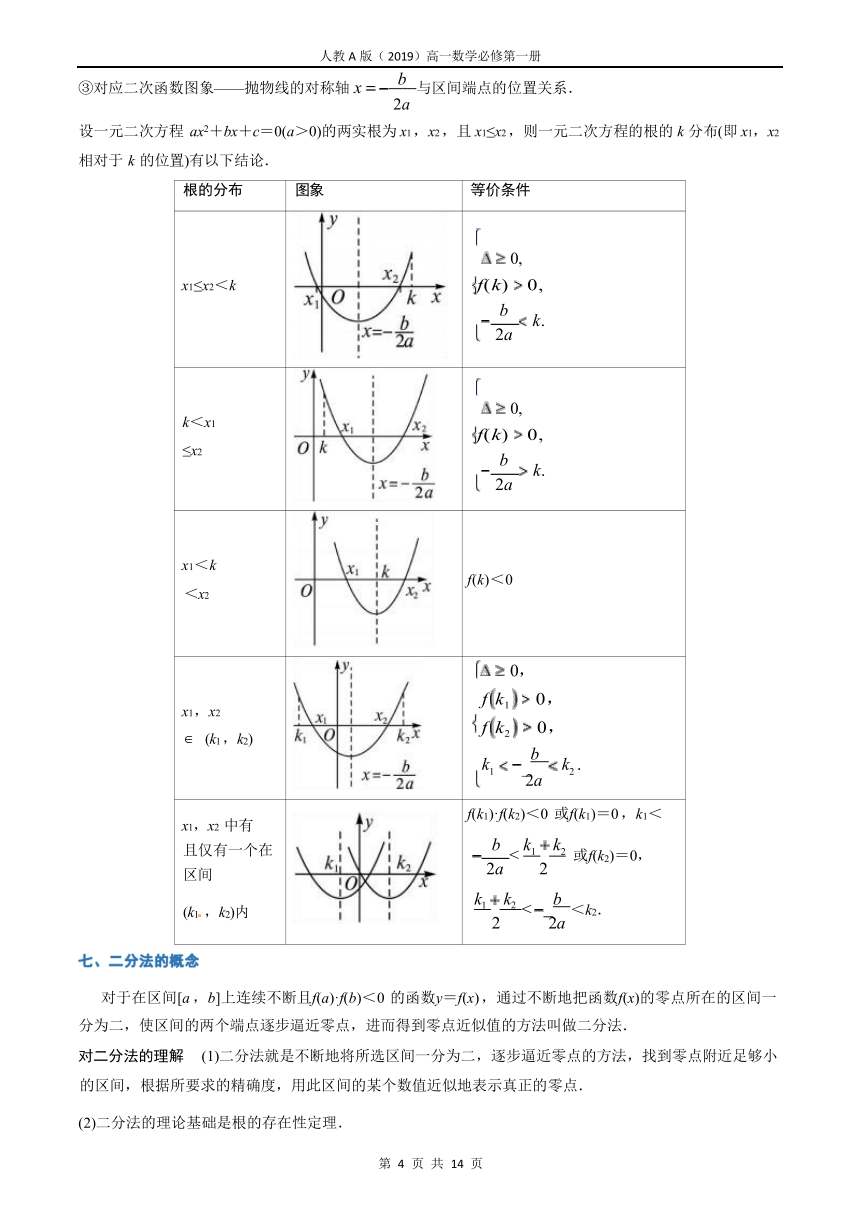
③对应二次函数图象——抛物线的对称轴 x 与区间端点的位置关系.
2a
设一元二次方程 ax2+bx+c=0(a>0)的两实根为 x1 ,x2 ,且 x1≤x2 ,则一元二次方程的根的 k 分布(即 x1,x2 相对于 k 的位置)有以下结论.
根的分布 图象 等价条件
x1≤x2<k (
2
a
) 0, f(k) 0, b k.
k<x1 ≤x2 (
2
a
) 0, f(k) 0, b k.
x1<k <x2 f(k)<0
x1,x2 (k1 ,k2) (
2
a
) 0, f k1 0, f k2 0, k1 b k2 .
x1,x2 中有 且仅有一个在 区间 (k1 ,k2)内 (
2
a
2
) (
2
2
a
)f(k1)·f(k2)<0 或f(k1)=0 ,k1< b < k1 k2 或f(k2)=0, k1 k2 < b <k2.
七、二分法的概念
对于在区间[a ,b]上连续不断且f(a)·f(b)<0 的函数y=f(x) ,通过不断地把函数f(x)的零点所在的区间一
分为二,使区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫做二分法.
对二分法的理解 (1)二分法就是不断地将所选区间一分为二,逐步逼近零点的方法,找到零点附近足够小 的区间,根据所要求的精确度,用此区间的某个数值近似地表示真正的零点.
(2)二分法的理论基础是根的存在性定理.
第 4 页 共 14 页
八、二分法的步骤
(1)使用二分法的前提条件是:
如果函数y=f(x)在选定的区间[a ,b]上的图象是连续不断的一条曲线,并且有f(a)·f(b)<0 ,才能用二分 法去求函数的零点.
(2)给定精确度ε ,用二分法求函数f(x)零点近似值的步骤如下:
①确定区间[a ,b] ,验证f(a)·f(b)<0 ,给定精确度ε;
②求区间(a ,b)的中点 c;
③计算f(c);
a .若f(c)=0 ,则 c 就是函数的零点;
b .若f(a)·f(c)<0 ,则令 b=c(此时零点 x0 (a ,c));
c .若f(c)·f(b)<0 ,则令 a=c(此时零点 x0 (c ,b)).
④判断是否达到精确度ε;即若|a-b|<ε ,则得到零点近似值 a(或 b);否则重复②~④. 用二分法求函数零点近似值的注意点
(1)在第一步中要使:
①区间[a ,b]的长度尽量小;
②f(a),f(b)的值比较容易计算,且f(a) ·f(b)<0.
(2)二分法仅对函数变号零点(即零点两侧某区域内函数值异号)适用.
(3)利用二分法求函数的零点时,要随时进行精确度的判断,以决定是停止计算还是继续计算.
九、利用二分法求方程的近似解
应用二分法求函数零点近似值的方法可以求某些方程的近似解或某些无理数的近似值,其方法是构造函数, 转化为求函数零点近似值的问题.
利用二分法求方程近似解的步骤是: (1)构造函数,利用图象确定方程的根所在的大致区间,通常限制在区 间(n ,n+1) ,nZ;(2)利用二分法求出满足精确度的方程的根所在的区间 M;(3)区间 M 内的任一实数均 是方程的近似解,通常取区间 M 的一个端点.
用二分法求方程的近似解要注意的问题:
(1)要看清题目要求的精确度,它决定着二分法步骤的结束.
(2)初始区间的选定一般在两个整数间,不同的初始区间结果是相同的,但二分的次数却相差较大.
(3)在二分法的第四步,由|a-b|<ε ,便可判断零点近似值为 a 或b ,即只需进行有限次运算即可.
(4)用二分法求出的零点一般是零点的近似值,但并不是所有函数都可以用二分法求零点,必须满足在区间[a, b]上连续不断且f(a) ·f(b)<0 这样条件的函数才能用二分法求得零点的近似值.
十、函数的增长问题
1 、一次函数的增长问题
一次函数y=kx+b(k>0)在区间(0 ,+∞)上是增函数,其增长的速度不变,k 越大,其增长得越快.
人教 A 版( 2019)高一数学必修第一册
第 5 页 共 14 页
人教 A 版( 2019)高一数学必修第一册
第 6 页 共 14 页
2 、对数函数的增长问题
对数函数y=logax(a>1)在区间(0 ,+∞)上是增函数,其增长的速度较慢, 随着 x 的增大,y=logax 的图象类似于与 x 轴“平行”一样,如图所示. 其底数 a 越小,增长的速度越快.
3 、幂函数的增长问题
幂函数y=xn(n>0)在区间(0 ,+∞)上是增函数,其增长速度较快, 其图象如图所示(在第一象限内) ,其指数 n 越大,增长的速度越快.
4 、指数函数的增长问题
指数函数y=ax(a>1)在区间(0 ,+∞)上是增函数,其增长速度最快,
其图象如图所示(在第一象限内).
其底数 a 越大,增长的速度越快.
十一、几类不同增长的函数模型的比较
(1)指数函数、对数函数、幂函数的增长趋势比较
(2) 对数函数y=logax(a>1) ,指数函数y=ax(a>1)与幂函数y=xn(n>0)在区间(0 ,+∞)上都是增函数.
这三类函数的增长是有差异的,我们不妨以函数y=2x,y=x2,y=log2x 为例进行探究.
①在同一坐标系内,作出函数图象,如图 1 .观察归纳结论: y=2x 和y=x2 都比y=log2x 增长得快,
但是y=2x 与y=x2 的增长情况区分度不明显.
②观察y=2x 和y=x2 的增长情况.
在同一坐标系内画出函数y=2x 和y=x2 的图象,如图2. 观察归纳结论: 从图上可观察到y=2x 与y=x2 有两个 交点,有时 2x>x2 ,有时 x2>2x ,但是当自变量越来越 大时,可以看到 2x 的值快速增长,x2 比起 2x 来,几乎 是微不足道的.
一般地,对于指数函数y=ax(a>1)和幂函数y=xn(n>
0) ,通过探索可以发现,在区间(0 ,+∞)上,无论 n 比 a 大多少,尽管在 x 的一定变化范围内,ax 会小于 xn ,但由于 ax 的增长快于 xn 的增长,因此总存在一个 x0, 当 x>x0 时,就会有 ax>xn.
(
1
D.2,
2
) (
5
D.
6
) (
1
C.
6
) (
1
A.
2
)人教 A 版( 2019)高一数学必修第一册
第 7 页 共 14 页
【题型 1 函数的零点】
【例 1】(1)(2021 ·全国) 已知函数
(
1
log
2
x
,
x
1
)f x 2x 1, x 1 ,则函数f(x) 的零点
为( ) A.2 1 C. 2 B. 2 ,0 D.0
(2) 函数f x 4x 2x 2 的零点是( )
(
C
)A. . 1, 0 1 2 B.1 D. 1
(3) 设函数y ax 4 ,(a 0, a 1 ),若其 零点为 2,则 a=__________.
【练习 1-1】 y=2x-1 的图象与x轴的交点坐标及其零点分
别是( )
A.(0, ) , C.(0, ) ,- B.( , 0) , D.( , 0) ,-
【练习 1-2】 若函数y=ax + b(a 0)经过点(2, 0) ,则函数
y = bx2 - ax 的零点是( )
1 1
A.0,2 B.0, C.0, 2 2
【练习 1-3】若x1,x2 是二次函数y x2 5x 6 的两个零点,
(
1
1
)则 的值为( (
)
)
(
1
2
)x x
1
B.
3
【练习 1-4】 若函数 f(x)=ax+1-2a的零点是 1,则 a=___________.
(
3
) (
B.
2,
1
D.
0,
1
) (
B.
1,
2
D.
3,
4
) (
2
) (
B.
(1,
1
)
) (
A.
(1,
2)
) (
B.
4,
1
) (
2
) (
C.
2,
) (
D.
2,
) (
1
)人教 A 版( 2019)高一数学必修第一册
第 8 页 共 14 页
【题型 2 函数的零点区间】
【例 2】(1)(2021 ·贵州省瓮安第二中学)
函数f x 2 x x 2 的零点所在的区间
为( )
A. 3, 2
C. 1, 0
(2) 已知 a是函数h x 2x 8 的零点,则
函数f x ax ln x 5 的零点所在的区间
为( )
A. 0, 1
C. 2, 3
【练习 2-1】 若x0 是函数f x 1x x 的零点,则x0 属于
区间( ).
(
3
2
3
3
2
3
) (
2
1
2
1
1
1
)A. , 1 B. , C. , D. 0,
【练习 2-2】 函数f(x) ln x 2 的零点所在的大致区间是
x
( )
C.(3, 4) D.(2, 3)
e
【练习 2-3】 已知关于x 的方程ax 6 2x 在区间1, 2 内有
解,则实数a 的取值范围是( )
A. 4, 1
1
2
(
B.
1,
0
D.
0,
1
)人教 A 版( 2019)高一数学必修第一册
第 9 页 共 14 页
【题型 3 函数的零点个数】
【例 3】(1) 方程log 1 x x 0根的个数为
2
( )
A.无穷多 B.3 C.1 D.0
(2)(2021 ·全国) 已知函数
(
x
2
x
,
x
0
)f(x) 2 1, x 0 ,若函数
g(x) f (x) m 有 3 个零点,则实数 m的取
值范围( )
A. 1, 0
C.(0,1)
【练习 3-1】 函数f(x) | lg x | 的零点个数为( )
e
A . 0 B . 1 C . 2 D . 3
【练习 3-2】 函数y | x 1| 2x 零点的个数为( )
A . 0 B . 1 C . 2 D . 3
(
【练习
3-3】
ln
x
,
x
0
程
f
x
a
有四个实数根,则实数
a
的取值范围为
(
)
A.
(
,
4)
B.
(0
,
3]
C.
[3,
4)
D.
(0
,
4
)
)已知f(x) x2 2x 3, x 0,若关于 x的方
(
f
(1)
2
f
(1.25)
0.984
f
(1.4375)
0.
162
)人教 A 版( 2019)高一数学必修第一册
第 10 页 共 14 页
【题型 4 指数函数的定点】
【例 4】(2021 ·浙江高一单元测试)根据已给
数据:
x 1.5 3x 的 5.196 近似值 1.53125 5.378 1.5625 5.565 1.625 5.961 1.75 6.839
在精确度为 0.1 的要求下,方程3x x 4 的一
个近似解可以为( )
A. 1 B.1.5 C.1.562 D.1.7
练习 4-1】 若函数f(x) x3 x2 2x 2 的一个零点附近
的函数值如下表:
f (1.5) 0.625
f(1.375) 0.260
f(1.40625) 0.054
则用二分法可求得方程x3 x2 2x 2 0 的一个近似解
(精确度为 0.04) 为( )
A.1.5 B.1.375 C.1.4375 D.1.25
【练习 4-2】 若f x x3 x2 2x 2 的一个正数零点附
近的函数值用二分法逐次计算,数据如下表:
f(1)= -2
f 1.25 0.984
f 1.438 0. 165
f 1.5 0.625
f 1.375 0.260
f 1.4065 0.052
那么方程x3 x2 2x 2 0 的一个近似根(精确到 0.1) 为( )
A.1.2 B.1.3 C.1.4 D.1.5
(
601
x
9000,
x
50
)人教 A 版( 2019)高一数学必修第一册
第 11 页 共 14 页
【题型 5 函数应用模型】
【例 5】 2019 年某开发区一家汽车生产企业
计划引进一批新能源汽车制造设备,通过市
场分析,全年需投入固定成本 3000 万元,
生产x (百辆),需另投入成本C(x) 万元,
10x2 200x, 0 x 50
且C(x) 10000 ,由市
x
场调研知,每辆车售价为 6 万元,且全年内
生产的车辆当年能全部销售完.
(1) 求出 2019 年的利润L(x) (万元) 关于 年产量x (百辆) 的函数关系式;
(2) 2019 年年产量为多少百辆时,企业所 获利润最大? 求出最大利润?
【练习 5-1】 邵东市某宾馆有 50 个房间供游客住宿,当每 个房间的房价为每天 180 元时,房间会全部住满.当每个 房间每天的房价每增加 10 元时,就会有一个房间空闲.宾 馆需对游客居住的每个房间每天支出 20 元的各种费用.根 据规定,每个房间每天的房价不得高于 340 元.设每个房 间的房价每天增加x元(x为 10 的正整数倍).
(1) 设一天订住的房间数为y ,直接写出y 与的函数关系
式及自变量 x的取值范围;
(2) 若一天要保证利润不低于 10800 元,则提高的价格应
该是多少? ;
(3) 在(2) 情况下订住多少个房间时,宾馆的利润最大? 最大利润是多少元?
(
1
x
与
h
x
x
在
0,
上的递减情况说法正确的是(
) (
1
1
1
1
1
1
1
) (
1
1
) (
1
2
)
【基础训练】
1 .若x1,x2 是二次函数y x2 5x 6 的两个零点,则 的值为( )
x x
人教 A 版( 2019)高一数学必修第一册
第 12 页 共 14 页
1
A . 2
1
B . 3
1
C . 6
5
D .
6
2 .函数f x ex1 2 的零点所在的区间是( )
A . 0, 1 B . 1, 2 C . 2, 3 D . 3, 4
3 .函数f x 3x log2 x 的零点所在区间为( )
(
16
8
8
4
4
2
2
)A . , B . , C . , D . , 1
4 .方程log2 x x2 2 的实根个数是( )
A .2 个 B .1 个 C .0 个 D .无穷多个
5 .已知函数f(x) x e x 的部分函数值如下表所示:
x 1 0.5 0.75 0.625 0.5625
f(x) 0.6321 0. 1065 0.2776 0.0897 0.007
那么函数f(x) 的一个零点近似值(精确度为 0. 1)为( )
A .0.45 B .0.57 C .0.78 D .0.89
6 .函数f(x) x lg(x 1) 3零点所在的整区间是( ) A .(0, 1) B .(1, 2) C .(2, 3) D .(3, 4)
7 .若函数f x 2x x 4 的零点所在区间为k, k 1k Z ,则k 的值是( )
A . 1 B . 2 C . 3 D . 4
8 .函数f(x) ln x x2 8的零点所在区间是( )
A .(1, 2) B .(2, 3) C .(3, 4) D .(4, 5)
9.某食品的保鲜时间y(单位: 小时) 与储藏温度 x(单位: C )满足函数关系y eaxb ( e 2.718
为自然对数的底数,a, b 为常数).若该食品在0C 的保鲜时间是 288 小时,在22C 的保鲜时间是 72
小时,则该食品在33C 的保鲜时间是( )
A .24 小时 B .30 小时 C .36 小时 D .48 小时
10.下面对函数f x log x ,g(x) = 2 100 )
(
2
,
2
) (
1
) (
2
) (
)A .f x递减速度越来越慢,gx递减速度越来越快,h x 递减速度比较平稳
B .f x 递减速度越来越快,gx递减速度越来越慢,h x 递减速度越来越快
C .f x 递减速度越来越慢,gx递减速度越来越慢,h x 递减速度比较平稳
D .f x递减速度越来越快,gx递减速度越来越快,h x 递减速度越来越快
11 .若函数y=ax + b(a 0)经过点(2, 0) ,则函数y = bx2 - ax 的零点是( )
人教 A 版( 2019)高一数学必修第一册
第 13 页 共 14 页
A .0 ,2
1
B .0 ,
2
1
C .0 , 2
1
D .2 , 2
12.已知f x 是定义域为R 的奇函数,且在(0, ) 内的零点有 1007 个,则f(x) 的零点的个数为( )
A .1005 B .1006 C .2014 D .2015
13 .方程4x 2x1 4m 0 只有一个实数解,则实数 m 的取值范围是( )
A .{m | m 0} B . m | 0 m C . m | m D .{m | m 0 或m }
14 .已知关于x 的方程ax 6 2x 在区间1, 2 内有解,则实数a 的取值范围是( )
A . 4, 1 B . 4, 1 C . 2, D . 2 1
(
15
.
函数
f
(
x
)
2
x
,
x
0
,
方程
f
(
x
)
c
0
有且只有一个实根,则
c
的取值范围是
(
)
)x2 2x, x 0
A . 1, 0 1, B . 1, 0 1 C . 0, 1 1 D . 1, 1
16.(多选) 下列说法中正确的是( )
A .任取x 0 ,均有3x 2x B .图象经过 2, 的幂函数是偶函数
C .在同一坐标系中,函数y 2x 1与y 2 x 1 的图象关于y 轴对称
D .若方程 l og2x 2 x 的两根分别为 m ,n ,则mn 1
(
17
.某种商品在近
30
天内每件的销售价格
P
(
元
)
和时间
t
(
天
)
的函数关系为:
P
=
t
100,
25
t
30.
) t 20, 0 t 25,
(t∈N*)设该商品的日销售量 Q(件)与时间 t(天)的函数关系为 Q=40 -t(0(
3
) (
A
.
,
6
B
.
,
C
.
,
D
.
,
6
)【提升训练】
(
3
x
4,
x
0
)18 .设函数f(x) x2 6x 6, x 0 ,若互不相等的实数x1 , x2 , x3 满足f x1 f x2 f x3 ,则
x1 x2 x3 的取值范围是( )
11 20 26 20 26 11
3 3 3 3 3 3
(
x
2
x
3,
x
0
,
)19 .已知函数f(x) l (x) , x 0 且关于 x 的函数g(x) f(x) m 有 4 个不同的零点x1 , x2 , x3 , x4 ,
则x1 x2 x3 x4 的取值范围为( )
A .[0, 1) B .[0, 1] C .(0, 1) D .(0, 1]
20 .在数学探究活动中,某兴趣小组合作制作一个工艺品,设计了如图所示的一个窗户,其中矩形 ABCD 的三边AB ,BC ,CD 由长为 8 厘米的材料弯折而成,BC 边的长为2t 厘米(0 t 4 );曲线AOD
2
是一段抛物线,在如图所示的平面直角坐标系中,其解析式为y x ,记窗户
的高(点O 到BC 边的距离)为f t .
(1)求函数f t 的解析式,并求要使得窗户的高最小,BC 边应设计成多少 cm?
人教 A 版( 2019)高一数学必修第一册
(2)要使得窗户的高与BC 长的比值达到最小,BC 边应设计成多少 cm?第 14 页 共 14 页
1. 了解函数零点的定义、掌握函数零点的判断方法,了解函数零点与方程根的联系。
2. 能用二分法求方程的近似解。
3. 会用已知函数模型解决实际问题。
人教 A 版( 2019)高一数学必修第一册
第 1 页 共 14 页
人教 A 版( 2019)高一数学必修第一册
一、函数零点的概念
对于函数y=f(x) ,我们把使f(x)=0 的实数 x 叫做函数y=f(x)的零点.函数y=f(x)的零点就是方程f(x) =0 的实数根,也就是函数y=f(x)的图象与 x 轴的交点的横坐标.
比如,由于方程f(x)=lg x=0 的解是 x=1 ,所以函数f(x)=lg x 的零点是 1.
函数的零点不是点
二、基本初等函数的零点
函数 零点(或零点个数)
正比例函数y=kx(k≠0) 一个零点 0
反比例函数y (k≠0) x 无零点
一次函数y=kx+b(k≠0) (
k
)一个零点
二次函数y=ax2+bx+c(a≠0) Δ>0 两个零点-b± 2a Δ
Δ=0 一个零点- b 2a
Δ<0 无零点
指数函数y=ax(a>0 ,且 a≠1) 无零点
对数函数y=logax(a>0 ,且 a≠1) 一个零点 1
幂函数y=xα α>0 一个零点 0
α≤0 无零点
三、函数的零点与对应方程的关系
方程f(x) =0 有实根 函数f(x)的图象与 x 轴有交点 函数f(x)有零点.
四、判断(或求)函数的零点
(1)方程法:根据函数零点的定义可知: 函数f(x)的零点,就是方程f(x)=0 的根,因此,判断一个函数 是否有零点,有几个零点,就是判断方程f(x) =0 是否有实数根,有几个实数根.
(
k
) (
b
)
第 2 页 共 14 页
(
1
2
a
) (
c
) (
1
2
a
) (
c
)(2)图象法: 对于利用方程法很难求解的函数的零点问题,可利用函数的图象求解.我们知道,函数 F(x) =f(x)-g(x)的零点就是方程 F(x)=0 即方程f(x)=g(x)的实数根,也就是函数y=f(x)的图象与y=g(x)的图象 的交点的横坐标.这样,我们就将函数 F(x)的零点问题转化为函数f(x)与 g(x)图象的交点问题,作出两个函 数的图象,就可以判断其零点个数.
五、判断零点所在的区间
零点存在性定理:如果函数y=f(x)在区间[a ,b]上的图象是连续不断的一条曲线,并且有f(a) ·f(b)<0, 那么,函数y=f(x)在区间(a,b)内有零点,即存在 c (a,b),使得f(c)=0,这个 c 也就是方程f(x)=0 的根. 确定函数的零点所在的区间时,通常利用零点存在性定理,转化为判断区间两端点对应的函数值的符号是 否相反.但需注意以下几点:
(1) 当函数y=f(x)同时满足:
①函数的图象在区间[a ,b]上是连续曲线;
②f(a)·f(b)<0 .则可判定函数y=f(x)在区间(a ,b)内至少有一个零点,但是不能明确说明有几个.
(2)当函数y=f(x)的图象在区间[a ,b]上是连续的曲线,但是不满足f(a)·f(b)<0 时,函数y=f(x)在区间(a ,b) 内可能存在零点,也可能不存在零点.
例如函数f(x)=x2 在区间[ -1, 1]上有f( -1)·f(1)>0 ,但是它在区间( -1, 1)上存在零点 0.
(3)函数在区间[a ,b]上的图象是连续曲线,且在区间(a ,b)上单调,若满足f(a)·f(b)<0 ,则函数y=f(x)在区 间(a ,b)上有且只有一个零点.
六、一元二次方程的根的分布
(1)一元二次方程的根的零分布
所谓一元二次方程的根的零分布,是指方程的根相对于零的关系.
设一元二次方程 ax2+bx+c=0(a≠0)的两个实根为 x1 ,x2 且 x1≤x2
人教 A 版( 2019)高一数学必修第一册
第 3 页 共 14 页
b2 4ac 0,
①x1>0,x2>0 x1 x2 b 0, a
x x 0.
③x1<0<x2 c <0. a
b2 4ac 0,
②x1<0 ,x2<0 x1 x2 b 0, a
x x 0.
④x1=0,x2>0 c=0 ,且 b <0;x1<0 ,x2=0 c=0 ,且 b >0.
a a
(2)一元二次方程的根的 k 分布
研究一元二次方程的根的 k 分布,一般情况下要从以下三个方面考虑:
①一元二次方程根的判别式.
②对应二次函数区间端点的函数值的正负.
(
b
)人教 A 版( 2019)高一数学必修第一册
③对应二次函数图象——抛物线的对称轴 x 与区间端点的位置关系.
2a
设一元二次方程 ax2+bx+c=0(a>0)的两实根为 x1 ,x2 ,且 x1≤x2 ,则一元二次方程的根的 k 分布(即 x1,x2 相对于 k 的位置)有以下结论.
根的分布 图象 等价条件
x1≤x2<k (
2
a
) 0, f(k) 0, b k.
k<x1 ≤x2 (
2
a
) 0, f(k) 0, b k.
x1<k <x2 f(k)<0
x1,x2 (k1 ,k2) (
2
a
) 0, f k1 0, f k2 0, k1 b k2 .
x1,x2 中有 且仅有一个在 区间 (k1 ,k2)内 (
2
a
2
) (
2
2
a
)f(k1)·f(k2)<0 或f(k1)=0 ,k1< b < k1 k2 或f(k2)=0, k1 k2 < b <k2.
七、二分法的概念
对于在区间[a ,b]上连续不断且f(a)·f(b)<0 的函数y=f(x) ,通过不断地把函数f(x)的零点所在的区间一
分为二,使区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫做二分法.
对二分法的理解 (1)二分法就是不断地将所选区间一分为二,逐步逼近零点的方法,找到零点附近足够小 的区间,根据所要求的精确度,用此区间的某个数值近似地表示真正的零点.
(2)二分法的理论基础是根的存在性定理.
第 4 页 共 14 页
八、二分法的步骤
(1)使用二分法的前提条件是:
如果函数y=f(x)在选定的区间[a ,b]上的图象是连续不断的一条曲线,并且有f(a)·f(b)<0 ,才能用二分 法去求函数的零点.
(2)给定精确度ε ,用二分法求函数f(x)零点近似值的步骤如下:
①确定区间[a ,b] ,验证f(a)·f(b)<0 ,给定精确度ε;
②求区间(a ,b)的中点 c;
③计算f(c);
a .若f(c)=0 ,则 c 就是函数的零点;
b .若f(a)·f(c)<0 ,则令 b=c(此时零点 x0 (a ,c));
c .若f(c)·f(b)<0 ,则令 a=c(此时零点 x0 (c ,b)).
④判断是否达到精确度ε;即若|a-b|<ε ,则得到零点近似值 a(或 b);否则重复②~④. 用二分法求函数零点近似值的注意点
(1)在第一步中要使:
①区间[a ,b]的长度尽量小;
②f(a),f(b)的值比较容易计算,且f(a) ·f(b)<0.
(2)二分法仅对函数变号零点(即零点两侧某区域内函数值异号)适用.
(3)利用二分法求函数的零点时,要随时进行精确度的判断,以决定是停止计算还是继续计算.
九、利用二分法求方程的近似解
应用二分法求函数零点近似值的方法可以求某些方程的近似解或某些无理数的近似值,其方法是构造函数, 转化为求函数零点近似值的问题.
利用二分法求方程近似解的步骤是: (1)构造函数,利用图象确定方程的根所在的大致区间,通常限制在区 间(n ,n+1) ,nZ;(2)利用二分法求出满足精确度的方程的根所在的区间 M;(3)区间 M 内的任一实数均 是方程的近似解,通常取区间 M 的一个端点.
用二分法求方程的近似解要注意的问题:
(1)要看清题目要求的精确度,它决定着二分法步骤的结束.
(2)初始区间的选定一般在两个整数间,不同的初始区间结果是相同的,但二分的次数却相差较大.
(3)在二分法的第四步,由|a-b|<ε ,便可判断零点近似值为 a 或b ,即只需进行有限次运算即可.
(4)用二分法求出的零点一般是零点的近似值,但并不是所有函数都可以用二分法求零点,必须满足在区间[a, b]上连续不断且f(a) ·f(b)<0 这样条件的函数才能用二分法求得零点的近似值.
十、函数的增长问题
1 、一次函数的增长问题
一次函数y=kx+b(k>0)在区间(0 ,+∞)上是增函数,其增长的速度不变,k 越大,其增长得越快.
人教 A 版( 2019)高一数学必修第一册
第 5 页 共 14 页
人教 A 版( 2019)高一数学必修第一册
第 6 页 共 14 页
2 、对数函数的增长问题
对数函数y=logax(a>1)在区间(0 ,+∞)上是增函数,其增长的速度较慢, 随着 x 的增大,y=logax 的图象类似于与 x 轴“平行”一样,如图所示. 其底数 a 越小,增长的速度越快.
3 、幂函数的增长问题
幂函数y=xn(n>0)在区间(0 ,+∞)上是增函数,其增长速度较快, 其图象如图所示(在第一象限内) ,其指数 n 越大,增长的速度越快.
4 、指数函数的增长问题
指数函数y=ax(a>1)在区间(0 ,+∞)上是增函数,其增长速度最快,
其图象如图所示(在第一象限内).
其底数 a 越大,增长的速度越快.
十一、几类不同增长的函数模型的比较
(1)指数函数、对数函数、幂函数的增长趋势比较
(2) 对数函数y=logax(a>1) ,指数函数y=ax(a>1)与幂函数y=xn(n>0)在区间(0 ,+∞)上都是增函数.
这三类函数的增长是有差异的,我们不妨以函数y=2x,y=x2,y=log2x 为例进行探究.
①在同一坐标系内,作出函数图象,如图 1 .观察归纳结论: y=2x 和y=x2 都比y=log2x 增长得快,
但是y=2x 与y=x2 的增长情况区分度不明显.
②观察y=2x 和y=x2 的增长情况.
在同一坐标系内画出函数y=2x 和y=x2 的图象,如图2. 观察归纳结论: 从图上可观察到y=2x 与y=x2 有两个 交点,有时 2x>x2 ,有时 x2>2x ,但是当自变量越来越 大时,可以看到 2x 的值快速增长,x2 比起 2x 来,几乎 是微不足道的.
一般地,对于指数函数y=ax(a>1)和幂函数y=xn(n>
0) ,通过探索可以发现,在区间(0 ,+∞)上,无论 n 比 a 大多少,尽管在 x 的一定变化范围内,ax 会小于 xn ,但由于 ax 的增长快于 xn 的增长,因此总存在一个 x0, 当 x>x0 时,就会有 ax>xn.
(
1
D.2,
2
) (
5
D.
6
) (
1
C.
6
) (
1
A.
2
)人教 A 版( 2019)高一数学必修第一册
第 7 页 共 14 页
【题型 1 函数的零点】
【例 1】(1)(2021 ·全国) 已知函数
(
1
log
2
x
,
x
1
)f x 2x 1, x 1 ,则函数f(x) 的零点
为( ) A.2 1 C. 2 B. 2 ,0 D.0
(2) 函数f x 4x 2x 2 的零点是( )
(
C
)A. . 1, 0 1 2 B.1 D. 1
(3) 设函数y ax 4 ,(a 0, a 1 ),若其 零点为 2,则 a=__________.
【练习 1-1】 y=2x-1 的图象与x轴的交点坐标及其零点分
别是( )
A.(0, ) , C.(0, ) ,- B.( , 0) , D.( , 0) ,-
【练习 1-2】 若函数y=ax + b(a 0)经过点(2, 0) ,则函数
y = bx2 - ax 的零点是( )
1 1
A.0,2 B.0, C.0, 2 2
【练习 1-3】若x1,x2 是二次函数y x2 5x 6 的两个零点,
(
1
1
)则 的值为( (
)
)
(
1
2
)x x
1
B.
3
【练习 1-4】 若函数 f(x)=ax+1-2a的零点是 1,则 a=___________.
(
3
) (
B.
2,
1
D.
0,
1
) (
B.
1,
2
D.
3,
4
) (
2
) (
B.
(1,
1
)
) (
A.
(1,
2)
) (
B.
4,
1
) (
2
) (
C.
2,
) (
D.
2,
) (
1
)人教 A 版( 2019)高一数学必修第一册
第 8 页 共 14 页
【题型 2 函数的零点区间】
【例 2】(1)(2021 ·贵州省瓮安第二中学)
函数f x 2 x x 2 的零点所在的区间
为( )
A. 3, 2
C. 1, 0
(2) 已知 a是函数h x 2x 8 的零点,则
函数f x ax ln x 5 的零点所在的区间
为( )
A. 0, 1
C. 2, 3
【练习 2-1】 若x0 是函数f x 1x x 的零点,则x0 属于
区间( ).
(
3
2
3
3
2
3
) (
2
1
2
1
1
1
)A. , 1 B. , C. , D. 0,
【练习 2-2】 函数f(x) ln x 2 的零点所在的大致区间是
x
( )
C.(3, 4) D.(2, 3)
e
【练习 2-3】 已知关于x 的方程ax 6 2x 在区间1, 2 内有
解,则实数a 的取值范围是( )
A. 4, 1
1
2
(
B.
1,
0
D.
0,
1
)人教 A 版( 2019)高一数学必修第一册
第 9 页 共 14 页
【题型 3 函数的零点个数】
【例 3】(1) 方程log 1 x x 0根的个数为
2
( )
A.无穷多 B.3 C.1 D.0
(2)(2021 ·全国) 已知函数
(
x
2
x
,
x
0
)f(x) 2 1, x 0 ,若函数
g(x) f (x) m 有 3 个零点,则实数 m的取
值范围( )
A. 1, 0
C.(0,1)
【练习 3-1】 函数f(x) | lg x | 的零点个数为( )
e
A . 0 B . 1 C . 2 D . 3
【练习 3-2】 函数y | x 1| 2x 零点的个数为( )
A . 0 B . 1 C . 2 D . 3
(
【练习
3-3】
ln
x
,
x
0
程
f
x
a
有四个实数根,则实数
a
的取值范围为
(
)
A.
(
,
4)
B.
(0
,
3]
C.
[3,
4)
D.
(0
,
4
)
)已知f(x) x2 2x 3, x 0,若关于 x的方
(
f
(1)
2
f
(1.25)
0.984
f
(1.4375)
0.
162
)人教 A 版( 2019)高一数学必修第一册
第 10 页 共 14 页
【题型 4 指数函数的定点】
【例 4】(2021 ·浙江高一单元测试)根据已给
数据:
x 1.5 3x 的 5.196 近似值 1.53125 5.378 1.5625 5.565 1.625 5.961 1.75 6.839
在精确度为 0.1 的要求下,方程3x x 4 的一
个近似解可以为( )
A. 1 B.1.5 C.1.562 D.1.7
练习 4-1】 若函数f(x) x3 x2 2x 2 的一个零点附近
的函数值如下表:
f (1.5) 0.625
f(1.375) 0.260
f(1.40625) 0.054
则用二分法可求得方程x3 x2 2x 2 0 的一个近似解
(精确度为 0.04) 为( )
A.1.5 B.1.375 C.1.4375 D.1.25
【练习 4-2】 若f x x3 x2 2x 2 的一个正数零点附
近的函数值用二分法逐次计算,数据如下表:
f(1)= -2
f 1.25 0.984
f 1.438 0. 165
f 1.5 0.625
f 1.375 0.260
f 1.4065 0.052
那么方程x3 x2 2x 2 0 的一个近似根(精确到 0.1) 为( )
A.1.2 B.1.3 C.1.4 D.1.5
(
601
x
9000,
x
50
)人教 A 版( 2019)高一数学必修第一册
第 11 页 共 14 页
【题型 5 函数应用模型】
【例 5】 2019 年某开发区一家汽车生产企业
计划引进一批新能源汽车制造设备,通过市
场分析,全年需投入固定成本 3000 万元,
生产x (百辆),需另投入成本C(x) 万元,
10x2 200x, 0 x 50
且C(x) 10000 ,由市
x
场调研知,每辆车售价为 6 万元,且全年内
生产的车辆当年能全部销售完.
(1) 求出 2019 年的利润L(x) (万元) 关于 年产量x (百辆) 的函数关系式;
(2) 2019 年年产量为多少百辆时,企业所 获利润最大? 求出最大利润?
【练习 5-1】 邵东市某宾馆有 50 个房间供游客住宿,当每 个房间的房价为每天 180 元时,房间会全部住满.当每个 房间每天的房价每增加 10 元时,就会有一个房间空闲.宾 馆需对游客居住的每个房间每天支出 20 元的各种费用.根 据规定,每个房间每天的房价不得高于 340 元.设每个房 间的房价每天增加x元(x为 10 的正整数倍).
(1) 设一天订住的房间数为y ,直接写出y 与的函数关系
式及自变量 x的取值范围;
(2) 若一天要保证利润不低于 10800 元,则提高的价格应
该是多少? ;
(3) 在(2) 情况下订住多少个房间时,宾馆的利润最大? 最大利润是多少元?
(
1
x
与
h
x
x
在
0,
上的递减情况说法正确的是(
) (
1
1
1
1
1
1
1
) (
1
1
) (
1
2
)
【基础训练】
1 .若x1,x2 是二次函数y x2 5x 6 的两个零点,则 的值为( )
x x
人教 A 版( 2019)高一数学必修第一册
第 12 页 共 14 页
1
A . 2
1
B . 3
1
C . 6
5
D .
6
2 .函数f x ex1 2 的零点所在的区间是( )
A . 0, 1 B . 1, 2 C . 2, 3 D . 3, 4
3 .函数f x 3x log2 x 的零点所在区间为( )
(
16
8
8
4
4
2
2
)A . , B . , C . , D . , 1
4 .方程log2 x x2 2 的实根个数是( )
A .2 个 B .1 个 C .0 个 D .无穷多个
5 .已知函数f(x) x e x 的部分函数值如下表所示:
x 1 0.5 0.75 0.625 0.5625
f(x) 0.6321 0. 1065 0.2776 0.0897 0.007
那么函数f(x) 的一个零点近似值(精确度为 0. 1)为( )
A .0.45 B .0.57 C .0.78 D .0.89
6 .函数f(x) x lg(x 1) 3零点所在的整区间是( ) A .(0, 1) B .(1, 2) C .(2, 3) D .(3, 4)
7 .若函数f x 2x x 4 的零点所在区间为k, k 1k Z ,则k 的值是( )
A . 1 B . 2 C . 3 D . 4
8 .函数f(x) ln x x2 8的零点所在区间是( )
A .(1, 2) B .(2, 3) C .(3, 4) D .(4, 5)
9.某食品的保鲜时间y(单位: 小时) 与储藏温度 x(单位: C )满足函数关系y eaxb ( e 2.718
为自然对数的底数,a, b 为常数).若该食品在0C 的保鲜时间是 288 小时,在22C 的保鲜时间是 72
小时,则该食品在33C 的保鲜时间是( )
A .24 小时 B .30 小时 C .36 小时 D .48 小时
10.下面对函数f x log x ,g(x) = 2 100 )
(
2
,
2
) (
1
) (
2
) (
)A .f x递减速度越来越慢,gx递减速度越来越快,h x 递减速度比较平稳
B .f x 递减速度越来越快,gx递减速度越来越慢,h x 递减速度越来越快
C .f x 递减速度越来越慢,gx递减速度越来越慢,h x 递减速度比较平稳
D .f x递减速度越来越快,gx递减速度越来越快,h x 递减速度越来越快
11 .若函数y=ax + b(a 0)经过点(2, 0) ,则函数y = bx2 - ax 的零点是( )
人教 A 版( 2019)高一数学必修第一册
第 13 页 共 14 页
A .0 ,2
1
B .0 ,
2
1
C .0 , 2
1
D .2 , 2
12.已知f x 是定义域为R 的奇函数,且在(0, ) 内的零点有 1007 个,则f(x) 的零点的个数为( )
A .1005 B .1006 C .2014 D .2015
13 .方程4x 2x1 4m 0 只有一个实数解,则实数 m 的取值范围是( )
A .{m | m 0} B . m | 0 m C . m | m D .{m | m 0 或m }
14 .已知关于x 的方程ax 6 2x 在区间1, 2 内有解,则实数a 的取值范围是( )
A . 4, 1 B . 4, 1 C . 2, D . 2 1
(
15
.
函数
f
(
x
)
2
x
,
x
0
,
方程
f
(
x
)
c
0
有且只有一个实根,则
c
的取值范围是
(
)
)x2 2x, x 0
A . 1, 0 1, B . 1, 0 1 C . 0, 1 1 D . 1, 1
16.(多选) 下列说法中正确的是( )
A .任取x 0 ,均有3x 2x B .图象经过 2, 的幂函数是偶函数
C .在同一坐标系中,函数y 2x 1与y 2 x 1 的图象关于y 轴对称
D .若方程 l og2x 2 x 的两根分别为 m ,n ,则mn 1
(
17
.某种商品在近
30
天内每件的销售价格
P
(
元
)
和时间
t
(
天
)
的函数关系为:
P
=
t
100,
25
t
30.
) t 20, 0 t 25,
(t∈N*)设该商品的日销售量 Q(件)与时间 t(天)的函数关系为 Q=40 -t(0
3
) (
A
.
,
6
B
.
,
C
.
,
D
.
,
6
)【提升训练】
(
3
x
4,
x
0
)18 .设函数f(x) x2 6x 6, x 0 ,若互不相等的实数x1 , x2 , x3 满足f x1 f x2 f x3 ,则
x1 x2 x3 的取值范围是( )
11 20 26 20 26 11
3 3 3 3 3 3
(
x
2
x
3,
x
0
,
)19 .已知函数f(x) l (x) , x 0 且关于 x 的函数g(x) f(x) m 有 4 个不同的零点x1 , x2 , x3 , x4 ,
则x1 x2 x3 x4 的取值范围为( )
A .[0, 1) B .[0, 1] C .(0, 1) D .(0, 1]
20 .在数学探究活动中,某兴趣小组合作制作一个工艺品,设计了如图所示的一个窗户,其中矩形 ABCD 的三边AB ,BC ,CD 由长为 8 厘米的材料弯折而成,BC 边的长为2t 厘米(0 t 4 );曲线AOD
2
是一段抛物线,在如图所示的平面直角坐标系中,其解析式为y x ,记窗户
的高(点O 到BC 边的距离)为f t .
(1)求函数f t 的解析式,并求要使得窗户的高最小,BC 边应设计成多少 cm?
人教 A 版( 2019)高一数学必修第一册
(2)要使得窗户的高与BC 长的比值达到最小,BC 边应设计成多少 cm?第 14 页 共 14 页
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
