24.1.2垂直于弦的直径 课件 人教版初中数学九年级上册(共19张ppt)
文档属性
| 名称 | 24.1.2垂直于弦的直径 课件 人教版初中数学九年级上册(共19张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 352.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-02 21:36:47 | ||
图片预览


文档简介
(共19张PPT)
24.1.2垂直于弦的直径
第二十四章 圆
人教版九年级上册
1.探索并理解圆的对称性和垂径定理及其推论;
2. 会运用垂径定理解决有关弦、弧、弦心距以及半径之间的计算或证明问题;
目
标
学
习
学
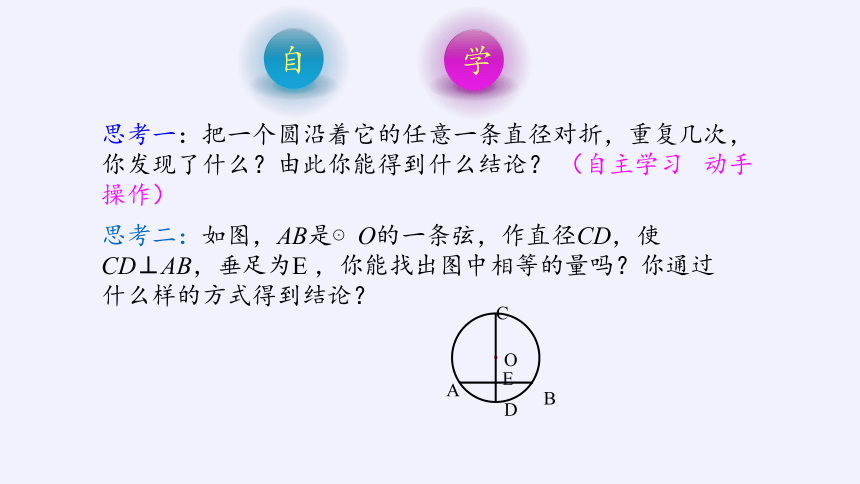
思考一:把一个圆沿着它的任意一条直径对折,重复几次,你发现了什么?由此你能得到什么结论? (自主学习 动手操作)
思考二:如图,AB是⊙O的一条弦,作直径CD,使CD⊥AB,垂足为E ,你能找出图中相等的量吗?你通过什么样的方式得到结论?
·
O
B
A
E
C
D
自
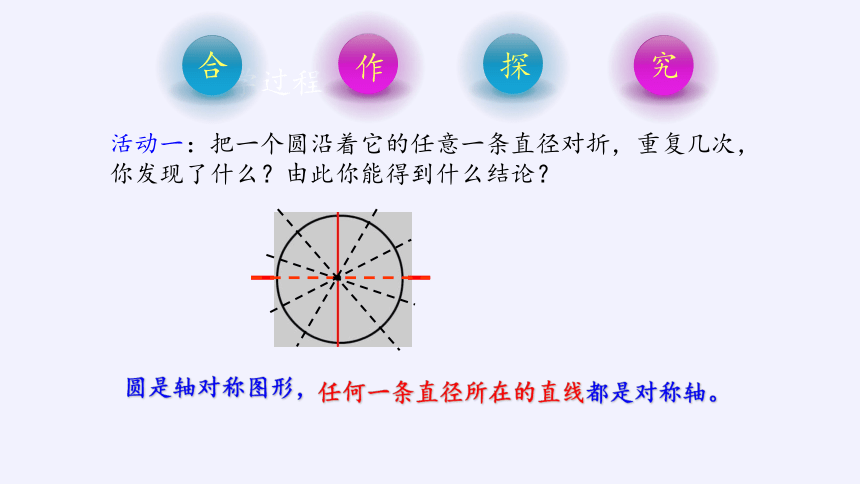
活动一:把一个圆沿着它的任意一条直径对折,重复几次,你发现了什么?由此你能得到什么结论?
圆是轴对称图形,
任何一条直径所在的直线都是对称轴。
教学过程
作
探
合
究
交
流
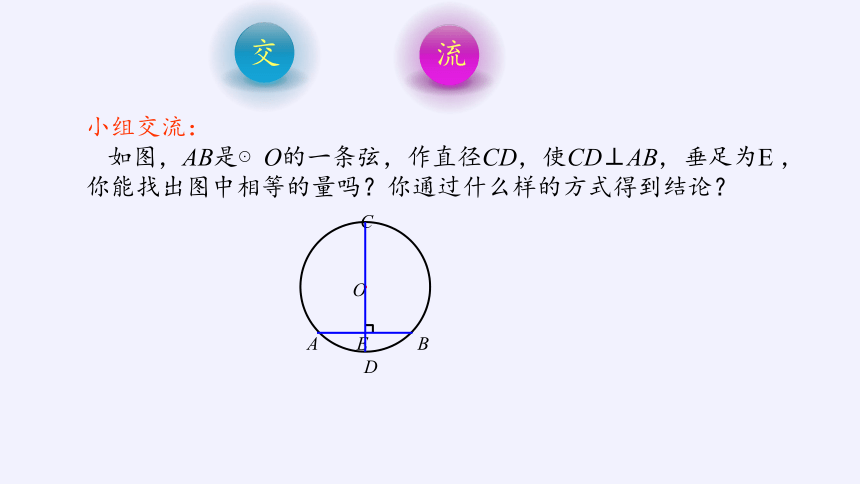
小组交流:
如图,AB是⊙O的一条弦,作直径CD,使CD⊥AB,垂足为E ,你能找出图中相等的量吗?你通过什么样的方式得到结论?
·
O
A
B
C
D
E
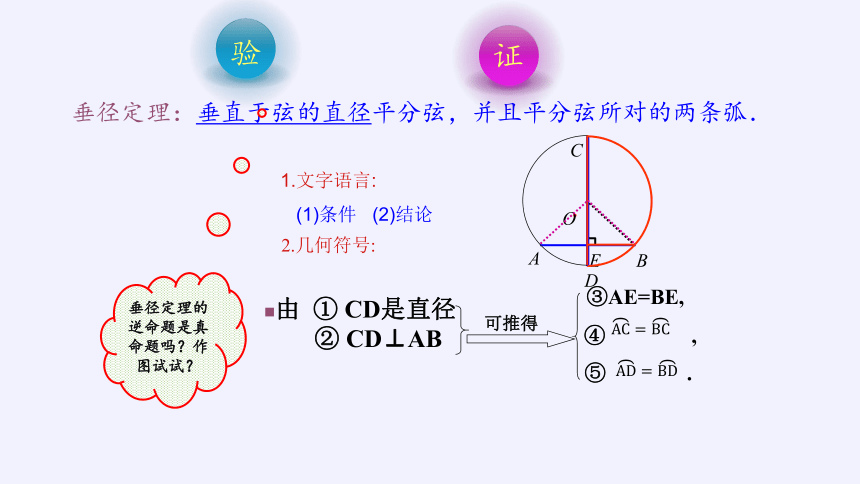
垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧.
·
O
A
B
C
D
E
2.几何符号:
1.文字语言:
(1)条件 (2)结论
垂径定理的逆命题是真命题吗?作图试试?
③AE=BE,
由 ① CD是直径
② CD⊥AB
可推得
⑤ .
④ ,
验
证
验
证
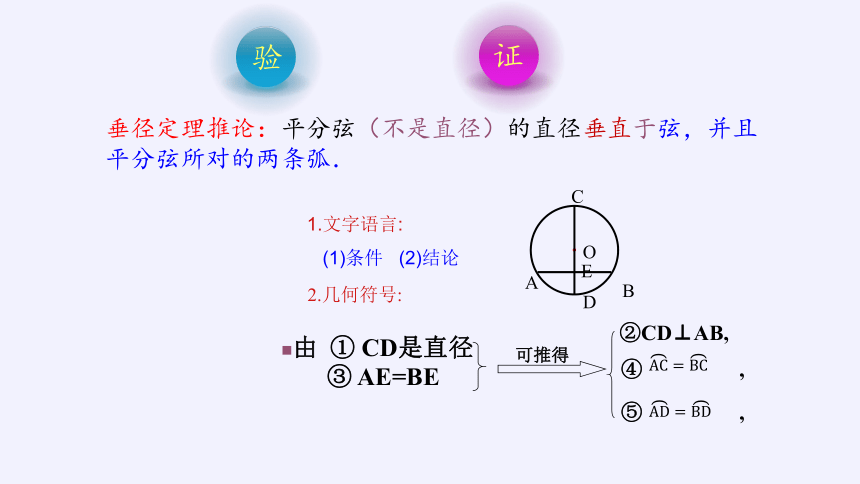
垂径定理推论:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
2.几何符号:
1.文字语言:
(1)条件 (2)结论
·
O
B
A
E
C
D
②CD⊥AB,
由 ① CD是直径
③ AE=BE
④ ,
⑤ ,
可推得
垂径定理
B
A
O
C
D
E
垂直于弦的直径
平分弦,并且平分弦所对的两条弧.
问题:此定理的条件和结论分别是什么?
题设
结论
(2)垂直于弦
}
{
(3)平分弦
(4)平分弦所对的优弧
(5)平分弦所对的劣弧
(1)过圆心
总结归纳
O
讨论
(1)过圆心 (2)垂直于弦
(3)平分弦 (4)平分弦所对优弧 (5)平分弦所对的劣弧
1.若知道“过圆心”和“平分弦”,
你是否能得到另外三个结论?
思考:
2.若知道“垂直于弦”和“平分弦”,
你能得到另外三个结论吗?
O
推论 过圆心平分非直径的弦的直线
垂直于弦,并且平分弦所对的两条弧.
例 : 如图,在⊙O中,弦AB的长为2 cm,圆心O到AB的距离为1cm,求⊙O的半径.
A
B
.
O
E
1
2
在⊙ O中,
若⊙ O的半径、圆心到弦的距离、弦长中,
任意知道两个量,可根据 定理求出第三个量.
勾股
总结:
弦心距2+半弦2=半径2
弦心距
半径
半弦
解
题
例
析
例 : 如图,在⊙O中,弦AB的长为2 cm,圆心O到AB的距离为1cm,求⊙O的半径.
·
O
A
B
E
解:
答:⊙O的半径为2cm.
在Rt△AOE中
判断下列说法的正误
①平分弧的直径必平分弧所对的弦
②平分弦的直线必垂直弦
③垂直于弦的直径平分这条弦
④平分弦的直径垂直于这条弦
⑤弦的垂直平分线是圆的直径
⑥平分弦所对的一条弧的直径必垂直这条弦
⑦在圆中,如果一条直线经过圆心且平分弦,
必平分此弦所对的弧
辨
别
例1:如图所示,在⊙O中,OC⊥AB于C,
OA=2cm,OC=1cm,求弦AB的长。
解题方法总结:
1、见半弦、半径、弦心距三者构造直角三角形来解决;
2、常用辅助线:过圆心作弦的垂线(弦心距)。
练
习
变式练习:
变式 1 在⊙O中,弦AB的长为8,圆心O到AB的距离为3,则⊙O 的半径为
变式2 AB为⊙O的弦,⊙O的半径为5,OC⊥AB于点C,交⊙O于点D,CD=1, 则弦AB的长
变式3 ⊙O的半径为5,弦AB的长为6,则AB的弦心距长为 .
练
习
例2:如图是某风景区的一个圆拱形门,路面AB宽为2米,净高5米,求圆拱形门所在圆的半径是多少米?
练
习
解:连接OA
∵CD⊥AB,且CD过圆心O,
∴AD= AB=1米,∠CDA=90°
在Rt△OAD中,设⊙O的半径为R,则
OA= OC=R,OD=5-R.
由勾股定理,得:OA2=AD2+OD2,即
R2=(5-R)2+12,解得R=2.6.
故圆拱形门所在圆的半径为2.6米.
小
结
说说本节课自己的收获
垂径定理:
垂径定理的推论:
①构造直角三角形,垂径定理和勾股定理有机结合是计算弦长、半径和弦心距等问题的方法.
②技巧:重要辅助线是过圆心作弦的垂线.
重要思路:(由)垂径定理—构造直角三角形—(结合)勾股定理—建立方程.
1.如图,⊙O的直径AB=12,CD是⊙O的弦,CD⊥AB,垂足为P,且BP:AP=1:5,则CD的长为
2.如图,已知⊙O的半径为4,OC垂直弦AB于点C,∠AOB=120°,则弦AB的长为 .
3.如图,在⊙O中,AB、AC是互相垂直的两条弦,OD⊥AB于点D,OE⊥AC于点E,且AB=8cm,AC=6cm,那么⊙O的半径长为
5.如图,⊙O中,直径AB和弦CD相交于点E,AE=2,EB=6,∠DEB=30°,求弦CD长.
.
当
检
4.如图,AB是⊙O的弦,AB长为8,P是⊙O上一个动点(不与A,B重合),过点O作OC⊥AP于点C,OD⊥PB于点D,则CD的长为________.
堂
测
6、如图是一个古代车轮的碎片,小明为求其外圆半径,连结外圆上的两点A、B,并使AB与车轮内圆相切于点D,作CD⊥AB交外圆于点C。测得CD=10cm,AB=60cm,则这个车轮的外圆半径为多少cm?
解:如图,设点O为外圆的圆心,连接OA和OC,
∵CD=10cm,AB=60cm,
∴设半径为r,则OD=r-10,
根据题意得:
解得:r=50。
r2=(r-10)2+302
谢 谢
24.1.2垂直于弦的直径
第二十四章 圆
人教版九年级上册
1.探索并理解圆的对称性和垂径定理及其推论;
2. 会运用垂径定理解决有关弦、弧、弦心距以及半径之间的计算或证明问题;
目
标
学
习
学
思考一:把一个圆沿着它的任意一条直径对折,重复几次,你发现了什么?由此你能得到什么结论? (自主学习 动手操作)
思考二:如图,AB是⊙O的一条弦,作直径CD,使CD⊥AB,垂足为E ,你能找出图中相等的量吗?你通过什么样的方式得到结论?
·
O
B
A
E
C
D
自
活动一:把一个圆沿着它的任意一条直径对折,重复几次,你发现了什么?由此你能得到什么结论?
圆是轴对称图形,
任何一条直径所在的直线都是对称轴。
教学过程
作
探
合
究
交
流
小组交流:
如图,AB是⊙O的一条弦,作直径CD,使CD⊥AB,垂足为E ,你能找出图中相等的量吗?你通过什么样的方式得到结论?
·
O
A
B
C
D
E
垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧.
·
O
A
B
C
D
E
2.几何符号:
1.文字语言:
(1)条件 (2)结论
垂径定理的逆命题是真命题吗?作图试试?
③AE=BE,
由 ① CD是直径
② CD⊥AB
可推得
⑤ .
④ ,
验
证
验
证
垂径定理推论:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
2.几何符号:
1.文字语言:
(1)条件 (2)结论
·
O
B
A
E
C
D
②CD⊥AB,
由 ① CD是直径
③ AE=BE
④ ,
⑤ ,
可推得
垂径定理
B
A
O
C
D
E
垂直于弦的直径
平分弦,并且平分弦所对的两条弧.
问题:此定理的条件和结论分别是什么?
题设
结论
(2)垂直于弦
}
{
(3)平分弦
(4)平分弦所对的优弧
(5)平分弦所对的劣弧
(1)过圆心
总结归纳
O
讨论
(1)过圆心 (2)垂直于弦
(3)平分弦 (4)平分弦所对优弧 (5)平分弦所对的劣弧
1.若知道“过圆心”和“平分弦”,
你是否能得到另外三个结论?
思考:
2.若知道“垂直于弦”和“平分弦”,
你能得到另外三个结论吗?
O
推论 过圆心平分非直径的弦的直线
垂直于弦,并且平分弦所对的两条弧.
例 : 如图,在⊙O中,弦AB的长为2 cm,圆心O到AB的距离为1cm,求⊙O的半径.
A
B
.
O
E
1
2
在⊙ O中,
若⊙ O的半径、圆心到弦的距离、弦长中,
任意知道两个量,可根据 定理求出第三个量.
勾股
总结:
弦心距2+半弦2=半径2
弦心距
半径
半弦
解
题
例
析
例 : 如图,在⊙O中,弦AB的长为2 cm,圆心O到AB的距离为1cm,求⊙O的半径.
·
O
A
B
E
解:
答:⊙O的半径为2cm.
在Rt△AOE中
判断下列说法的正误
①平分弧的直径必平分弧所对的弦
②平分弦的直线必垂直弦
③垂直于弦的直径平分这条弦
④平分弦的直径垂直于这条弦
⑤弦的垂直平分线是圆的直径
⑥平分弦所对的一条弧的直径必垂直这条弦
⑦在圆中,如果一条直线经过圆心且平分弦,
必平分此弦所对的弧
辨
别
例1:如图所示,在⊙O中,OC⊥AB于C,
OA=2cm,OC=1cm,求弦AB的长。
解题方法总结:
1、见半弦、半径、弦心距三者构造直角三角形来解决;
2、常用辅助线:过圆心作弦的垂线(弦心距)。
练
习
变式练习:
变式 1 在⊙O中,弦AB的长为8,圆心O到AB的距离为3,则⊙O 的半径为
变式2 AB为⊙O的弦,⊙O的半径为5,OC⊥AB于点C,交⊙O于点D,CD=1, 则弦AB的长
变式3 ⊙O的半径为5,弦AB的长为6,则AB的弦心距长为 .
练
习
例2:如图是某风景区的一个圆拱形门,路面AB宽为2米,净高5米,求圆拱形门所在圆的半径是多少米?
练
习
解:连接OA
∵CD⊥AB,且CD过圆心O,
∴AD= AB=1米,∠CDA=90°
在Rt△OAD中,设⊙O的半径为R,则
OA= OC=R,OD=5-R.
由勾股定理,得:OA2=AD2+OD2,即
R2=(5-R)2+12,解得R=2.6.
故圆拱形门所在圆的半径为2.6米.
小
结
说说本节课自己的收获
垂径定理:
垂径定理的推论:
①构造直角三角形,垂径定理和勾股定理有机结合是计算弦长、半径和弦心距等问题的方法.
②技巧:重要辅助线是过圆心作弦的垂线.
重要思路:(由)垂径定理—构造直角三角形—(结合)勾股定理—建立方程.
1.如图,⊙O的直径AB=12,CD是⊙O的弦,CD⊥AB,垂足为P,且BP:AP=1:5,则CD的长为
2.如图,已知⊙O的半径为4,OC垂直弦AB于点C,∠AOB=120°,则弦AB的长为 .
3.如图,在⊙O中,AB、AC是互相垂直的两条弦,OD⊥AB于点D,OE⊥AC于点E,且AB=8cm,AC=6cm,那么⊙O的半径长为
5.如图,⊙O中,直径AB和弦CD相交于点E,AE=2,EB=6,∠DEB=30°,求弦CD长.
.
当
检
4.如图,AB是⊙O的弦,AB长为8,P是⊙O上一个动点(不与A,B重合),过点O作OC⊥AP于点C,OD⊥PB于点D,则CD的长为________.
堂
测
6、如图是一个古代车轮的碎片,小明为求其外圆半径,连结外圆上的两点A、B,并使AB与车轮内圆相切于点D,作CD⊥AB交外圆于点C。测得CD=10cm,AB=60cm,则这个车轮的外圆半径为多少cm?
解:如图,设点O为外圆的圆心,连接OA和OC,
∵CD=10cm,AB=60cm,
∴设半径为r,则OD=r-10,
根据题意得:
解得:r=50。
r2=(r-10)2+302
谢 谢
同课章节目录
