人教版数学六年级下册《鸽巢问题》课件(共25张PPT)
文档属性
| 名称 | 人教版数学六年级下册《鸽巢问题》课件(共25张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-01 00:00:00 | ||
图片预览








文档简介
(共25张PPT)
1、把15个球放进4个箱子里,至少有( )个球要放进同一个箱子里。
4
15÷4=3……3
3+1=4(个)
抽屉:4个箱子
物体:15个球
2、47只鸽子飞回8个鸽舍,至少有( )只鸽子要飞进同一个鸽舍。
6
45÷8=5……7
5+1=6(个)
抽屉:8个鸽舍
物体:47只鸽子
3、把红、黄两种颜色的球各6个放到一个袋子里,任意取出5个,至少有( )个同色。
3
5÷2=2……1
2+1=3(个)
抽屉:2种颜色
物体:5个球
4、把红、黄、白三种颜色的球各5个放到一个袋子里,任意取出8个,至少有( )个同色。
3
8÷3=2……2
2+1=3(个)
抽屉:3种颜色
物体:8个球
“抽屉原理”又称“鸽巢原理”,
最先是由19世纪的德国数学家
狄利克雷提出来的,所以又称
“狄利克雷原理”。抽屉原理的应用是千变万化的,用它可以解决许多有趣的问题,并且常常能得到一些令人惊异的结果。
狄利克雷
(1805~1859)
鸽巢问题
——摸球游戏
1、学会利用“抽屉原理”解决简单的实际问题。
2、通过具体应用,加深对“抽屉原理”的理解。
例3:盒子里有同样大小的红球和蓝球各4个。要想摸出的球一定有2个同色的,最少要摸出几个球?
先猜一猜会有什么情况?
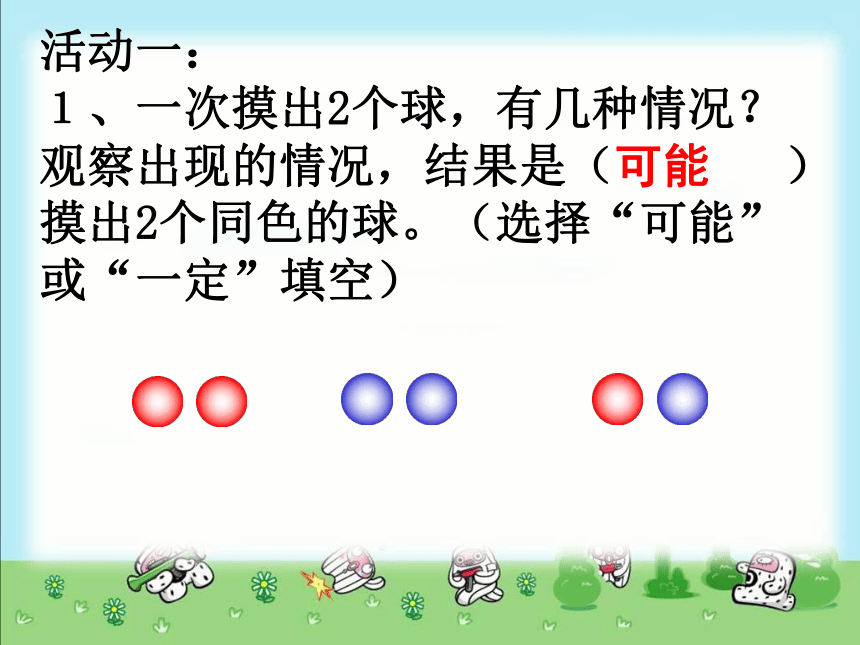
活动一:
1、一次摸出2个球,有几种情况?观察出现的情况,结果是( )摸出2个同色的球。(选择“可能”或“一定”填空)
可能
活动二:
2、一次摸出3个球,有几种情况?观察出现的情况,结果是( )摸出2个同色的球。(选择“可能”或“一定”填空)
一定
请观察,摸出球的个数与颜色种数有什么关系?
摸出球的个数比颜色种数多1。
这种方法在数学上被称之为用“极端思想”:
因为有两种颜色,就先摸两个球,最不利的情况两个是不同颜色的球,这时再摸一个球,无论摸到的是什么颜色的球,都能保证一定有两个球是同色的。 (2+1=3)
小组讨论:
1、在这道题中,什么是“物体”?什么是“抽屉”?什么是“至少数 ”?
2、从题目可知,问题相当于求抽屉原理中的( )?怎样求?
例3:盒子里有同样大小的红球和蓝球各4个。要想摸出的球一定有2个同色的,最少要摸出几个球?
物体数
例3:盒子里有同样大小的红球和蓝球各4个。要想摸出的球一定有 2 个同色的,最少要摸出几个球?
(2-1)×2+1=3(个)
想( )÷2=1……1
2-1=1
抽屉:2种颜色
物体:?个球
至少数:2
把红、黄、蓝、三种颜色的球各10个放到一个袋子里。最少取多少个球,可以保证取到两个颜色相同的球?
(2-1)×3+1=4(个)
抽屉:3种颜色
物体:?个球
至少数:2
物体数=(至少数-1) ×抽屉数+1
知道抽屉数和至少数求物体数时
把红、黄、蓝三种颜色的球各10个放到一个袋子里。最少取多少个球,可以保证取到4个颜色相同的球?
(4-1)×3+1=10(个)
抽屉:3种颜色
物体:?个球
至少数:4
例3:盒子里有同样大小的红球和蓝球各4个。要想摸出的球一定有
个同色的,最少要摸出几个球?
(3-1)×2+1=5(个)
想( )÷2=2……1
3-1=2
抽屉:2种颜色
物体:?个球
至少数:3
2
3
通过这节课的学习,你有什么收获?和大家分享一下吧。
智慧城堡
加油啊!
把红、蓝、黄三种颜色的小棒各10根混在一起。如果让你闭上眼睛,每次最少拿出几根才能保证一定有2根同色的小棒?
把红、蓝、黄三种颜色的小棒各10根混在一起。如果让你闭上眼睛,每次最少拿出几根才能保证一定有3根同色的小棒?
我们学校共有420名同学,至少有( )人的生日是同一天,我们班有36名同学,至少有( )人是同一个月出生的。
箱子里有5种不同品牌的果冻各20粒,要想保证摸到同品牌的果冻4粒,最少要摸出多少粒果冻?
1、把15个球放进4个箱子里,至少有( )个球要放进同一个箱子里。
4
15÷4=3……3
3+1=4(个)
抽屉:4个箱子
物体:15个球
2、47只鸽子飞回8个鸽舍,至少有( )只鸽子要飞进同一个鸽舍。
6
45÷8=5……7
5+1=6(个)
抽屉:8个鸽舍
物体:47只鸽子
3、把红、黄两种颜色的球各6个放到一个袋子里,任意取出5个,至少有( )个同色。
3
5÷2=2……1
2+1=3(个)
抽屉:2种颜色
物体:5个球
4、把红、黄、白三种颜色的球各5个放到一个袋子里,任意取出8个,至少有( )个同色。
3
8÷3=2……2
2+1=3(个)
抽屉:3种颜色
物体:8个球
“抽屉原理”又称“鸽巢原理”,
最先是由19世纪的德国数学家
狄利克雷提出来的,所以又称
“狄利克雷原理”。抽屉原理的应用是千变万化的,用它可以解决许多有趣的问题,并且常常能得到一些令人惊异的结果。
狄利克雷
(1805~1859)
鸽巢问题
——摸球游戏
1、学会利用“抽屉原理”解决简单的实际问题。
2、通过具体应用,加深对“抽屉原理”的理解。
例3:盒子里有同样大小的红球和蓝球各4个。要想摸出的球一定有2个同色的,最少要摸出几个球?
先猜一猜会有什么情况?
活动一:
1、一次摸出2个球,有几种情况?观察出现的情况,结果是( )摸出2个同色的球。(选择“可能”或“一定”填空)
可能
活动二:
2、一次摸出3个球,有几种情况?观察出现的情况,结果是( )摸出2个同色的球。(选择“可能”或“一定”填空)
一定
请观察,摸出球的个数与颜色种数有什么关系?
摸出球的个数比颜色种数多1。
这种方法在数学上被称之为用“极端思想”:
因为有两种颜色,就先摸两个球,最不利的情况两个是不同颜色的球,这时再摸一个球,无论摸到的是什么颜色的球,都能保证一定有两个球是同色的。 (2+1=3)
小组讨论:
1、在这道题中,什么是“物体”?什么是“抽屉”?什么是“至少数 ”?
2、从题目可知,问题相当于求抽屉原理中的( )?怎样求?
例3:盒子里有同样大小的红球和蓝球各4个。要想摸出的球一定有2个同色的,最少要摸出几个球?
物体数
例3:盒子里有同样大小的红球和蓝球各4个。要想摸出的球一定有 2 个同色的,最少要摸出几个球?
(2-1)×2+1=3(个)
想( )÷2=1……1
2-1=1
抽屉:2种颜色
物体:?个球
至少数:2
把红、黄、蓝、三种颜色的球各10个放到一个袋子里。最少取多少个球,可以保证取到两个颜色相同的球?
(2-1)×3+1=4(个)
抽屉:3种颜色
物体:?个球
至少数:2
物体数=(至少数-1) ×抽屉数+1
知道抽屉数和至少数求物体数时
把红、黄、蓝三种颜色的球各10个放到一个袋子里。最少取多少个球,可以保证取到4个颜色相同的球?
(4-1)×3+1=10(个)
抽屉:3种颜色
物体:?个球
至少数:4
例3:盒子里有同样大小的红球和蓝球各4个。要想摸出的球一定有
个同色的,最少要摸出几个球?
(3-1)×2+1=5(个)
想( )÷2=2……1
3-1=2
抽屉:2种颜色
物体:?个球
至少数:3
2
3
通过这节课的学习,你有什么收获?和大家分享一下吧。
智慧城堡
加油啊!
把红、蓝、黄三种颜色的小棒各10根混在一起。如果让你闭上眼睛,每次最少拿出几根才能保证一定有2根同色的小棒?
把红、蓝、黄三种颜色的小棒各10根混在一起。如果让你闭上眼睛,每次最少拿出几根才能保证一定有3根同色的小棒?
我们学校共有420名同学,至少有( )人的生日是同一天,我们班有36名同学,至少有( )人是同一个月出生的。
箱子里有5种不同品牌的果冻各20粒,要想保证摸到同品牌的果冻4粒,最少要摸出多少粒果冻?
