2021-2022学年度华师大版九年级数学下册课件 27.1 圆的认识(第2课时)(共23张ppt)
文档属性
| 名称 | 2021-2022学年度华师大版九年级数学下册课件 27.1 圆的认识(第2课时)(共23张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 807.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-01 00:00:00 | ||
图片预览



文档简介
(共23张PPT)
27.1 圆的认识
(第2课时)
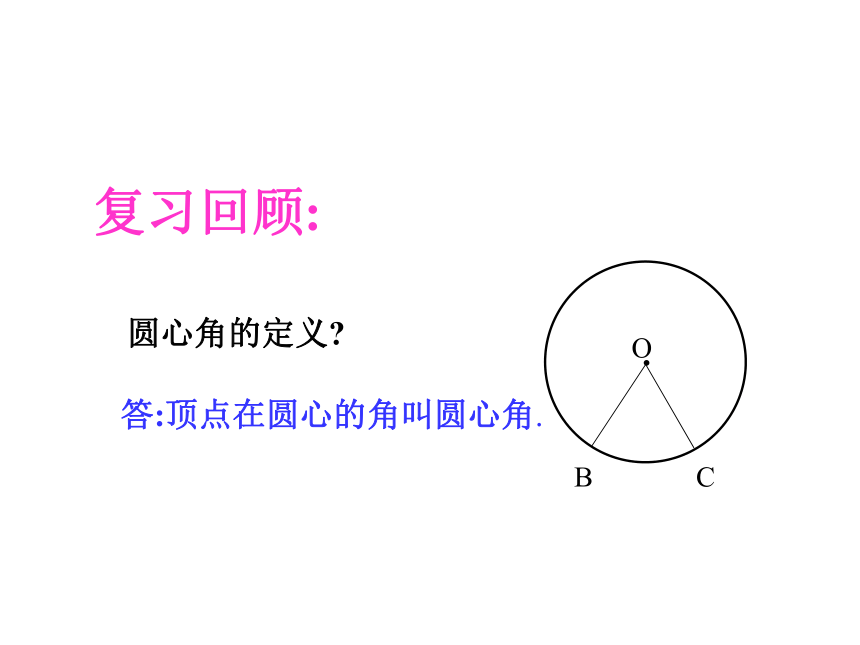
复习回顾:
圆心角的定义
.
O
B
C
答:顶点在圆心的角叫圆心角.
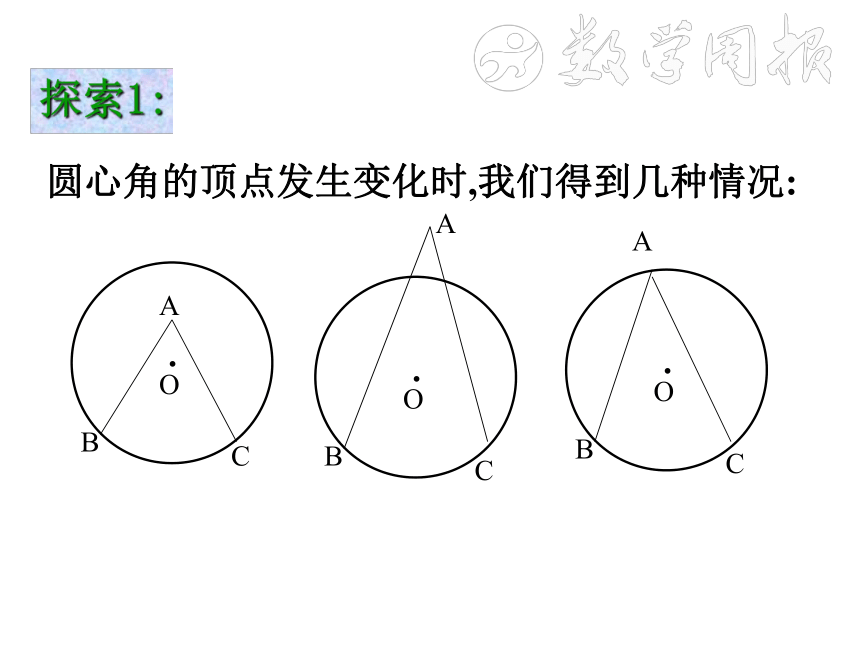
圆心角的顶点发生变化时,我们得到几种情况:
A
.
O
B
C
.
O
B
C
A
.
O
B
C
A
探索1:
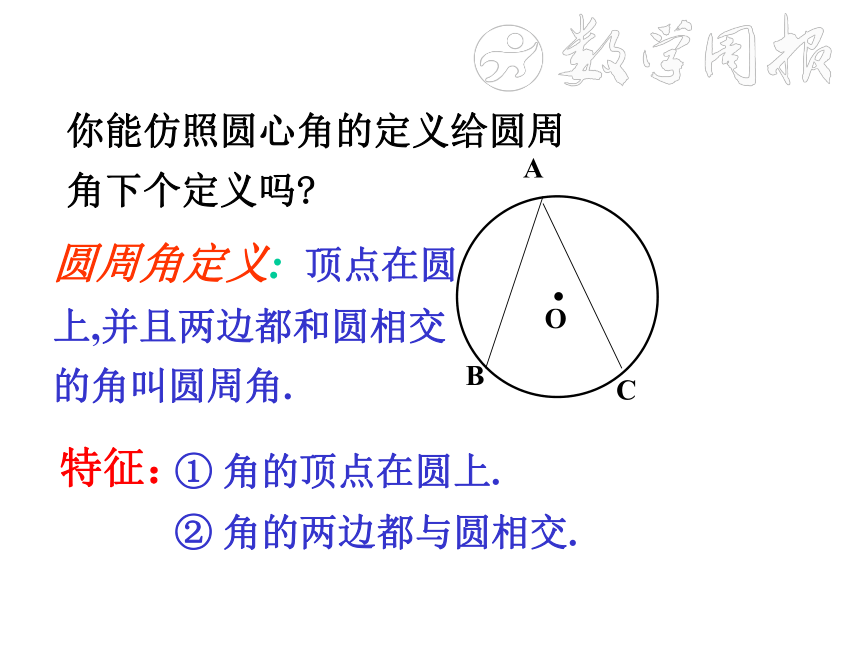
你能仿照圆心角的定义给圆周角下个定义吗
圆周角定义: 顶点在圆上,并且两边都和圆相交的角叫圆周角.
特征:
① 角的顶点在圆上.
② 角的两边都与圆相交.
.
O
B
C
A
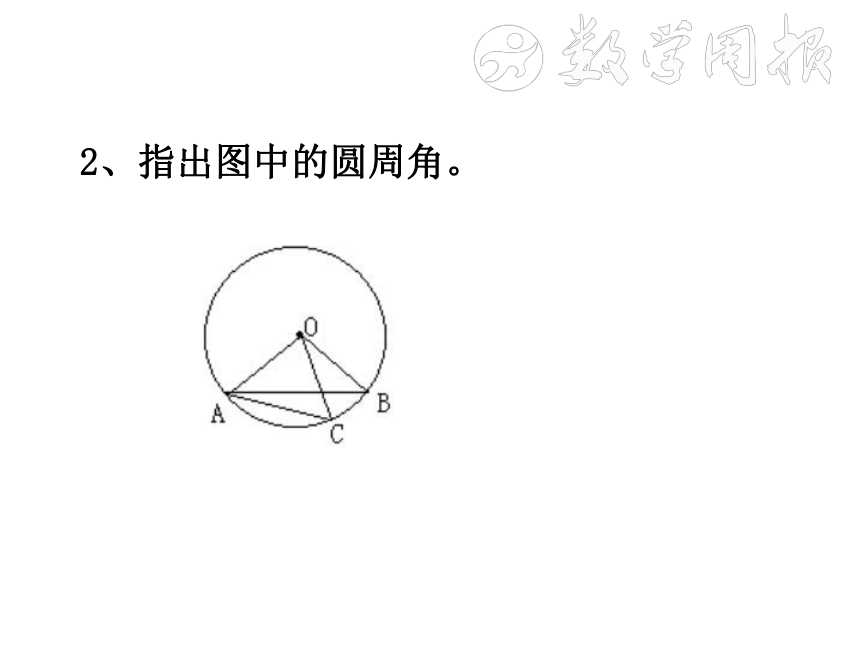
2、指出图中的圆周角。
√
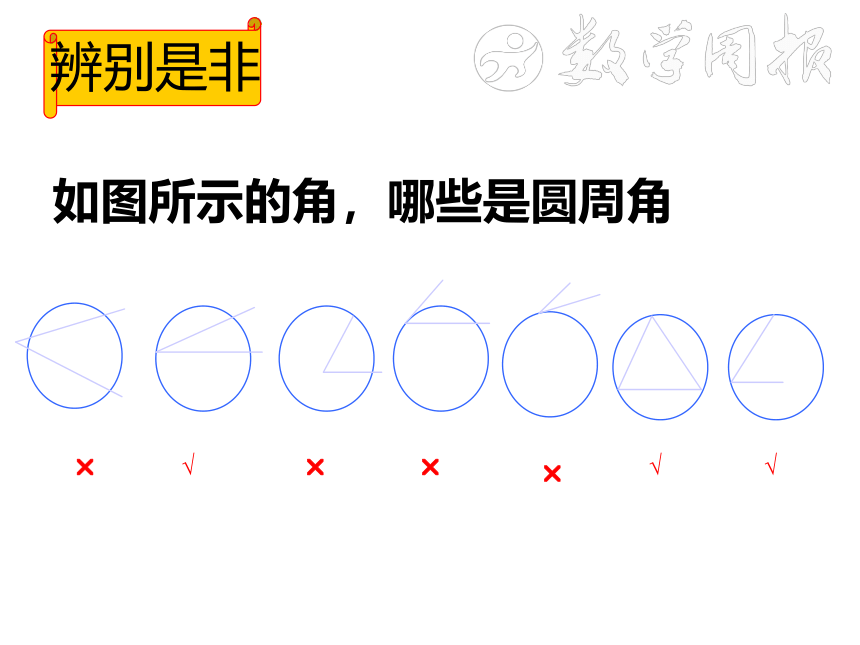
辨别是非
如图所示的角,哪些是圆周角
√
√
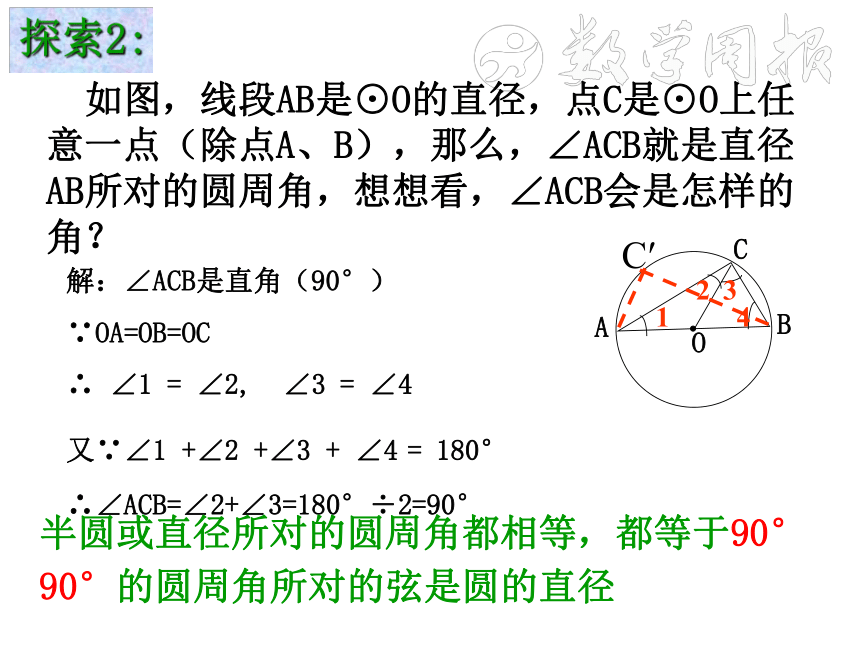
探索2:
如图,线段AB是⊙O的直径,点C是⊙O上任意一点(除点A、B),那么,∠ACB就是直径AB所对的圆周角,想想看,∠ACB会是怎样的角?
O
C
B
A
解:∠ACB是直角(90°)
∵OA=OB=OC
∴ ∠1 = ∠2, ∠3 = ∠4
又∵∠1 +∠2 +∠3 + ∠4 = 180°
∴∠ACB=∠2+∠3=180°÷2=90°
半圆或直径所对的圆周角都相等,都等于90°
90°的圆周角所对的弦是圆的直径
1
2
3
4
C′
O
C
B
A
探索3:
思考:半圆所对的圆周角与它所对的圆心角有关系吗?
讨论:对于一般的弧所对的圆周角,又有怎样规律呢?
画一个圆心角,然后再画同弧所对的圆周角.
1.同一条弧你能画多少个圆周角 多少个圆
心角 用量角器量一量这些
圆周角你有何发现?
2.再用量角器量出圆心角的度数,你有何发现 呢
猜想:一条弧所对的圆周角等于它所对的圆心角的一半.
A
B
O
探索4:
猜想:在同圆(或等圆)中,同弧或等弧所
对的圆周角相等
3.虽然一条弧所对的圆周角有无数个,但它们与圆心的位置有几种情况
O
A
B
C
O
A
B
C
O
A
B
C
分三种情况来证明:
(1)圆心在∠BAC的一边上.
A
O
B
C
1
2
证明:∵ OA=OC
∴ ∠C=∠BAC
∵∠BOC=∠BAC+∠C
∴ ∠BAC= ∠BOC
(2)圆心在∠BAC的内部.
O
A
B
C
D
1
2
1
2
证明:作直径AD.
∵∠BAD= ∠BOD
∠DAC= ∠DOC
∵∠BAD+∠DAC= (∠ BOD+∠DOC)
即: ∠BAC= ∠BOC
1
2
1
2
O
A
B
C
(3)圆心在∠BAC的外部.
D
证明:作直径AD.
∵∠DAB= ∠DOB
∠DAC= ∠DOC
∴ ∠DAC-∠DAB= (∠DOC-∠DOB)
即: ∠BAC= ∠BOC
1
2
1
2
1
2
1
2
结论
在同圆(或等圆)中,同弧或等弧所对的圆周角等于该弧所对的圆心角的一半;
A
B
O
C
D
E
结论:在同圆(或等圆)中,同弧或等弧所对的圆周角相等,相等的圆周角所对的弧相等。
∠D= ∠AOB
∠E= ∠AOB
∠C= ∠AOB
∠D =∠E
∠C=
应用举例
解
例2 如图23.1.12,AB是⊙O的直径,∠A=80°.求∠ABC的度数.
∵AB是⊙O的直径
∴ ∠ACB=90°(直径所对的圆周角是直角)
∴ ∠ABC=180°-∠A-∠ACB
=180°-80°-90°
=10°
例3 试分别求出图中∠x的度数。
2.如图,圆心角∠AOB=100°,
则∠ACB=_ __;
O
A
B
C
1.求圆中角X的度数
B
A
O
.
70°
x
A
O
.
X
120°
练习:
130°
4、在⊙O中,一条弧所对的圆心角和圆周角分别为(2x+100)°和(5x-30)°,则x=_ _;
3. 如图,在直径为AB的半圆中,O为圆心,C、D
为半圆上的两点,∠COD=50°,则
∠CAD=______;
20°
25°
5.AB、AC为⊙O的两条弦,延长CA到D,使 AD=AB,如果∠ADB=35° ,
求∠BOC的度数。
∠BOC =140°
⌒
⌒
1.如图,在⊙O中,BC=2DE, ∠BOC=84°,
求∠ A的度数。
∠A=21°
2. 如何找到一个圆形零件的圆心位置?有什么简捷的方法?
思考:
1.圆周角定义:顶点在圆上,并且两边都和圆相交的角叫圆周角.
3.在同圆(或等圆)中,同弧或等弧所对的圆周角相等,都等于该弧所对的圆心角的一半;相等的圆周角所对的弧相等。
2.半圆或直径所对的圆周角都相等,都等于90°
90°的圆周角所对的弦是圆的直径
小结:
再 见 碑
27.1 圆的认识
(第2课时)
复习回顾:
圆心角的定义
.
O
B
C
答:顶点在圆心的角叫圆心角.
圆心角的顶点发生变化时,我们得到几种情况:
A
.
O
B
C
.
O
B
C
A
.
O
B
C
A
探索1:
你能仿照圆心角的定义给圆周角下个定义吗
圆周角定义: 顶点在圆上,并且两边都和圆相交的角叫圆周角.
特征:
① 角的顶点在圆上.
② 角的两边都与圆相交.
.
O
B
C
A
2、指出图中的圆周角。
√
辨别是非
如图所示的角,哪些是圆周角
√
√
探索2:
如图,线段AB是⊙O的直径,点C是⊙O上任意一点(除点A、B),那么,∠ACB就是直径AB所对的圆周角,想想看,∠ACB会是怎样的角?
O
C
B
A
解:∠ACB是直角(90°)
∵OA=OB=OC
∴ ∠1 = ∠2, ∠3 = ∠4
又∵∠1 +∠2 +∠3 + ∠4 = 180°
∴∠ACB=∠2+∠3=180°÷2=90°
半圆或直径所对的圆周角都相等,都等于90°
90°的圆周角所对的弦是圆的直径
1
2
3
4
C′
O
C
B
A
探索3:
思考:半圆所对的圆周角与它所对的圆心角有关系吗?
讨论:对于一般的弧所对的圆周角,又有怎样规律呢?
画一个圆心角,然后再画同弧所对的圆周角.
1.同一条弧你能画多少个圆周角 多少个圆
心角 用量角器量一量这些
圆周角你有何发现?
2.再用量角器量出圆心角的度数,你有何发现 呢
猜想:一条弧所对的圆周角等于它所对的圆心角的一半.
A
B
O
探索4:
猜想:在同圆(或等圆)中,同弧或等弧所
对的圆周角相等
3.虽然一条弧所对的圆周角有无数个,但它们与圆心的位置有几种情况
O
A
B
C
O
A
B
C
O
A
B
C
分三种情况来证明:
(1)圆心在∠BAC的一边上.
A
O
B
C
1
2
证明:∵ OA=OC
∴ ∠C=∠BAC
∵∠BOC=∠BAC+∠C
∴ ∠BAC= ∠BOC
(2)圆心在∠BAC的内部.
O
A
B
C
D
1
2
1
2
证明:作直径AD.
∵∠BAD= ∠BOD
∠DAC= ∠DOC
∵∠BAD+∠DAC= (∠ BOD+∠DOC)
即: ∠BAC= ∠BOC
1
2
1
2
O
A
B
C
(3)圆心在∠BAC的外部.
D
证明:作直径AD.
∵∠DAB= ∠DOB
∠DAC= ∠DOC
∴ ∠DAC-∠DAB= (∠DOC-∠DOB)
即: ∠BAC= ∠BOC
1
2
1
2
1
2
1
2
结论
在同圆(或等圆)中,同弧或等弧所对的圆周角等于该弧所对的圆心角的一半;
A
B
O
C
D
E
结论:在同圆(或等圆)中,同弧或等弧所对的圆周角相等,相等的圆周角所对的弧相等。
∠D= ∠AOB
∠E= ∠AOB
∠C= ∠AOB
∠D =∠E
∠C=
应用举例
解
例2 如图23.1.12,AB是⊙O的直径,∠A=80°.求∠ABC的度数.
∵AB是⊙O的直径
∴ ∠ACB=90°(直径所对的圆周角是直角)
∴ ∠ABC=180°-∠A-∠ACB
=180°-80°-90°
=10°
例3 试分别求出图中∠x的度数。
2.如图,圆心角∠AOB=100°,
则∠ACB=_ __;
O
A
B
C
1.求圆中角X的度数
B
A
O
.
70°
x
A
O
.
X
120°
练习:
130°
4、在⊙O中,一条弧所对的圆心角和圆周角分别为(2x+100)°和(5x-30)°,则x=_ _;
3. 如图,在直径为AB的半圆中,O为圆心,C、D
为半圆上的两点,∠COD=50°,则
∠CAD=______;
20°
25°
5.AB、AC为⊙O的两条弦,延长CA到D,使 AD=AB,如果∠ADB=35° ,
求∠BOC的度数。
∠BOC =140°
⌒
⌒
1.如图,在⊙O中,BC=2DE, ∠BOC=84°,
求∠ A的度数。
∠A=21°
2. 如何找到一个圆形零件的圆心位置?有什么简捷的方法?
思考:
1.圆周角定义:顶点在圆上,并且两边都和圆相交的角叫圆周角.
3.在同圆(或等圆)中,同弧或等弧所对的圆周角相等,都等于该弧所对的圆心角的一半;相等的圆周角所对的弧相等。
2.半圆或直径所对的圆周角都相等,都等于90°
90°的圆周角所对的弦是圆的直径
小结:
再 见 碑
