人教版数学七年级下册第五章 相交线与平行线:5.2.1平行线的性质教案
文档属性
| 名称 | 人教版数学七年级下册第五章 相交线与平行线:5.2.1平行线的性质教案 |  | |
| 格式 | doc | ||
| 文件大小 | 60.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-03 08:29:49 | ||
图片预览


文档简介
5.3.1 平行线的性质
一、学情分析:
本课是在学行线的判定后学习的内容,学生对平行线与角的关系有了一定的认识,因此要在基本图形中去观察出平行线与同位角、内错角、同旁内角的关系,进而猜测出平行线的性质对学生来说难度不大。但是本课的学习,估计学生会产生以下困难:(1)不知道用何种方法来验证自己猜测的正确性。(2)部分学生对平行线性质和判定理解不清,对性质运用所需要的条件掌握不牢,造成性质的滥用。(3)在性质的运用过程中,由于对几何的推理还比较陌生导致书写的格式出现问题。
二、教学目标
(一)、知识与技能:
1.探索并掌握平行线的性质。
2.能用平行线的性质定理进行简单的计算、证明。
3.知道对平行线的性质和判定进行的区别。
(二)、过程与方法:
1.经历探索直线平行的性质的过程,掌握平行线的三条性质,并能用它们进行简单的推理和计算。
2.经历观察、操作、想像、推理、交流等活动,进一步发展空间观念,推理能力和有条理表达能力。
(三)、情感态度价值观:
1.通过对平行线性质的探究,使学生初步认识数学与现实生活的密切联系,体会科学的思想方法,激发学生探索创新精神。
2.通过师生的共同活动,促使学生在学习活动中培养良好的情感、合作交流、主动参与的意识,在独立思考的同时能够认识他人。三、教学重点
掌握平行线的性质,能用平行线的性质定理进行简单的计算、证明。
4、教学难点
区分平行线的性质和判定.
五、教学准备
三角尺,带有平行线的横格纸
六、课时安排
一课时
七、教学过程
(一)、回顾旧知
问题:平行线的判定方法?
判定方法1: 同位角相等,两直线平行.
判定方法2: 内错角相等,两直线平行.
判定方法3: 同旁内角互补,两直线平行.
(二)、探究1
活动:给学生每人发一张带有平行线的横格纸,让学生自己选择一组平行线,然后画这组平行线的截线,找一个同位角并量出同位角的度数。
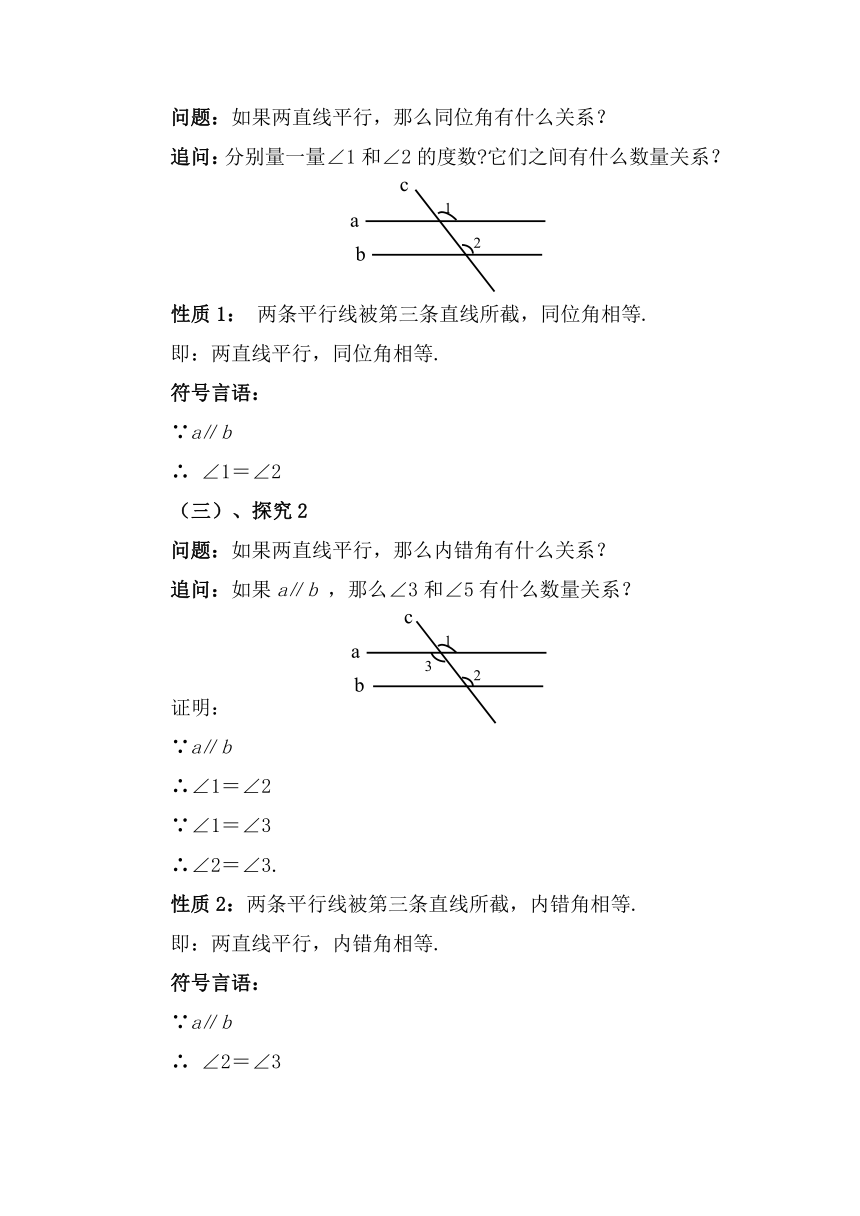
问题:如果两直线平行,那么同位角有什么关系?
追问:分别量一量∠1和∠2的度数 它们之间有什么数量关系?
性质1: 两条平行线被第三条直线所截,同位角相等.
即:两直线平行,同位角相等.
符号言语:
∵a∥b
∴ ∠1=∠2
(三)、探究2
问题:如果两直线平行,那么内错角有什么关系?
追问:如果a∥b ,那么∠3和∠5有什么数量关系?
证明:
∵a∥b
∴∠1=∠2
∵∠1=∠3
∴∠2=∠3.
性质2:两条平行线被第三条直线所截,内错角相等.
即:两直线平行,内错角相等.
符号言语:
∵a∥b
∴ ∠2=∠3
(四)、探究3
问题:如果两直线平行,那么同旁内角有什么关系?
追问:如果a∥b ,那么∠2和∠4有什么数量关系?
证明:
∵a∥b
∴∠1=∠2
∵∠1+∠4=180°
∴∠2+∠4=180°
性质3:两条平行线被第三条直线所截,同旁内角互补.
即:两直线平行,同旁内角互补.
符号言语:
∵a∥b
∴∠2+∠4=180°
练习1:
如图,平行线AB,CD被直线AE所截.(图形PPT展示)
(1)从∠1=110 .可以知道∠3是多少度吗?为什么?
(2)从∠1=110 .可以知道∠2是多少度吗?为什么?
(3)从∠1=110 .可以知道∠4是多少度吗?为什么?
解:(1)∠3=110 .
理由如下:
∵AB∥CD,
∴∠1=∠3(两直线平行,同位角相等)
∵∠1=110 ,
∴∠3=110 .
(2)∠2=110 .
理由如下:
∵AB∥CD,
∴∠1=∠2(两直线平行,内错角相等)
∵ ∠1=110 ,
∴∠2 =110 .
(3)∠4=70 .
理由如下:
∵AB∥CD,
∴ ∠1+∠4=180 (两直线平行,同旁内角互补)
∵∠1=110 ,
∴∠4=70 .
(五)、应用提高
例:如图,是一块梯形铁片的残余部分,量得∠A=100 ,∠B=115 ,梯形的另外两个角分别是多少度?
追问:梯形的上、下两底有什么位置关系?(平行)
解:∵AB∥CD ,
∴∠A+∠D =180 ,∠B+∠C =180 .
(两直线平行,同旁内角互补)
∴∠D =180 -∠A
=180 -100 =80 ,
∠C =180 -∠B
=180 -115 =65 .
∴梯形的另外两个角分别是80 ,65 .
练习2:
1. 已知∠3 =∠4,∠1=47°, 求∠2的度数?
解:∵∠3 =∠4(已知 )
∴a∥b(同位角相等,两直线平行)
∴∠1=∠2(两直线平行,同位角相等)
∵∠1= 47°(已知 )
∴∠2= 47°(等量代换)
练习3:
已知,如图,∠1=∠2,CE∥BF,
求证: AB∥CD.
证明:
∵ CE∥BF ( 已知 )
∴∠1=∠B ( )
∵∠1=∠2 ( 已知 )
∴∠2=∠B.( )
∵∠2和∠B是内错角,
∴ AB∥CD( ).
8、板书设计
平行线的性质
性质1:两直线平行,同位角相等.
性质2:两直线平行,内位角相等.
性质3:两直线平行,同旁内角相等.
九、小结归纳
性质
两直线平行
判定
十、布置作业
教材23页习题5.3第4、6题.
c
a
2
1
b
c
a
3
2
1
b
c
a
4
3
2
1
b
同位角相等
内错角相等
同旁内角互补
一、学情分析:
本课是在学行线的判定后学习的内容,学生对平行线与角的关系有了一定的认识,因此要在基本图形中去观察出平行线与同位角、内错角、同旁内角的关系,进而猜测出平行线的性质对学生来说难度不大。但是本课的学习,估计学生会产生以下困难:(1)不知道用何种方法来验证自己猜测的正确性。(2)部分学生对平行线性质和判定理解不清,对性质运用所需要的条件掌握不牢,造成性质的滥用。(3)在性质的运用过程中,由于对几何的推理还比较陌生导致书写的格式出现问题。
二、教学目标
(一)、知识与技能:
1.探索并掌握平行线的性质。
2.能用平行线的性质定理进行简单的计算、证明。
3.知道对平行线的性质和判定进行的区别。
(二)、过程与方法:
1.经历探索直线平行的性质的过程,掌握平行线的三条性质,并能用它们进行简单的推理和计算。
2.经历观察、操作、想像、推理、交流等活动,进一步发展空间观念,推理能力和有条理表达能力。
(三)、情感态度价值观:
1.通过对平行线性质的探究,使学生初步认识数学与现实生活的密切联系,体会科学的思想方法,激发学生探索创新精神。
2.通过师生的共同活动,促使学生在学习活动中培养良好的情感、合作交流、主动参与的意识,在独立思考的同时能够认识他人。三、教学重点
掌握平行线的性质,能用平行线的性质定理进行简单的计算、证明。
4、教学难点
区分平行线的性质和判定.
五、教学准备
三角尺,带有平行线的横格纸
六、课时安排
一课时
七、教学过程
(一)、回顾旧知
问题:平行线的判定方法?
判定方法1: 同位角相等,两直线平行.
判定方法2: 内错角相等,两直线平行.
判定方法3: 同旁内角互补,两直线平行.
(二)、探究1
活动:给学生每人发一张带有平行线的横格纸,让学生自己选择一组平行线,然后画这组平行线的截线,找一个同位角并量出同位角的度数。
问题:如果两直线平行,那么同位角有什么关系?
追问:分别量一量∠1和∠2的度数 它们之间有什么数量关系?
性质1: 两条平行线被第三条直线所截,同位角相等.
即:两直线平行,同位角相等.
符号言语:
∵a∥b
∴ ∠1=∠2
(三)、探究2
问题:如果两直线平行,那么内错角有什么关系?
追问:如果a∥b ,那么∠3和∠5有什么数量关系?
证明:
∵a∥b
∴∠1=∠2
∵∠1=∠3
∴∠2=∠3.
性质2:两条平行线被第三条直线所截,内错角相等.
即:两直线平行,内错角相等.
符号言语:
∵a∥b
∴ ∠2=∠3
(四)、探究3
问题:如果两直线平行,那么同旁内角有什么关系?
追问:如果a∥b ,那么∠2和∠4有什么数量关系?
证明:
∵a∥b
∴∠1=∠2
∵∠1+∠4=180°
∴∠2+∠4=180°
性质3:两条平行线被第三条直线所截,同旁内角互补.
即:两直线平行,同旁内角互补.
符号言语:
∵a∥b
∴∠2+∠4=180°
练习1:
如图,平行线AB,CD被直线AE所截.(图形PPT展示)
(1)从∠1=110 .可以知道∠3是多少度吗?为什么?
(2)从∠1=110 .可以知道∠2是多少度吗?为什么?
(3)从∠1=110 .可以知道∠4是多少度吗?为什么?
解:(1)∠3=110 .
理由如下:
∵AB∥CD,
∴∠1=∠3(两直线平行,同位角相等)
∵∠1=110 ,
∴∠3=110 .
(2)∠2=110 .
理由如下:
∵AB∥CD,
∴∠1=∠2(两直线平行,内错角相等)
∵ ∠1=110 ,
∴∠2 =110 .
(3)∠4=70 .
理由如下:
∵AB∥CD,
∴ ∠1+∠4=180 (两直线平行,同旁内角互补)
∵∠1=110 ,
∴∠4=70 .
(五)、应用提高
例:如图,是一块梯形铁片的残余部分,量得∠A=100 ,∠B=115 ,梯形的另外两个角分别是多少度?
追问:梯形的上、下两底有什么位置关系?(平行)
解:∵AB∥CD ,
∴∠A+∠D =180 ,∠B+∠C =180 .
(两直线平行,同旁内角互补)
∴∠D =180 -∠A
=180 -100 =80 ,
∠C =180 -∠B
=180 -115 =65 .
∴梯形的另外两个角分别是80 ,65 .
练习2:
1. 已知∠3 =∠4,∠1=47°, 求∠2的度数?
解:∵∠3 =∠4(已知 )
∴a∥b(同位角相等,两直线平行)
∴∠1=∠2(两直线平行,同位角相等)
∵∠1= 47°(已知 )
∴∠2= 47°(等量代换)
练习3:
已知,如图,∠1=∠2,CE∥BF,
求证: AB∥CD.
证明:
∵ CE∥BF ( 已知 )
∴∠1=∠B ( )
∵∠1=∠2 ( 已知 )
∴∠2=∠B.( )
∵∠2和∠B是内错角,
∴ AB∥CD( ).
8、板书设计
平行线的性质
性质1:两直线平行,同位角相等.
性质2:两直线平行,内位角相等.
性质3:两直线平行,同旁内角相等.
九、小结归纳
性质
两直线平行
判定
十、布置作业
教材23页习题5.3第4、6题.
c
a
2
1
b
c
a
3
2
1
b
c
a
4
3
2
1
b
同位角相等
内错角相等
同旁内角互补
