3.2.1双曲线的标准方程(1)课件-2021-2022学年高二数学苏教版(2019)选择性必修第一册(共18张PPT)
文档属性
| 名称 | 3.2.1双曲线的标准方程(1)课件-2021-2022学年高二数学苏教版(2019)选择性必修第一册(共18张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-03 20:08:09 | ||
图片预览




文档简介
(共18张PPT)
3.2 双曲线?
3.2.1双曲线的标准方程(1)?
创设情境
发电厂冷却塔轴截面的外轮廓线的形状是双曲线.用点光源照射一个放在地面上的球,适当调整点光源的位置,球在地面上影子的外轮廓线可以是双曲线的一部分.
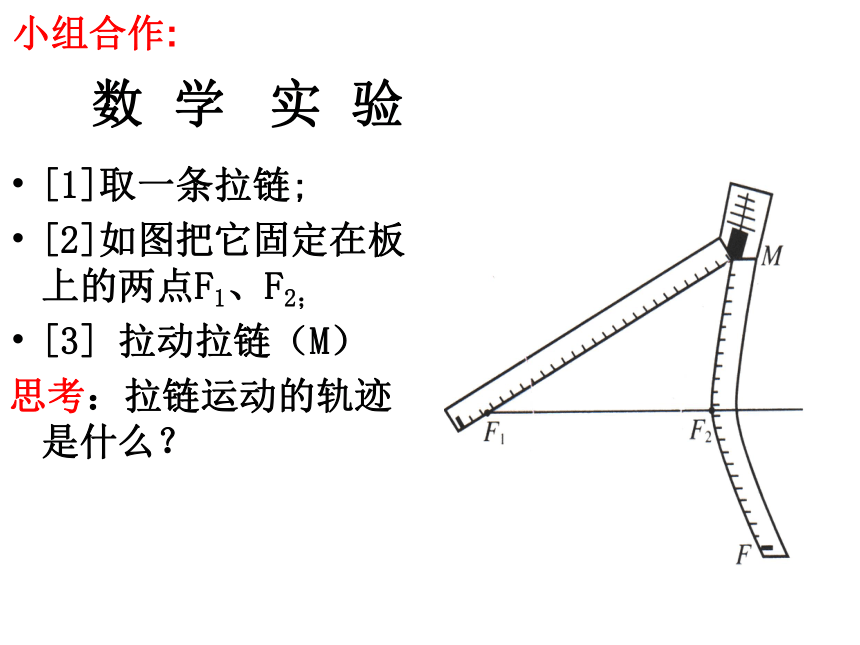
数 学 实 验
[1]取一条拉链;
[2]如图把它固定在板上的两点F1、F2;
[3] 拉动拉链(M)
思考:拉链运动的轨迹是什么?
小组合作:
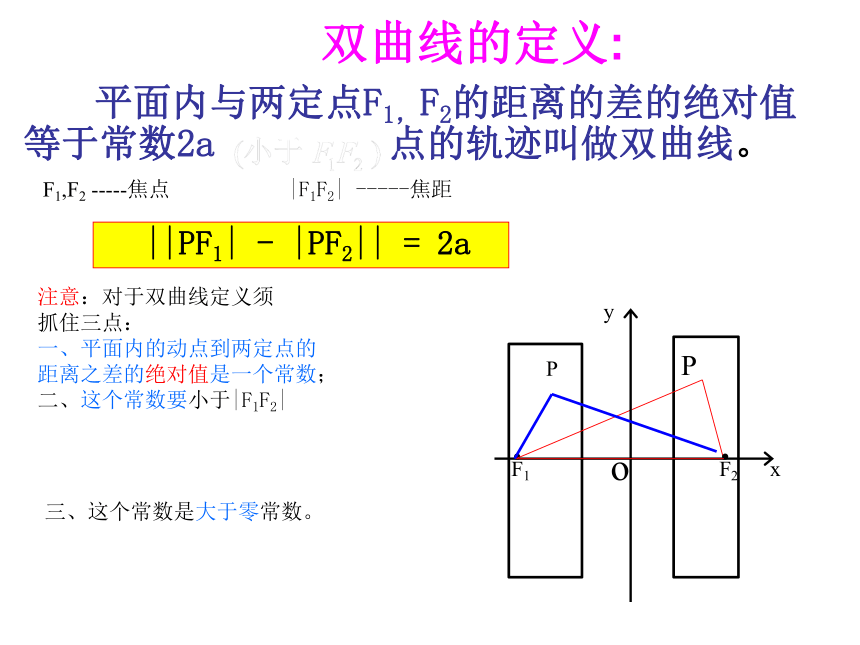
双曲线的定义:
平面内与两定点F1,F2的距离的差的绝对值等于常数2a 点的轨迹叫做双曲线。
F1,F2 -----焦点
||PF1| - |PF2|| = 2a
|F1F2| -----焦距
.
F2
.
F1
P
y
o
x
注意:对于双曲线定义须
抓住三点:
一、平面内的动点到两定点的
距离之差的绝对值是一个常数;
二、这个常数要小于|F1F2|
P
三、这个常数是大于零常数。
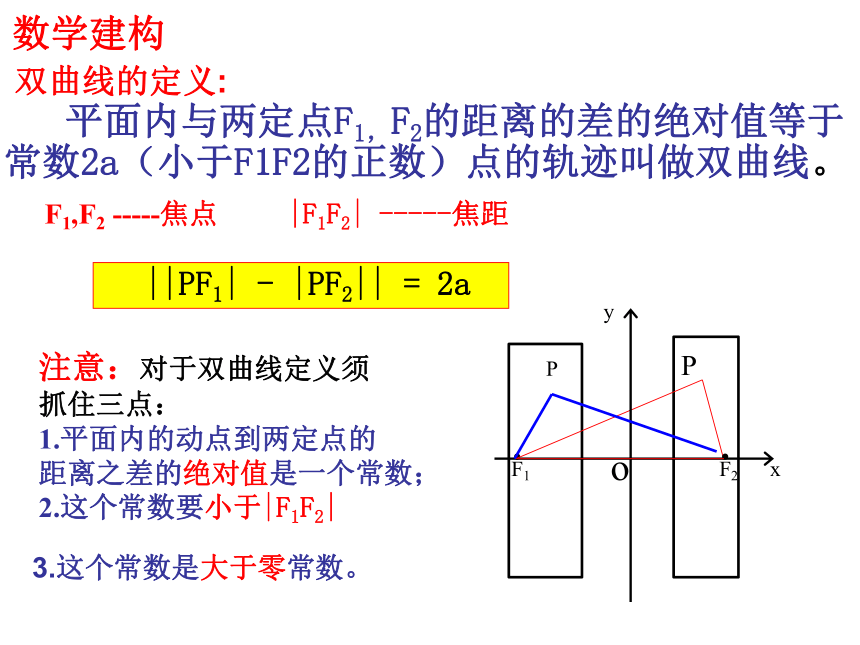
平面内与两定点F1,F2的距离的差的绝对值等于常数2a(小于F1F2的正数)点的轨迹叫做双曲线。
F1,F2 -----焦点
||PF1| - |PF2|| = 2a
|F1F2| -----焦距
.
F2
.
F1
P
y
o
x
注意:对于双曲线定义须
抓住三点:
1.平面内的动点到两定点的
距离之差的绝对值是一个常数;
2.这个常数要小于|F1F2|
P
3.这个常数是大于零常数。
数学建构
双曲线的定义:
数学建构
(1) 如何建立坐标系?
(3) 如何用代数式表示这个几何条件?
(4) 如何化简这个代数式?令c2-a2=b2(b>0),双曲线的
方程可化为什么形式?
以 所在的直线为 轴,线段 的垂直平分线为 轴,建立直角坐标系
则 的坐标分别是
设点
列等式
代入
化简
建系
双曲线的标准方程推导:
数学建构
数学建构
双曲线的标准方程推导:
思考:双曲线的标准方程有什么结构特征?
数学建构
思考:两种形式双曲线的标准方程有哪些相同点?
有哪些不同点?如何区分?
数学建构
数学运用
数学运用
数学运用
牛刀小试
数学运用
数学运用
变式练习
数学运用
变式练习
小结:
(3)双曲线方程的焦点位置的判定及a、b、c的
关系的灵活应用
3.2 双曲线?
3.2.1双曲线的标准方程(1)?
创设情境
发电厂冷却塔轴截面的外轮廓线的形状是双曲线.用点光源照射一个放在地面上的球,适当调整点光源的位置,球在地面上影子的外轮廓线可以是双曲线的一部分.
数 学 实 验
[1]取一条拉链;
[2]如图把它固定在板上的两点F1、F2;
[3] 拉动拉链(M)
思考:拉链运动的轨迹是什么?
小组合作:
双曲线的定义:
平面内与两定点F1,F2的距离的差的绝对值等于常数2a 点的轨迹叫做双曲线。
F1,F2 -----焦点
||PF1| - |PF2|| = 2a
|F1F2| -----焦距
.
F2
.
F1
P
y
o
x
注意:对于双曲线定义须
抓住三点:
一、平面内的动点到两定点的
距离之差的绝对值是一个常数;
二、这个常数要小于|F1F2|
P
三、这个常数是大于零常数。
平面内与两定点F1,F2的距离的差的绝对值等于常数2a(小于F1F2的正数)点的轨迹叫做双曲线。
F1,F2 -----焦点
||PF1| - |PF2|| = 2a
|F1F2| -----焦距
.
F2
.
F1
P
y
o
x
注意:对于双曲线定义须
抓住三点:
1.平面内的动点到两定点的
距离之差的绝对值是一个常数;
2.这个常数要小于|F1F2|
P
3.这个常数是大于零常数。
数学建构
双曲线的定义:
数学建构
(1) 如何建立坐标系?
(3) 如何用代数式表示这个几何条件?
(4) 如何化简这个代数式?令c2-a2=b2(b>0),双曲线的
方程可化为什么形式?
以 所在的直线为 轴,线段 的垂直平分线为 轴,建立直角坐标系
则 的坐标分别是
设点
列等式
代入
化简
建系
双曲线的标准方程推导:
数学建构
数学建构
双曲线的标准方程推导:
思考:双曲线的标准方程有什么结构特征?
数学建构
思考:两种形式双曲线的标准方程有哪些相同点?
有哪些不同点?如何区分?
数学建构
数学运用
数学运用
数学运用
牛刀小试
数学运用
数学运用
变式练习
数学运用
变式练习
小结:
(3)双曲线方程的焦点位置的判定及a、b、c的
关系的灵活应用
