1.2空间向量在立体几何中的应用 同步练习-2021-2022学年高二上学期数学人教B版(2019)选择性必修第一册(Word含答案)
文档属性
| 名称 | 1.2空间向量在立体几何中的应用 同步练习-2021-2022学年高二上学期数学人教B版(2019)选择性必修第一册(Word含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 390.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-06 08:56:40 | ||
图片预览



文档简介
1.2空间向量在立体几何中的应用
一、选择题(共13题)
若二面角 为 ,,,直线 , 所成的角为 ,则 的取值范围是
A. B. C. D.
在二面角 的棱 上任选一点 ,若 是二面角 的平面角,则必须具有的条件是
A. ,,
B. ,
C. ,,
D. ,,且 ,
若直线 的方向向量为 ,平面 的法向量为 ,则可能使 的是
A. ,
B. ,
C. ,
D. ,
如图,在等腰 中,,, 为 的中点, 为 的中点, 为线段 上一个动点(异于两端点), 沿 翻折至 ,点 在平面 上的投影为点 ,当点 在线段 上运动时,以下说法错误的是
A.线段 为定长 B.
C. D.点 的轨迹是圆弧
设点 , 分别是正方体 的棱 和 的中点,在正方体的十二条面对角线中,与截面 成 角的对角线的条数是
A. B. C. D.
若两条不重合直线 和 的方向向量分别为 ,,则直线 和 的位置关系是
A.平行 B.相交 C.垂直 D.不确定
在三棱锥 中,二面角 , 和 的大小均等于 ,,设三棱锥 外接球的球心为 ,直线 与平面 交于点 ,则
A. B. C. D.
已知 是各条棱长均等于 的正三棱柱, 是侧棱 的中点,点 到平面 的距离
A. B. C. D.
在空间直角坐标系 中,四面体 的顶点坐标分别是 ,,,,则点 到平面 的距离是
A. B. C. D.
在长方体 中,,,则 与平面 所成的角的正弦值为
A. B. C. D.
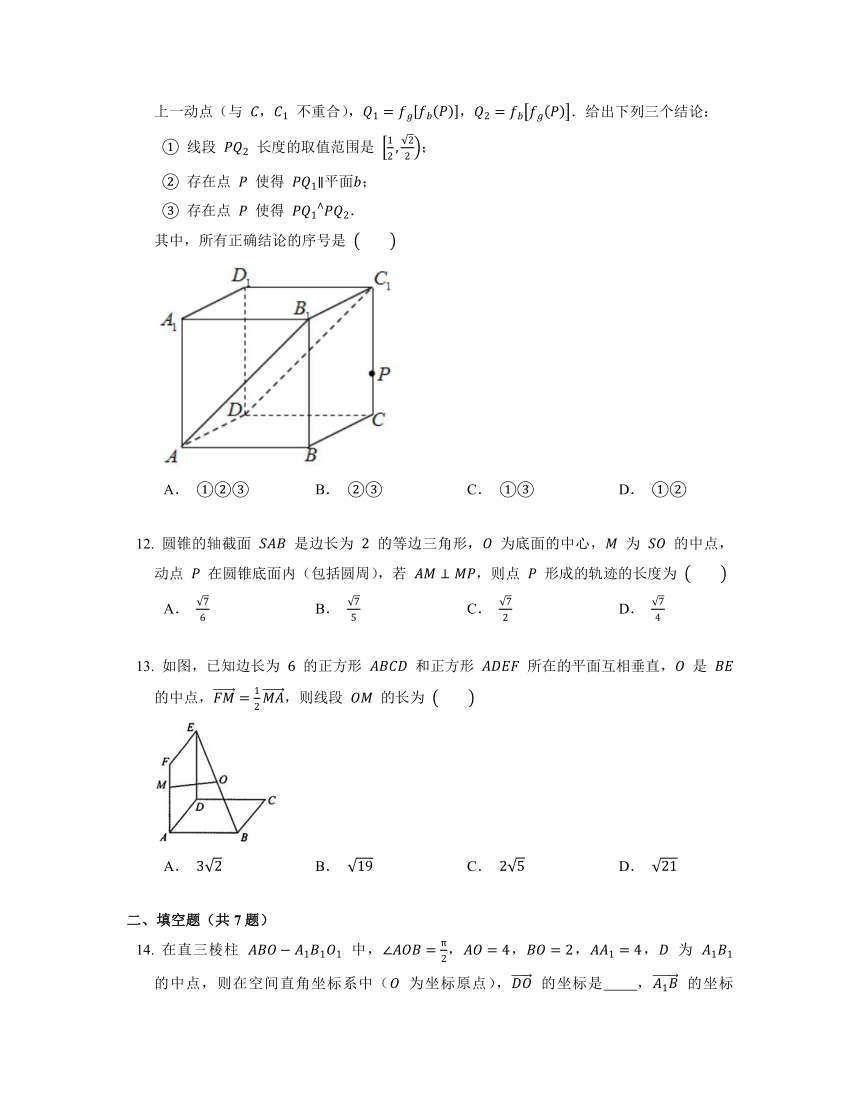
若点 为点 在平面 上的正投影,则记 .如图,在棱长为 的正方体 中,记平面 为 ,平面 为 ,点 是棱 上一动点(与 , 不重合),,.给出下列三个结论:
线段 长度的取值范围是 ;
存在点 使得 ;
存在点 使得 .
其中,所有正确结论的序号是
A. B. C. D.
圆锥的轴截面 是边长为 的等边三角形, 为底面的中心, 为 的中点,动点 在圆锥底面内(包括圆周),若 ,则点 形成的轨迹的长度为
A. B. C. D.
如图,已知边长为 的正方形 和正方形 所在的平面互相垂直, 是 的中点,,则线段 的长为
A. B. C. D.
二、填空题(共7题)
在直三棱柱 中,,,,, 为 的中点,则在空间直角坐标系中( 为坐标原点), 的坐标是 , 的坐标是 .
在正四棱锥 中,若侧面与底面所成二面角的大小为 ,则异面直线 与 所成角的大小等于 .(结果用反三角函数值表示)
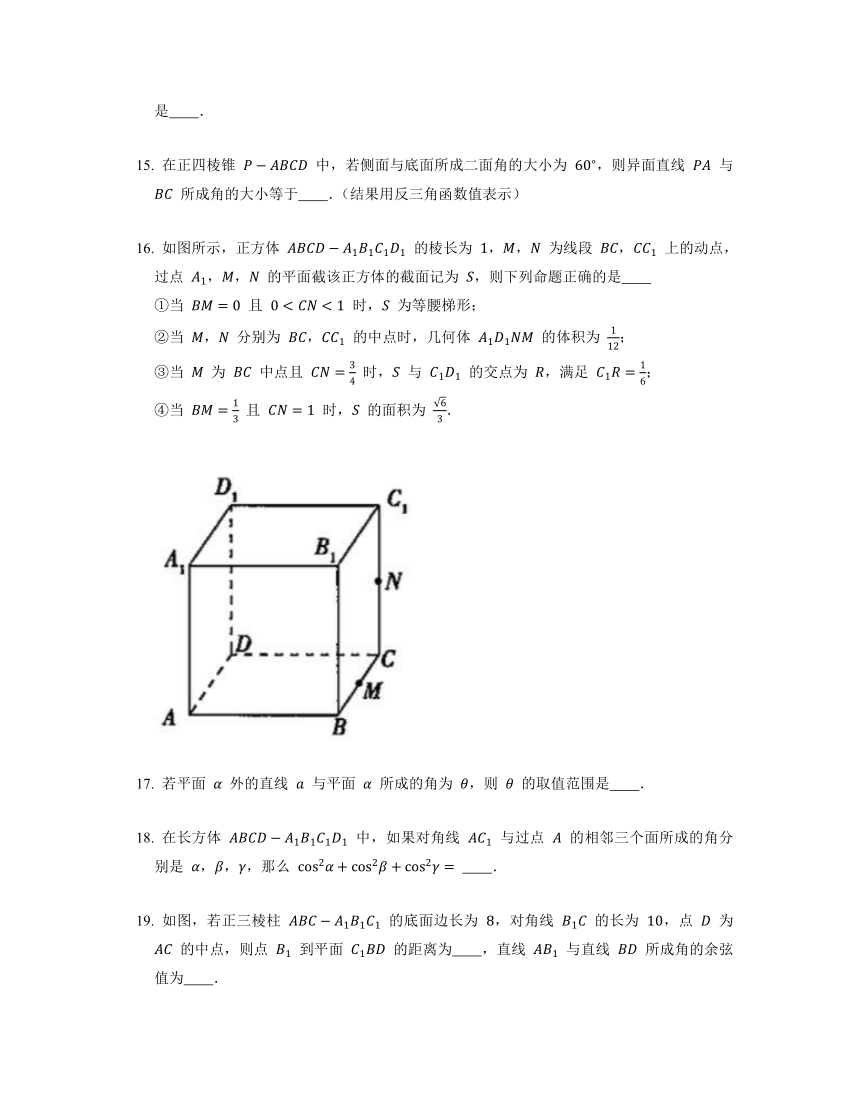
如图所示,正方体 的棱长为 ,, 为线段 , 上的动点,过点 ,, 的平面截该正方体的截面记为 ,则下列命题正确的是
①当 且 时, 为等腰梯形;
②当 , 分别为 , 的中点时,几何体 的体积为 ;
③当 为 中点且 时, 与 的交点为 ,满足 ;
④当 且 时, 的面积为 .
若平面 外的直线 与平面 所成的角为 ,则 的取值范围是 .
在长方体 中,如果对角线 与过点 的相邻三个面所成的角分别是 ,,,那么 .
如图,若正三棱柱 的底面边长为 ,对角线 的长为 ,点 为 的中点,则点 到平面 的距离为 ,直线 与直线 所成角的余弦值为 .
棱长相等的三棱锥的任意两个面组成的二面角的余弦值是 .
三、解答题(共5题)
已知空间四边形 的四个顶点为 ,,,,求证:对边的中点连线互相平分.
在正三角形 中,,, 分别是 ,, 边上的点,满足 (如图1).将 沿 折起到 的位置,使二面角 成直二面角,连接 ,(如图2).
(1) 求证:;
(2) 求直线 与平面 所成角的大小;
(3) 求二面角 的余弦值.
如图,在三棱锥 中,,,.
(1) 求证:;
(2) 若二面角 的大小为 ,且 ,求 的中线 与平面 所成角的正弦值.
如图,已知长方形 中,,, 为 的中点.将 沿 折起,使得 .
(1) 求证:;
(2) 若点 是线段 上的一动点,问点 在何位置时,二面角 的余弦值为 .
如图,四边形 为梯形,四边形 为矩形,,,, 为 的中点.
(1) 证明:.
(2) 求平面 与平面 的夹角的大小.
答案解析
一、选择题(共13题)
1. 【答案】B
【解析】由二面角 的大小为 ,,
得直线 与平面 所成角的大小为 ,
所以平面 内的直线与直线 所成角的最小值为 ,而最大值为 .
2. 【答案】D
3. 【答案】D
【解析】直线 的方向向量为 ,平面 的法向量为 ,要使 ,只需 即可.四个选项中,只有D选项满足 .
4. 【答案】C
【解析】如图,记 为 在平面 上的射影,
由 可得 .
记 交 于点 ,则 .
在 中,作 交 于点 ,连接 ,
则 ,,从而点 在平面 上的射影 在直线 上.
取 的中点 ,则 ,, 均为定长.
易知点 的轨迹是以点 为圆心、 为半径的圆弧,
因为 ,且 ,
所以 .
又 ,,
所以 ,得 ,于是 .
故选C.
5. 【答案】C
6. 【答案】A
【解析】因为两条不重合直线 和 的方向向量分别为 ,,
所以 ,即 与 共线,
所以两条不重合直线 和 的位置关系是平行.
7. 【答案】D
【解析】依题意,如图①,
易知点 在平面 内的射影为三角形 内切圆的圆心 ,
设内切圆的半径为 ,则 ,解得 ,
又二面角 , 和 的大小均等于 ,
所以 .
设 的外接圆圆心为 ,易知 ,
又 ,
所以 ,
故点 ,,, 四点共面,且 ,
又 在平面 内,且 在平面 内,
所以 在 上,即 ,, 三点共线.
现在研究 的长度,过 作 ,交 的延长线于 ,如图②,
在图①中,易知 ,,
故 ,显然 ,
设 ,由 ,即 ,得 ,
解得 ,
所以 ,
所以 .
8. 【答案】A
【解析】以 为原点,以垂直 的直线为 轴,以 为 轴,以 为 轴,建立空间直角坐标系,
因为 是各条棱长均等于 的正三棱柱, 是侧棱 的中点,
所以 ,,,,
所以 ,,,
设平面 的法向量 ,
因为 ,,
所以
所以 ,
所以 到平面 的距离 .
9. 【答案】A
【解析】由题意知 ,,.
设平面 的一个法向量为 ,则 取 ,则 ,,
所以 ,
所以 ,即点 到平面 的距离是 .
10. 【答案】B
【解析】如图所示,作 ,于点 ,连接 ,
因为 ,,
所以 .
又因为 ,,
所以 ,
所以 与平面 所成的角为 ,
在 中,,,
由等面积法得到 ,,
所以 的正弦值为 .
11. 【答案】D
12. 【答案】C
【解析】以底面中心 为原点,建立如图所示的空间直角坐标系,
则 ,,,,
设 ,其中 ,,
则 ,,
因为 ,
所以 ,
所以 ,故点 形成的轨迹方程为 ,故点 形成的轨迹长度为 .
13. 【答案】B
【解析】由题意可建立以 为坐标原点,,, 所在直线分别为 轴、 轴、 轴的空间直角坐标系(图略),则 ,,,,
所以 ,即线段 的长为 .
二、填空题(共7题)
14. 【答案】 ;
【解析】如图建系,
则 ,,,,
所以 ,
因为 为 的中点,
所以 ,
所以 .
15. 【答案】
16. 【答案】①②
【解析】①如图 所示,连接 ,过 作 交 于 ,连接 ,,,则截面为四边形 ,
因为 ,
所以 ,易知 ,
所以 ,所以截面为等腰梯形.故①正确.
②以 为原点,,, 所在直线分别为 轴, 轴, 轴,建立空间直角坐标系,如图 所示,
则 ,,,,
所以 ,,,
设平面 的法向量为 ,则
取 ,则法向量 .
所以点 到平面 的距离 ,
因为 ,所以 ,
所以 .
故②正确.
③延长 交 的延长线于一点 ,连接 交 于点 ,连接 ,,如图 所示,
因为 ,所以 ,所以 ,
因为 ,所以 ,所以 .故③错误.
④连接 ,,延长 交 的延长线于 ,连接 交 于 ,连接 ,,则截面为四边形 ,如图 所示,
易知 ,所以 .
所以 ,
所以 .
在 中,,,
所以边 上的高为 ,
所以 ,
所以 .故④错误.
17. 【答案】
18. 【答案】
19. 【答案】 ;
【解析】取 中点 ,连接 ,,则 , 和 两两相互垂直,
则如图所示以点 为坐标原点建立空间直角坐标系,
则 ,,,,
,,,
则 ,,,
设平面 的法向量为 ,
则
令 则 ,
所以点 到平面 的距离 ,
因为 ,,
所以 ,
所以直线 与直线 所成角的余弦值为 .
20. 【答案】
【解析】如图,三棱锥 的棱长都相等,取 中点 ,连接 ,,
因为三棱锥 各棱长均相等,
所以 ,,
所以 是二面角 的平面角,
设棱长 ,则 ,
所以 .
即棱长相等的三棱锥的任意两个面组成的二面角的余弦值是 .
三、解答题(共5题)
21. 【答案】设 ,,, 的中点分别为点 ,,,,则 ,,,.
设 , 的中点分别为点 ,,则 ,.
显然, 与 是同一点,即线段 的中点就是线段 的中点.
所以空间四边形 的对边中点连线互相平分.
22. 【答案】
(1) 在图 1 中,取 的中点 ,连接 .
因为 ,所以 ,而 ,所以 是正三角形,
又 ,所以 ,在图2中,,,
所以 为二面角 的平面角.
由题设条件知此二面角为直二面角,所以 .
又 ,所以 ,即 .
(2) 建立分别以 ,, 为 轴, 轴, 轴的空间直角坐标系,
则 ,,,,,则 ,,.
设平面 的法向量 ,
由 知,,,即
令 ,得 ,,.所以直线 与平面 所成的角为 .
(3) ,,设平面 的法向量为 .
由 知,,,即
令 ,得 ,,.所以二面角 的余弦值是 .
23. 【答案】
(1) 取 的中点 ,连接 ,.
因为 ,,
所以 ,.
又 ,,且 ,
所以 .
又 ,
所以 .
(2) 由()易知 是二面角 的平面角,
所以 ,
又 ,
所以 ,
在平面 内作 ,则 ,
可建立如图所示的空间直角坐标系,
易得 ,故在 中,
由余弦定理可得 ,
所以 ,,,.
又因为 为 的中点,
所以 ,
所以 .
又平面 的一个法向量为 ,
所以直线 与平面 所成角的正弦值 .
24. 【答案】
(1) 因为长方形 中,,, 为 的中点,
所以 ,,
所以
因为 ,,,
所以 ,
因为 ,
所以 .
(2) 以 的中点 为原点,建立如图所示的空间直角坐标系,则 ,,,,
设 ,
则平面 的一个法向量为 ,
,,
设平面 的一个法向量为 ,
则
即
取 ,得 ,,所以 ,
因为 ,解得 ,
所以 为 的中点时,二面角 的余弦值为 .
25. 【答案】
(1) (法 )
连接 与 相交于 ,连接 .
因为四边形 为矩形,
所以 为 中点,
又 为 的中点,
所以,在 中,.
.
(法 )
因为四边形 为矩形,且 为 的中点,
所以 .
从而 与 , 是共面向量.
又 ,
所以 .
(2) 因为四边形 为矩形,
所以 .
又 ,,,
所以 ,
而 ,
所以,以 为原点, 为 轴, 为 轴, 为 轴,建立空间直角坐标系 ,如图.
设 ,由已知,得 ,,,.
设平面 的一个法向量为 ,则 ,且 ,
所以 ,且 ,
即 取 ,得 ,
,即 .
同理,可求得平面 的一个法向量为 .
.
所以,平面 与平面 的夹角为 .
一、选择题(共13题)
若二面角 为 ,,,直线 , 所成的角为 ,则 的取值范围是
A. B. C. D.
在二面角 的棱 上任选一点 ,若 是二面角 的平面角,则必须具有的条件是
A. ,,
B. ,
C. ,,
D. ,,且 ,
若直线 的方向向量为 ,平面 的法向量为 ,则可能使 的是
A. ,
B. ,
C. ,
D. ,
如图,在等腰 中,,, 为 的中点, 为 的中点, 为线段 上一个动点(异于两端点), 沿 翻折至 ,点 在平面 上的投影为点 ,当点 在线段 上运动时,以下说法错误的是
A.线段 为定长 B.
C. D.点 的轨迹是圆弧
设点 , 分别是正方体 的棱 和 的中点,在正方体的十二条面对角线中,与截面 成 角的对角线的条数是
A. B. C. D.
若两条不重合直线 和 的方向向量分别为 ,,则直线 和 的位置关系是
A.平行 B.相交 C.垂直 D.不确定
在三棱锥 中,二面角 , 和 的大小均等于 ,,设三棱锥 外接球的球心为 ,直线 与平面 交于点 ,则
A. B. C. D.
已知 是各条棱长均等于 的正三棱柱, 是侧棱 的中点,点 到平面 的距离
A. B. C. D.
在空间直角坐标系 中,四面体 的顶点坐标分别是 ,,,,则点 到平面 的距离是
A. B. C. D.
在长方体 中,,,则 与平面 所成的角的正弦值为
A. B. C. D.
若点 为点 在平面 上的正投影,则记 .如图,在棱长为 的正方体 中,记平面 为 ,平面 为 ,点 是棱 上一动点(与 , 不重合),,.给出下列三个结论:
线段 长度的取值范围是 ;
存在点 使得 ;
存在点 使得 .
其中,所有正确结论的序号是
A. B. C. D.
圆锥的轴截面 是边长为 的等边三角形, 为底面的中心, 为 的中点,动点 在圆锥底面内(包括圆周),若 ,则点 形成的轨迹的长度为
A. B. C. D.
如图,已知边长为 的正方形 和正方形 所在的平面互相垂直, 是 的中点,,则线段 的长为
A. B. C. D.
二、填空题(共7题)
在直三棱柱 中,,,,, 为 的中点,则在空间直角坐标系中( 为坐标原点), 的坐标是 , 的坐标是 .
在正四棱锥 中,若侧面与底面所成二面角的大小为 ,则异面直线 与 所成角的大小等于 .(结果用反三角函数值表示)
如图所示,正方体 的棱长为 ,, 为线段 , 上的动点,过点 ,, 的平面截该正方体的截面记为 ,则下列命题正确的是
①当 且 时, 为等腰梯形;
②当 , 分别为 , 的中点时,几何体 的体积为 ;
③当 为 中点且 时, 与 的交点为 ,满足 ;
④当 且 时, 的面积为 .
若平面 外的直线 与平面 所成的角为 ,则 的取值范围是 .
在长方体 中,如果对角线 与过点 的相邻三个面所成的角分别是 ,,,那么 .
如图,若正三棱柱 的底面边长为 ,对角线 的长为 ,点 为 的中点,则点 到平面 的距离为 ,直线 与直线 所成角的余弦值为 .
棱长相等的三棱锥的任意两个面组成的二面角的余弦值是 .
三、解答题(共5题)
已知空间四边形 的四个顶点为 ,,,,求证:对边的中点连线互相平分.
在正三角形 中,,, 分别是 ,, 边上的点,满足 (如图1).将 沿 折起到 的位置,使二面角 成直二面角,连接 ,(如图2).
(1) 求证:;
(2) 求直线 与平面 所成角的大小;
(3) 求二面角 的余弦值.
如图,在三棱锥 中,,,.
(1) 求证:;
(2) 若二面角 的大小为 ,且 ,求 的中线 与平面 所成角的正弦值.
如图,已知长方形 中,,, 为 的中点.将 沿 折起,使得 .
(1) 求证:;
(2) 若点 是线段 上的一动点,问点 在何位置时,二面角 的余弦值为 .
如图,四边形 为梯形,四边形 为矩形,,,, 为 的中点.
(1) 证明:.
(2) 求平面 与平面 的夹角的大小.
答案解析
一、选择题(共13题)
1. 【答案】B
【解析】由二面角 的大小为 ,,
得直线 与平面 所成角的大小为 ,
所以平面 内的直线与直线 所成角的最小值为 ,而最大值为 .
2. 【答案】D
3. 【答案】D
【解析】直线 的方向向量为 ,平面 的法向量为 ,要使 ,只需 即可.四个选项中,只有D选项满足 .
4. 【答案】C
【解析】如图,记 为 在平面 上的射影,
由 可得 .
记 交 于点 ,则 .
在 中,作 交 于点 ,连接 ,
则 ,,从而点 在平面 上的射影 在直线 上.
取 的中点 ,则 ,, 均为定长.
易知点 的轨迹是以点 为圆心、 为半径的圆弧,
因为 ,且 ,
所以 .
又 ,,
所以 ,得 ,于是 .
故选C.
5. 【答案】C
6. 【答案】A
【解析】因为两条不重合直线 和 的方向向量分别为 ,,
所以 ,即 与 共线,
所以两条不重合直线 和 的位置关系是平行.
7. 【答案】D
【解析】依题意,如图①,
易知点 在平面 内的射影为三角形 内切圆的圆心 ,
设内切圆的半径为 ,则 ,解得 ,
又二面角 , 和 的大小均等于 ,
所以 .
设 的外接圆圆心为 ,易知 ,
又 ,
所以 ,
故点 ,,, 四点共面,且 ,
又 在平面 内,且 在平面 内,
所以 在 上,即 ,, 三点共线.
现在研究 的长度,过 作 ,交 的延长线于 ,如图②,
在图①中,易知 ,,
故 ,显然 ,
设 ,由 ,即 ,得 ,
解得 ,
所以 ,
所以 .
8. 【答案】A
【解析】以 为原点,以垂直 的直线为 轴,以 为 轴,以 为 轴,建立空间直角坐标系,
因为 是各条棱长均等于 的正三棱柱, 是侧棱 的中点,
所以 ,,,,
所以 ,,,
设平面 的法向量 ,
因为 ,,
所以
所以 ,
所以 到平面 的距离 .
9. 【答案】A
【解析】由题意知 ,,.
设平面 的一个法向量为 ,则 取 ,则 ,,
所以 ,
所以 ,即点 到平面 的距离是 .
10. 【答案】B
【解析】如图所示,作 ,于点 ,连接 ,
因为 ,,
所以 .
又因为 ,,
所以 ,
所以 与平面 所成的角为 ,
在 中,,,
由等面积法得到 ,,
所以 的正弦值为 .
11. 【答案】D
12. 【答案】C
【解析】以底面中心 为原点,建立如图所示的空间直角坐标系,
则 ,,,,
设 ,其中 ,,
则 ,,
因为 ,
所以 ,
所以 ,故点 形成的轨迹方程为 ,故点 形成的轨迹长度为 .
13. 【答案】B
【解析】由题意可建立以 为坐标原点,,, 所在直线分别为 轴、 轴、 轴的空间直角坐标系(图略),则 ,,,,
所以 ,即线段 的长为 .
二、填空题(共7题)
14. 【答案】 ;
【解析】如图建系,
则 ,,,,
所以 ,
因为 为 的中点,
所以 ,
所以 .
15. 【答案】
16. 【答案】①②
【解析】①如图 所示,连接 ,过 作 交 于 ,连接 ,,,则截面为四边形 ,
因为 ,
所以 ,易知 ,
所以 ,所以截面为等腰梯形.故①正确.
②以 为原点,,, 所在直线分别为 轴, 轴, 轴,建立空间直角坐标系,如图 所示,
则 ,,,,
所以 ,,,
设平面 的法向量为 ,则
取 ,则法向量 .
所以点 到平面 的距离 ,
因为 ,所以 ,
所以 .
故②正确.
③延长 交 的延长线于一点 ,连接 交 于点 ,连接 ,,如图 所示,
因为 ,所以 ,所以 ,
因为 ,所以 ,所以 .故③错误.
④连接 ,,延长 交 的延长线于 ,连接 交 于 ,连接 ,,则截面为四边形 ,如图 所示,
易知 ,所以 .
所以 ,
所以 .
在 中,,,
所以边 上的高为 ,
所以 ,
所以 .故④错误.
17. 【答案】
18. 【答案】
19. 【答案】 ;
【解析】取 中点 ,连接 ,,则 , 和 两两相互垂直,
则如图所示以点 为坐标原点建立空间直角坐标系,
则 ,,,,
,,,
则 ,,,
设平面 的法向量为 ,
则
令 则 ,
所以点 到平面 的距离 ,
因为 ,,
所以 ,
所以直线 与直线 所成角的余弦值为 .
20. 【答案】
【解析】如图,三棱锥 的棱长都相等,取 中点 ,连接 ,,
因为三棱锥 各棱长均相等,
所以 ,,
所以 是二面角 的平面角,
设棱长 ,则 ,
所以 .
即棱长相等的三棱锥的任意两个面组成的二面角的余弦值是 .
三、解答题(共5题)
21. 【答案】设 ,,, 的中点分别为点 ,,,,则 ,,,.
设 , 的中点分别为点 ,,则 ,.
显然, 与 是同一点,即线段 的中点就是线段 的中点.
所以空间四边形 的对边中点连线互相平分.
22. 【答案】
(1) 在图 1 中,取 的中点 ,连接 .
因为 ,所以 ,而 ,所以 是正三角形,
又 ,所以 ,在图2中,,,
所以 为二面角 的平面角.
由题设条件知此二面角为直二面角,所以 .
又 ,所以 ,即 .
(2) 建立分别以 ,, 为 轴, 轴, 轴的空间直角坐标系,
则 ,,,,,则 ,,.
设平面 的法向量 ,
由 知,,,即
令 ,得 ,,.所以直线 与平面 所成的角为 .
(3) ,,设平面 的法向量为 .
由 知,,,即
令 ,得 ,,.所以二面角 的余弦值是 .
23. 【答案】
(1) 取 的中点 ,连接 ,.
因为 ,,
所以 ,.
又 ,,且 ,
所以 .
又 ,
所以 .
(2) 由()易知 是二面角 的平面角,
所以 ,
又 ,
所以 ,
在平面 内作 ,则 ,
可建立如图所示的空间直角坐标系,
易得 ,故在 中,
由余弦定理可得 ,
所以 ,,,.
又因为 为 的中点,
所以 ,
所以 .
又平面 的一个法向量为 ,
所以直线 与平面 所成角的正弦值 .
24. 【答案】
(1) 因为长方形 中,,, 为 的中点,
所以 ,,
所以
因为 ,,,
所以 ,
因为 ,
所以 .
(2) 以 的中点 为原点,建立如图所示的空间直角坐标系,则 ,,,,
设 ,
则平面 的一个法向量为 ,
,,
设平面 的一个法向量为 ,
则
即
取 ,得 ,,所以 ,
因为 ,解得 ,
所以 为 的中点时,二面角 的余弦值为 .
25. 【答案】
(1) (法 )
连接 与 相交于 ,连接 .
因为四边形 为矩形,
所以 为 中点,
又 为 的中点,
所以,在 中,.
.
(法 )
因为四边形 为矩形,且 为 的中点,
所以 .
从而 与 , 是共面向量.
又 ,
所以 .
(2) 因为四边形 为矩形,
所以 .
又 ,,,
所以 ,
而 ,
所以,以 为原点, 为 轴, 为 轴, 为 轴,建立空间直角坐标系 ,如图.
设 ,由已知,得 ,,,.
设平面 的一个法向量为 ,则 ,且 ,
所以 ,且 ,
即 取 ,得 ,
,即 .
同理,可求得平面 的一个法向量为 .
.
所以,平面 与平面 的夹角为 .
