2021-2022学年湖南省永州市道县九年级(上)期中数学试卷(Word版 含解析)
文档属性
| 名称 | 2021-2022学年湖南省永州市道县九年级(上)期中数学试卷(Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 586.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-02 08:58:38 | ||
图片预览


文档简介
2021-2022学年湖南省永州市道县九年级第一学期期中数学试卷
一、选择题(本大题共10小题,每小题4分,共40分)
1.已知点A(1,2021)在反比例函数的图象上,则k的值是( )
A.2021 B.﹣2021 C.1 D.﹣1
2.方程x2=5x的解是( )
A.x1=﹣5,x2=0 B.x1=5,x2=0 C.x=5 D.x=0
3.已知=,则下列式子成立的是( )
A.3x=5y B.xy=15 C. D.
4.对于反比例函数,下列说法不正确的是( )
A.图象分布在二、四象限内
B.图象经过点(1,﹣2021)
C.当x>0时,y随x的增大而增大
D.若点A(x1,y1),B(x2,y2)都在函数的图象上,且x1<x2时,则y1<y2
5.下列图形中一定是相似形的是( )
A.两个等边三角形 B.两个菱形
C.两个矩形 D.两个直角三角形
6.若方程(x﹣2)2=k可以用直接开平方法解,则k的取值范围是( )
A.k≤0 B.k≥0 C.k<0 D.k≠0
7.已知点A(﹣1,a)与点B(2,b)都在反比例函数的图象上,则a与b之间的关系是( )
A.a>b B.a<b C.a≥b D.a=b
8.关于x的一元二次方程(a﹣1)x2﹣2x+3=0有实数根,则整数a的最大值是( )
A.2 B.1 C.0 D.﹣1
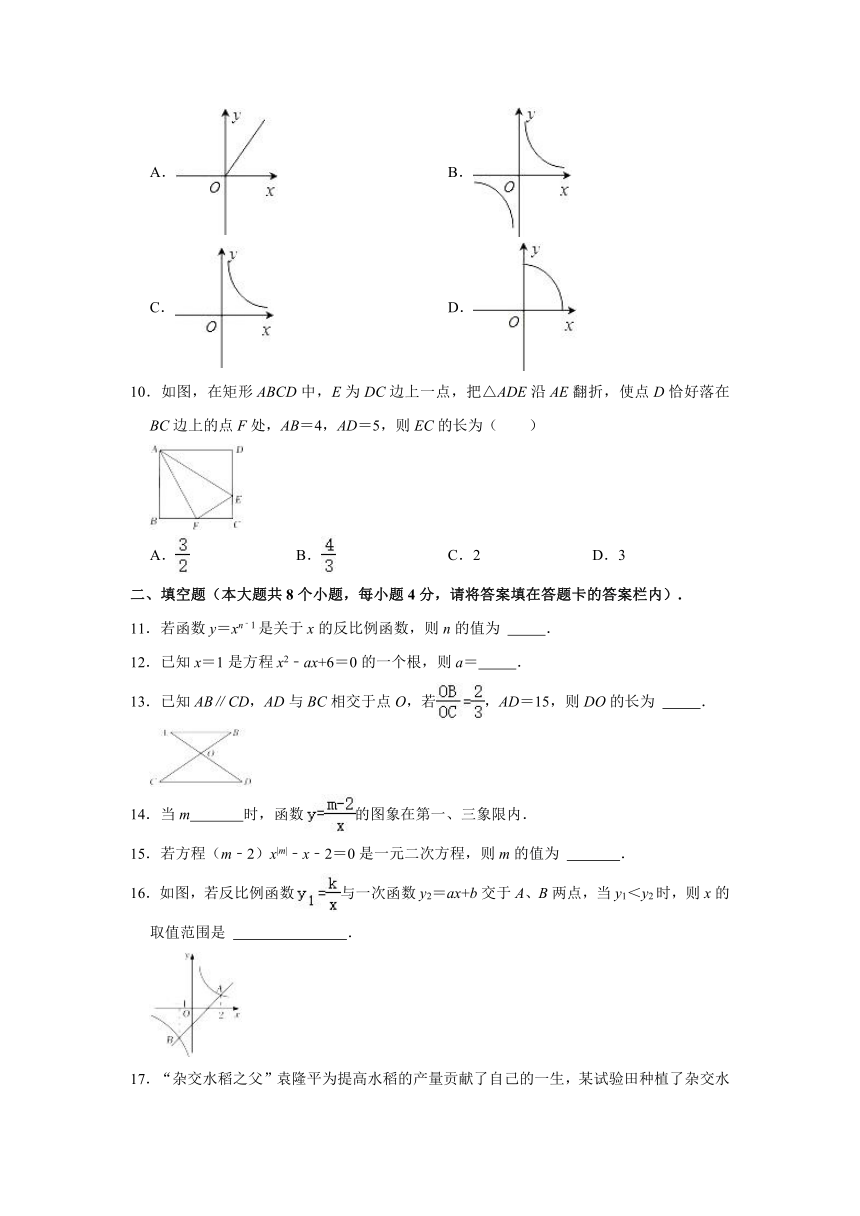
9.一个直角三角形的两直角边长分别为x,y,其面积为3,则y与x之间的关系用图象表示大致为( )
A. B.
C. D.
10.如图,在矩形ABCD中,E为DC边上一点,把△ADE沿AE翻折,使点D恰好落在BC边上的点F处,AB=4,AD=5,则EC的长为( )
A. B. C.2 D.3
二、填空题(本大题共8个小题,每小题4分,请将答案填在答题卡的答案栏内).
11.若函数y=xn﹣1是关于x的反比例函数,则n的值为 .
12.已知x=1是方程x2﹣ax+6=0的一个根,则a= .
13.已知AB∥CD,AD与BC相交于点O,若,AD=15,则DO的长为 .
14.当m 时,函数的图象在第一、三象限内.
15.若方程(m﹣2)x|m|﹣x﹣2=0是一元二次方程,则m的值为 .
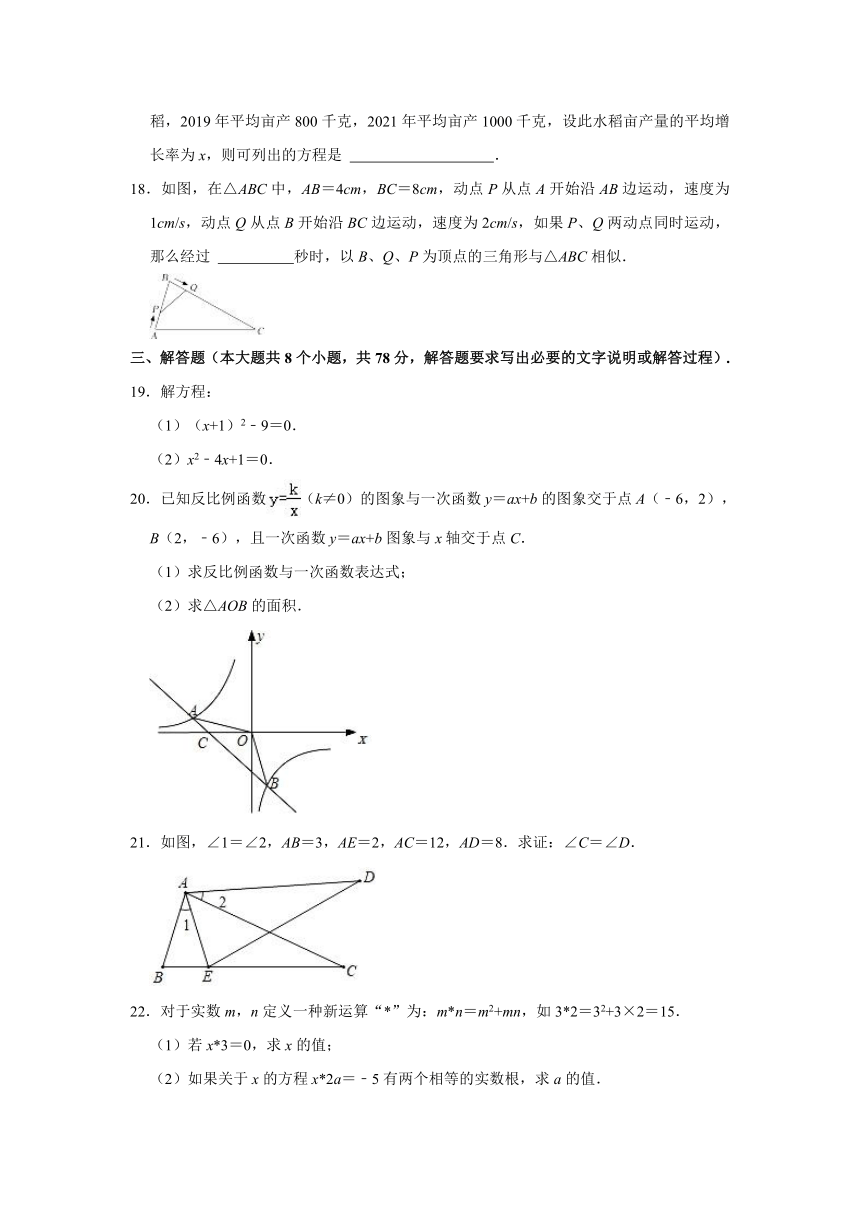
16.如图,若反比例函数与一次函数y2=ax+b交于A、B两点,当y1<y2时,则x的取值范围是 .
17.“杂交水稻之父”袁隆平为提高水稻的产量贡献了自己的一生,某试验田种植了杂交水稻,2019年平均亩产800千克,2021年平均亩产1000千克,设此水稻亩产量的平均增长率为x,则可列出的方程是 .
18.如图,在△ABC中,AB=4cm,BC=8cm,动点P从点A开始沿AB边运动,速度为1cm/s,动点Q从点B开始沿BC边运动,速度为2cm/s,如果P、Q两动点同时运动,那么经过 秒时,以B、Q、P为顶点的三角形与△ABC相似.
三、解答题(本大题共8个小题,共78分,解答题要求写出必要的文字说明或解答过程).
19.解方程:
(1)(x+1)2﹣9=0.
(2)x2﹣4x+1=0.
20.已知反比例函数(k≠0)的图象与一次函数y=ax+b的图象交于点A(﹣6,2),B(2,﹣6),且一次函数y=ax+b图象与x轴交于点C.
(1)求反比例函数与一次函数表达式;
(2)求△AOB的面积.
21.如图,∠1=∠2,AB=3,AE=2,AC=12,AD=8.求证:∠C=∠D.
22.对于实数m,n定义一种新运算“*”为:m*n=m2+mn,如3*2=32+3×2=15.
(1)若x*3=0,求x的值;
(2)如果关于x的方程x*2a=﹣5有两个相等的实数根,求a的值.
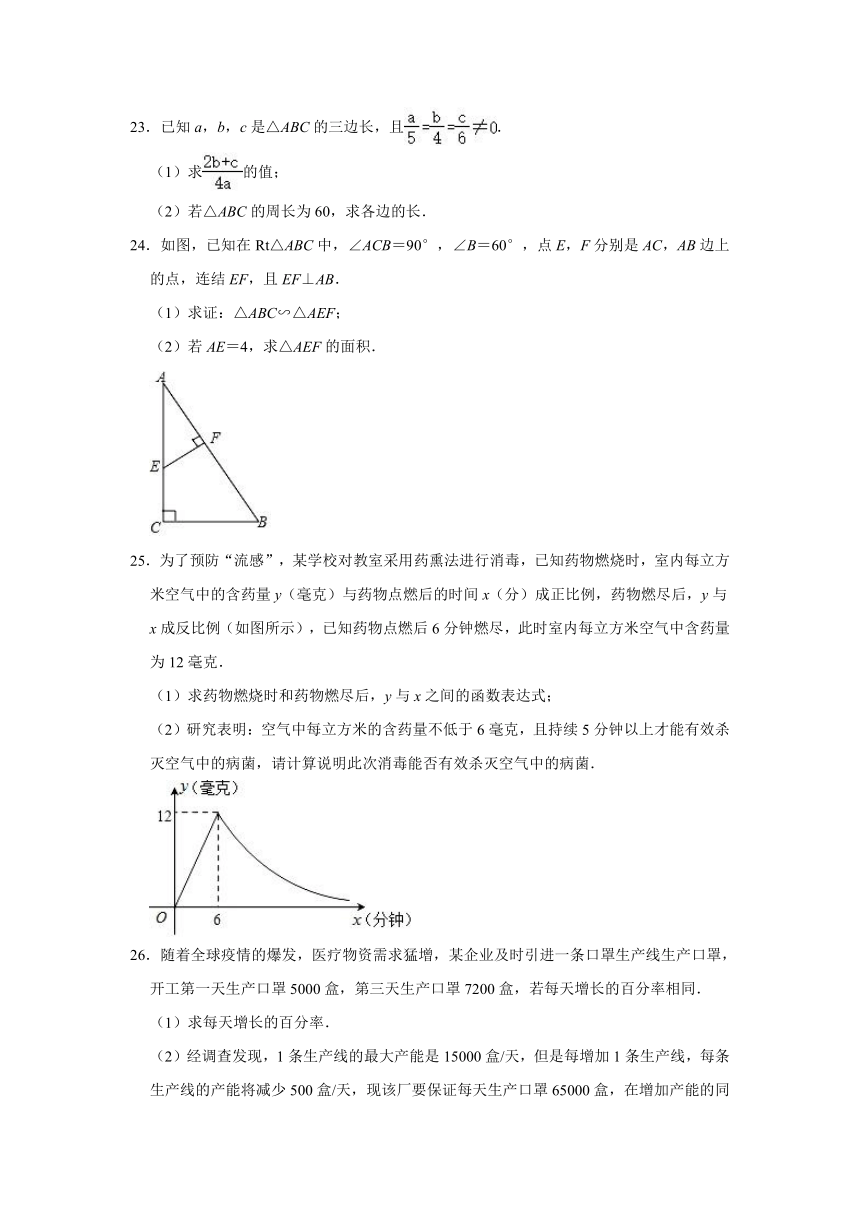
23.已知a,b,c是△ABC的三边长,且.
(1)求的值;
(2)若△ABC的周长为60,求各边的长.
24.如图,已知在Rt△ABC中,∠ACB=90°,∠B=60°,点E,F分别是AC,AB边上的点,连结EF,且EF⊥AB.
(1)求证:△ABC∽△AEF;
(2)若AE=4,求△AEF的面积.
25.为了预防“流感”,某学校对教室采用药熏法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(毫克)与药物点燃后的时间x(分)成正比例,药物燃尽后,y与x成反比例(如图所示),已知药物点燃后6分钟燃尽,此时室内每立方米空气中含药量为12毫克.
(1)求药物燃烧时和药物燃尽后,y与x之间的函数表达式;
(2)研究表明:空气中每立方米的含药量不低于6毫克,且持续5分钟以上才能有效杀灭空气中的病菌,请计算说明此次消毒能否有效杀灭空气中的病菌.
26.随着全球疫情的爆发,医疗物资需求猛增,某企业及时引进一条口罩生产线生产口罩,开工第一天生产口罩5000盒,第三天生产口罩7200盒,若每天增长的百分率相同.
(1)求每天增长的百分率.
(2)经调查发现,1条生产线的最大产能是15000盒/天,但是每增加1条生产线,每条生产线的产能将减少500盒/天,现该厂要保证每天生产口罩65000盒,在增加产能的同时又要节省投入的条件下(生产线越多,投入越大),应该增加几条生产线?
参考答案
一、选择题(本大题共10小题,每小题4分,共40分)
1.已知点A(1,2021)在反比例函数的图象上,则k的值是( )
A.2021 B.﹣2021 C.1 D.﹣1
【分析】根据点A的坐标,利用反比例函数图象上点的坐标特征求出k值,此题得解.
解:∵点A(1,2021)在反比例函数的图象上,
∴k=1×2021=2021.
故选:A.
2.方程x2=5x的解是( )
A.x1=﹣5,x2=0 B.x1=5,x2=0 C.x=5 D.x=0
【分析】先把方程化为一般式,然后利用因式分解法解方程.
解:x2﹣5x=0,
x(x﹣5)=0,
x=0或x﹣5=0,
所以x1=0,x2=5.
故选:B.
3.已知=,则下列式子成立的是( )
A.3x=5y B.xy=15 C. D.
【分析】根据比例的性质逐个判断即可.
解:∵=,
∴两边都乘以5y,得5x=3y,
∵=,
∴两边都乘以3y,得xy=15,
∵=,
∴两边都乘以3x,得3y=5x,
即只有选项D符合题意;选项A、B、C都不符合题意;
故选:D.
4.对于反比例函数,下列说法不正确的是( )
A.图象分布在二、四象限内
B.图象经过点(1,﹣2021)
C.当x>0时,y随x的增大而增大
D.若点A(x1,y1),B(x2,y2)都在函数的图象上,且x1<x2时,则y1<y2
【分析】根据反比例函数图象的性质对各选项分析判断后利用排除法求解.
解:A、∵k=﹣2021<0,∴它的图象在第二、四象限,故本选项正确,不符合题意;
B、∵x=1时,y=﹣=﹣2021,∴点(1,﹣2021)在它的图象上,故本选项正确,不符合题意;
C、∵k=﹣2021<0,∴当x<0时,y随x的增大而增大,故本选项正确,不符合题意;
D、∵k=﹣2021<0,∴在每一个象限内,y随x的增大而增大,
∴当x1<x2<0,则y1<y2,故本选项错误,符合题意,
故选:D.
5.下列图形中一定是相似形的是( )
A.两个等边三角形 B.两个菱形
C.两个矩形 D.两个直角三角形
【分析】如果两个多边形的对应角相等,对应边的比相等,则这两个多边形是相似多边形.
解:∵等边三角形的对应角相等,对应边的比相等,
∴两个等边三角形一定是相似形,
又∵直角三角形,菱形的对应角不一定相等,矩形的边不一定对应成比例,
∴两个直角三角形、两个菱形、两个矩形都不一定是相似形,
故选:A.
6.若方程(x﹣2)2=k可以用直接开平方法解,则k的取值范围是( )
A.k≤0 B.k≥0 C.k<0 D.k≠0
【分析】若方程(x﹣2)2=k可以直接用开平方法解,则k≥0.
解:∵(x﹣2)2≥0,
∴k≥0.
故选:B.
7.已知点A(﹣1,a)与点B(2,b)都在反比例函数的图象上,则a与b之间的关系是( )
A.a>b B.a<b C.a≥b D.a=b
【分析】利用反比例函数的性质即可得出结论.
解:反比例函数中,k=12>0,
∴反比例函数的图象在一、三象限,
∵点A(﹣1,a)与点B(2,b)都在反比例函数的图象上,
∴A(﹣1,a)在第三象限,点B(2,b)在第一象限,
∴a<b,
故选:B.
8.关于x的一元二次方程(a﹣1)x2﹣2x+3=0有实数根,则整数a的最大值是( )
A.2 B.1 C.0 D.﹣1
【分析】根据方程有实数根,得到根的判别式的值大于等于0,且二次项系数不为0,即可求出整数a的最大值.
解:根据题意得:Δ=4﹣12(a﹣1)≥0,且a﹣1≠0,
解得:a≤,a≠1,
则整数a的最大值为0.
故选:C.
9.一个直角三角形的两直角边长分别为x,y,其面积为3,则y与x之间的关系用图象表示大致为( )
A. B.
C. D.
【分析】根据题意有:xy=6;故y与x之间的函数图象为反比例函数,且根据xy实际意义x、y应大于0,其图象在第一象限.
解:由题意得,
∴xy=6,
∴y=(x>0,y>0),
故选:C.
10.如图,在矩形ABCD中,E为DC边上一点,把△ADE沿AE翻折,使点D恰好落在BC边上的点F处,AB=4,AD=5,则EC的长为( )
A. B. C.2 D.3
【分析】先由矩形的性质得到AB=CD=4,AD=BC=5,再由折叠得到AF=AD=5,然后求得BF、CF的值,再设CE=x,则EF=ED=4﹣x,然后利用勾股定理列出方程求解,最后得到EC的长.
解:∵四边形ABCD是,
∴AB=CD=4,AD=BC=5,
由折叠得:AF=AD=5,EF=ED,
∴BF=3,
∴CF=BC﹣BF=5﹣3=2,
设CE=x,则EF=ED=4﹣x,
在Rt△EFC中,EC2+FC2=EF2,
∴x2+22=(4﹣x)2,
解得:x=,
∴EC=.
故选:A.
二、填空题(本大题共8个小题,每小题4分,请将答案填在答题卡的答案栏内).
11.若函数y=xn﹣1是关于x的反比例函数,则n的值为 0 .
【分析】根据反比例函数的定义得出n﹣1=﹣1,再求出n即可.
解:∵函数y=xn﹣1是关于x的反比例函数,
∴n﹣1=﹣1,
解得:n=0,
故答案为:0.
12.已知x=1是方程x2﹣ax+6=0的一个根,则a= 7 .
【分析】根据题意将x=1代入方程中即可求出答案.
解:由题意可知:x=1代入x2﹣ax+6=0
1﹣a+6=0
∴a=7
故答案为:7
13.已知AB∥CD,AD与BC相交于点O,若,AD=15,则DO的长为 9 .
【分析】由AB∥CD得出∠A=∠D,∠B=∠C,得出△AOB∽△DOC,进而得出,再根据,AD=15,即可得出OD的长.
解:∵AB∥CD,
∴∠A=∠D,∠B=∠C,
∴△AOB∽△DOC,
∴,
∵,AD=15,
∴,
∴OD=9,
故答案为:9.
14.当m >2 时,函数的图象在第一、三象限内.
【分析】根据反比例函数的性质得m﹣2>0,然后解不等式即可.
解:根据题意得m﹣2>0,
解得m>2.
故答案为:>2.
15.若方程(m﹣2)x|m|﹣x﹣2=0是一元二次方程,则m的值为 ﹣2 .
【分析】根据一元二次方程的定义得到m﹣2≠0且|m|=2,然后解方程和不等式即可得到满足条件的m的值.
解:∵关于x的方程(m﹣2)x|m|﹣x﹣2=0是一元二次方程,
∴|m|=2,m﹣2≠0,
解得m=﹣2;
故答案为:﹣2.
16.如图,若反比例函数与一次函数y2=ax+b交于A、B两点,当y1<y2时,则x的取值范围是 ﹣1<x<0或x>2 .
【分析】写出反比例函数的图象在一次函数的图象下方的自变量的取值范围即可.
解:观察图象可知,当y1<y2时,则x的取值范围是﹣1<x<0或x>2.
故答案为﹣1<x<0或x>2.
17.“杂交水稻之父”袁隆平为提高水稻的产量贡献了自己的一生,某试验田种植了杂交水稻,2019年平均亩产800千克,2021年平均亩产1000千克,设此水稻亩产量的平均增长率为x,则可列出的方程是 800(1+x)2=1000 .
【分析】设此水稻亩产量的平均增长率为x,根据“2019年平均亩产×(1+增长率)2=2021年平均亩产”即可列出关于x的方程,
解:设此水稻亩产量的平均增长率为x,则可列出的方程是800(1+x)2=1000.
故答案是:800(1+x)2=1000.
18.如图,在△ABC中,AB=4cm,BC=8cm,动点P从点A开始沿AB边运动,速度为1cm/s,动点Q从点B开始沿BC边运动,速度为2cm/s,如果P、Q两动点同时运动,那么经过 2或0.8 秒时,以B、Q、P为顶点的三角形与△ABC相似.
【分析】设经过t秒时,以△QBP与△ABC相似,则AP=t厘米,BP=(4﹣t)厘米,BQ=2t厘米,利用两组对应边的比相等且夹角对应相等的两个三角形相似进行分类讨论,由相似三角形的性质列出方程可求解.
解:设经过t秒时,以△QBP与△ABC相似,则AP=t厘米,BP=(4﹣t)厘米,BQ=2t厘米,
∵∠PBQ=∠ABC,
∴当时,△BPQ∽△BAC,即,解得t=2;
当时,△BPQ∽△BCA,即 ,解得t=0.8;
即经过2秒或0.8秒时,△QBP与△ABC相似.
故答案为2或0.8.
三、解答题(本大题共8个小题,共78分,解答题要求写出必要的文字说明或解答过程).
19.解方程:
(1)(x+1)2﹣9=0.
(2)x2﹣4x+1=0.
【分析】(1)利用直接开平方法求解即可;
(2)将常数项移到方程的右边,两边都加上一次项系数一半的平方配成完全平方式后,再开方即可得.
解:(1)(x+1)2﹣9=0,
(x+1)2=9,
∴x+1=3或x+1=﹣3,
∴x1=2,x2=﹣4;
(2)x2﹣4x+1=0,
x2﹣4x=﹣1,
x2﹣4x+4=3,即(x﹣2)2=3,
∴x﹣2=,
∴.
20.已知反比例函数(k≠0)的图象与一次函数y=ax+b的图象交于点A(﹣6,2),B(2,﹣6),且一次函数y=ax+b图象与x轴交于点C.
(1)求反比例函数与一次函数表达式;
(2)求△AOB的面积.
【分析】(1)根据待定系数法求解即可;
(2)求出C点的坐标,再根据三角形的面积公式求出三角形AOC和三角形BOC的面积,相加即可得出答案.
解:(1)把点A(﹣6,2)代入得,2=,
∴k=﹣12,
∴反比例函数的表达式为;
把点A(﹣6,2),B(2,﹣6)代入y=ax+b得,
解得:,
∴一次函数的表达式为y=﹣x﹣4;
(2)∵直线y=﹣x﹣4与x轴交于点C,
∴C(﹣4,0),
∴OC=4,
∴,
∴△AOB的面积为16.
21.如图,∠1=∠2,AB=3,AE=2,AC=12,AD=8.求证:∠C=∠D.
【分析】由∠1=∠2得出∠BAC=∠EAD,由AB=3,AE=2,AC=12,AD=8得出,进而得出△ABC∽△AED,即可得出∠C=∠D.
【解答】证明:∵∠1=∠2,
∴∠1+∠EAC=∠2+∠EAC,
即∠BAC=∠EAD,
∵AB=3,AE=2,AC=12,AD=8,
∴,,
∴,
∴△ABC∽△AED,
∴∠C=∠D.
22.对于实数m,n定义一种新运算“*”为:m*n=m2+mn,如3*2=32+3×2=15.
(1)若x*3=0,求x的值;
(2)如果关于x的方程x*2a=﹣5有两个相等的实数根,求a的值.
【分析】(1)先根据定义得出方程x2+3x=0,再解方程可求出x;
(2)先根据定义得出方程x2+2ax+5=0,再根据方程有两个相等的实数根即可求出a.
解:(1)∵x*3=0,
∴x2+3x=0,
∴x(x+3)=0,
x1=0,x2=﹣3,
∴x的值为0或﹣3;
(2)∵关于x的方程x*2a=﹣5有两个相等的实数根,
∴x2+2ax+5=0有两个相等的实数根,
∴(2a)2﹣4×1×5=0,
解得a1=,a2=﹣,
∴a的值为±.
23.已知a,b,c是△ABC的三边长,且.
(1)求的值;
(2)若△ABC的周长为60,求各边的长.
【分析】(1)直接设a=5k,b=4k,c=6k,进而代入求出答案;
(2)直接设a=5k,b=4k,c=6k,进而代入求出答案.
解:(1),
∴.
(2)∵△ABC的周长为60,
∴a+b+c=60,
∴5k+4k+6k=60,
∴k=4,
∴a=5k=20,b=4k=16,c=6k=24,
∴三角形的各边的长分别为20,16,24.
24.如图,已知在Rt△ABC中,∠ACB=90°,∠B=60°,点E,F分别是AC,AB边上的点,连结EF,且EF⊥AB.
(1)求证:△ABC∽△AEF;
(2)若AE=4,求△AEF的面积.
【分析】(1)由∠ACB=90°,EF⊥AB得出∠AFE=∠ACB=90°,由∠A是公共角,即可得出△ABC∽△AEF;
(2)利用含30°角的直角三角形的性质求出EF的长度,再由勾股定理得出AF的长度,即可求出△AEF的面积.
【解答】(1)证明:∵∠ACB=90°,EF⊥AB,
∴∠AFE=∠ACB=90°,
∵∠A=∠A,
∴△ABC∽△AEF,
(2)解:∵∠ACB=90°,∠B=60°
∴∠A=30°,
在△AEF中,∠AFE=90°,∠A=30°,AE=4
∴,
∴,
∴S△AEF=.
25.为了预防“流感”,某学校对教室采用药熏法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(毫克)与药物点燃后的时间x(分)成正比例,药物燃尽后,y与x成反比例(如图所示),已知药物点燃后6分钟燃尽,此时室内每立方米空气中含药量为12毫克.
(1)求药物燃烧时和药物燃尽后,y与x之间的函数表达式;
(2)研究表明:空气中每立方米的含药量不低于6毫克,且持续5分钟以上才能有效杀灭空气中的病菌,请计算说明此次消毒能否有效杀灭空气中的病菌.
【分析】(1)正比例函数图象过点(6,12),利用待定系数法可求解析式;反比例函数图象过点(6,12),利用待定系数法可求解析式;
(2)将y=6分别代入两个解析式,可求x的值,即可判断此次消毒能否有效杀灭空气中的病菌.
解:(1)设药物燃烧时,y与x之间函数的表达式为y=mx,
把(6,12)代入得,12=6m,
∴m=2,
∴药物燃烧时的函数表达式为y=2x(0≤x≤6);
设药物燃烧后,y与x之间函数的表达式为,
把(6,12)代入得,k=xy=6×12=72,
∴药物燃烧时的函数表达式为(x≥6);
(2)把y=6代入y=2x得,6=2x,
∴x=3,
把y=6代入得,,
∴x=12,
∵12﹣3=9>5,
∴此次消毒能有效杀灭空气中的病菌.
26.随着全球疫情的爆发,医疗物资需求猛增,某企业及时引进一条口罩生产线生产口罩,开工第一天生产口罩5000盒,第三天生产口罩7200盒,若每天增长的百分率相同.
(1)求每天增长的百分率.
(2)经调查发现,1条生产线的最大产能是15000盒/天,但是每增加1条生产线,每条生产线的产能将减少500盒/天,现该厂要保证每天生产口罩65000盒,在增加产能的同时又要节省投入的条件下(生产线越多,投入越大),应该增加几条生产线?
【分析】(1)设每天增长的百分率为x,利用第三天生产口罩的数量=第一天生产口罩的数量×(1+每天增长的百分率)2,即可得出关于x的一元二次方程,解之取其符合题意的值即可得出每天增长的百分率为20%;
(2)设增加y条生产线,则每条生产线的产量为(15000﹣500y)盒/天,利用生产线条数×每条生产线产能=总生产数,即可得出关于y的一元二次方程,解之即可得出y值,再结合要节省投入,即可得出应该增加4条生产线.
解:(1)设每天增长的百分率为x,
依题意得:5000(1+x)2=7200,
x1=0.2=20%,x2=﹣2.2(不合题意,舍去).
答:每天增长的百分率为20%.
(2)设增加y条生产线,则每条生产线的产量为(15000﹣500y)盒/天,
依题意得:(1+y)(15000﹣500y)=65000,
整理得:y2﹣29y+100=0,
解得:y1=4,y2=25.
又∵要节省投入,
∴y=4.
答:应该增加4条生产线.
一、选择题(本大题共10小题,每小题4分,共40分)
1.已知点A(1,2021)在反比例函数的图象上,则k的值是( )
A.2021 B.﹣2021 C.1 D.﹣1
2.方程x2=5x的解是( )
A.x1=﹣5,x2=0 B.x1=5,x2=0 C.x=5 D.x=0
3.已知=,则下列式子成立的是( )
A.3x=5y B.xy=15 C. D.
4.对于反比例函数,下列说法不正确的是( )
A.图象分布在二、四象限内
B.图象经过点(1,﹣2021)
C.当x>0时,y随x的增大而增大
D.若点A(x1,y1),B(x2,y2)都在函数的图象上,且x1<x2时,则y1<y2
5.下列图形中一定是相似形的是( )
A.两个等边三角形 B.两个菱形
C.两个矩形 D.两个直角三角形
6.若方程(x﹣2)2=k可以用直接开平方法解,则k的取值范围是( )
A.k≤0 B.k≥0 C.k<0 D.k≠0
7.已知点A(﹣1,a)与点B(2,b)都在反比例函数的图象上,则a与b之间的关系是( )
A.a>b B.a<b C.a≥b D.a=b
8.关于x的一元二次方程(a﹣1)x2﹣2x+3=0有实数根,则整数a的最大值是( )
A.2 B.1 C.0 D.﹣1
9.一个直角三角形的两直角边长分别为x,y,其面积为3,则y与x之间的关系用图象表示大致为( )
A. B.
C. D.
10.如图,在矩形ABCD中,E为DC边上一点,把△ADE沿AE翻折,使点D恰好落在BC边上的点F处,AB=4,AD=5,则EC的长为( )
A. B. C.2 D.3
二、填空题(本大题共8个小题,每小题4分,请将答案填在答题卡的答案栏内).
11.若函数y=xn﹣1是关于x的反比例函数,则n的值为 .
12.已知x=1是方程x2﹣ax+6=0的一个根,则a= .
13.已知AB∥CD,AD与BC相交于点O,若,AD=15,则DO的长为 .
14.当m 时,函数的图象在第一、三象限内.
15.若方程(m﹣2)x|m|﹣x﹣2=0是一元二次方程,则m的值为 .
16.如图,若反比例函数与一次函数y2=ax+b交于A、B两点,当y1<y2时,则x的取值范围是 .
17.“杂交水稻之父”袁隆平为提高水稻的产量贡献了自己的一生,某试验田种植了杂交水稻,2019年平均亩产800千克,2021年平均亩产1000千克,设此水稻亩产量的平均增长率为x,则可列出的方程是 .
18.如图,在△ABC中,AB=4cm,BC=8cm,动点P从点A开始沿AB边运动,速度为1cm/s,动点Q从点B开始沿BC边运动,速度为2cm/s,如果P、Q两动点同时运动,那么经过 秒时,以B、Q、P为顶点的三角形与△ABC相似.
三、解答题(本大题共8个小题,共78分,解答题要求写出必要的文字说明或解答过程).
19.解方程:
(1)(x+1)2﹣9=0.
(2)x2﹣4x+1=0.
20.已知反比例函数(k≠0)的图象与一次函数y=ax+b的图象交于点A(﹣6,2),B(2,﹣6),且一次函数y=ax+b图象与x轴交于点C.
(1)求反比例函数与一次函数表达式;
(2)求△AOB的面积.
21.如图,∠1=∠2,AB=3,AE=2,AC=12,AD=8.求证:∠C=∠D.
22.对于实数m,n定义一种新运算“*”为:m*n=m2+mn,如3*2=32+3×2=15.
(1)若x*3=0,求x的值;
(2)如果关于x的方程x*2a=﹣5有两个相等的实数根,求a的值.
23.已知a,b,c是△ABC的三边长,且.
(1)求的值;
(2)若△ABC的周长为60,求各边的长.
24.如图,已知在Rt△ABC中,∠ACB=90°,∠B=60°,点E,F分别是AC,AB边上的点,连结EF,且EF⊥AB.
(1)求证:△ABC∽△AEF;
(2)若AE=4,求△AEF的面积.
25.为了预防“流感”,某学校对教室采用药熏法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(毫克)与药物点燃后的时间x(分)成正比例,药物燃尽后,y与x成反比例(如图所示),已知药物点燃后6分钟燃尽,此时室内每立方米空气中含药量为12毫克.
(1)求药物燃烧时和药物燃尽后,y与x之间的函数表达式;
(2)研究表明:空气中每立方米的含药量不低于6毫克,且持续5分钟以上才能有效杀灭空气中的病菌,请计算说明此次消毒能否有效杀灭空气中的病菌.
26.随着全球疫情的爆发,医疗物资需求猛增,某企业及时引进一条口罩生产线生产口罩,开工第一天生产口罩5000盒,第三天生产口罩7200盒,若每天增长的百分率相同.
(1)求每天增长的百分率.
(2)经调查发现,1条生产线的最大产能是15000盒/天,但是每增加1条生产线,每条生产线的产能将减少500盒/天,现该厂要保证每天生产口罩65000盒,在增加产能的同时又要节省投入的条件下(生产线越多,投入越大),应该增加几条生产线?
参考答案
一、选择题(本大题共10小题,每小题4分,共40分)
1.已知点A(1,2021)在反比例函数的图象上,则k的值是( )
A.2021 B.﹣2021 C.1 D.﹣1
【分析】根据点A的坐标,利用反比例函数图象上点的坐标特征求出k值,此题得解.
解:∵点A(1,2021)在反比例函数的图象上,
∴k=1×2021=2021.
故选:A.
2.方程x2=5x的解是( )
A.x1=﹣5,x2=0 B.x1=5,x2=0 C.x=5 D.x=0
【分析】先把方程化为一般式,然后利用因式分解法解方程.
解:x2﹣5x=0,
x(x﹣5)=0,
x=0或x﹣5=0,
所以x1=0,x2=5.
故选:B.
3.已知=,则下列式子成立的是( )
A.3x=5y B.xy=15 C. D.
【分析】根据比例的性质逐个判断即可.
解:∵=,
∴两边都乘以5y,得5x=3y,
∵=,
∴两边都乘以3y,得xy=15,
∵=,
∴两边都乘以3x,得3y=5x,
即只有选项D符合题意;选项A、B、C都不符合题意;
故选:D.
4.对于反比例函数,下列说法不正确的是( )
A.图象分布在二、四象限内
B.图象经过点(1,﹣2021)
C.当x>0时,y随x的增大而增大
D.若点A(x1,y1),B(x2,y2)都在函数的图象上,且x1<x2时,则y1<y2
【分析】根据反比例函数图象的性质对各选项分析判断后利用排除法求解.
解:A、∵k=﹣2021<0,∴它的图象在第二、四象限,故本选项正确,不符合题意;
B、∵x=1时,y=﹣=﹣2021,∴点(1,﹣2021)在它的图象上,故本选项正确,不符合题意;
C、∵k=﹣2021<0,∴当x<0时,y随x的增大而增大,故本选项正确,不符合题意;
D、∵k=﹣2021<0,∴在每一个象限内,y随x的增大而增大,
∴当x1<x2<0,则y1<y2,故本选项错误,符合题意,
故选:D.
5.下列图形中一定是相似形的是( )
A.两个等边三角形 B.两个菱形
C.两个矩形 D.两个直角三角形
【分析】如果两个多边形的对应角相等,对应边的比相等,则这两个多边形是相似多边形.
解:∵等边三角形的对应角相等,对应边的比相等,
∴两个等边三角形一定是相似形,
又∵直角三角形,菱形的对应角不一定相等,矩形的边不一定对应成比例,
∴两个直角三角形、两个菱形、两个矩形都不一定是相似形,
故选:A.
6.若方程(x﹣2)2=k可以用直接开平方法解,则k的取值范围是( )
A.k≤0 B.k≥0 C.k<0 D.k≠0
【分析】若方程(x﹣2)2=k可以直接用开平方法解,则k≥0.
解:∵(x﹣2)2≥0,
∴k≥0.
故选:B.
7.已知点A(﹣1,a)与点B(2,b)都在反比例函数的图象上,则a与b之间的关系是( )
A.a>b B.a<b C.a≥b D.a=b
【分析】利用反比例函数的性质即可得出结论.
解:反比例函数中,k=12>0,
∴反比例函数的图象在一、三象限,
∵点A(﹣1,a)与点B(2,b)都在反比例函数的图象上,
∴A(﹣1,a)在第三象限,点B(2,b)在第一象限,
∴a<b,
故选:B.
8.关于x的一元二次方程(a﹣1)x2﹣2x+3=0有实数根,则整数a的最大值是( )
A.2 B.1 C.0 D.﹣1
【分析】根据方程有实数根,得到根的判别式的值大于等于0,且二次项系数不为0,即可求出整数a的最大值.
解:根据题意得:Δ=4﹣12(a﹣1)≥0,且a﹣1≠0,
解得:a≤,a≠1,
则整数a的最大值为0.
故选:C.
9.一个直角三角形的两直角边长分别为x,y,其面积为3,则y与x之间的关系用图象表示大致为( )
A. B.
C. D.
【分析】根据题意有:xy=6;故y与x之间的函数图象为反比例函数,且根据xy实际意义x、y应大于0,其图象在第一象限.
解:由题意得,
∴xy=6,
∴y=(x>0,y>0),
故选:C.
10.如图,在矩形ABCD中,E为DC边上一点,把△ADE沿AE翻折,使点D恰好落在BC边上的点F处,AB=4,AD=5,则EC的长为( )
A. B. C.2 D.3
【分析】先由矩形的性质得到AB=CD=4,AD=BC=5,再由折叠得到AF=AD=5,然后求得BF、CF的值,再设CE=x,则EF=ED=4﹣x,然后利用勾股定理列出方程求解,最后得到EC的长.
解:∵四边形ABCD是,
∴AB=CD=4,AD=BC=5,
由折叠得:AF=AD=5,EF=ED,
∴BF=3,
∴CF=BC﹣BF=5﹣3=2,
设CE=x,则EF=ED=4﹣x,
在Rt△EFC中,EC2+FC2=EF2,
∴x2+22=(4﹣x)2,
解得:x=,
∴EC=.
故选:A.
二、填空题(本大题共8个小题,每小题4分,请将答案填在答题卡的答案栏内).
11.若函数y=xn﹣1是关于x的反比例函数,则n的值为 0 .
【分析】根据反比例函数的定义得出n﹣1=﹣1,再求出n即可.
解:∵函数y=xn﹣1是关于x的反比例函数,
∴n﹣1=﹣1,
解得:n=0,
故答案为:0.
12.已知x=1是方程x2﹣ax+6=0的一个根,则a= 7 .
【分析】根据题意将x=1代入方程中即可求出答案.
解:由题意可知:x=1代入x2﹣ax+6=0
1﹣a+6=0
∴a=7
故答案为:7
13.已知AB∥CD,AD与BC相交于点O,若,AD=15,则DO的长为 9 .
【分析】由AB∥CD得出∠A=∠D,∠B=∠C,得出△AOB∽△DOC,进而得出,再根据,AD=15,即可得出OD的长.
解:∵AB∥CD,
∴∠A=∠D,∠B=∠C,
∴△AOB∽△DOC,
∴,
∵,AD=15,
∴,
∴OD=9,
故答案为:9.
14.当m >2 时,函数的图象在第一、三象限内.
【分析】根据反比例函数的性质得m﹣2>0,然后解不等式即可.
解:根据题意得m﹣2>0,
解得m>2.
故答案为:>2.
15.若方程(m﹣2)x|m|﹣x﹣2=0是一元二次方程,则m的值为 ﹣2 .
【分析】根据一元二次方程的定义得到m﹣2≠0且|m|=2,然后解方程和不等式即可得到满足条件的m的值.
解:∵关于x的方程(m﹣2)x|m|﹣x﹣2=0是一元二次方程,
∴|m|=2,m﹣2≠0,
解得m=﹣2;
故答案为:﹣2.
16.如图,若反比例函数与一次函数y2=ax+b交于A、B两点,当y1<y2时,则x的取值范围是 ﹣1<x<0或x>2 .
【分析】写出反比例函数的图象在一次函数的图象下方的自变量的取值范围即可.
解:观察图象可知,当y1<y2时,则x的取值范围是﹣1<x<0或x>2.
故答案为﹣1<x<0或x>2.
17.“杂交水稻之父”袁隆平为提高水稻的产量贡献了自己的一生,某试验田种植了杂交水稻,2019年平均亩产800千克,2021年平均亩产1000千克,设此水稻亩产量的平均增长率为x,则可列出的方程是 800(1+x)2=1000 .
【分析】设此水稻亩产量的平均增长率为x,根据“2019年平均亩产×(1+增长率)2=2021年平均亩产”即可列出关于x的方程,
解:设此水稻亩产量的平均增长率为x,则可列出的方程是800(1+x)2=1000.
故答案是:800(1+x)2=1000.
18.如图,在△ABC中,AB=4cm,BC=8cm,动点P从点A开始沿AB边运动,速度为1cm/s,动点Q从点B开始沿BC边运动,速度为2cm/s,如果P、Q两动点同时运动,那么经过 2或0.8 秒时,以B、Q、P为顶点的三角形与△ABC相似.
【分析】设经过t秒时,以△QBP与△ABC相似,则AP=t厘米,BP=(4﹣t)厘米,BQ=2t厘米,利用两组对应边的比相等且夹角对应相等的两个三角形相似进行分类讨论,由相似三角形的性质列出方程可求解.
解:设经过t秒时,以△QBP与△ABC相似,则AP=t厘米,BP=(4﹣t)厘米,BQ=2t厘米,
∵∠PBQ=∠ABC,
∴当时,△BPQ∽△BAC,即,解得t=2;
当时,△BPQ∽△BCA,即 ,解得t=0.8;
即经过2秒或0.8秒时,△QBP与△ABC相似.
故答案为2或0.8.
三、解答题(本大题共8个小题,共78分,解答题要求写出必要的文字说明或解答过程).
19.解方程:
(1)(x+1)2﹣9=0.
(2)x2﹣4x+1=0.
【分析】(1)利用直接开平方法求解即可;
(2)将常数项移到方程的右边,两边都加上一次项系数一半的平方配成完全平方式后,再开方即可得.
解:(1)(x+1)2﹣9=0,
(x+1)2=9,
∴x+1=3或x+1=﹣3,
∴x1=2,x2=﹣4;
(2)x2﹣4x+1=0,
x2﹣4x=﹣1,
x2﹣4x+4=3,即(x﹣2)2=3,
∴x﹣2=,
∴.
20.已知反比例函数(k≠0)的图象与一次函数y=ax+b的图象交于点A(﹣6,2),B(2,﹣6),且一次函数y=ax+b图象与x轴交于点C.
(1)求反比例函数与一次函数表达式;
(2)求△AOB的面积.
【分析】(1)根据待定系数法求解即可;
(2)求出C点的坐标,再根据三角形的面积公式求出三角形AOC和三角形BOC的面积,相加即可得出答案.
解:(1)把点A(﹣6,2)代入得,2=,
∴k=﹣12,
∴反比例函数的表达式为;
把点A(﹣6,2),B(2,﹣6)代入y=ax+b得,
解得:,
∴一次函数的表达式为y=﹣x﹣4;
(2)∵直线y=﹣x﹣4与x轴交于点C,
∴C(﹣4,0),
∴OC=4,
∴,
∴△AOB的面积为16.
21.如图,∠1=∠2,AB=3,AE=2,AC=12,AD=8.求证:∠C=∠D.
【分析】由∠1=∠2得出∠BAC=∠EAD,由AB=3,AE=2,AC=12,AD=8得出,进而得出△ABC∽△AED,即可得出∠C=∠D.
【解答】证明:∵∠1=∠2,
∴∠1+∠EAC=∠2+∠EAC,
即∠BAC=∠EAD,
∵AB=3,AE=2,AC=12,AD=8,
∴,,
∴,
∴△ABC∽△AED,
∴∠C=∠D.
22.对于实数m,n定义一种新运算“*”为:m*n=m2+mn,如3*2=32+3×2=15.
(1)若x*3=0,求x的值;
(2)如果关于x的方程x*2a=﹣5有两个相等的实数根,求a的值.
【分析】(1)先根据定义得出方程x2+3x=0,再解方程可求出x;
(2)先根据定义得出方程x2+2ax+5=0,再根据方程有两个相等的实数根即可求出a.
解:(1)∵x*3=0,
∴x2+3x=0,
∴x(x+3)=0,
x1=0,x2=﹣3,
∴x的值为0或﹣3;
(2)∵关于x的方程x*2a=﹣5有两个相等的实数根,
∴x2+2ax+5=0有两个相等的实数根,
∴(2a)2﹣4×1×5=0,
解得a1=,a2=﹣,
∴a的值为±.
23.已知a,b,c是△ABC的三边长,且.
(1)求的值;
(2)若△ABC的周长为60,求各边的长.
【分析】(1)直接设a=5k,b=4k,c=6k,进而代入求出答案;
(2)直接设a=5k,b=4k,c=6k,进而代入求出答案.
解:(1),
∴.
(2)∵△ABC的周长为60,
∴a+b+c=60,
∴5k+4k+6k=60,
∴k=4,
∴a=5k=20,b=4k=16,c=6k=24,
∴三角形的各边的长分别为20,16,24.
24.如图,已知在Rt△ABC中,∠ACB=90°,∠B=60°,点E,F分别是AC,AB边上的点,连结EF,且EF⊥AB.
(1)求证:△ABC∽△AEF;
(2)若AE=4,求△AEF的面积.
【分析】(1)由∠ACB=90°,EF⊥AB得出∠AFE=∠ACB=90°,由∠A是公共角,即可得出△ABC∽△AEF;
(2)利用含30°角的直角三角形的性质求出EF的长度,再由勾股定理得出AF的长度,即可求出△AEF的面积.
【解答】(1)证明:∵∠ACB=90°,EF⊥AB,
∴∠AFE=∠ACB=90°,
∵∠A=∠A,
∴△ABC∽△AEF,
(2)解:∵∠ACB=90°,∠B=60°
∴∠A=30°,
在△AEF中,∠AFE=90°,∠A=30°,AE=4
∴,
∴,
∴S△AEF=.
25.为了预防“流感”,某学校对教室采用药熏法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(毫克)与药物点燃后的时间x(分)成正比例,药物燃尽后,y与x成反比例(如图所示),已知药物点燃后6分钟燃尽,此时室内每立方米空气中含药量为12毫克.
(1)求药物燃烧时和药物燃尽后,y与x之间的函数表达式;
(2)研究表明:空气中每立方米的含药量不低于6毫克,且持续5分钟以上才能有效杀灭空气中的病菌,请计算说明此次消毒能否有效杀灭空气中的病菌.
【分析】(1)正比例函数图象过点(6,12),利用待定系数法可求解析式;反比例函数图象过点(6,12),利用待定系数法可求解析式;
(2)将y=6分别代入两个解析式,可求x的值,即可判断此次消毒能否有效杀灭空气中的病菌.
解:(1)设药物燃烧时,y与x之间函数的表达式为y=mx,
把(6,12)代入得,12=6m,
∴m=2,
∴药物燃烧时的函数表达式为y=2x(0≤x≤6);
设药物燃烧后,y与x之间函数的表达式为,
把(6,12)代入得,k=xy=6×12=72,
∴药物燃烧时的函数表达式为(x≥6);
(2)把y=6代入y=2x得,6=2x,
∴x=3,
把y=6代入得,,
∴x=12,
∵12﹣3=9>5,
∴此次消毒能有效杀灭空气中的病菌.
26.随着全球疫情的爆发,医疗物资需求猛增,某企业及时引进一条口罩生产线生产口罩,开工第一天生产口罩5000盒,第三天生产口罩7200盒,若每天增长的百分率相同.
(1)求每天增长的百分率.
(2)经调查发现,1条生产线的最大产能是15000盒/天,但是每增加1条生产线,每条生产线的产能将减少500盒/天,现该厂要保证每天生产口罩65000盒,在增加产能的同时又要节省投入的条件下(生产线越多,投入越大),应该增加几条生产线?
【分析】(1)设每天增长的百分率为x,利用第三天生产口罩的数量=第一天生产口罩的数量×(1+每天增长的百分率)2,即可得出关于x的一元二次方程,解之取其符合题意的值即可得出每天增长的百分率为20%;
(2)设增加y条生产线,则每条生产线的产量为(15000﹣500y)盒/天,利用生产线条数×每条生产线产能=总生产数,即可得出关于y的一元二次方程,解之即可得出y值,再结合要节省投入,即可得出应该增加4条生产线.
解:(1)设每天增长的百分率为x,
依题意得:5000(1+x)2=7200,
x1=0.2=20%,x2=﹣2.2(不合题意,舍去).
答:每天增长的百分率为20%.
(2)设增加y条生产线,则每条生产线的产量为(15000﹣500y)盒/天,
依题意得:(1+y)(15000﹣500y)=65000,
整理得:y2﹣29y+100=0,
解得:y1=4,y2=25.
又∵要节省投入,
∴y=4.
答:应该增加4条生产线.
同课章节目录
