2021-2022年高一上学期数学北师大版(2019)必修第一册第五章 函数应用 单元必刷卷(word含答案解析)
文档属性
| 名称 | 2021-2022年高一上学期数学北师大版(2019)必修第一册第五章 函数应用 单元必刷卷(word含答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 642.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-06 14:08:16 | ||
图片预览




文档简介
第五章 函数应用 单元必刷卷
一、单选题
1.若函数在区间内有零点,则( )
A.,(2)
B.(2)
C.在区间内,存在,使
D.以上说法都不正确
2.若函数y=f(x)在区间[a,b]上的图象是一条连续的曲线,则下列说法正确的是( )
A.若f(a)·f(b)>0,不存在实数c∈(a,b),使得f(c)=0
B.若f(a)·f(b)<0,存在且只存在一个实数c∈(a,b),使得f(c)=0
C.若f(a)·f(b)>0,有可能存在实数c∈(a,b),使得f(c)=0
D.若f(a)·f(b)<0,有可能不存在实数c∈(a,b),使得f(c)=0
3.某公司为激励创新,计划逐年加大研发资金投入.若该公司2014年全年投入研发资金130万元,在此基础上,每年投入的研发资金比上一年增长12%,则该公司全年投入的研发资金开始超过200万元的年份是(参考数据: )( )
A.2017年 B.2018年 C.2019年 D.2020年
4.当强度为x的声音对应的等级为分贝时,有(其中为常数).装修电钻的声音约为分贝,普通室内谈话的声音约为分贝.则装修电钻的声音强度与普通室内谈话的声音强度的比值为( )
A. B. C. D.
5.已知函数,若函数有13个零点,则实数的取值范围为( )
A. B.
C. D.
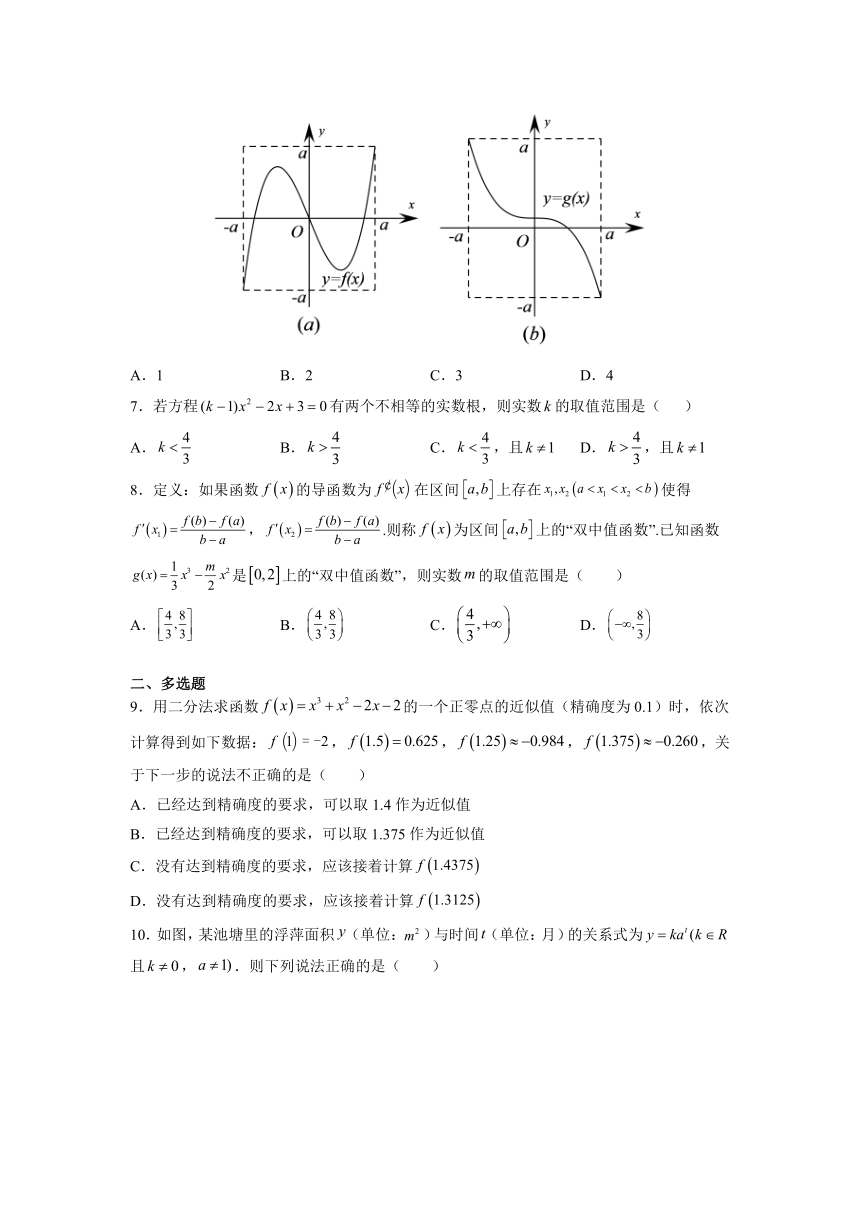
6.定义域和值域均为[﹣a,a](常数a>0)的函数y=f(x)和y=g(x)的图象如图所示,方程g[f(x)]=0解得个数不可能的是( )
A.1 B.2 C.3 D.4
7.若方程有两个不相等的实数根,则实数的取值范围是( )
A. B. C.,且 D.,且
8.定义:如果函数的导函数为在区间上存在使得,.则称为区间上的“双中值函数”.已知函数是上的“双中值函数”,则实数的取值范围是( )
A. B. C. D.
二、多选题
9.用二分法求函数的一个正零点的近似值(精确度为0.1)时,依次计算得到如下数据:,,,,关于下一步的说法不正确的是( )
A.已经达到精确度的要求,可以取1.4作为近似值
B.已经达到精确度的要求,可以取1.375作为近似值
C.没有达到精确度的要求,应该接着计算
D.没有达到精确度的要求,应该接着计算
10.如图,某池塘里的浮萍面积(单位:)与时间(单位:月)的关系式为且,.则下列说法正确的是( )
A.浮萍每月增加的面积都相等
B.第6个月时,浮萍的面积会超过
C.浮萍面积从蔓延到只需经过5个月
D.若浮萍面积蔓延到,,所经过的时间分别为,,,则
11.函数的一个正零点所在的区间不可能是( )
A. B. C. D.
12.已知函数,且实数,满足,若实数是函数的一个零点,那么下列不等式中可能成立的是( )
A. B. C. D.
三、填空题
13.函数的两个零点分别在区间和之内,则实数的取值范围为_________.
14.设函数,若且,则的取值范围是________.
15.某汽车在同一时间内速度 (单位:)与耗油量(单位:)之间有近似的函数关系,则车速为_____时,汽车的耗油量最少.
16.《算法统宗》中有如下问题:“哑子来买肉,难言钱数目,一斤少三十,八两多十八,试问能算者,合与多少肉”,意思是一个哑子来买肉,说不出钱的数目,买一斤(两)还差文钱,买八两多十八文钱,求肉数和肉价,则该问题中,肉价是每两__________文.
四、解答题
17.通过研究学生的学习行为,心理学家发现,学生接受能力依赖于老师引入概念和描述问题所用的时间,讲座开始时,学生的兴趣激增,中间有一段不太长的时间,学生的兴趣保持理想的状态,随后学生的注意力开始分散.分析结果和实验表明,用表示学生掌握和接收概念的能力(的值越大,表示接受能力越强),表示提出和讲授概念的时间(单位:分钟),可以有以下公式:
(1)开讲多少分钟后,学生的接受能力最强?能维持多长时间?
(2)开讲5分钟与开讲20分钟比较,学生的接受能力何时强一些?
18.已知函数,
(1)画出函数的图像,并写出其值域.
(2)当为何值时,函数在上有两个零点?
19.某企业开发一种新产品,现准备投入适当的广告费对产品进行促销,在一年内,预计年销量(万件)与广告费(万元)之间的函数关系为,已知生产此产品的年固定投入为万元,每生产万件此产品仍需要投入万元,若年销售额为“年生产成本的”与“年广告费的”之和,而当年产销量相等:
(1)试将年利润(万元)表示为年广告费(万元)的函数;
(2)求当年广告费投入多少万元时,企业利润最大
20.设关于的方程.
(1)若常数,求此方程的解;
(2)若该方程在内有解,求的取值范围.
21.保护环境,防治环境污染越来越得到人们的重视,某企业在现有设备下每日生产总成本(单位:万元)与日产量(单位:吨)之间的函数关系式为.现为了减少大气污染,该企业引进了除尘设备,每吨产品除尘费用为万元,除尘后,当日产量时,每日生产总成本.
(1)求的值;
(2)若每吨产品出厂价为48万元,试求除尘后日产量为多少吨时,每吨产品的利润最大,最大利润为多少万元?
22.已知函数f(x)=ax2+2x﹣2﹣a(a≤0),
(1)若a=﹣1,求函数的零点;
(2)若函数在区间(0,1]上恰有一个零点,求a的取值范围.
参考答案
1.D
【分析】
根据零点存在定理的内容,结合特例,即可选择判断.
【解析】若函数,
显然故、、都是错误的,正确的为.
故选:D.
【点睛】
本题考查零点存在定理的理解,注意函数连续性的要求,属简单题.
2.C
【分析】
根据零点存在性定理,直接判断命题是否正确.
【解析】根据函数零点存在定理进行判断,若f(a)·f(b)<0,则一定存在实数c∈(a,b),使得f(c)=0,但c的个数不确定,故B,D错误.若f(a)·f(b)>0,有可能存在实数c∈(a,b),使得f(c)=0,如,f(-2)f(2)>0,但在区间(-2,2)内有两个零点,故A错误,C正确.
故选:C
【点睛】
本题考查零点存在性定理的命题判断,属于基础题型,本题的关键是理解零点存在性定理.
3.D
【分析】
先设经过年后全年投入的研发资金开始超过200万元,根据题意,得到,求解,即可得出结果.
【解析】设经过年后全年投入的研发资金开始超过200万元,
由题意可得,则,
即,
因为,
所以,故.
故选:D.
【点睛】
本题主要考查指数函数模型的应用,涉及对数的运算,属于基础题型.
4.C
【分析】
设装修电钻的声音强度为,普通室内谈话的声音强度为,由装修电钻的声音约为分贝,普通室内谈话的声音约为分贝,列出方程组解出,,可得出的值,得到答案.
【解析】设装修电钻的声音强度为,普通室内谈话的声音强度为,
由题意,,
所以装修电钻的声音强度和普通室内谈话的声音强度比值为
.
故选:C
【点睛】
本题考查函数的实际应用问题,考查对数的性质、运算法则等基础知识,属于基础题.
5.D
【分析】
先根据题意将问题转化为数与函数的图象交点个数问题,再画出图形,数形结合即可解决.
【解析】解:函数有13个零点,
令,有,
设,
可知恒过定点,
画出函数,的图象,如图所示:
则函数与函数的图象有13个交点,
由图象可得:,则,
即,解得:.
故选:D.
【点睛】
本题考查根据函数零点个数求解参数范围问题,考查化归转化思想与数形结合思想,是中档题.
6.D
【分析】
由图象知有一个上的正根,结合图象可知根的个数.
【解析】因为时,有唯一解,
不妨设唯一解为,由图象可知,
则由g[f(x)]=0可得,
因为,由图象可知,可能有1根,2根,3个根,不可能又4个根,
故选:D
【点睛】
本题考查根的存在性及根的个数判断,函数的图象,考查逻辑思维能力,数形结合思想,属于中档题.
7.C
【分析】
由题意可得,从而可求出实数的取值范围.
【解析】解:由方程有两个不相等的实数根可知,此方程为一元二次方程且判别式大于零,即可得
,解得,且.
故选:C.
【点睛】
本题考查了一元二次方程根的分布问题.本题的关键是由不同两根得判别式大于零.本题的易错点是忽略了这一条件.
8.B
【分析】
求出导函数,根据“双中值函数”的定义可得方程在区间上有两解,利用一元二次方程根的分布列不等式组求解即可.
【解析】函数,
.函数是区间上的双中值函数,
在区间上存在,
满足,
,,
即方程在区间上有两解.
令,
,
解得.故实数的取值范围是.
故选:B.
【点睛】
本题主要考查导数的应用,考查了新定义问题,属于难题. 新定义题型的特点是:通过给出一个新概念,或约定一种新运算,或给出几个新模型来创设全新的问题情景,要求考生在阅读理解的基础上,依据题目提供的信息,联系所学的知识和方法,实现信息的迁移,达到灵活解题的目的.遇到新定义问题,应耐心读题,分析新定义的特点,弄清新定义的性质,按新定义的要求,“照章办事”,逐条分析、验证、运算,使问题得以解决.
9.ABD
【分析】
利用二分法判断出方程根的分布区间,即可根据精确度求出根的近似值.
【解析】解:由二分法知,方程的根在区间内,
没有达到精确度的要求,应该接着计算,
故选:ABD.
10.BCD
【分析】
由题意结合函数图象可得,进而可得;由函数图象的类型可判断A;代入可判断B;代入、可判断C;代入、、,结合对数的运算法则即可得判断D;即可得解.
【解析】由题意可知,函数过点和点,则,
解得(负值舍去),
函数关系式为,
对于A,由函数是曲线型函数,所以浮萍每月增加的面积不相等,故选项A错误;
对于B,当时,,故选项B正确;
对于C,令得;令得,所以浮萍面积从增加到需要5个月,故选项C正确;
对于D,令得;令得;令得;
所以,故选项D正确.
故选:BCD.
【点睛】
本题考查了函数解析式的确定及函数模型的应用,考查了运算求解能力,合理转化条件是解题关键,属于基础题.
11.ABC
【分析】
判断函数的单调性,利用零点的存在性定理得到零点所在的区间,由此即可判断的正零点不可能在的区间.
【解析】因为在上是增函数,所以至多有一个零点,
又因为,所以有且仅有一个零点且零点在内,
所以的正零点不可能在内.
故选:ABC.
【点睛】
本题考查函数的零点存在性定理的应用,难度较易.判断零点个数时,注意单调函数的零点至多有 个.
12.ABC
【分析】
由题意,确定函数为增函数,进而得知,,中一项为负的,两项为正的,或者三项都是负的,分类讨论分别求得可能成立选项,从而得到答案.
【解析】由函数的单调性可得,函数在为增函数,
由, 则为负数的个数为奇数,
对于选项,选项可能成立
对于选项,当时,函数的单调性可得:
即不满足,故选项不可能成立,故选:
【点睛】
本题考查了函数的单调性,属于中档题.
13.
【分析】
将函数零点问题转化为方程在区间和之内有根的问题,根据二次方程根的分布,列不等式求解即可.
【解析】解:令,得,
整理得,
因为函数的两个零点分别在区间和之内,即方程的根在区间和之内,
则,解得,
故答案为:.
【点睛】
本题考查函数零点分布问题,转化为方程的根的分布问题,考查学生转化的思想以及计算能力,是基础题.
14.
【分析】
可先画出函数图像,结合图像,对化简,根据的范围求解即可
【解析】如图所示:
的两根为,,则
又由可得,(对称性)
故,由图可知
所以
故答案为
【点睛】
本题考查分段函数图像的画法,根据函数图像的交点求解取值范围问题,综合性强,数形结合大大减小了试题难度,根与函数图像关系值得深入研究,是一道好题
15.35
【分析】
利用二次函数的性质可求耗油量最少时对应的的值.
【解析】因为可化简
,故当时,汽车的耗油量最少.
故填.
【点睛】
本题考查二次函数在实际问题中的应用,属于基础题.
16.6
【分析】
设肉价是每两文,根据题意列出方程可解得答案.
【解析】设肉价是每两文,由题意得,解得,即肉价是每两文.
【点睛】
本题考查中国古代著作中的数学问题,属数学文化,正确地理解题意是解题关键.
17.(1)开讲10钟后,学生的接受能力最强,能维持6分钟;(2)开讲5分钟时学生的接受能力比开讲20分钟时要强一些.
【分析】
(1)求出分段函数各段的函数值的范围,即可得结论;
(2)通过计算与的大小,即可得结论.
【解析】(1)依题意,当时,
,
故在单调递增,最大值为;
当时,;
当时,是减函数,
且.
因此开讲10钟后,学生的接受能力最强,能维持6分钟.
(2),
.
所以开讲5分钟时学生的接受能力比开讲20分钟时要强一些.
【点睛】
本题考查函数模型的性质与应用,考查分析问题、解决问题的能力,注意解题方法的积累,属于中档题.
18.(1)图象见解析;值域为.(2)
【分析】
(1)将函数解析式整理得到,根据题中条件,结合二次函数图像的画法,即可作出函数图像,由图像可得出值域;
(2)将函数在上有两个零点,转化为函数与的图像有两个交点,由(1)中图像,即可求出结果.
【解析】(1)依题意得,,其图像如图所示.
由图可知,函数的值域为.
(2)∵函数在上有两个零点,
∴方程在上有两个相异的实数根,
即函数与的图像有两个交点.
由(1)所作图像可知,,
∴.
∴当时,函数与的图像有两个交点,
即函数在上有两个零点.
【点睛】
本题主要考查二次函数的图像,以及由函数零点求参数的问题,熟记二次函数的图像与性质,灵活运用数形结合的思想,以及转化与化归的思想,即可求解,属于常考题型.
19.(1);(2)当年广告费投入8万元时,企业年利润最大
【分析】
(1)用年销售额减去广告费用和投入成本得出利润;
(2)利用基本不等式求出利润最大值及其对应的的值.
【解析】解:(1)
,
即
(2),
当且仅当时,即时取等号,
答:当年广告费投入8万元时,企业年利润最大,最大值为万元.
【点睛】
本题考查了基本不等式在求函数最值中的应用,属于中档题.
20.(1);(2).
【分析】
(1)将代入方程,得到,将其整理得到,集合指数函数的值域,得到,从而得到,求得结果;
(2)将式子整理得出,令,则,借助于二次函数在某个区间上的值域求得最后的结果.
【解析】(1)当时,方程即为,
化简得,即,
解得(舍去)或,
所以,所以,此方程的解为,
(2)由可得,
所以,
令,则,
所以,
由可得当时,最小值为,
当时,的最大值为,
所以,即,
所以的取值范围是.
【点睛】
该题考查的是有关求方程的解或者方程在某个区间上有解求参数的取值范围的问题,在解题的过程中,注意换元思想的应用,以及二次函数在某个区间上的值域的求解方法,属于中档题目.
21.(1)k=2; (2)日产量为4吨时,每吨产品的利润最大,最大利润为26万元.
【分析】
(1)求出除尘后的函数解析式,利用当日产量时,总成本,代入计算得;
(2)求出每吨产品的利润,利用基本不等式求解即可.
【解析】解:(1)由题意,除尘后,
将,代入得解得;
(2)由(1)值,总利润,
则每吨产品的利润,
当且仅当,即时取等号,
所以除尘后日产量为吨时,每吨产品的利润最大,最大利润为万元.
【点睛】
本题考查将实际问题的最值问题转化为函数的最值问题,考查学生的计算能力,属于中档题
22.(1)当a=﹣1时,函数f(x)的零点是1;(2)﹣1≤a≤0或a≤﹣2.
【分析】
(1)令f(x)=﹣x2+2x﹣1=0,求解即可;
(2)讨论当a=0时和当a<0时二次函数在区间(0,1]的零点分别求参数范围即可.
【解析】(1)当a=﹣1时,f(x)=﹣x2+2x﹣1,
令f(x)=﹣x2+2x﹣1=0,
解得x=1,
∴当a=﹣1时,函数f(x)的零点是1.
(2)①当a=0时,2x﹣2=0得x=1,符合题意.
②当a<0时,f(x)=ax2+2x﹣2﹣a=a(x﹣1)(x+),
则x1=1,x2=﹣,
由于函数在区间(0,1]上恰有一个零点,则﹣ 或﹣≤0,
解得 或a≤﹣2,
综上可得,a的取值范围为﹣1≤a≤0或a≤﹣2.
一、单选题
1.若函数在区间内有零点,则( )
A.,(2)
B.(2)
C.在区间内,存在,使
D.以上说法都不正确
2.若函数y=f(x)在区间[a,b]上的图象是一条连续的曲线,则下列说法正确的是( )
A.若f(a)·f(b)>0,不存在实数c∈(a,b),使得f(c)=0
B.若f(a)·f(b)<0,存在且只存在一个实数c∈(a,b),使得f(c)=0
C.若f(a)·f(b)>0,有可能存在实数c∈(a,b),使得f(c)=0
D.若f(a)·f(b)<0,有可能不存在实数c∈(a,b),使得f(c)=0
3.某公司为激励创新,计划逐年加大研发资金投入.若该公司2014年全年投入研发资金130万元,在此基础上,每年投入的研发资金比上一年增长12%,则该公司全年投入的研发资金开始超过200万元的年份是(参考数据: )( )
A.2017年 B.2018年 C.2019年 D.2020年
4.当强度为x的声音对应的等级为分贝时,有(其中为常数).装修电钻的声音约为分贝,普通室内谈话的声音约为分贝.则装修电钻的声音强度与普通室内谈话的声音强度的比值为( )
A. B. C. D.
5.已知函数,若函数有13个零点,则实数的取值范围为( )
A. B.
C. D.
6.定义域和值域均为[﹣a,a](常数a>0)的函数y=f(x)和y=g(x)的图象如图所示,方程g[f(x)]=0解得个数不可能的是( )
A.1 B.2 C.3 D.4
7.若方程有两个不相等的实数根,则实数的取值范围是( )
A. B. C.,且 D.,且
8.定义:如果函数的导函数为在区间上存在使得,.则称为区间上的“双中值函数”.已知函数是上的“双中值函数”,则实数的取值范围是( )
A. B. C. D.
二、多选题
9.用二分法求函数的一个正零点的近似值(精确度为0.1)时,依次计算得到如下数据:,,,,关于下一步的说法不正确的是( )
A.已经达到精确度的要求,可以取1.4作为近似值
B.已经达到精确度的要求,可以取1.375作为近似值
C.没有达到精确度的要求,应该接着计算
D.没有达到精确度的要求,应该接着计算
10.如图,某池塘里的浮萍面积(单位:)与时间(单位:月)的关系式为且,.则下列说法正确的是( )
A.浮萍每月增加的面积都相等
B.第6个月时,浮萍的面积会超过
C.浮萍面积从蔓延到只需经过5个月
D.若浮萍面积蔓延到,,所经过的时间分别为,,,则
11.函数的一个正零点所在的区间不可能是( )
A. B. C. D.
12.已知函数,且实数,满足,若实数是函数的一个零点,那么下列不等式中可能成立的是( )
A. B. C. D.
三、填空题
13.函数的两个零点分别在区间和之内,则实数的取值范围为_________.
14.设函数,若且,则的取值范围是________.
15.某汽车在同一时间内速度 (单位:)与耗油量(单位:)之间有近似的函数关系,则车速为_____时,汽车的耗油量最少.
16.《算法统宗》中有如下问题:“哑子来买肉,难言钱数目,一斤少三十,八两多十八,试问能算者,合与多少肉”,意思是一个哑子来买肉,说不出钱的数目,买一斤(两)还差文钱,买八两多十八文钱,求肉数和肉价,则该问题中,肉价是每两__________文.
四、解答题
17.通过研究学生的学习行为,心理学家发现,学生接受能力依赖于老师引入概念和描述问题所用的时间,讲座开始时,学生的兴趣激增,中间有一段不太长的时间,学生的兴趣保持理想的状态,随后学生的注意力开始分散.分析结果和实验表明,用表示学生掌握和接收概念的能力(的值越大,表示接受能力越强),表示提出和讲授概念的时间(单位:分钟),可以有以下公式:
(1)开讲多少分钟后,学生的接受能力最强?能维持多长时间?
(2)开讲5分钟与开讲20分钟比较,学生的接受能力何时强一些?
18.已知函数,
(1)画出函数的图像,并写出其值域.
(2)当为何值时,函数在上有两个零点?
19.某企业开发一种新产品,现准备投入适当的广告费对产品进行促销,在一年内,预计年销量(万件)与广告费(万元)之间的函数关系为,已知生产此产品的年固定投入为万元,每生产万件此产品仍需要投入万元,若年销售额为“年生产成本的”与“年广告费的”之和,而当年产销量相等:
(1)试将年利润(万元)表示为年广告费(万元)的函数;
(2)求当年广告费投入多少万元时,企业利润最大
20.设关于的方程.
(1)若常数,求此方程的解;
(2)若该方程在内有解,求的取值范围.
21.保护环境,防治环境污染越来越得到人们的重视,某企业在现有设备下每日生产总成本(单位:万元)与日产量(单位:吨)之间的函数关系式为.现为了减少大气污染,该企业引进了除尘设备,每吨产品除尘费用为万元,除尘后,当日产量时,每日生产总成本.
(1)求的值;
(2)若每吨产品出厂价为48万元,试求除尘后日产量为多少吨时,每吨产品的利润最大,最大利润为多少万元?
22.已知函数f(x)=ax2+2x﹣2﹣a(a≤0),
(1)若a=﹣1,求函数的零点;
(2)若函数在区间(0,1]上恰有一个零点,求a的取值范围.
参考答案
1.D
【分析】
根据零点存在定理的内容,结合特例,即可选择判断.
【解析】若函数,
显然故、、都是错误的,正确的为.
故选:D.
【点睛】
本题考查零点存在定理的理解,注意函数连续性的要求,属简单题.
2.C
【分析】
根据零点存在性定理,直接判断命题是否正确.
【解析】根据函数零点存在定理进行判断,若f(a)·f(b)<0,则一定存在实数c∈(a,b),使得f(c)=0,但c的个数不确定,故B,D错误.若f(a)·f(b)>0,有可能存在实数c∈(a,b),使得f(c)=0,如,f(-2)f(2)>0,但在区间(-2,2)内有两个零点,故A错误,C正确.
故选:C
【点睛】
本题考查零点存在性定理的命题判断,属于基础题型,本题的关键是理解零点存在性定理.
3.D
【分析】
先设经过年后全年投入的研发资金开始超过200万元,根据题意,得到,求解,即可得出结果.
【解析】设经过年后全年投入的研发资金开始超过200万元,
由题意可得,则,
即,
因为,
所以,故.
故选:D.
【点睛】
本题主要考查指数函数模型的应用,涉及对数的运算,属于基础题型.
4.C
【分析】
设装修电钻的声音强度为,普通室内谈话的声音强度为,由装修电钻的声音约为分贝,普通室内谈话的声音约为分贝,列出方程组解出,,可得出的值,得到答案.
【解析】设装修电钻的声音强度为,普通室内谈话的声音强度为,
由题意,,
所以装修电钻的声音强度和普通室内谈话的声音强度比值为
.
故选:C
【点睛】
本题考查函数的实际应用问题,考查对数的性质、运算法则等基础知识,属于基础题.
5.D
【分析】
先根据题意将问题转化为数与函数的图象交点个数问题,再画出图形,数形结合即可解决.
【解析】解:函数有13个零点,
令,有,
设,
可知恒过定点,
画出函数,的图象,如图所示:
则函数与函数的图象有13个交点,
由图象可得:,则,
即,解得:.
故选:D.
【点睛】
本题考查根据函数零点个数求解参数范围问题,考查化归转化思想与数形结合思想,是中档题.
6.D
【分析】
由图象知有一个上的正根,结合图象可知根的个数.
【解析】因为时,有唯一解,
不妨设唯一解为,由图象可知,
则由g[f(x)]=0可得,
因为,由图象可知,可能有1根,2根,3个根,不可能又4个根,
故选:D
【点睛】
本题考查根的存在性及根的个数判断,函数的图象,考查逻辑思维能力,数形结合思想,属于中档题.
7.C
【分析】
由题意可得,从而可求出实数的取值范围.
【解析】解:由方程有两个不相等的实数根可知,此方程为一元二次方程且判别式大于零,即可得
,解得,且.
故选:C.
【点睛】
本题考查了一元二次方程根的分布问题.本题的关键是由不同两根得判别式大于零.本题的易错点是忽略了这一条件.
8.B
【分析】
求出导函数,根据“双中值函数”的定义可得方程在区间上有两解,利用一元二次方程根的分布列不等式组求解即可.
【解析】函数,
.函数是区间上的双中值函数,
在区间上存在,
满足,
,,
即方程在区间上有两解.
令,
,
解得.故实数的取值范围是.
故选:B.
【点睛】
本题主要考查导数的应用,考查了新定义问题,属于难题. 新定义题型的特点是:通过给出一个新概念,或约定一种新运算,或给出几个新模型来创设全新的问题情景,要求考生在阅读理解的基础上,依据题目提供的信息,联系所学的知识和方法,实现信息的迁移,达到灵活解题的目的.遇到新定义问题,应耐心读题,分析新定义的特点,弄清新定义的性质,按新定义的要求,“照章办事”,逐条分析、验证、运算,使问题得以解决.
9.ABD
【分析】
利用二分法判断出方程根的分布区间,即可根据精确度求出根的近似值.
【解析】解:由二分法知,方程的根在区间内,
没有达到精确度的要求,应该接着计算,
故选:ABD.
10.BCD
【分析】
由题意结合函数图象可得,进而可得;由函数图象的类型可判断A;代入可判断B;代入、可判断C;代入、、,结合对数的运算法则即可得判断D;即可得解.
【解析】由题意可知,函数过点和点,则,
解得(负值舍去),
函数关系式为,
对于A,由函数是曲线型函数,所以浮萍每月增加的面积不相等,故选项A错误;
对于B,当时,,故选项B正确;
对于C,令得;令得,所以浮萍面积从增加到需要5个月,故选项C正确;
对于D,令得;令得;令得;
所以,故选项D正确.
故选:BCD.
【点睛】
本题考查了函数解析式的确定及函数模型的应用,考查了运算求解能力,合理转化条件是解题关键,属于基础题.
11.ABC
【分析】
判断函数的单调性,利用零点的存在性定理得到零点所在的区间,由此即可判断的正零点不可能在的区间.
【解析】因为在上是增函数,所以至多有一个零点,
又因为,所以有且仅有一个零点且零点在内,
所以的正零点不可能在内.
故选:ABC.
【点睛】
本题考查函数的零点存在性定理的应用,难度较易.判断零点个数时,注意单调函数的零点至多有 个.
12.ABC
【分析】
由题意,确定函数为增函数,进而得知,,中一项为负的,两项为正的,或者三项都是负的,分类讨论分别求得可能成立选项,从而得到答案.
【解析】由函数的单调性可得,函数在为增函数,
由, 则为负数的个数为奇数,
对于选项,选项可能成立
对于选项,当时,函数的单调性可得:
即不满足,故选项不可能成立,故选:
【点睛】
本题考查了函数的单调性,属于中档题.
13.
【分析】
将函数零点问题转化为方程在区间和之内有根的问题,根据二次方程根的分布,列不等式求解即可.
【解析】解:令,得,
整理得,
因为函数的两个零点分别在区间和之内,即方程的根在区间和之内,
则,解得,
故答案为:.
【点睛】
本题考查函数零点分布问题,转化为方程的根的分布问题,考查学生转化的思想以及计算能力,是基础题.
14.
【分析】
可先画出函数图像,结合图像,对化简,根据的范围求解即可
【解析】如图所示:
的两根为,,则
又由可得,(对称性)
故,由图可知
所以
故答案为
【点睛】
本题考查分段函数图像的画法,根据函数图像的交点求解取值范围问题,综合性强,数形结合大大减小了试题难度,根与函数图像关系值得深入研究,是一道好题
15.35
【分析】
利用二次函数的性质可求耗油量最少时对应的的值.
【解析】因为可化简
,故当时,汽车的耗油量最少.
故填.
【点睛】
本题考查二次函数在实际问题中的应用,属于基础题.
16.6
【分析】
设肉价是每两文,根据题意列出方程可解得答案.
【解析】设肉价是每两文,由题意得,解得,即肉价是每两文.
【点睛】
本题考查中国古代著作中的数学问题,属数学文化,正确地理解题意是解题关键.
17.(1)开讲10钟后,学生的接受能力最强,能维持6分钟;(2)开讲5分钟时学生的接受能力比开讲20分钟时要强一些.
【分析】
(1)求出分段函数各段的函数值的范围,即可得结论;
(2)通过计算与的大小,即可得结论.
【解析】(1)依题意,当时,
,
故在单调递增,最大值为;
当时,;
当时,是减函数,
且.
因此开讲10钟后,学生的接受能力最强,能维持6分钟.
(2),
.
所以开讲5分钟时学生的接受能力比开讲20分钟时要强一些.
【点睛】
本题考查函数模型的性质与应用,考查分析问题、解决问题的能力,注意解题方法的积累,属于中档题.
18.(1)图象见解析;值域为.(2)
【分析】
(1)将函数解析式整理得到,根据题中条件,结合二次函数图像的画法,即可作出函数图像,由图像可得出值域;
(2)将函数在上有两个零点,转化为函数与的图像有两个交点,由(1)中图像,即可求出结果.
【解析】(1)依题意得,,其图像如图所示.
由图可知,函数的值域为.
(2)∵函数在上有两个零点,
∴方程在上有两个相异的实数根,
即函数与的图像有两个交点.
由(1)所作图像可知,,
∴.
∴当时,函数与的图像有两个交点,
即函数在上有两个零点.
【点睛】
本题主要考查二次函数的图像,以及由函数零点求参数的问题,熟记二次函数的图像与性质,灵活运用数形结合的思想,以及转化与化归的思想,即可求解,属于常考题型.
19.(1);(2)当年广告费投入8万元时,企业年利润最大
【分析】
(1)用年销售额减去广告费用和投入成本得出利润;
(2)利用基本不等式求出利润最大值及其对应的的值.
【解析】解:(1)
,
即
(2),
当且仅当时,即时取等号,
答:当年广告费投入8万元时,企业年利润最大,最大值为万元.
【点睛】
本题考查了基本不等式在求函数最值中的应用,属于中档题.
20.(1);(2).
【分析】
(1)将代入方程,得到,将其整理得到,集合指数函数的值域,得到,从而得到,求得结果;
(2)将式子整理得出,令,则,借助于二次函数在某个区间上的值域求得最后的结果.
【解析】(1)当时,方程即为,
化简得,即,
解得(舍去)或,
所以,所以,此方程的解为,
(2)由可得,
所以,
令,则,
所以,
由可得当时,最小值为,
当时,的最大值为,
所以,即,
所以的取值范围是.
【点睛】
该题考查的是有关求方程的解或者方程在某个区间上有解求参数的取值范围的问题,在解题的过程中,注意换元思想的应用,以及二次函数在某个区间上的值域的求解方法,属于中档题目.
21.(1)k=2; (2)日产量为4吨时,每吨产品的利润最大,最大利润为26万元.
【分析】
(1)求出除尘后的函数解析式,利用当日产量时,总成本,代入计算得;
(2)求出每吨产品的利润,利用基本不等式求解即可.
【解析】解:(1)由题意,除尘后,
将,代入得解得;
(2)由(1)值,总利润,
则每吨产品的利润,
当且仅当,即时取等号,
所以除尘后日产量为吨时,每吨产品的利润最大,最大利润为万元.
【点睛】
本题考查将实际问题的最值问题转化为函数的最值问题,考查学生的计算能力,属于中档题
22.(1)当a=﹣1时,函数f(x)的零点是1;(2)﹣1≤a≤0或a≤﹣2.
【分析】
(1)令f(x)=﹣x2+2x﹣1=0,求解即可;
(2)讨论当a=0时和当a<0时二次函数在区间(0,1]的零点分别求参数范围即可.
【解析】(1)当a=﹣1时,f(x)=﹣x2+2x﹣1,
令f(x)=﹣x2+2x﹣1=0,
解得x=1,
∴当a=﹣1时,函数f(x)的零点是1.
(2)①当a=0时,2x﹣2=0得x=1,符合题意.
②当a<0时,f(x)=ax2+2x﹣2﹣a=a(x﹣1)(x+),
则x1=1,x2=﹣,
由于函数在区间(0,1]上恰有一个零点,则﹣ 或﹣≤0,
解得 或a≤﹣2,
综上可得,a的取值范围为﹣1≤a≤0或a≤﹣2.
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
