2.2 直线方程综合复习(知识梳理+例题+练习)(解析版)
文档属性
| 名称 | 2.2 直线方程综合复习(知识梳理+例题+练习)(解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-02 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
直线方程
知识点梳理
1.直线的倾斜角与斜率
(1)直线的倾斜角 ①定义:当直线与轴相交时,取轴作为基准,轴________与直线________方向之间所成的角叫做直线的倾斜角.当直线与轴平行或重合时,规定它的倾斜角为________.
②倾斜角的范围为______________.
(2)直线的斜率 ①定义:一条直线的倾斜角的________叫做这条直线的斜率,斜率常用小写字母表示,即________,倾斜角是的直线斜率不存在.
②过两点的直线的斜率公式:
注意:经过两点,的直线的斜率公式为______________________.当时,直线的斜率__________.
(3)直线的倾斜角与斜率的关系:,
当为锐角时,越大越____;当为钝角时,越大越____.
直线方程的五种基本形式
点斜式:,适于用经过定点的问题
斜截式:,适用于判定直线位置关系
两点式:
截距式:
一般式:,适用于点到直线的距离和判定直线的位置关系
3.两条直线平行与垂直的判定
(1)两条直线平行
对于两条不重合的直线、,其斜率分别为、,则有____________.特别地,当直线的斜率、都不存在时,与________.
(2)两条直线垂直
如果两条直线斜率、存在,设为、,则____________,当一条直线斜率为零,另一条直线斜率不存在时,两直线________.
4.三种距离公式
(1)点、间的距离:
.
(2)点到直线:的距离:
.
(3)两平行直线:与: ()间的距离为______________.
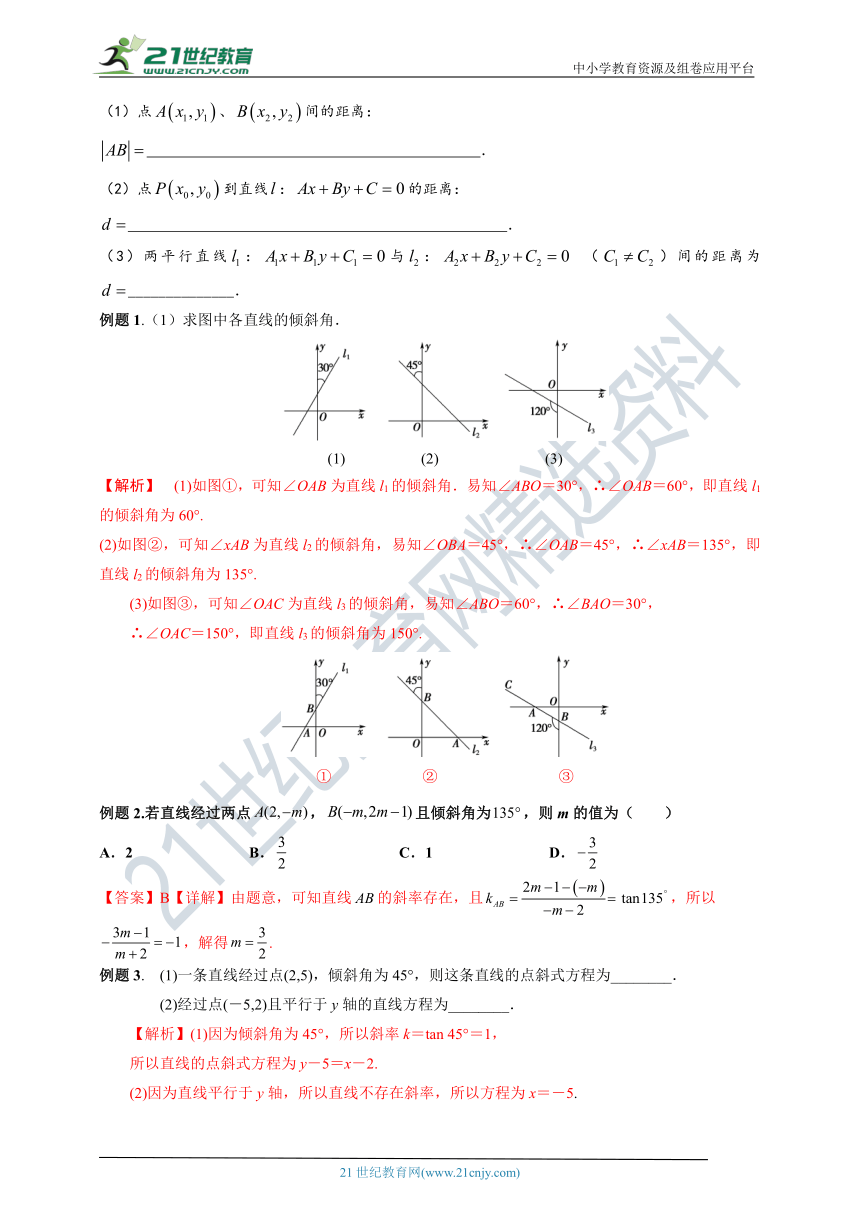
例题1.(1)求图中各直线的倾斜角.
(1) (2) (3)
【解析】 (1)如图①,可知∠OAB为直线l1的倾斜角.易知∠ABO=30°,∴∠OAB=60°,即直线l1的倾斜角为60°.
(2)如图②,可知∠xAB为直线l2的倾斜角,易知∠OBA=45°,∴∠OAB=45°,∴∠xAB=135°,即直线l2的倾斜角为135°.
(3)如图③,可知∠OAC为直线l3的倾斜角,易知∠ABO=60°,∴∠BAO=30°,
∴∠OAC=150°,即直线l3的倾斜角为150°.
① ② ③
例题2.若直线经过两点,且倾斜角为,则m的值为( )
A.2 B. C.1 D.
【答案】B【详解】由题意,可知直线的斜率存在,且,所以,解得.
例题3. (1)一条直线经过点(2,5),倾斜角为45°,则这条直线的点斜式方程为________.
(2)经过点(-5,2)且平行于y轴的直线方程为________.
【解析】(1)因为倾斜角为45°,所以斜率k=tan 45°=1,
所以直线的点斜式方程为y-5=x-2.
(2)因为直线平行于y轴,所以直线不存在斜率,所以方程为x=-5.
例题4:根据条件写出下列直线的斜截式方程:
(2)倾斜角为150°,在y轴上的截距是-2;
(3)倾斜角为60°,与y轴的交点到坐标原点的距离为3.
【解析】(1)因为倾斜角α=150°,所以斜率k=tan 150°=-,由斜截式可得直线方程为y=-x-2.
(3)因为直线的倾斜角为60°,所以斜率k=tan 60°=.因为直线与y轴的交点到坐标原点的距离为3,所以直线在y轴上的截距b=3或b=-3,故所求直线的斜截式方程为y=x+3或y=x-3.
例5..求过点(4,-3)且在两坐标轴上截距相等的直线l的方程.
【解析】 设直线在x轴、y轴上的截距分别为a,b.
①当a≠0,b≠0时,设l的方程为+=1.
∵点(4,-3)在直线上,∴+=1,
若a=b,则a=b=1,直线方程为x+y-1=0.
②当a=b=0时,直线过原点,且过点(4,-3),
∴直线的方程为3x+4y=0.
综上知,所求直线方程为x+y-1=0或3x+4y=0.
例6.(1)已知直线l1:2x+(m+1)y+4=0与直线l2:mx+3y-2=0平行,求m的值;
(2)当a为何值时,直线l1:(a+2)x+(1-a)y-1=0与直线l2:(a-1)x+(2a+3)y+2=0互相垂直.
【解析】 法一:(1)由l1:2x+(m+1)y+4=0,
l2:mx+3y-2=0知:①当m=0时,显然l1与l2不平行.
②当m≠0时,要使l1∥l2,需=≠.
解得m=2或m=-3,∴m的值为2或-3.
(2)由题意知,直线l1⊥l2.
①若1-a=0,即a=1时,直线l1:3x-1=0与直线l2:5y+2=0显然垂直.
②若2a+3=0,即a=-时,直线l1:x+5y-2=0与直线l2:5x-4=0不垂直.
③若1-a≠0且2a+3≠0,则直线l1,l2的斜率k1,k2都存在,k1=-,k2=-.
当l1⊥l2时,k1·k2=-1,
即·=-1,
∴a=-1.
综上可知,当a=1或a=-1时,直线l1⊥l2.
法二:(1)令2×3=m(m+1),
解得m=-3或m=2.
当m=-3时,l1:x-y+2=0,l2:3x-3y+2=0,
显然l1与l2不重合,∴l1∥l2.
同理当m=2时,l1:2x+3y+4=0,l2:2x+3y-2=0,
显然l1与l2不重合,∴l1∥l2,∴m的值为2或-3.
(2)由题意知直线l1⊥l2,
∴(a+2)(a-1)+(1-a)(2a+3)=0,解得a=±1,
将a=±1代入方程,均满足题意.
故当a=1或a=-1时,直线l1⊥l2.
例题7.不论为何值,直线恒过定点( )
A. B. C. D.
【答案】B【详解】
恒过定点,恒过定点,由解得即直线恒过定点.
例题8:已知△ABC的三个顶点坐标分别是A(1,-1),B(-1,3),C(3,0).
(1)判断△ABC的形状;
(2)求△ABC的面积.
【解析】(1)如图所示,△ABC为直角三角形,下面进行验证.
法一:∵|AB|==2,
|AC|==,|BC|==5.
∴|AB|2+|AC|2=|BC|2,即△ABC是以A为直角顶点的直角三角形.
法二:∵kAB==-2,kAC==.
∴kAB·kAC=-1,∴AB⊥AC.
∴△ABC是以A为直角顶点的直角三角形.
(2)由(1)中法一得|AB|=2,|AC|=.
又∵∠A=90°,∴S△ABC=|AB||AC|=×2×=5.
例题9.求点P(3,-2)到下列直线的距离:
①y=x+;②y=6;③x=4.
【解析】①把方程y=x+写成3x-4y+1=0,由点到直线的距离公式得d==.
②把方程y=6写成0·x+y-6=0,由点到直线的距离公式得d==8.
③因为直线x=4平行于y轴,
所以d=|4-3|=1.
例题10.已知直线l1过点A(0,1),l2过点B(5,0),如果l1∥l2,且l1与l2之间的距离为5,求l1,l2的方程.
【解析】当直线l1,l2斜率存在时,设直线l1、l2的斜率为k,由斜截式得l1的方程为y=kx+1,即kx-y+1=0,由点斜式得l2的方程为y=k(x-5),即kx-y-5k=0,在直线l1上取一点A(0,1),则点A到直线l2的距离d==5,∴25k2+10k+1=25k2+25,∴k=,
∴l1的方程为12x-5y+5=0,l2的方程为12x-5y-60=0.
若直线l1,l2的斜率不存在,则l1的方程为x=0,l2的方程为x=5,它们之间的距离为5,同样满足条件.
综上可知,满足条件的直线方程有两组,即l1:12x-5y+5=0,l2:12x-5y-60=0或l1:x=0,l2:x=5.
练习
1.直线,当变动时,所有直线恒过定点坐标为( )
A. B. C. D.
【答案】C【详解】把直线方程整理为,令,故,所以定点为,
2.已知点,在直线上,则的方程为( )
A. B.
C. D.
【答案】A【详解】根据截距式可得直线方程为:
即.
3.已知直线的方程为,则直线的倾斜角为( )
A. B. C. D.
【答案】D【详解】
因为直线的方程为,所以直线的斜率不存在,所以直线的倾斜角为,
4.若直线l过点且斜率,则l的方程为( )
A. B. C. D.
【答案】A【详解】
由点斜式可得直线方程为,整理得.故选:A.
5.已知斜率为的直线过直线与交点,则原点到直线的距离为( )
A. B. C. D.
【答案】A【详解】联立,,解得,
又直线斜率为,∴直线的方程为,即,
∴原点到直线的距离为.
6.已知两条直线,平行,则( )
A. B.或 C. D.或
【答案】D【详解】因为两条直线,平行,则,解得或.
7.直线的倾斜角为( )
A. B. C. D.
【答案】B【详解】将直线化为点斜式方程得,
所以直线的斜率为,
所以直线的倾斜角为.
8.直线的倾斜角为( )
A. B. C. D.
【答案】C【详解】
由可得直线的斜率为,设直线的倾斜角为,则,
因为,所以,
9.过点且斜率为的直线在轴上的截距是( )
A. B. C. D.
【答案】D【详解】所求直线方程为,该直线交轴于点,
因此,该直线在轴上的截距是.
10.在平面直角坐标系中,直线的倾斜角是( )
A. B. C. D.
【答案】C【详解】
直线即的倾斜角为,
11.斜率为,在x轴上截距为2的直线的一般式方程是( )
A. B. C. D.
【答案】C【详解】直线在轴上的截距为2,直线经过点(2,0),
又直线的斜率为,由直线的点斜式方程得直线的方程为,即,
故选:C.
12.直线l经过点,且与直线平行,则l的一般式方程为__________.
【答案】
【详解】因为直线经过点,且与直线平行,
所以可设直线l的方程为从而有,解得
13.已知直线l1:和l2:,且l1l2,则两直线l1和l2间的距离是_________.
【答案】【详解】
由题意知,,得,
解得,所以,
所以两直线间的距离为,
14.两条平行线之间的距离等于________.
【答案】2【详解】
由题意可得两平行线间的距离为
,
15.已知点A(-2,-2),B(a,2)且,则a的值为___________.
【答案】1或-5【详解】
∵点A(-2,-2),B(a,2),且或.
故答案为:1或-5.
16.直线必经过定点___________.
【答案】【详解】
由,得,
所以,解得,
即直线过定点.
17.设直线l过点A(-1,3),且和直线平行.
(1)求直线l的方程;
(2)设l与x轴相交于点B,求直线l绕点B逆时针旋转90°所得的直线方程.
【答案】(1)(2)
解:由题意得:直线l和直线平行
直线l的方程为:,解得:.
(2)l与x轴相交于点B(3,0)
直线l绕点B逆时针旋转90°所得的直线方程的斜率为:.
直线方程:,化简得:.
18.求满足下列条件的直线方程:
(1)过点,倾斜角为45°;(2)过两点.
【答案】
(1)
(2)
(1)所求直线方程为,即.
(2)所求直线方程为,即.
19.已知两点,.
(1)求直线AB的斜率k和倾斜角;
(2)求直线AB在y轴上的截距b.
【答案】
(1),
(2)
(1)根据题意,设直线AB的斜率为k,倾斜角为,
又由两点,,则,
则,因为所以,
(2)根据题意,直线AB的斜率,则其方程,
变形可得:,直线AB在y轴上的截距;
即.
20.已知的顶点.
(1)求边上的高所在直线的方程;
(2)求边上的中线所在直线的方程;
(3)的中位线与边平行,求所在直线的方程.
【答案】
(1)(2)(3)
(1)三角形的三个顶点是.
所以BC斜率为:,所以BC边上的高AD的斜率为:,BC边上的高AD所在直线的方程为:,即;
(2)顶点是则其中点,所以中线AP所在直线直线斜率,
所以中线AP所在直线方程为:,即.
(3)求出的中点,求出BC的斜率为:,由点斜式即可写出方程,即
21.的三个顶点是,,,求:
(1)边BC上的中线所在直线的方程;
(2)边BC的垂直平分线的方程.
【答案】(1)(2)
(1)解:BC的中点坐标为,
所以边BC上的中线的斜率为,
所以边BC上的中线所在直线的方程为.
(2)解:由(1)知BC的中点坐标,又,
所以边BC的垂直平分线的斜率为,
所以边BC的垂直平分线的方程为.
22.已知直线经过两点,问:当取何值时:
(1)与轴平行?(2)与轴平行?(3)的斜率为?
【答案】(1);(2);(3).
【详解】(1)当直线与轴平行时,直线的斜率为0,此时,得.
(2)当与轴平行时,直线不存在斜率,得.
(3)当的斜率为时,有,解得.
故当时,与轴平行;当时,与轴平行;当,的斜率为.
23.已知的三个顶点是
(1)求边的高所在直线方程;
(2)的面积
【答案】(1);(2)8.
【详解】(1)设边的高所在直线为,
由题知 则,
又点在直线上所以直线的方程为
即
(2)所在直线方程为: 即
点到的距离
又
则
24.已知直线;.
(1)若,求的值;
(2)若,且直线与直线之间的距离为,求、的值.
【答案】(1);(2)或.
【详解】(1)设直线的斜率分别为,则.
若,则,,
(2)若,则, ∴可以化简为,
又直线与直线的距离,或,综上:.
25.已知直线,求
(1)求直线l的斜率:
(2)若直线m与l平行,且过点,求直线m的方程.
【答案】(1);(2).
【详解】(1)由直线方程知:,即直线l的斜率为;
(2)由(1),根据直线m与l平行,且过点,则直线m:,
∴直线m一般形式为.
26.求原点到下列直线的距离:
(1) (2).
【答案】(1)(2)0
【详解】(1),(2)直线,则
27.求满足下列条件的直线方程.
(1)斜率为,经过点;(2)斜率为,在轴上的截距是;
(3)经过两点和;(4)经过两点和.
【答案】(1);(2);(3);(4).
【详解】(1)由题意可知直线的方程为,即为;
(2)由题意可知直线的方程为,即为;
(3)由题意可知直线的方程为,即为;
(4)由题意可知直线的方程为,即为.
28.三角形的三个顶点是,,.
(1)求边所在的直线方程;
(2)求边上的高所在的直线方程;
(3)求经过两边和中点的直线的方程.
【答案】(1);(2);(3).
【详解】(1)由,.可得边所在的直线方程是:,即.
(2)因为边上的高垂直于,(1)由已知
高所在的直线方程斜率为
又边上的高过点,
故所求直线方程为
故边上的高所在的直线方程是.
(3)经过两边和中点的直线平行于,
可设所求直线方程为.
由已知线段的中点为
.
解得:
故经过两边和中点的直线方程为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
直线方程
知识点梳理
1.直线的倾斜角与斜率
(1)直线的倾斜角 ①定义:当直线与轴相交时,取轴作为基准,轴________与直线________方向之间所成的角叫做直线的倾斜角.当直线与轴平行或重合时,规定它的倾斜角为________.
②倾斜角的范围为______________.
(2)直线的斜率 ①定义:一条直线的倾斜角的________叫做这条直线的斜率,斜率常用小写字母表示,即________,倾斜角是的直线斜率不存在.
②过两点的直线的斜率公式:
注意:经过两点,的直线的斜率公式为______________________.当时,直线的斜率__________.
(3)直线的倾斜角与斜率的关系:,
当为锐角时,越大越____;当为钝角时,越大越____.
直线方程的五种基本形式
点斜式:,适于用经过定点的问题
斜截式:,适用于判定直线位置关系
两点式:
截距式:
一般式:,适用于点到直线的距离和判定直线的位置关系
3.两条直线平行与垂直的判定
(1)两条直线平行
对于两条不重合的直线、,其斜率分别为、,则有____________.特别地,当直线的斜率、都不存在时,与________.
(2)两条直线垂直
如果两条直线斜率、存在,设为、,则____________,当一条直线斜率为零,另一条直线斜率不存在时,两直线________.
4.三种距离公式
(1)点、间的距离:
.
(2)点到直线:的距离:
.
(3)两平行直线:与: ()间的距离为______________.
例题1.(1)求图中各直线的倾斜角.
(1) (2) (3)
【解析】 (1)如图①,可知∠OAB为直线l1的倾斜角.易知∠ABO=30°,∴∠OAB=60°,即直线l1的倾斜角为60°.
(2)如图②,可知∠xAB为直线l2的倾斜角,易知∠OBA=45°,∴∠OAB=45°,∴∠xAB=135°,即直线l2的倾斜角为135°.
(3)如图③,可知∠OAC为直线l3的倾斜角,易知∠ABO=60°,∴∠BAO=30°,
∴∠OAC=150°,即直线l3的倾斜角为150°.
① ② ③
例题2.若直线经过两点,且倾斜角为,则m的值为( )
A.2 B. C.1 D.
【答案】B【详解】由题意,可知直线的斜率存在,且,所以,解得.
例题3. (1)一条直线经过点(2,5),倾斜角为45°,则这条直线的点斜式方程为________.
(2)经过点(-5,2)且平行于y轴的直线方程为________.
【解析】(1)因为倾斜角为45°,所以斜率k=tan 45°=1,
所以直线的点斜式方程为y-5=x-2.
(2)因为直线平行于y轴,所以直线不存在斜率,所以方程为x=-5.
例题4:根据条件写出下列直线的斜截式方程:
(2)倾斜角为150°,在y轴上的截距是-2;
(3)倾斜角为60°,与y轴的交点到坐标原点的距离为3.
【解析】(1)因为倾斜角α=150°,所以斜率k=tan 150°=-,由斜截式可得直线方程为y=-x-2.
(3)因为直线的倾斜角为60°,所以斜率k=tan 60°=.因为直线与y轴的交点到坐标原点的距离为3,所以直线在y轴上的截距b=3或b=-3,故所求直线的斜截式方程为y=x+3或y=x-3.
例5..求过点(4,-3)且在两坐标轴上截距相等的直线l的方程.
【解析】 设直线在x轴、y轴上的截距分别为a,b.
①当a≠0,b≠0时,设l的方程为+=1.
∵点(4,-3)在直线上,∴+=1,
若a=b,则a=b=1,直线方程为x+y-1=0.
②当a=b=0时,直线过原点,且过点(4,-3),
∴直线的方程为3x+4y=0.
综上知,所求直线方程为x+y-1=0或3x+4y=0.
例6.(1)已知直线l1:2x+(m+1)y+4=0与直线l2:mx+3y-2=0平行,求m的值;
(2)当a为何值时,直线l1:(a+2)x+(1-a)y-1=0与直线l2:(a-1)x+(2a+3)y+2=0互相垂直.
【解析】 法一:(1)由l1:2x+(m+1)y+4=0,
l2:mx+3y-2=0知:①当m=0时,显然l1与l2不平行.
②当m≠0时,要使l1∥l2,需=≠.
解得m=2或m=-3,∴m的值为2或-3.
(2)由题意知,直线l1⊥l2.
①若1-a=0,即a=1时,直线l1:3x-1=0与直线l2:5y+2=0显然垂直.
②若2a+3=0,即a=-时,直线l1:x+5y-2=0与直线l2:5x-4=0不垂直.
③若1-a≠0且2a+3≠0,则直线l1,l2的斜率k1,k2都存在,k1=-,k2=-.
当l1⊥l2时,k1·k2=-1,
即·=-1,
∴a=-1.
综上可知,当a=1或a=-1时,直线l1⊥l2.
法二:(1)令2×3=m(m+1),
解得m=-3或m=2.
当m=-3时,l1:x-y+2=0,l2:3x-3y+2=0,
显然l1与l2不重合,∴l1∥l2.
同理当m=2时,l1:2x+3y+4=0,l2:2x+3y-2=0,
显然l1与l2不重合,∴l1∥l2,∴m的值为2或-3.
(2)由题意知直线l1⊥l2,
∴(a+2)(a-1)+(1-a)(2a+3)=0,解得a=±1,
将a=±1代入方程,均满足题意.
故当a=1或a=-1时,直线l1⊥l2.
例题7.不论为何值,直线恒过定点( )
A. B. C. D.
【答案】B【详解】
恒过定点,恒过定点,由解得即直线恒过定点.
例题8:已知△ABC的三个顶点坐标分别是A(1,-1),B(-1,3),C(3,0).
(1)判断△ABC的形状;
(2)求△ABC的面积.
【解析】(1)如图所示,△ABC为直角三角形,下面进行验证.
法一:∵|AB|==2,
|AC|==,|BC|==5.
∴|AB|2+|AC|2=|BC|2,即△ABC是以A为直角顶点的直角三角形.
法二:∵kAB==-2,kAC==.
∴kAB·kAC=-1,∴AB⊥AC.
∴△ABC是以A为直角顶点的直角三角形.
(2)由(1)中法一得|AB|=2,|AC|=.
又∵∠A=90°,∴S△ABC=|AB||AC|=×2×=5.
例题9.求点P(3,-2)到下列直线的距离:
①y=x+;②y=6;③x=4.
【解析】①把方程y=x+写成3x-4y+1=0,由点到直线的距离公式得d==.
②把方程y=6写成0·x+y-6=0,由点到直线的距离公式得d==8.
③因为直线x=4平行于y轴,
所以d=|4-3|=1.
例题10.已知直线l1过点A(0,1),l2过点B(5,0),如果l1∥l2,且l1与l2之间的距离为5,求l1,l2的方程.
【解析】当直线l1,l2斜率存在时,设直线l1、l2的斜率为k,由斜截式得l1的方程为y=kx+1,即kx-y+1=0,由点斜式得l2的方程为y=k(x-5),即kx-y-5k=0,在直线l1上取一点A(0,1),则点A到直线l2的距离d==5,∴25k2+10k+1=25k2+25,∴k=,
∴l1的方程为12x-5y+5=0,l2的方程为12x-5y-60=0.
若直线l1,l2的斜率不存在,则l1的方程为x=0,l2的方程为x=5,它们之间的距离为5,同样满足条件.
综上可知,满足条件的直线方程有两组,即l1:12x-5y+5=0,l2:12x-5y-60=0或l1:x=0,l2:x=5.
练习
1.直线,当变动时,所有直线恒过定点坐标为( )
A. B. C. D.
【答案】C【详解】把直线方程整理为,令,故,所以定点为,
2.已知点,在直线上,则的方程为( )
A. B.
C. D.
【答案】A【详解】根据截距式可得直线方程为:
即.
3.已知直线的方程为,则直线的倾斜角为( )
A. B. C. D.
【答案】D【详解】
因为直线的方程为,所以直线的斜率不存在,所以直线的倾斜角为,
4.若直线l过点且斜率,则l的方程为( )
A. B. C. D.
【答案】A【详解】
由点斜式可得直线方程为,整理得.故选:A.
5.已知斜率为的直线过直线与交点,则原点到直线的距离为( )
A. B. C. D.
【答案】A【详解】联立,,解得,
又直线斜率为,∴直线的方程为,即,
∴原点到直线的距离为.
6.已知两条直线,平行,则( )
A. B.或 C. D.或
【答案】D【详解】因为两条直线,平行,则,解得或.
7.直线的倾斜角为( )
A. B. C. D.
【答案】B【详解】将直线化为点斜式方程得,
所以直线的斜率为,
所以直线的倾斜角为.
8.直线的倾斜角为( )
A. B. C. D.
【答案】C【详解】
由可得直线的斜率为,设直线的倾斜角为,则,
因为,所以,
9.过点且斜率为的直线在轴上的截距是( )
A. B. C. D.
【答案】D【详解】所求直线方程为,该直线交轴于点,
因此,该直线在轴上的截距是.
10.在平面直角坐标系中,直线的倾斜角是( )
A. B. C. D.
【答案】C【详解】
直线即的倾斜角为,
11.斜率为,在x轴上截距为2的直线的一般式方程是( )
A. B. C. D.
【答案】C【详解】直线在轴上的截距为2,直线经过点(2,0),
又直线的斜率为,由直线的点斜式方程得直线的方程为,即,
故选:C.
12.直线l经过点,且与直线平行,则l的一般式方程为__________.
【答案】
【详解】因为直线经过点,且与直线平行,
所以可设直线l的方程为从而有,解得
13.已知直线l1:和l2:,且l1l2,则两直线l1和l2间的距离是_________.
【答案】【详解】
由题意知,,得,
解得,所以,
所以两直线间的距离为,
14.两条平行线之间的距离等于________.
【答案】2【详解】
由题意可得两平行线间的距离为
,
15.已知点A(-2,-2),B(a,2)且,则a的值为___________.
【答案】1或-5【详解】
∵点A(-2,-2),B(a,2),且或.
故答案为:1或-5.
16.直线必经过定点___________.
【答案】【详解】
由,得,
所以,解得,
即直线过定点.
17.设直线l过点A(-1,3),且和直线平行.
(1)求直线l的方程;
(2)设l与x轴相交于点B,求直线l绕点B逆时针旋转90°所得的直线方程.
【答案】(1)(2)
解:由题意得:直线l和直线平行
直线l的方程为:,解得:.
(2)l与x轴相交于点B(3,0)
直线l绕点B逆时针旋转90°所得的直线方程的斜率为:.
直线方程:,化简得:.
18.求满足下列条件的直线方程:
(1)过点,倾斜角为45°;(2)过两点.
【答案】
(1)
(2)
(1)所求直线方程为,即.
(2)所求直线方程为,即.
19.已知两点,.
(1)求直线AB的斜率k和倾斜角;
(2)求直线AB在y轴上的截距b.
【答案】
(1),
(2)
(1)根据题意,设直线AB的斜率为k,倾斜角为,
又由两点,,则,
则,因为所以,
(2)根据题意,直线AB的斜率,则其方程,
变形可得:,直线AB在y轴上的截距;
即.
20.已知的顶点.
(1)求边上的高所在直线的方程;
(2)求边上的中线所在直线的方程;
(3)的中位线与边平行,求所在直线的方程.
【答案】
(1)(2)(3)
(1)三角形的三个顶点是.
所以BC斜率为:,所以BC边上的高AD的斜率为:,BC边上的高AD所在直线的方程为:,即;
(2)顶点是则其中点,所以中线AP所在直线直线斜率,
所以中线AP所在直线方程为:,即.
(3)求出的中点,求出BC的斜率为:,由点斜式即可写出方程,即
21.的三个顶点是,,,求:
(1)边BC上的中线所在直线的方程;
(2)边BC的垂直平分线的方程.
【答案】(1)(2)
(1)解:BC的中点坐标为,
所以边BC上的中线的斜率为,
所以边BC上的中线所在直线的方程为.
(2)解:由(1)知BC的中点坐标,又,
所以边BC的垂直平分线的斜率为,
所以边BC的垂直平分线的方程为.
22.已知直线经过两点,问:当取何值时:
(1)与轴平行?(2)与轴平行?(3)的斜率为?
【答案】(1);(2);(3).
【详解】(1)当直线与轴平行时,直线的斜率为0,此时,得.
(2)当与轴平行时,直线不存在斜率,得.
(3)当的斜率为时,有,解得.
故当时,与轴平行;当时,与轴平行;当,的斜率为.
23.已知的三个顶点是
(1)求边的高所在直线方程;
(2)的面积
【答案】(1);(2)8.
【详解】(1)设边的高所在直线为,
由题知 则,
又点在直线上所以直线的方程为
即
(2)所在直线方程为: 即
点到的距离
又
则
24.已知直线;.
(1)若,求的值;
(2)若,且直线与直线之间的距离为,求、的值.
【答案】(1);(2)或.
【详解】(1)设直线的斜率分别为,则.
若,则,,
(2)若,则, ∴可以化简为,
又直线与直线的距离,或,综上:.
25.已知直线,求
(1)求直线l的斜率:
(2)若直线m与l平行,且过点,求直线m的方程.
【答案】(1);(2).
【详解】(1)由直线方程知:,即直线l的斜率为;
(2)由(1),根据直线m与l平行,且过点,则直线m:,
∴直线m一般形式为.
26.求原点到下列直线的距离:
(1) (2).
【答案】(1)(2)0
【详解】(1),(2)直线,则
27.求满足下列条件的直线方程.
(1)斜率为,经过点;(2)斜率为,在轴上的截距是;
(3)经过两点和;(4)经过两点和.
【答案】(1);(2);(3);(4).
【详解】(1)由题意可知直线的方程为,即为;
(2)由题意可知直线的方程为,即为;
(3)由题意可知直线的方程为,即为;
(4)由题意可知直线的方程为,即为.
28.三角形的三个顶点是,,.
(1)求边所在的直线方程;
(2)求边上的高所在的直线方程;
(3)求经过两边和中点的直线的方程.
【答案】(1);(2);(3).
【详解】(1)由,.可得边所在的直线方程是:,即.
(2)因为边上的高垂直于,(1)由已知
高所在的直线方程斜率为
又边上的高过点,
故所求直线方程为
故边上的高所在的直线方程是.
(3)经过两边和中点的直线平行于,
可设所求直线方程为.
由已知线段的中点为
.
解得:
故经过两边和中点的直线方程为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
