5.1.2 导数的概念及其几何意义 课件(共22张PPT) 2021-2022学年高二上学期数学人教A版(2019)选择性必修第二册
文档属性
| 名称 | 5.1.2 导数的概念及其几何意义 课件(共22张PPT) 2021-2022学年高二上学期数学人教A版(2019)选择性必修第二册 |  | |
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-06 09:12:15 | ||
图片预览






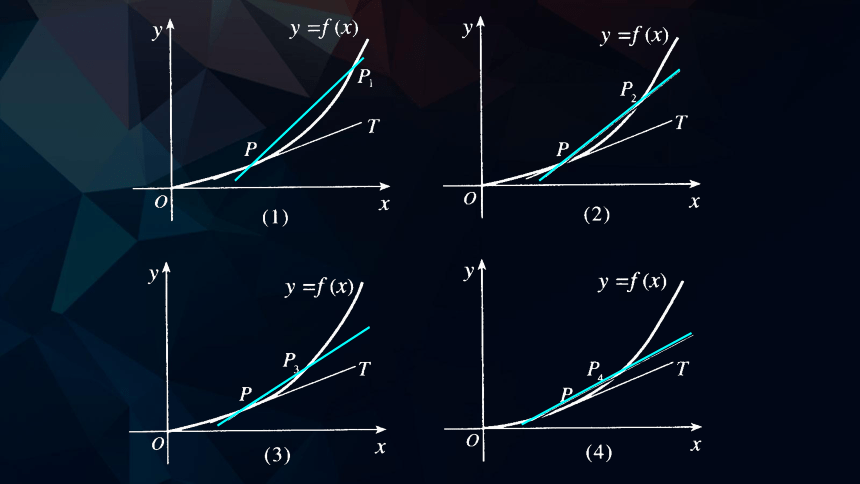


文档简介
(共22张PPT)
导数的概念及其几何意义
【温故知新】
【温故知新】
求函数y=f(x)的导数的一般步骤与方法:
【问题引入】
【新知探究】
如图, 当点Pn(xn, f(xn)) (n=1, 2, 3, 4)沿着曲线f(x)趋近于点P(x0,f(x0))时, 割线PPn的变化趋势是什么?
1、曲线在点P处的切线
当点Pn趋近于点P时,割线PPn趋近于确定的位置,这个确定位置的直线PT称为点P处的切线.
【例1】
导函数的定义
从求函数f(x)在x=x0处导数的过程可以看到,当x=x0时,f '(x0)是一个确定的数. 这样, 当x变化时, f '(x)便是x的一个函数, 我们称它为f(x)的导函数(简称导数).即:
【拓展练习1】
【小试牛刀】
1.判断正误. (正确的打“√”, 错误的打“×”)
(1)函数 y=f(x) 在某一点处的导数 f'(x0) 是一个常数. ( )
(2)函数 y=f(x)在点 x0 处的导数f'(x0)就是导函数f'(x)在点x= x0处的函数值. ( )
(3)函数f(x)=0没有导数. ( )
(4)直线与曲线相切,则直线与该曲线只有一个公共点. ( )
2. 如图, 直线l是曲线 y=f(x)在x=4处的切线, 则f'(4)= ( )
A. B. 3
C. 4 D. 5
3.已知函数f(x)的图像如图所示,f’(x)是f(x)的导函数,下列结论正确的是( )
A.0B.0C.0D.0【例4】
4.曲线 y=-2x2+x在点(1,-1)处的切线方程为
_____________.
【例5】
已知抛物线 y=2x2+1的切线分别满足下列条件, 求对应切点的坐标.
(1)切线的倾斜角为45°;
(2)切线平行于直线4x-y-2=0;
(3)切线垂直于直线x+8y-3=0.
【拓展练习2】
【拓展练习3】
【例6】
已知曲线C: f(x)=x3+x.
(1)求曲线C在点(1, 2)处切线的斜率;
(2)设曲线C上任意一点处切线的倾斜角为α, 求α的取值范围.
导数的概念及其几何意义
【温故知新】
【温故知新】
求函数y=f(x)的导数的一般步骤与方法:
【问题引入】
【新知探究】
如图, 当点Pn(xn, f(xn)) (n=1, 2, 3, 4)沿着曲线f(x)趋近于点P(x0,f(x0))时, 割线PPn的变化趋势是什么?
1、曲线在点P处的切线
当点Pn趋近于点P时,割线PPn趋近于确定的位置,这个确定位置的直线PT称为点P处的切线.
【例1】
导函数的定义
从求函数f(x)在x=x0处导数的过程可以看到,当x=x0时,f '(x0)是一个确定的数. 这样, 当x变化时, f '(x)便是x的一个函数, 我们称它为f(x)的导函数(简称导数).即:
【拓展练习1】
【小试牛刀】
1.判断正误. (正确的打“√”, 错误的打“×”)
(1)函数 y=f(x) 在某一点处的导数 f'(x0) 是一个常数. ( )
(2)函数 y=f(x)在点 x0 处的导数f'(x0)就是导函数f'(x)在点x= x0处的函数值. ( )
(3)函数f(x)=0没有导数. ( )
(4)直线与曲线相切,则直线与该曲线只有一个公共点. ( )
2. 如图, 直线l是曲线 y=f(x)在x=4处的切线, 则f'(4)= ( )
A. B. 3
C. 4 D. 5
3.已知函数f(x)的图像如图所示,f’(x)是f(x)的导函数,下列结论正确的是( )
A.0
4.曲线 y=-2x2+x在点(1,-1)处的切线方程为
_____________.
【例5】
已知抛物线 y=2x2+1的切线分别满足下列条件, 求对应切点的坐标.
(1)切线的倾斜角为45°;
(2)切线平行于直线4x-y-2=0;
(3)切线垂直于直线x+8y-3=0.
【拓展练习2】
【拓展练习3】
【例6】
已知曲线C: f(x)=x3+x.
(1)求曲线C在点(1, 2)处切线的斜率;
(2)设曲线C上任意一点处切线的倾斜角为α, 求α的取值范围.
