5.1.1变化率问题 课件(共22张PPT) 2021-2022学年高二上学期数学人教A版(2019)选择性必修第二册
文档属性
| 名称 | 5.1.1变化率问题 课件(共22张PPT) 2021-2022学年高二上学期数学人教A版(2019)选择性必修第二册 |

|
|
| 格式 | zip | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-06 00:00:00 | ||
图片预览








文档简介
(共22张PPT)
变化率问题
牛顿是17世纪的物理巨匠。 有一天,他观察到了一个现象:
一辆汽车按照路程与时间的关系: s=t2
向前行驶。
问题引入
牛顿
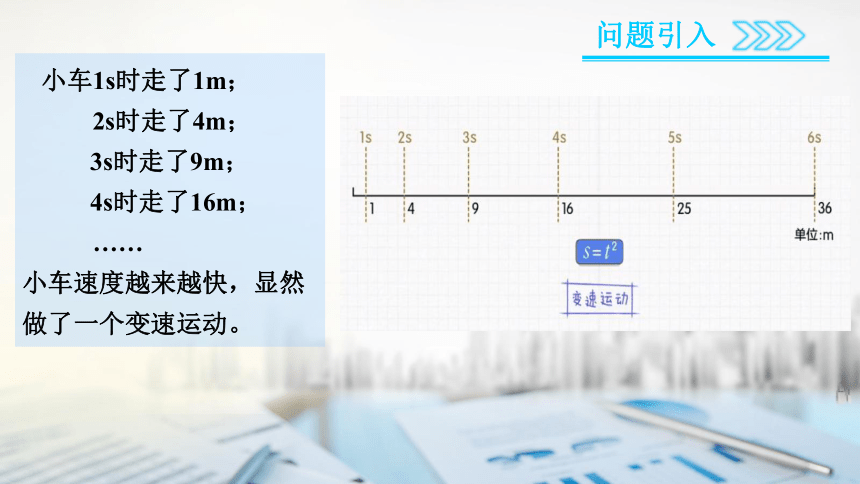
小车1s时走了1m;
2s时走了4m;
3s时走了9m;
4s时走了16m;
……
小车速度越来越快,显然做了一个变速运动。
问题引入
牛顿能很简单地计算出平均速度。比如:第5s到第6s,路程是25m到36m,它的平均速度是多少呢?
问题引入
牛顿能很简单地计算出平均速度。比如:第5s到第6s,路程是25m到36m,它的平均速度是多少呢?
问题引入
若函数关系用y=f(x)表示,则变化率可用式子
表示。这个式子称为函数 y=f(x) 从 x1 到 x2 的平均变化率。
习惯用 x=x1-x2, y=y1-y2 ,故平均变化率表示为:
牛顿能很简单地计算出平均速度。比如:第5s到第6s,路程是25m到36m,它的平均速度是多少呢?
问题引入
但天才的牛大爷并不满足于算出平均速度,他更想知道,在变速运动中,瞬时速度怎么算呢?
问题引入
从5s到6s,小车的速度变化了不少,用其平均速度来刻画5s时的瞬时速度,不够准确。那如果缩短时间,你能求出由5s到5.1s的平均速度吗?由5s到5.01s呢
问题引入
问题引入
(1)求5s到5.1s的平均速度
(2)求5s到5.01s的平均速度
由5s到5+ t s的平均速度又如何计算呢?
问题引入
由5s到5+ t s的平均速度又如何计算呢?
问题引入
当时间为 t 到 t +△t的平均速度的计算式子:
问题分析
当时间为 t 到 t +△t的平均速度的计算式子:
问题分析
当时间为 t 的瞬时速度的计算式子:
知识归纳
一般地,函数 在 处的瞬时变化率是
我们称它为函数 在 处的导数,记作 或 ,即
思考:
思考:
【例1】
已知质点M做直线运动,且位移随时间变化的函数为s=2t2+3(位移单位:cm,时间单位:s).
已知函数f(x)=2x2+3x-5.
(1)当x1=4且△x=1时, 求函数增量△y和平均变化率 ;
(2)当x1=4且△x=0.1时,求函数增量△y和平均变化率 ;
(3)分析(1)(2)中的平均变化率的几何意义.
【例2】
【例3】
求函数f(x)=3x2-2x在x=1处的导数.
【例4】
【课堂训练】
变化率问题
牛顿是17世纪的物理巨匠。 有一天,他观察到了一个现象:
一辆汽车按照路程与时间的关系: s=t2
向前行驶。
问题引入
牛顿
小车1s时走了1m;
2s时走了4m;
3s时走了9m;
4s时走了16m;
……
小车速度越来越快,显然做了一个变速运动。
问题引入
牛顿能很简单地计算出平均速度。比如:第5s到第6s,路程是25m到36m,它的平均速度是多少呢?
问题引入
牛顿能很简单地计算出平均速度。比如:第5s到第6s,路程是25m到36m,它的平均速度是多少呢?
问题引入
若函数关系用y=f(x)表示,则变化率可用式子
表示。这个式子称为函数 y=f(x) 从 x1 到 x2 的平均变化率。
习惯用 x=x1-x2, y=y1-y2 ,故平均变化率表示为:
牛顿能很简单地计算出平均速度。比如:第5s到第6s,路程是25m到36m,它的平均速度是多少呢?
问题引入
但天才的牛大爷并不满足于算出平均速度,他更想知道,在变速运动中,瞬时速度怎么算呢?
问题引入
从5s到6s,小车的速度变化了不少,用其平均速度来刻画5s时的瞬时速度,不够准确。那如果缩短时间,你能求出由5s到5.1s的平均速度吗?由5s到5.01s呢
问题引入
问题引入
(1)求5s到5.1s的平均速度
(2)求5s到5.01s的平均速度
由5s到5+ t s的平均速度又如何计算呢?
问题引入
由5s到5+ t s的平均速度又如何计算呢?
问题引入
当时间为 t 到 t +△t的平均速度的计算式子:
问题分析
当时间为 t 到 t +△t的平均速度的计算式子:
问题分析
当时间为 t 的瞬时速度的计算式子:
知识归纳
一般地,函数 在 处的瞬时变化率是
我们称它为函数 在 处的导数,记作 或 ,即
思考:
思考:
【例1】
已知质点M做直线运动,且位移随时间变化的函数为s=2t2+3(位移单位:cm,时间单位:s).
已知函数f(x)=2x2+3x-5.
(1)当x1=4且△x=1时, 求函数增量△y和平均变化率 ;
(2)当x1=4且△x=0.1时,求函数增量△y和平均变化率 ;
(3)分析(1)(2)中的平均变化率的几何意义.
【例2】
【例3】
求函数f(x)=3x2-2x在x=1处的导数.
【例4】
【课堂训练】
