青岛版数学九年级上册 4.1一元二次方程(2) 课件(共18张PPT)
文档属性
| 名称 | 青岛版数学九年级上册 4.1一元二次方程(2) 课件(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 297.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-03 12:13:31 | ||
图片预览




文档简介
(共18张PPT)
2.1一元二次方程(2)
1.经历对一元二次方程根的探索过程并理解其意义.(重点)
3.会估算一元二次方程的根.(难点)
学习目标
问1:一元二次方程有哪些特点?
① 只含有一个未知数;
②未知数的最高次项系数是2;
③整式方程
问2:一元二次方程的一般形式是什么?
ax2 +bx + c = 0(a , b , c为常数, a≠0)
复习引入
导入新课
问题1:在上一课中,我们知道四周未铺地毯部分的宽度x满足方程(8 -2x)(5-2x)= 18,你能求出这个宽度吗?
(1) x可能小于0吗 说说你的理由.
(2) x可能大于4吗 可能大于2.5吗
说说你的理由.
一元二次方程根的估算
讲授新课
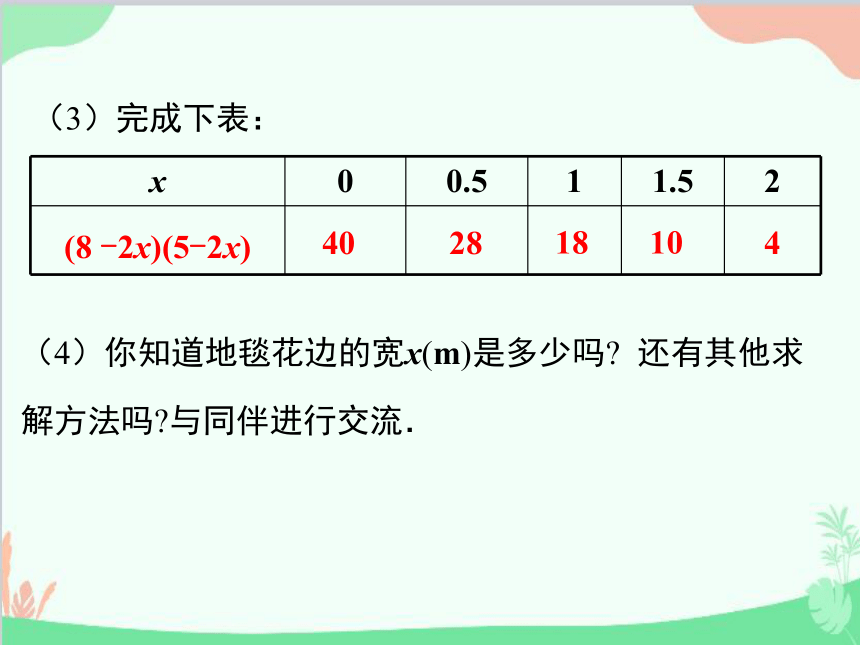
(3)完成下表:
x 0 0.5 1 1.5 2
(8 -2x)(5-2x)
(4)你知道地毯花边的宽x(m)是多少吗 还有其他求解方法吗 与同伴进行交流.
4
10
18
28
40
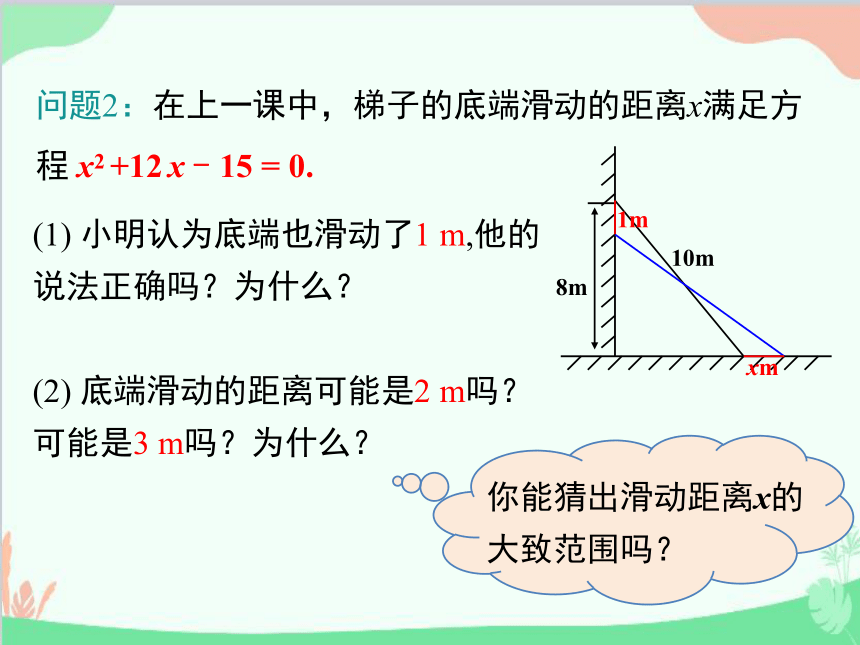
问题2:在上一课中,梯子的底端滑动的距离x满足方程 x2 +12 x - 15 = 0.
10m
8m
1m
xm
你能猜出滑动距离x的大致范围吗?
(1) 小明认为底端也滑动了1 m,他的
说法正确吗?为什么?
(2) 底端滑动的距离可能是2 m吗?
可能是3 m吗?为什么?
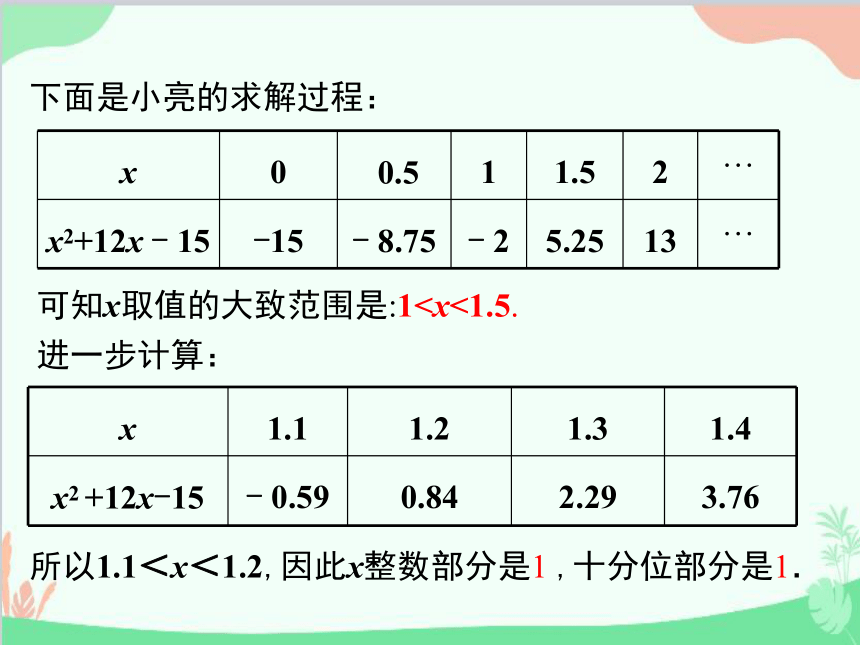
下面是小亮的求解过程:
x 0 0.5 1 1.5 2 …
x2+12x - 15 -15 - 8.75 - 2 5.25 13 …
可知x取值的大致范围是:1进一步计算:
所以1.1<x<1.2,因此x整数部分是1 ,十分位部分是1.
x 1.1 1.2 1.3 1.4
x2 +12x-15 - 0.59 0.84 2.29 3.76
用“两边夹”思想解一元二次方程的步骤:
(1)估计一个大致范围;
(2)取中间值(靠近一端的值)缩小范围,直到确定出个位上的数字;
(3)继续取值缩小范围,确定十分位上的数字;
(4)继续取值缩小范围,确定百分位上的数字……需要注意,如果不要求精确度,估计时还可以进行下去.用“夹逼法”求一元二次方程的根时,一般都要确定根的近似值的精确度.
规律方法 上述求解是利用了“两边夹”的思想.
归纳总结
例2:一名跳水运动员进行10m跳台跳水训练,在正常情况下,运动员必需在距水面5m以前完成规定的翻腾动作,并且调整好入水姿势,否则就容易出现失误.假设运动员起跳后的运动时间t(s)和运动员距水面的高度h(m)满足关系: h=10+2.5t-5t2. 那么他最多有多长时间完成规定动作?
5=10+2.5t-5t2.
2t2-t-2=0.
即
解:根据题意得
完成下表(在0根据题意,t的取值范围大致是0完成下表(在0由此看出,可以使2t2-t-2的值为0的t的范围是1.2t … …
2t2-t-2 … …
0 1 1.1 1.2 1.3 1.4 2 3
-2 -1 -0.68 -0.32 0.08 0.52 4 13
根据题意,t的取值范围大致是01.请求出一元二次方程 x2 - 2x - 1=0的正数根(精确到0.1).
解:(1)列表.依次取x=0,1,2,3,…
由上表可发现,当2<x<3时, -1< x2 - 2x -1 <2;
x 0 1 2 3 …
x2 - 2x - 1 -1 -2 -1 2 …
随堂练习
(2)继续列表,依次取x=2.1,2.2,2.3,2.4,2.5,…
由表发现,当2.4<x<2.5时,-0.04< x2 -2x-1<0.25;
(3)取x=2.45,则x2 - 2x - 1≈0.1025.
∴2.4<x<2.45,
∴x≈2.4.
x 2.2 2.3 2.4 2.5 …
x2 - 2x - 1 -0.79 -0.31 -0.04 0.25 …
2.根据题意,列出方程,并估算方程的解:
一面积为120m2的矩形苗圃,它的长比宽多2m,苗圃的长和宽各是多少?
解:设苗圃的宽为x m,则长为(x+2) m ,
根据题意,得 x (x + 2) = 120.
即 x2 + 2x - 120 = 0.
120m2
(x+2)m
xm
根据题意,x的取值范围大致是0 < x < 11.
根据题意,x的取值范围大致是0 < x < 11.
解方程 x2 + 2x - 120 = 0.
完成下表(在0 < x < 11这个范围内取值计算,逐步逼近):
x … …
x2 +2x – 120 … …
8 9 10 11
-40 -21 0 23
所以x=10.因此这苗圃的长是12米,宽是10米.
3.若关于x的一元二次方程(m+2)x2+5x+m2-4=0
有一个根为0,求m的值.
二次项系数不为零不容忽视
解:将x=0代入方程m2-4=0,
解得m= ±2.
∵ m+2 ≠0,
∴ m ≠-2,
综上所述:m =2.
拓广探索
已知关于x的一元二次方程 ax2+bx+c=0 (a≠0)一个根为1, 求a+b+c的值.
解:由题意,得
思考:1.若 a+b+c=0,你能通过观察,求出方程ax2+bx+c=0 (a≠0)的一个根吗
解:由题意,得
∴方程ax2+bx+c=0 (a≠0)的一个根是1.
2. 若 a-b +c=0,4a+2b +c=0 ,你能通过观察,求出方程ax2+bx+c=0 (a≠0)的一个根吗
x=2
解一元二次方程
(“两边夹”方法)
确定其解的大致范围
列表、计算
进行两边“夹逼”
……
求得近似解
课堂小结
2.1一元二次方程(2)
1.经历对一元二次方程根的探索过程并理解其意义.(重点)
3.会估算一元二次方程的根.(难点)
学习目标
问1:一元二次方程有哪些特点?
① 只含有一个未知数;
②未知数的最高次项系数是2;
③整式方程
问2:一元二次方程的一般形式是什么?
ax2 +bx + c = 0(a , b , c为常数, a≠0)
复习引入
导入新课
问题1:在上一课中,我们知道四周未铺地毯部分的宽度x满足方程(8 -2x)(5-2x)= 18,你能求出这个宽度吗?
(1) x可能小于0吗 说说你的理由.
(2) x可能大于4吗 可能大于2.5吗
说说你的理由.
一元二次方程根的估算
讲授新课
(3)完成下表:
x 0 0.5 1 1.5 2
(8 -2x)(5-2x)
(4)你知道地毯花边的宽x(m)是多少吗 还有其他求解方法吗 与同伴进行交流.
4
10
18
28
40
问题2:在上一课中,梯子的底端滑动的距离x满足方程 x2 +12 x - 15 = 0.
10m
8m
1m
xm
你能猜出滑动距离x的大致范围吗?
(1) 小明认为底端也滑动了1 m,他的
说法正确吗?为什么?
(2) 底端滑动的距离可能是2 m吗?
可能是3 m吗?为什么?
下面是小亮的求解过程:
x 0 0.5 1 1.5 2 …
x2+12x - 15 -15 - 8.75 - 2 5.25 13 …
可知x取值的大致范围是:1
所以1.1<x<1.2,因此x整数部分是1 ,十分位部分是1.
x 1.1 1.2 1.3 1.4
x2 +12x-15 - 0.59 0.84 2.29 3.76
用“两边夹”思想解一元二次方程的步骤:
(1)估计一个大致范围;
(2)取中间值(靠近一端的值)缩小范围,直到确定出个位上的数字;
(3)继续取值缩小范围,确定十分位上的数字;
(4)继续取值缩小范围,确定百分位上的数字……需要注意,如果不要求精确度,估计时还可以进行下去.用“夹逼法”求一元二次方程的根时,一般都要确定根的近似值的精确度.
规律方法 上述求解是利用了“两边夹”的思想.
归纳总结
例2:一名跳水运动员进行10m跳台跳水训练,在正常情况下,运动员必需在距水面5m以前完成规定的翻腾动作,并且调整好入水姿势,否则就容易出现失误.假设运动员起跳后的运动时间t(s)和运动员距水面的高度h(m)满足关系: h=10+2.5t-5t2. 那么他最多有多长时间完成规定动作?
5=10+2.5t-5t2.
2t2-t-2=0.
即
解:根据题意得
完成下表(在0
2t2-t-2 … …
0 1 1.1 1.2 1.3 1.4 2 3
-2 -1 -0.68 -0.32 0.08 0.52 4 13
根据题意,t的取值范围大致是0
解:(1)列表.依次取x=0,1,2,3,…
由上表可发现,当2<x<3时, -1< x2 - 2x -1 <2;
x 0 1 2 3 …
x2 - 2x - 1 -1 -2 -1 2 …
随堂练习
(2)继续列表,依次取x=2.1,2.2,2.3,2.4,2.5,…
由表发现,当2.4<x<2.5时,-0.04< x2 -2x-1<0.25;
(3)取x=2.45,则x2 - 2x - 1≈0.1025.
∴2.4<x<2.45,
∴x≈2.4.
x 2.2 2.3 2.4 2.5 …
x2 - 2x - 1 -0.79 -0.31 -0.04 0.25 …
2.根据题意,列出方程,并估算方程的解:
一面积为120m2的矩形苗圃,它的长比宽多2m,苗圃的长和宽各是多少?
解:设苗圃的宽为x m,则长为(x+2) m ,
根据题意,得 x (x + 2) = 120.
即 x2 + 2x - 120 = 0.
120m2
(x+2)m
xm
根据题意,x的取值范围大致是0 < x < 11.
根据题意,x的取值范围大致是0 < x < 11.
解方程 x2 + 2x - 120 = 0.
完成下表(在0 < x < 11这个范围内取值计算,逐步逼近):
x … …
x2 +2x – 120 … …
8 9 10 11
-40 -21 0 23
所以x=10.因此这苗圃的长是12米,宽是10米.
3.若关于x的一元二次方程(m+2)x2+5x+m2-4=0
有一个根为0,求m的值.
二次项系数不为零不容忽视
解:将x=0代入方程m2-4=0,
解得m= ±2.
∵ m+2 ≠0,
∴ m ≠-2,
综上所述:m =2.
拓广探索
已知关于x的一元二次方程 ax2+bx+c=0 (a≠0)一个根为1, 求a+b+c的值.
解:由题意,得
思考:1.若 a+b+c=0,你能通过观察,求出方程ax2+bx+c=0 (a≠0)的一个根吗
解:由题意,得
∴方程ax2+bx+c=0 (a≠0)的一个根是1.
2. 若 a-b +c=0,4a+2b +c=0 ,你能通过观察,求出方程ax2+bx+c=0 (a≠0)的一个根吗
x=2
解一元二次方程
(“两边夹”方法)
确定其解的大致范围
列表、计算
进行两边“夹逼”
……
求得近似解
课堂小结
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
