湘教版>九年级下册 2.1圆的对称性(共32张)
文档属性
| 名称 | 湘教版>九年级下册 2.1圆的对称性(共32张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-03 00:00:00 | ||
图片预览











文档简介
(共32张PPT)
2.1 圆的对称性
第2章 圆
知识点
圆
知1-讲
1
1. 圆的定义
(1)静态定义:圆是平面内到一定点的距离等于定长的所有点组成的图形,这个定点叫作圆心,定长叫作半径.
(2)动态定义:圆也可以看成是平面内一个动点绕一个定点旋转一周所形成的图形,定点叫作圆心,定点与动点的连线段叫作半径.
知1-讲
2. 圆的表示法:以点O 为圆心的圆叫作圆O,记作⊙ O.
3. 圆的特性
(1)圆上各点到定点(圆心O)的距离都等于定长(半径r), 即同圆的半径相等.
(2)到定点的距离等于定长的点都在同一个圆上,即到圆心的距离等于半径的点在圆上.
知1-讲
特别提醒:
1.确定一个圆需要“两个要素”,一是圆心:圆心定其位置,二是半径:半径定其大小.
2.圆是一条封闭的曲线,曲线是“圆周”,而不能认为是“圆面”.
3. “圆上的点”指圆周上的点.
知1-讲
例 1
下列说法中, 错误的有( )
(1)经过点P 的圆有无数个;
(2)以点P 为圆心的圆有无数个;
(3)半径为3 cm 且经过点P 的圆有无数个;
(4)以点P 为圆心,3 cm 长为半径的圆有无数个.
A. 1 个 B. 2 个 C. 3 个 D. 4 个
A
知1-讲
解题秘方:紧扣圆的定义的“两要素”进行判断.
特别提醒:
1. 圆的两种定义中确定圆的条件是相同的,即圆心和半径,两者缺一不可;
2.“点在圆上”和“圆过点”表示的意义都是:这个点在圆周上.
知1-讲
解:确定一个圆必须有两个条件,即圆心和半径,只满足一个条件或不满足任何一个条件的圆都有无数个,由此可知(1)(2)(3)正确;
圆心和半径都确定,这样的圆有且只有一个(唯一),由此可知(4)错误.
知1-讲
菱形ABCD 的对角线AC 和BD 相交于点O. E,F,G,H 分别为边AB,BC,CD,DA 的中点,那么点E,F,G,H 是否在同一个圆上?请说明理由.
例2
知1-讲
解题秘方:只需说明E,F,G,H 四点到点O 的距离相等.
解法提醒:
本题运用数形结合思想,将说明“位置关系”转化为说明“数量关系”.即将求证几个点在同一个圆上转化为证明这几个点到某点(圆心)的距离相等“. 到定点的距离相等(数量关系)的点在同一个圆上(位置关系)”是证明多点共圆问题的常用方法.
知1-讲
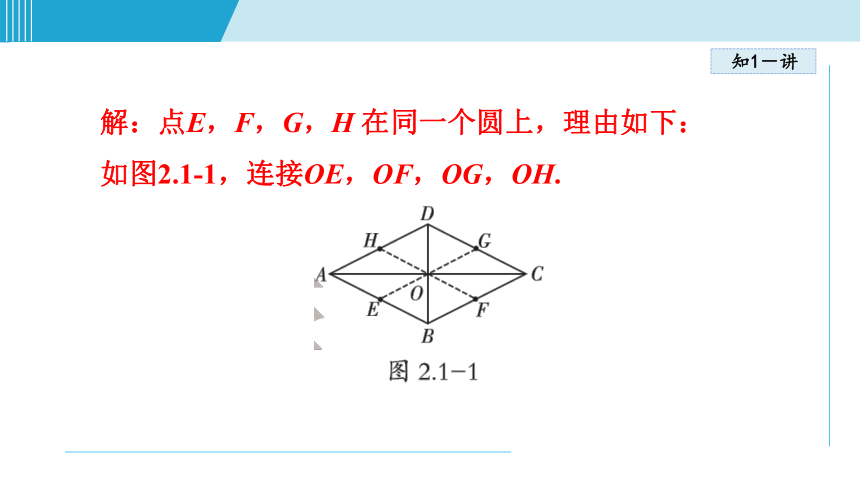
解:点E,F,G,H 在同一个圆上,理由如下:
如图2.1-1,连接OE,OF,OG,OH.
知1-讲
∵四边形ABCD 是菱形,
∴ AB=BC=CD=DA,AC⊥BD.
又∵ E为AB边的中点,∴ OE= AB.
同理可得,OF= BC,OG= CD,OH= DA.
∴ OE=OF=OG=OH.
∴点E,F,G,H 在以点O为圆心,OE为半径的圆上.
知2-讲
知识点
点与圆的位置关系
2
1. 把到圆心的距离小于半径的点叫作圆内的点;到圆心的距离大于半径的点叫作圆外的点.
知2-讲
2. 点与圆的位置关系
设⊙ O 的半径为r,点P 到圆心的距离OP=d,则有:
点和圆的位置关系 特点 等价关系
点在圆外 点到圆心的距离大于半径 点P在圆外d>r
点在圆上 点到圆心的距离等于半径 点P在圆上d=r
点在圆内 点到圆心的距离小于半径 点P在圆内d<r
知2-讲
特别提醒 符号“ ”读作“等价于”,它表示从符号的左端可以推出右端,从右端也可以推出左端,即左右两端互为因果关系.
知2-讲
拓宽视野:
圆的外部可以看成到圆心的距离大于半径的点的集合;
圆上可以看成到圆心的距离等于半径的点的集合;
圆的内部可以看成到圆心的距离小于半径的点的集合.
知2-讲
已知⊙ O 的半径r=5 cm,圆心O到直线l 的距离d=OD=3 cm,在直线l 上有P,Q,R三点,且有PD=4 cm,QD=5 cm,RD=3 cm,那么P,Q,R 三点与⊙ O 的位置关系各是怎样的?
例 3
解题秘方:比较点到圆心的距离与半径的大小确定点的位置情况.
知2-讲
解:如图2.1-2,连接OR,OP,OQ.
∵ PD=4 cm,OD=3 cm,且OD ⊥ l,
∴ OP= =5 (cm)=r.
∴点P 在⊙ O 上.
知2-讲
∵ QD=5 cm,
∴ OQ= = (cm)>5 cm=r,
∴点Q 在⊙ O 外.
∵ RD=3 cm,
∴ OR= = (cm)<5 cm=r.
∴点R在⊙ O内.
知2-讲
解法巧记:
点与圆的位置关系,
d,r 关系是关键,
d 小于r 在圆内,
d 等于r 在圆上,
d 大于r 在圆外.
知识点
圆的有关概念
知3-讲
3
定义 注意
弦 连接圆上任意两点的线段叫作弦 圆中有无数条弦,其中直径是最长的弦
直径 经过圆心的弦叫作直径
知3-讲
弧、半圆、
劣弧、优弧、 (1)圆上任意两点间的部分叫作圆弧,简称弧;
(2)圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫作半圆;
(3)小于半圆的弧叫作劣弧;
(4)大于半圆的弧叫作优弧 弧包括优弧、劣弧和半圆;半圆既不是劣弧,也不是优弧
知3-讲
等圆 能够重合的两个圆叫作等圆.容易看出:半径相等的两个圆是等圆;反过来,同圆或等圆的半径相等 等圆只和半径的大小有关,和圆心的位置无关
等弧 能够互相重合的弧叫作等弧 等弧只能出现在同圆或等圆中;等弧是全等的,而不仅仅是弧的长度相等
知3-讲
特别提醒:
1. 弦与直径的关系:直径是过圆心(或最长)的弦,但弦不一定是直径.
2. 弧与半圆的关系:半圆是弧,但弧不一定是半圆.
3. 弦与弧的关系:
(1)弦是圆上两点间的线段,有无数条;弧是圆上两点间的部分,是曲线,也有无数条.
(2)每条弧对一条弦;而每条弦对的弧有两条: 一条优弧、一条劣弧或两个半圆.
知3-讲
下列语句中正确的有( )
①直径是弦;②弦是直径;③半径相等的两个半圆是等弧;④长度相等的两条弧是等弧;⑤半圆是弧,弧不一定是半圆.
A. 1 个 B. 2 个 C. 3 个 D. 4 个
C
例4
警示误区:
只有在同圆或等圆中才可能有等弧,等弧长度一定相等,但长度相等的弧不一定是等弧.
弧不仅有长度,还有度数,规定:半圆的度数为180°,劣弧的度数小于180°,优弧的度数大于180° .
知3-讲
解题秘方:紧扣圆的相关概念进行解答.
知3-讲
解:直径是最长的弦,故①正确;直径是过圆心的弦,但弦不一定是直径,故②错误;半圆是弧,半径相等的两个半圆能互相重合,所以是等弧,故③正确;只有在同圆或等圆中,长度相等的两条弧才是等弧,故④错误;弧分为劣弧、优弧、半圆,故⑤正确.
知4-讲
知识点
圆的对称性
4
1. 圆是中心对称图形,圆心是它的对称中心.
2. 圆是轴对称图形,任意一条直径所在的直线都是圆的对称轴.
(1)圆的对称轴有无数条.
(2)“圆的对称轴是直径所在的直线”或说成“圆的对称轴是经过圆心的直线”
警示误区:
因为直径是弦,弦是线段,而对称轴是直线,所以不能说“圆的对称轴是直径”.
知4-讲
[模拟·雅安] 如图2.1-3 的图形中,不是轴对称图形的是( )
例 5
B
知4-讲
解题秘方:由于圆的特殊轴对称性,只需判断圆内图形是否是以过圆心的直线为对称轴的轴对称图形即可.
知4-讲
解:A. 是轴对称图形,A 不合题意;
B. 不是轴对称图形,B 符合题意;
C. 是轴对称图形,C 不合题意;
D. 是轴对称图形,D 不合题意.
知4-讲
知识储备:
判断一个图形是不是轴对称图形,关键看能否找到一条直线,使得沿着这条直线折叠,直线两旁部分能够互相重合,若能,这个图形是轴对称图形;否则不是.
圆的对称性
圆
两要素
相关概念
圆心
半径
弦(直径)
弦(半圆)
等圆(等弧)
对称性
与点的关系
相关概念
相关概念
位置
大小
2.1 圆的对称性
第2章 圆
知识点
圆
知1-讲
1
1. 圆的定义
(1)静态定义:圆是平面内到一定点的距离等于定长的所有点组成的图形,这个定点叫作圆心,定长叫作半径.
(2)动态定义:圆也可以看成是平面内一个动点绕一个定点旋转一周所形成的图形,定点叫作圆心,定点与动点的连线段叫作半径.
知1-讲
2. 圆的表示法:以点O 为圆心的圆叫作圆O,记作⊙ O.
3. 圆的特性
(1)圆上各点到定点(圆心O)的距离都等于定长(半径r), 即同圆的半径相等.
(2)到定点的距离等于定长的点都在同一个圆上,即到圆心的距离等于半径的点在圆上.
知1-讲
特别提醒:
1.确定一个圆需要“两个要素”,一是圆心:圆心定其位置,二是半径:半径定其大小.
2.圆是一条封闭的曲线,曲线是“圆周”,而不能认为是“圆面”.
3. “圆上的点”指圆周上的点.
知1-讲
例 1
下列说法中, 错误的有( )
(1)经过点P 的圆有无数个;
(2)以点P 为圆心的圆有无数个;
(3)半径为3 cm 且经过点P 的圆有无数个;
(4)以点P 为圆心,3 cm 长为半径的圆有无数个.
A. 1 个 B. 2 个 C. 3 个 D. 4 个
A
知1-讲
解题秘方:紧扣圆的定义的“两要素”进行判断.
特别提醒:
1. 圆的两种定义中确定圆的条件是相同的,即圆心和半径,两者缺一不可;
2.“点在圆上”和“圆过点”表示的意义都是:这个点在圆周上.
知1-讲
解:确定一个圆必须有两个条件,即圆心和半径,只满足一个条件或不满足任何一个条件的圆都有无数个,由此可知(1)(2)(3)正确;
圆心和半径都确定,这样的圆有且只有一个(唯一),由此可知(4)错误.
知1-讲
菱形ABCD 的对角线AC 和BD 相交于点O. E,F,G,H 分别为边AB,BC,CD,DA 的中点,那么点E,F,G,H 是否在同一个圆上?请说明理由.
例2
知1-讲
解题秘方:只需说明E,F,G,H 四点到点O 的距离相等.
解法提醒:
本题运用数形结合思想,将说明“位置关系”转化为说明“数量关系”.即将求证几个点在同一个圆上转化为证明这几个点到某点(圆心)的距离相等“. 到定点的距离相等(数量关系)的点在同一个圆上(位置关系)”是证明多点共圆问题的常用方法.
知1-讲
解:点E,F,G,H 在同一个圆上,理由如下:
如图2.1-1,连接OE,OF,OG,OH.
知1-讲
∵四边形ABCD 是菱形,
∴ AB=BC=CD=DA,AC⊥BD.
又∵ E为AB边的中点,∴ OE= AB.
同理可得,OF= BC,OG= CD,OH= DA.
∴ OE=OF=OG=OH.
∴点E,F,G,H 在以点O为圆心,OE为半径的圆上.
知2-讲
知识点
点与圆的位置关系
2
1. 把到圆心的距离小于半径的点叫作圆内的点;到圆心的距离大于半径的点叫作圆外的点.
知2-讲
2. 点与圆的位置关系
设⊙ O 的半径为r,点P 到圆心的距离OP=d,则有:
点和圆的位置关系 特点 等价关系
点在圆外 点到圆心的距离大于半径 点P在圆外d>r
点在圆上 点到圆心的距离等于半径 点P在圆上d=r
点在圆内 点到圆心的距离小于半径 点P在圆内d<r
知2-讲
特别提醒 符号“ ”读作“等价于”,它表示从符号的左端可以推出右端,从右端也可以推出左端,即左右两端互为因果关系.
知2-讲
拓宽视野:
圆的外部可以看成到圆心的距离大于半径的点的集合;
圆上可以看成到圆心的距离等于半径的点的集合;
圆的内部可以看成到圆心的距离小于半径的点的集合.
知2-讲
已知⊙ O 的半径r=5 cm,圆心O到直线l 的距离d=OD=3 cm,在直线l 上有P,Q,R三点,且有PD=4 cm,QD=5 cm,RD=3 cm,那么P,Q,R 三点与⊙ O 的位置关系各是怎样的?
例 3
解题秘方:比较点到圆心的距离与半径的大小确定点的位置情况.
知2-讲
解:如图2.1-2,连接OR,OP,OQ.
∵ PD=4 cm,OD=3 cm,且OD ⊥ l,
∴ OP= =5 (cm)=r.
∴点P 在⊙ O 上.
知2-讲
∵ QD=5 cm,
∴ OQ= = (cm)>5 cm=r,
∴点Q 在⊙ O 外.
∵ RD=3 cm,
∴ OR= = (cm)<5 cm=r.
∴点R在⊙ O内.
知2-讲
解法巧记:
点与圆的位置关系,
d,r 关系是关键,
d 小于r 在圆内,
d 等于r 在圆上,
d 大于r 在圆外.
知识点
圆的有关概念
知3-讲
3
定义 注意
弦 连接圆上任意两点的线段叫作弦 圆中有无数条弦,其中直径是最长的弦
直径 经过圆心的弦叫作直径
知3-讲
弧、半圆、
劣弧、优弧、 (1)圆上任意两点间的部分叫作圆弧,简称弧;
(2)圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫作半圆;
(3)小于半圆的弧叫作劣弧;
(4)大于半圆的弧叫作优弧 弧包括优弧、劣弧和半圆;半圆既不是劣弧,也不是优弧
知3-讲
等圆 能够重合的两个圆叫作等圆.容易看出:半径相等的两个圆是等圆;反过来,同圆或等圆的半径相等 等圆只和半径的大小有关,和圆心的位置无关
等弧 能够互相重合的弧叫作等弧 等弧只能出现在同圆或等圆中;等弧是全等的,而不仅仅是弧的长度相等
知3-讲
特别提醒:
1. 弦与直径的关系:直径是过圆心(或最长)的弦,但弦不一定是直径.
2. 弧与半圆的关系:半圆是弧,但弧不一定是半圆.
3. 弦与弧的关系:
(1)弦是圆上两点间的线段,有无数条;弧是圆上两点间的部分,是曲线,也有无数条.
(2)每条弧对一条弦;而每条弦对的弧有两条: 一条优弧、一条劣弧或两个半圆.
知3-讲
下列语句中正确的有( )
①直径是弦;②弦是直径;③半径相等的两个半圆是等弧;④长度相等的两条弧是等弧;⑤半圆是弧,弧不一定是半圆.
A. 1 个 B. 2 个 C. 3 个 D. 4 个
C
例4
警示误区:
只有在同圆或等圆中才可能有等弧,等弧长度一定相等,但长度相等的弧不一定是等弧.
弧不仅有长度,还有度数,规定:半圆的度数为180°,劣弧的度数小于180°,优弧的度数大于180° .
知3-讲
解题秘方:紧扣圆的相关概念进行解答.
知3-讲
解:直径是最长的弦,故①正确;直径是过圆心的弦,但弦不一定是直径,故②错误;半圆是弧,半径相等的两个半圆能互相重合,所以是等弧,故③正确;只有在同圆或等圆中,长度相等的两条弧才是等弧,故④错误;弧分为劣弧、优弧、半圆,故⑤正确.
知4-讲
知识点
圆的对称性
4
1. 圆是中心对称图形,圆心是它的对称中心.
2. 圆是轴对称图形,任意一条直径所在的直线都是圆的对称轴.
(1)圆的对称轴有无数条.
(2)“圆的对称轴是直径所在的直线”或说成“圆的对称轴是经过圆心的直线”
警示误区:
因为直径是弦,弦是线段,而对称轴是直线,所以不能说“圆的对称轴是直径”.
知4-讲
[模拟·雅安] 如图2.1-3 的图形中,不是轴对称图形的是( )
例 5
B
知4-讲
解题秘方:由于圆的特殊轴对称性,只需判断圆内图形是否是以过圆心的直线为对称轴的轴对称图形即可.
知4-讲
解:A. 是轴对称图形,A 不合题意;
B. 不是轴对称图形,B 符合题意;
C. 是轴对称图形,C 不合题意;
D. 是轴对称图形,D 不合题意.
知4-讲
知识储备:
判断一个图形是不是轴对称图形,关键看能否找到一条直线,使得沿着这条直线折叠,直线两旁部分能够互相重合,若能,这个图形是轴对称图形;否则不是.
圆的对称性
圆
两要素
相关概念
圆心
半径
弦(直径)
弦(半圆)
等圆(等弧)
对称性
与点的关系
相关概念
相关概念
位置
大小
