湘教版九年级下册 2.2.1圆心角 课件(共18张)
文档属性
| 名称 | 湘教版九年级下册 2.2.1圆心角 课件(共18张) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-03 14:11:58 | ||
图片预览






文档简介
(共18张PPT)
2.2 圆心角、圆周角
第2章 圆
2.2.1 圆心角
知识点
圆的旋转不变性、圆心角
知1-讲
1
1. 圆的旋转不变性
圆是中心对称图形,圆心就是它的对称中心. 圆具有旋转不变性,把圆绕圆心旋转任意一个角度,所得的图形都与原图形重合.
知1-讲
2. 圆心角
顶点在圆心,角的两边与圆相交,像这样的角叫作圆心角,如图2.2-1,∠AOB是AB所对的圆心角,AB是∠AOB所对的弧. 注意一条弧所对的圆心角只有一个.
︵
︵
知1-讲
特别提醒:
圆心角的条件:
1. 顶点在圆心;
2. 两条边和圆相交.
其中“顶点在圆心”是圆心角的必备条件.
知1-讲
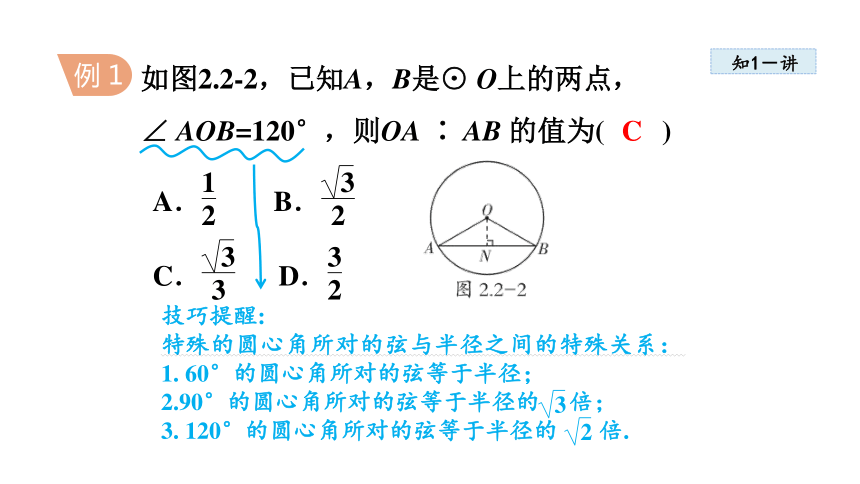
例 1
如图2.2-2,已知A,B是⊙ O上的两点,
∠ AOB=120°,则OA ∶ AB 的值为( )
C
技巧提醒:
特殊的圆心角所对的弦与半径之间的特殊关系:
1. 60°的圆心角所对的弦等于半径;
2.90°的圆心角所对的弦等于半径的 倍;
3. 120°的圆心角所对的弦等于半径的 倍.
知1-讲
解题秘方:紧扣圆心角的定义,将圆心角转化为等腰三角形的顶角,利用等腰三角形的性质探究半径与弦之间的关系.
知1-讲
解:如图2.2-2,过点O作ON⊥ AB于点N.
∵ OA=OB,∴ AN= AB.
∵∠AOB=120°,OA=OB,∴∠ A=30° .
设ON=a,则OA=2a,
∵ OA2-ON2=AN2,
∴ AN= a. ∴ AB=2 a.
∴ OA ∶ AB=2a ∶2 a= .
知2-讲
知识点
弧、弦、圆心角之间的关系
2
1. 关系
在同圆或等圆中,如果圆心角相等,那么它们所对的弧相等,所对的弦也相等.
警示误区:
不能忽略在同圆或等圆中这个前提,如果丢掉了这个前提,即使圆心角相等,所对的弧、弦也不一定相等.如图2.2-4,两个圆的圆心相同,AB与A′B′对应的圆心角相等,但AB≠A′B′,AB ≠A′B′.
︵
︵
︵
︵
知2-讲
2. 示例:弧、弦、圆心角的关系
如图2.2-3,若∠ AOB= ∠ A′OB′,则AB = A′B′,AB=A′B′
︵
︵
知2-讲
如图2.2-5,AB,CD 是⊙ O 的两条直径,弦CE ∥ AB,求证:BC = AE .
解题秘方:构造圆心角,利用“在同圆中,相等的圆心角所对的弧相等”证明.
例2
︵
︵
知2-讲
证明:如图2.2-5,连接OE.
∵ OE=OC,∴∠C= ∠E.
∵ CE∥AB,
∴∠C=∠BOC,∠E=∠AOE.
∴∠BOC=∠AOE.
∴BC = AE .
︵
︵
知2-讲
技巧提醒:
由例2的结论可知,在同圆中,圆的两条平行弦所夹的弧相等,以后若遇到圆的两条平行弦,可考虑运用它们所夹的弧相等证明两条弧所对的弦、圆心角分别相等.
知识点
弧、弦、圆心角之间关系的推论
知3-讲
3
1. 推论
在同圆或等圆中,如果两个圆心角、两条弧和两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.
2. 弦和弦心距(圆心到弦的距离)之间的关系(拓展)
在同圆或等圆中,如果两条弦的弦心距相等,那么这两条弦相等.注意:涉及弦心距的问题,应用时要加上垂直的条件.
知3-讲
拓宽视野:
在同圆或等圆中,两个圆心角、两条弦、两条弧、两个弦心距中如果有一组量相等,那么它们所对应的其余各组量也分别相等.
知3-讲
如图2.2-6, 在⊙O中, AB=CD, 则在① AB=CD;②AC=BD;③∠AOC= ∠BOD;④AC =BD中,正确的个数是( )
A. 1 B. 2
C. 3 D. 4
D
例 3
解题秘方:紧扣弧、弦、圆心角之间关系的推论判断.
︵
︵
︵
︵
知3-讲
解:∵AB = CD,
∴ AB=CD,故①正确.
∵AB = CD,∴AC = BD .
∴ AC=BD,∠ AOC= ∠ BOD,故②③④正确.
︵
︵
︵
︵
︵
︵
知3-讲
解法提醒:
在同一个圆中, 弧、弦和圆心角中只要有一组量相等,就能推出另两组量相等. 线段有和差,弧也有和差.
圆心角
圆心角
弦心距
弧
弦
2.2 圆心角、圆周角
第2章 圆
2.2.1 圆心角
知识点
圆的旋转不变性、圆心角
知1-讲
1
1. 圆的旋转不变性
圆是中心对称图形,圆心就是它的对称中心. 圆具有旋转不变性,把圆绕圆心旋转任意一个角度,所得的图形都与原图形重合.
知1-讲
2. 圆心角
顶点在圆心,角的两边与圆相交,像这样的角叫作圆心角,如图2.2-1,∠AOB是AB所对的圆心角,AB是∠AOB所对的弧. 注意一条弧所对的圆心角只有一个.
︵
︵
知1-讲
特别提醒:
圆心角的条件:
1. 顶点在圆心;
2. 两条边和圆相交.
其中“顶点在圆心”是圆心角的必备条件.
知1-讲
例 1
如图2.2-2,已知A,B是⊙ O上的两点,
∠ AOB=120°,则OA ∶ AB 的值为( )
C
技巧提醒:
特殊的圆心角所对的弦与半径之间的特殊关系:
1. 60°的圆心角所对的弦等于半径;
2.90°的圆心角所对的弦等于半径的 倍;
3. 120°的圆心角所对的弦等于半径的 倍.
知1-讲
解题秘方:紧扣圆心角的定义,将圆心角转化为等腰三角形的顶角,利用等腰三角形的性质探究半径与弦之间的关系.
知1-讲
解:如图2.2-2,过点O作ON⊥ AB于点N.
∵ OA=OB,∴ AN= AB.
∵∠AOB=120°,OA=OB,∴∠ A=30° .
设ON=a,则OA=2a,
∵ OA2-ON2=AN2,
∴ AN= a. ∴ AB=2 a.
∴ OA ∶ AB=2a ∶2 a= .
知2-讲
知识点
弧、弦、圆心角之间的关系
2
1. 关系
在同圆或等圆中,如果圆心角相等,那么它们所对的弧相等,所对的弦也相等.
警示误区:
不能忽略在同圆或等圆中这个前提,如果丢掉了这个前提,即使圆心角相等,所对的弧、弦也不一定相等.如图2.2-4,两个圆的圆心相同,AB与A′B′对应的圆心角相等,但AB≠A′B′,AB ≠A′B′.
︵
︵
︵
︵
知2-讲
2. 示例:弧、弦、圆心角的关系
如图2.2-3,若∠ AOB= ∠ A′OB′,则AB = A′B′,AB=A′B′
︵
︵
知2-讲
如图2.2-5,AB,CD 是⊙ O 的两条直径,弦CE ∥ AB,求证:BC = AE .
解题秘方:构造圆心角,利用“在同圆中,相等的圆心角所对的弧相等”证明.
例2
︵
︵
知2-讲
证明:如图2.2-5,连接OE.
∵ OE=OC,∴∠C= ∠E.
∵ CE∥AB,
∴∠C=∠BOC,∠E=∠AOE.
∴∠BOC=∠AOE.
∴BC = AE .
︵
︵
知2-讲
技巧提醒:
由例2的结论可知,在同圆中,圆的两条平行弦所夹的弧相等,以后若遇到圆的两条平行弦,可考虑运用它们所夹的弧相等证明两条弧所对的弦、圆心角分别相等.
知识点
弧、弦、圆心角之间关系的推论
知3-讲
3
1. 推论
在同圆或等圆中,如果两个圆心角、两条弧和两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.
2. 弦和弦心距(圆心到弦的距离)之间的关系(拓展)
在同圆或等圆中,如果两条弦的弦心距相等,那么这两条弦相等.注意:涉及弦心距的问题,应用时要加上垂直的条件.
知3-讲
拓宽视野:
在同圆或等圆中,两个圆心角、两条弦、两条弧、两个弦心距中如果有一组量相等,那么它们所对应的其余各组量也分别相等.
知3-讲
如图2.2-6, 在⊙O中, AB=CD, 则在① AB=CD;②AC=BD;③∠AOC= ∠BOD;④AC =BD中,正确的个数是( )
A. 1 B. 2
C. 3 D. 4
D
例 3
解题秘方:紧扣弧、弦、圆心角之间关系的推论判断.
︵
︵
︵
︵
知3-讲
解:∵AB = CD,
∴ AB=CD,故①正确.
∵AB = CD,∴AC = BD .
∴ AC=BD,∠ AOC= ∠ BOD,故②③④正确.
︵
︵
︵
︵
︵
︵
知3-讲
解法提醒:
在同一个圆中, 弧、弦和圆心角中只要有一组量相等,就能推出另两组量相等. 线段有和差,弧也有和差.
圆心角
圆心角
弦心距
弧
弦
