湘教版九年级下册2.2.2圆周角 课件(共25张PPT)
文档属性
| 名称 | 湘教版九年级下册2.2.2圆周角 课件(共25张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-03 18:07:12 | ||
图片预览







文档简介
(共25张PPT)
2.2 圆心角、圆周角
第2章 圆
2.2.2 圆周角
知识点
圆周角
知1-讲
1
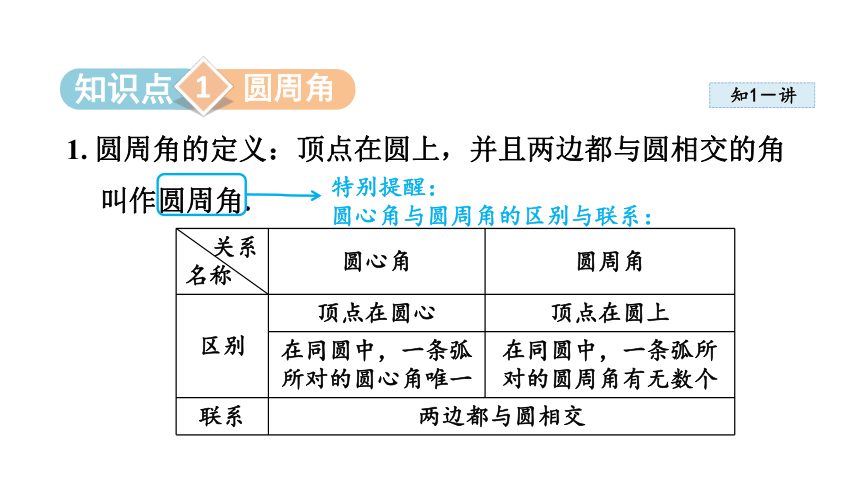
1. 圆周角的定义:顶点在圆上,并且两边都与圆相交的角叫作圆周角.
特别提醒:
圆心角与圆周角的区别与联系:
关系
名称 圆心角 圆周角
区别 顶点在圆心 顶点在圆上
在同圆中,一条弧所对的圆心角唯一 在同圆中,一条弧所对的圆周角有无数个
联系 两边都与圆相交
知1-讲
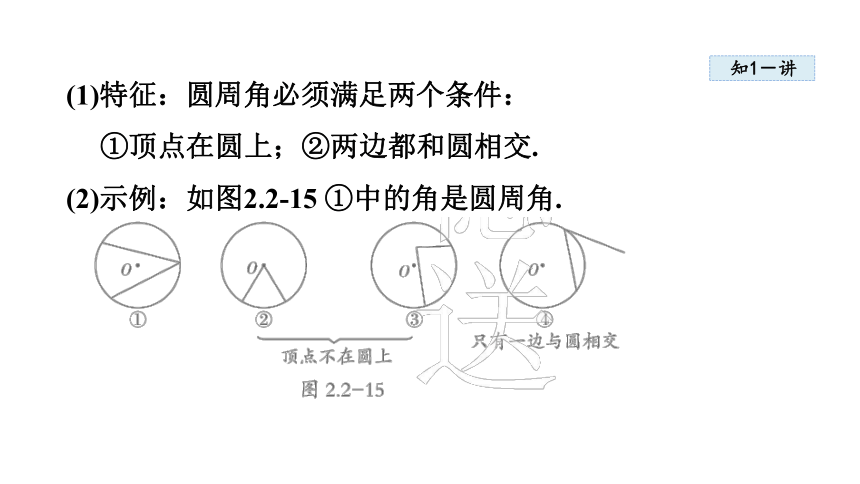
(1)特征:圆周角必须满足两个条件:
①顶点在圆上;②两边都和圆相交.
(2)示例:如图2.2-15 ①中的角是圆周角.
知1-讲
2. 圆周角定理:圆周角的度数等于它所对弧上的圆心角度数的一半.
如图2.2-16,∠ACB= ∠AOB.
特别警示:定理中的圆周角与圆心角是通过它们所对的同一条弧联系在一起的,故不能把同一条弧这个前提省略.
知1-讲
例 1
如图2.2-17,点A,B,C,D 在⊙ O 上,OA⊥BC,垂足为E.若∠ADC=30°,AE=1,则BC=( )
2
B. 4
C.
D.2
A
知1-讲
解题秘方:连接OC,根据圆周角定理求得∠AOC=60°,在Rt △ COE 中可得OE= OC= OA,可得OC的长度,故CE 长度可求得,即可求解.
知1-讲
解:连接OC. ∵∠ ADC=30°,∴∠ AOC=60°.
在Rt△COE 中, =cos 60°= ,
∴ OE= OC= OA. ∴ AE= OA.
∵ AE=1, ∴ OA=OC=2, ∴ CE= .
∵OA⊥BC,垂足为E, ∴易得BC=2 , 故选D.
知1-讲
技巧提醒:
圆周角定理是将圆心角与圆周角进行转化,因此求一个圆周角的度数时,我们可以求与之相等的另一个圆周角的度数,也可以求同弧所对圆心角的度数,可根据题目所给的条件选用其一进行求解.
知2-讲
知识点
圆周角定理的推论
2
1. 推论1:在同圆(或等圆)中,同弧或等弧所对的圆周角相等;相等的圆周角所对的弧也相等.
2. 推论2:(1)直径所对的圆周角是直角;
(2)90°的圆周角所对的弦是直径.
3.“五量关系”定理
在同圆或等圆中,如果两个圆心角、两条弧、两条弧所对的圆周角、两条弦、两条弦的弦心距中有一组量相等,那么它们所对应的其余各组量都分别相等.
知2-讲
2. 点与圆的位置关系
设⊙ O 的半径为r,点P 到圆心的距离OP=d,则有:
点和圆的位置关系 特点 等价关系
点在圆外 点到圆心的距离大于半径 点P在圆外d>r
点在圆上 点到圆心的距离等于半径 点P在圆上d=r
点在圆内 点到圆心的距离小于半径 点P在圆内d<r
知2-讲
特别提醒:
“同弧或等弧”若改为“同弦或等弦”结论就不成立了.因为一条弦所对的圆周角有两种情况:优弧上的圆周角和劣弧上的圆周角.
知2-讲
如图2.2-18,A,B,C,D 是圆上的四个点,∠ABD= ∠ DBC.求证:△ ACD 是等腰三角形.
解题秘方:紧扣“同弧所对的圆周角相等”证明.
例2
方法点拨:
等腰三角形的判定方法:
方法1:有两个角相等的三角形.
方法2:有两条边相等的三角形.
知2-讲
证明:∵ A,B,C,D 是圆上的四个点,
∴∠ACD= ∠ABD,∠DBC= ∠CAD.
又∵∠ABD= ∠DBC,∴∠ACD= ∠CAD.
∴△ACD是等腰三角形.
知2-讲
如图2.2-19,AB是⊙ O 的直径,BD 是⊙ O 的弦,延长BD到点C,使AC=AB. 求证:BD=CD.
解题秘方:紧扣“直径所对的圆周角是直角”结合等腰三角形“三线合一”的性质求证.
例 3
知2-讲
解法提醒:
题中条件有直径,因此可作辅助线,构造直径所对的圆周角(直角)是常用的作辅助线的方法,而题中有条件AB=AC,因此可根据等腰三角形“三线合一”的性质证明BD=CD.
知2-讲
证明:如图2.2-19,连接AD. ∵ AB 是⊙ O 的直径,
∴∠ ADB=90°,即AD ⊥ BC.
又∵ AC=AB,∴ BD=CD.
知2-讲
如图2.2-20,已知经过原点的⊙ P 与x 轴,y 轴分别交于A,B 两点,点C 是弧AB 上一点,则∠ ACB 的度数是( )
A. 80° B. 90°
C. 100° D. 无法确定
解题秘方:利用“90°的圆周角所对的弦是直径”结合“直径所对的圆周角是直角”求解.
例4
B
知2-讲
连接AB,如图2.2-20.
∵∠ AOB=90°,∴ AB 是⊙ P 的直径.
∴∠ ACB=90°.
知2-讲
通用技巧:
常见的作辅助线的方法:
1. 有直径,通常作直径所对的圆周角,从而得出两直线互相垂直,简记为见直径作直角 .
2. 有90°的圆周角,通常作直径,简记为有直角作直径.
知识点
圆内接四边形
知3-讲
3
1. 圆内接四边形
如果一个四边形的四个顶点都在同一个圆上,这个四边形叫作圆内接四边形,这个圆叫作这个四边形的外接圆.
2. 圆内接四边形的性质
圆内接四边形的对角互补.
推论:圆内接四边形的一个外角等于它的内对角.
知3-讲
特别解读:
●内接和外接是一个相对的概念,是一种位置关系.
●每一个圆都有无数个内接四边形,但并不是所有的四边形都有外接圆,只有对角互补的四边形才有外接圆.
知3-讲
[中考·常德]如图2.2-21,四边形ABCD为⊙ O的内接四边形,已知∠BOD=100°,则∠BCD的度数为( )
50°
B. 80°
C. 100°
D. 130°
D
例 5
知3-讲
解题秘方:将所求的角的度数转化为求其所在的圆内接四边形的对角的度数.
特别提醒:
1. 求圆中的某一个圆周角时,根据“圆内接四边形的对角互补”,可以转化为求其所在的圆内接四边形的对角的度数.
2. 圆内接四边形的一组对角其实是圆中一条弦所对的两个圆周角,因此,在同圆或等圆中,相等的弦所对的圆周角相等或互补.
知3-讲
解:∵∠BAD与∠BOD是同弧所对的圆周角和圆心角,∴∠BAD = ∠BOD = ×100°= 50°.
又∵四边形ABCD 为⊙ O 的内接四边形,
∴∠BCD+ ∠BAD = 180°.
∴∠BCD = 180°-∠BAD = 180°-50°= 130°.
圆周角
圆周角
定义
定义
直径所对的圆周角
圆内接四边形的性质
2.2 圆心角、圆周角
第2章 圆
2.2.2 圆周角
知识点
圆周角
知1-讲
1
1. 圆周角的定义:顶点在圆上,并且两边都与圆相交的角叫作圆周角.
特别提醒:
圆心角与圆周角的区别与联系:
关系
名称 圆心角 圆周角
区别 顶点在圆心 顶点在圆上
在同圆中,一条弧所对的圆心角唯一 在同圆中,一条弧所对的圆周角有无数个
联系 两边都与圆相交
知1-讲
(1)特征:圆周角必须满足两个条件:
①顶点在圆上;②两边都和圆相交.
(2)示例:如图2.2-15 ①中的角是圆周角.
知1-讲
2. 圆周角定理:圆周角的度数等于它所对弧上的圆心角度数的一半.
如图2.2-16,∠ACB= ∠AOB.
特别警示:定理中的圆周角与圆心角是通过它们所对的同一条弧联系在一起的,故不能把同一条弧这个前提省略.
知1-讲
例 1
如图2.2-17,点A,B,C,D 在⊙ O 上,OA⊥BC,垂足为E.若∠ADC=30°,AE=1,则BC=( )
2
B. 4
C.
D.2
A
知1-讲
解题秘方:连接OC,根据圆周角定理求得∠AOC=60°,在Rt △ COE 中可得OE= OC= OA,可得OC的长度,故CE 长度可求得,即可求解.
知1-讲
解:连接OC. ∵∠ ADC=30°,∴∠ AOC=60°.
在Rt△COE 中, =cos 60°= ,
∴ OE= OC= OA. ∴ AE= OA.
∵ AE=1, ∴ OA=OC=2, ∴ CE= .
∵OA⊥BC,垂足为E, ∴易得BC=2 , 故选D.
知1-讲
技巧提醒:
圆周角定理是将圆心角与圆周角进行转化,因此求一个圆周角的度数时,我们可以求与之相等的另一个圆周角的度数,也可以求同弧所对圆心角的度数,可根据题目所给的条件选用其一进行求解.
知2-讲
知识点
圆周角定理的推论
2
1. 推论1:在同圆(或等圆)中,同弧或等弧所对的圆周角相等;相等的圆周角所对的弧也相等.
2. 推论2:(1)直径所对的圆周角是直角;
(2)90°的圆周角所对的弦是直径.
3.“五量关系”定理
在同圆或等圆中,如果两个圆心角、两条弧、两条弧所对的圆周角、两条弦、两条弦的弦心距中有一组量相等,那么它们所对应的其余各组量都分别相等.
知2-讲
2. 点与圆的位置关系
设⊙ O 的半径为r,点P 到圆心的距离OP=d,则有:
点和圆的位置关系 特点 等价关系
点在圆外 点到圆心的距离大于半径 点P在圆外d>r
点在圆上 点到圆心的距离等于半径 点P在圆上d=r
点在圆内 点到圆心的距离小于半径 点P在圆内d<r
知2-讲
特别提醒:
“同弧或等弧”若改为“同弦或等弦”结论就不成立了.因为一条弦所对的圆周角有两种情况:优弧上的圆周角和劣弧上的圆周角.
知2-讲
如图2.2-18,A,B,C,D 是圆上的四个点,∠ABD= ∠ DBC.求证:△ ACD 是等腰三角形.
解题秘方:紧扣“同弧所对的圆周角相等”证明.
例2
方法点拨:
等腰三角形的判定方法:
方法1:有两个角相等的三角形.
方法2:有两条边相等的三角形.
知2-讲
证明:∵ A,B,C,D 是圆上的四个点,
∴∠ACD= ∠ABD,∠DBC= ∠CAD.
又∵∠ABD= ∠DBC,∴∠ACD= ∠CAD.
∴△ACD是等腰三角形.
知2-讲
如图2.2-19,AB是⊙ O 的直径,BD 是⊙ O 的弦,延长BD到点C,使AC=AB. 求证:BD=CD.
解题秘方:紧扣“直径所对的圆周角是直角”结合等腰三角形“三线合一”的性质求证.
例 3
知2-讲
解法提醒:
题中条件有直径,因此可作辅助线,构造直径所对的圆周角(直角)是常用的作辅助线的方法,而题中有条件AB=AC,因此可根据等腰三角形“三线合一”的性质证明BD=CD.
知2-讲
证明:如图2.2-19,连接AD. ∵ AB 是⊙ O 的直径,
∴∠ ADB=90°,即AD ⊥ BC.
又∵ AC=AB,∴ BD=CD.
知2-讲
如图2.2-20,已知经过原点的⊙ P 与x 轴,y 轴分别交于A,B 两点,点C 是弧AB 上一点,则∠ ACB 的度数是( )
A. 80° B. 90°
C. 100° D. 无法确定
解题秘方:利用“90°的圆周角所对的弦是直径”结合“直径所对的圆周角是直角”求解.
例4
B
知2-讲
连接AB,如图2.2-20.
∵∠ AOB=90°,∴ AB 是⊙ P 的直径.
∴∠ ACB=90°.
知2-讲
通用技巧:
常见的作辅助线的方法:
1. 有直径,通常作直径所对的圆周角,从而得出两直线互相垂直,简记为见直径作直角 .
2. 有90°的圆周角,通常作直径,简记为有直角作直径.
知识点
圆内接四边形
知3-讲
3
1. 圆内接四边形
如果一个四边形的四个顶点都在同一个圆上,这个四边形叫作圆内接四边形,这个圆叫作这个四边形的外接圆.
2. 圆内接四边形的性质
圆内接四边形的对角互补.
推论:圆内接四边形的一个外角等于它的内对角.
知3-讲
特别解读:
●内接和外接是一个相对的概念,是一种位置关系.
●每一个圆都有无数个内接四边形,但并不是所有的四边形都有外接圆,只有对角互补的四边形才有外接圆.
知3-讲
[中考·常德]如图2.2-21,四边形ABCD为⊙ O的内接四边形,已知∠BOD=100°,则∠BCD的度数为( )
50°
B. 80°
C. 100°
D. 130°
D
例 5
知3-讲
解题秘方:将所求的角的度数转化为求其所在的圆内接四边形的对角的度数.
特别提醒:
1. 求圆中的某一个圆周角时,根据“圆内接四边形的对角互补”,可以转化为求其所在的圆内接四边形的对角的度数.
2. 圆内接四边形的一组对角其实是圆中一条弦所对的两个圆周角,因此,在同圆或等圆中,相等的弦所对的圆周角相等或互补.
知3-讲
解:∵∠BAD与∠BOD是同弧所对的圆周角和圆心角,∴∠BAD = ∠BOD = ×100°= 50°.
又∵四边形ABCD 为⊙ O 的内接四边形,
∴∠BCD+ ∠BAD = 180°.
∴∠BCD = 180°-∠BAD = 180°-50°= 130°.
圆周角
圆周角
定义
定义
直径所对的圆周角
圆内接四边形的性质
