湘教版九年级下册 2.3垂径定理 (共22张)
文档属性
| 名称 | 湘教版九年级下册 2.3垂径定理 (共22张) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-03 19:00:09 | ||
图片预览







文档简介
(共22张PPT)
*2.3 垂径定理
第2章 圆
知识点
垂径定理
知1-讲
1
1. 垂径定理
垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.
特别提醒:
1. “垂直于弦的直径”中的“直径”,还可以是垂直于弦的半径或过圆心垂直于弦的直线.其实质是:过圆心且垂直于弦的线段、直线均可.
2“. 两条弧”是指弦所对的劣弧和优弧或两个半圆.
知1-讲
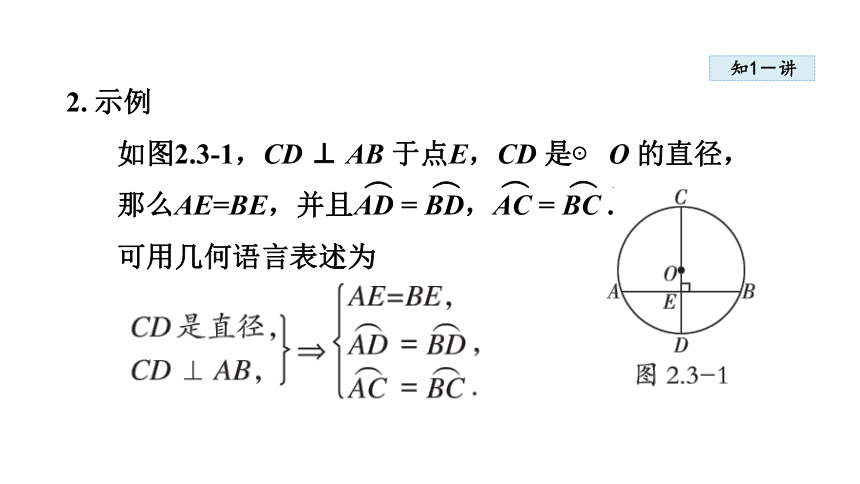
2. 示例
如图2.3-1,CD ⊥ AB 于点E,CD 是⊙ O 的直径,
那么AE=BE,并且AD = BD,AC = BC .
可用几何语言表述为
︵
︵
︵
︵
知1-讲
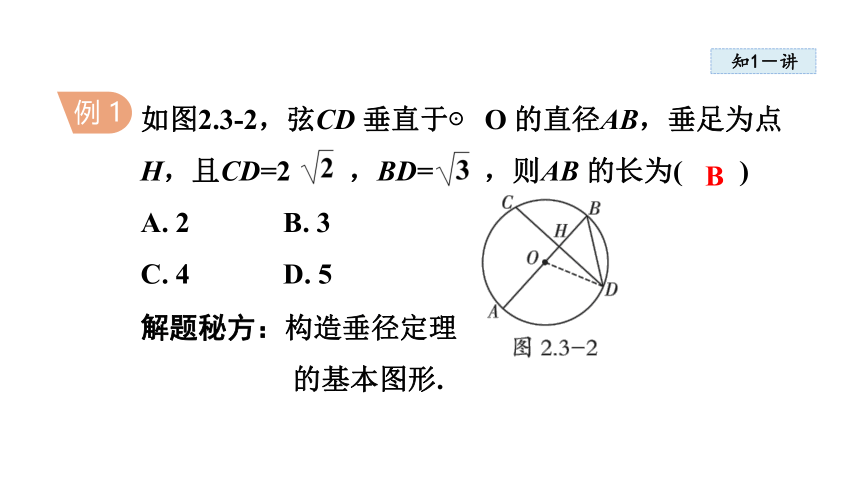
例 1
如图2.3-2,弦CD 垂直于⊙ O 的直径AB,垂足为点H,且CD=2 ,BD= ,则AB 的长为( )
A. 2 B. 3
C. 4 D. 5
B
解题秘方:构造垂径定理的基本图形.
知1-讲
方法提醒:
利用垂径定理求线段的长的方法:
求线段长时,一般把半径、圆心到弦的垂线段、弦的一半构建在一个直角三角形里,运用勾股定理求解,即用“垂径定理+勾股定理”求解.
知1-讲
解:连接OD,如图2.3-2.
∵ CD⊥AB,CD=2 ,
∴ CH=DH= .
在Rt△BHD中,由勾股定理,得BH=1.
设⊙ O的半径为r, 在Rt△OHD 中,OH2+HD2=OD2, 即(r-1)2+( )2=r2.
解得r= .∴ AB=3.
知1-讲
如图2.3-3,在⊙ O中,AB 为⊙ O 的弦,C,D 是直线AB上两点,且AC=BD.
求证:△ OCD 为等腰三角形.
例2
解题秘方:构建垂径定理的基本图形结合线段垂直平分线性质证明.
知1-讲
解题通法:
证明线段相等、证明垂直、证明角相等都经常用到垂径定理.在使用时,若已知圆心,作垂直于弦的半径(或直径)或连半径,是常用的作辅助线的方法.
知1-讲
证明:过点O 作OM ⊥ AB,垂足为M,
如图2.3-3.
∵ OM ⊥ AB,∴ AM=BM.
∵ AC=BD,∴ CM=DM.
又∵ OM ⊥ CD,∴ OC=OD.
∴△ OCD 为等腰三角形.
知2-讲
知识点
点与圆的位置关系
2
1. 推论:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
知2-讲
2. 示例:如图2.3-4,CD 是⊙ O 的直径,AB 是弦(非直径),AB 与CD 相交于点E,且AE=BE,那么CD 垂直于AB,并且AD = BD,AC = BC .可用几何语言表述为
︵
︵
︵
︵
知2-讲
拓宽视野:
对于圆中的一条直线,如果具备下列五个条件中的任意两个,那么一定具备其他三个:(1)过圆心;(2)垂直于弦;(3)平分弦(非直径);(4)平分弦所对的劣弧;(5)平分弦所对的优弧.
简记为“知二推三”.
知2-讲
如图2.3-5,AB,CD 是⊙ O 的弦,M,N 分别为AB,CD 的中点,且∠ AMN = ∠ CNM. 求证:AB=CD.
例 3
知2-讲
解题秘方:根据弦的中点作符合垂径定理推论的基本图形,再结合全等三角形的判定和性质进行证明.
解题通法:
证明两条弦相等的方法:
证明两条弦相等,可以先证明弦的一半相等.根据垂径定理的推论,连接圆心和弦的中点是常见的作辅助线的方法.
知2-讲
证明:如图2.3-5,连接OM,ON,OA,OC.
∵ O 为圆心,且M,N 分别为AB,CD 的中点,
∴ AB=2AM,CD=2CN,OM ⊥ AB,ON ⊥ CD.
∴∠OMA= ∠ONC=90° .
∵∠AMN= ∠CNM,
∴∠OMN= ∠ONM.∴ OM=ON.
又∵ OA=OC,∴ Rt △ OAM ≌ Rt △ OCN(HL).
∴ AM=CN. ∴ AB=CD.
知3-讲
如图2.3-6,要把残破的圆片修复完整. 已知弧上的三点A,B,C,用尺规作图找出ABC所在圆的圆心(保留作图痕迹).
例4
︵
知3-讲
解题秘方:紧扣垂径定理的推论,利用垂直平分弦的直线经过圆心来找圆心.
方法点拨:
在垂径定理的推论“知二推三”中,若已知“垂直平分弦”则可推出“经过圆心,平分弦所对的两条弧”,故两条不平行且不重合的弦的垂直平分线的交点即为圆心.
知3-讲
解:如图2.3-6,连接AB,BC,分别作AB,BC 的垂直平分线,两条垂直平分线的交点O 即为所求圆的圆心.
知3-讲
如图2.3-7,一条公路的转弯处是一段圆弧(AB ),点O 是这段弧所在圆的圆心,点C 是AB 的中点,半径OC 与AB 相交于点D,AB=120 m,CD=20 m,求这段弯路所在圆的半径.
例 5
︵
︵
知3-讲
解题秘方:紧扣垂径定理的推论,利用“平分弧,且经过圆心”推出“垂直平分弦”,结合勾股定理求出半径的长.
方法点拨:
本题条件中出现弧的中点,根据垂径定理的推论可知连接圆心和弧的中点的线垂直平分该弧所对的弦.
知3-讲
解:连接OB,如图2.3-7.
∵点C 是AB的中点,∴ OC ⊥ AB,AD=BD=
AB=60 m.
设OB=OC=r m,在Rt △ OBD 中,OB2=OD2+BD2,
∴ r2=(r-20)2+602.
∴ r=100,即这段弯路所在圆的半径为100 m.
︵
垂径定理
垂径定理
平分弧
垂径定理的推论
平分弦所对的弧
垂直于弦
*2.3 垂径定理
第2章 圆
知识点
垂径定理
知1-讲
1
1. 垂径定理
垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.
特别提醒:
1. “垂直于弦的直径”中的“直径”,还可以是垂直于弦的半径或过圆心垂直于弦的直线.其实质是:过圆心且垂直于弦的线段、直线均可.
2“. 两条弧”是指弦所对的劣弧和优弧或两个半圆.
知1-讲
2. 示例
如图2.3-1,CD ⊥ AB 于点E,CD 是⊙ O 的直径,
那么AE=BE,并且AD = BD,AC = BC .
可用几何语言表述为
︵
︵
︵
︵
知1-讲
例 1
如图2.3-2,弦CD 垂直于⊙ O 的直径AB,垂足为点H,且CD=2 ,BD= ,则AB 的长为( )
A. 2 B. 3
C. 4 D. 5
B
解题秘方:构造垂径定理的基本图形.
知1-讲
方法提醒:
利用垂径定理求线段的长的方法:
求线段长时,一般把半径、圆心到弦的垂线段、弦的一半构建在一个直角三角形里,运用勾股定理求解,即用“垂径定理+勾股定理”求解.
知1-讲
解:连接OD,如图2.3-2.
∵ CD⊥AB,CD=2 ,
∴ CH=DH= .
在Rt△BHD中,由勾股定理,得BH=1.
设⊙ O的半径为r, 在Rt△OHD 中,OH2+HD2=OD2, 即(r-1)2+( )2=r2.
解得r= .∴ AB=3.
知1-讲
如图2.3-3,在⊙ O中,AB 为⊙ O 的弦,C,D 是直线AB上两点,且AC=BD.
求证:△ OCD 为等腰三角形.
例2
解题秘方:构建垂径定理的基本图形结合线段垂直平分线性质证明.
知1-讲
解题通法:
证明线段相等、证明垂直、证明角相等都经常用到垂径定理.在使用时,若已知圆心,作垂直于弦的半径(或直径)或连半径,是常用的作辅助线的方法.
知1-讲
证明:过点O 作OM ⊥ AB,垂足为M,
如图2.3-3.
∵ OM ⊥ AB,∴ AM=BM.
∵ AC=BD,∴ CM=DM.
又∵ OM ⊥ CD,∴ OC=OD.
∴△ OCD 为等腰三角形.
知2-讲
知识点
点与圆的位置关系
2
1. 推论:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
知2-讲
2. 示例:如图2.3-4,CD 是⊙ O 的直径,AB 是弦(非直径),AB 与CD 相交于点E,且AE=BE,那么CD 垂直于AB,并且AD = BD,AC = BC .可用几何语言表述为
︵
︵
︵
︵
知2-讲
拓宽视野:
对于圆中的一条直线,如果具备下列五个条件中的任意两个,那么一定具备其他三个:(1)过圆心;(2)垂直于弦;(3)平分弦(非直径);(4)平分弦所对的劣弧;(5)平分弦所对的优弧.
简记为“知二推三”.
知2-讲
如图2.3-5,AB,CD 是⊙ O 的弦,M,N 分别为AB,CD 的中点,且∠ AMN = ∠ CNM. 求证:AB=CD.
例 3
知2-讲
解题秘方:根据弦的中点作符合垂径定理推论的基本图形,再结合全等三角形的判定和性质进行证明.
解题通法:
证明两条弦相等的方法:
证明两条弦相等,可以先证明弦的一半相等.根据垂径定理的推论,连接圆心和弦的中点是常见的作辅助线的方法.
知2-讲
证明:如图2.3-5,连接OM,ON,OA,OC.
∵ O 为圆心,且M,N 分别为AB,CD 的中点,
∴ AB=2AM,CD=2CN,OM ⊥ AB,ON ⊥ CD.
∴∠OMA= ∠ONC=90° .
∵∠AMN= ∠CNM,
∴∠OMN= ∠ONM.∴ OM=ON.
又∵ OA=OC,∴ Rt △ OAM ≌ Rt △ OCN(HL).
∴ AM=CN. ∴ AB=CD.
知3-讲
如图2.3-6,要把残破的圆片修复完整. 已知弧上的三点A,B,C,用尺规作图找出ABC所在圆的圆心(保留作图痕迹).
例4
︵
知3-讲
解题秘方:紧扣垂径定理的推论,利用垂直平分弦的直线经过圆心来找圆心.
方法点拨:
在垂径定理的推论“知二推三”中,若已知“垂直平分弦”则可推出“经过圆心,平分弦所对的两条弧”,故两条不平行且不重合的弦的垂直平分线的交点即为圆心.
知3-讲
解:如图2.3-6,连接AB,BC,分别作AB,BC 的垂直平分线,两条垂直平分线的交点O 即为所求圆的圆心.
知3-讲
如图2.3-7,一条公路的转弯处是一段圆弧(AB ),点O 是这段弧所在圆的圆心,点C 是AB 的中点,半径OC 与AB 相交于点D,AB=120 m,CD=20 m,求这段弯路所在圆的半径.
例 5
︵
︵
知3-讲
解题秘方:紧扣垂径定理的推论,利用“平分弧,且经过圆心”推出“垂直平分弦”,结合勾股定理求出半径的长.
方法点拨:
本题条件中出现弧的中点,根据垂径定理的推论可知连接圆心和弧的中点的线垂直平分该弧所对的弦.
知3-讲
解:连接OB,如图2.3-7.
∵点C 是AB的中点,∴ OC ⊥ AB,AD=BD=
AB=60 m.
设OB=OC=r m,在Rt △ OBD 中,OB2=OD2+BD2,
∴ r2=(r-20)2+602.
∴ r=100,即这段弯路所在圆的半径为100 m.
︵
垂径定理
垂径定理
平分弧
垂径定理的推论
平分弦所对的弧
垂直于弦
