湘教版九年级下册 2.5直线与圆的位置关系 (共61张)
文档属性
| 名称 | 湘教版九年级下册 2.5直线与圆的位置关系 (共61张) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-03 19:09:19 | ||
图片预览










文档简介
(共61张PPT)
2.5 直线与圆的位置关系
第2章 圆
知识点
直线与圆的位置关系
知1-讲
1
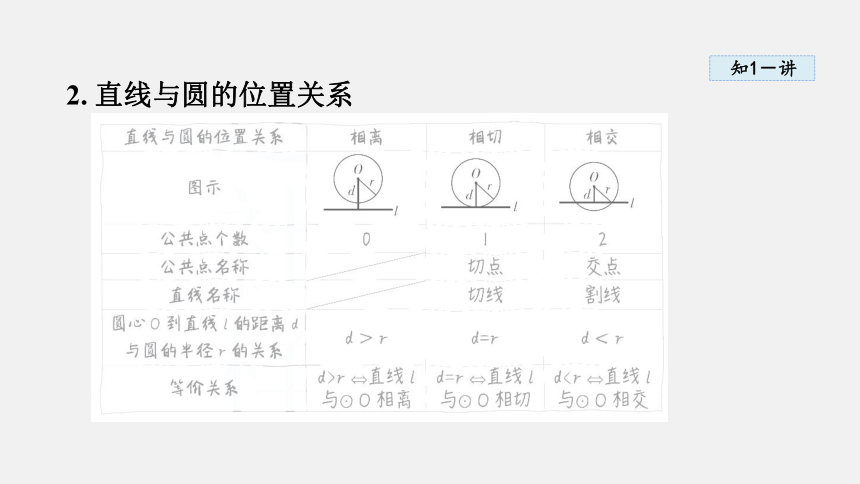
1. 设圆心到直线的距离为d,圆的半径为r,则:
当d当d=r 时,直线与圆只有一个公共点,这时称直线与圆相切,这条直线叫作圆的切线,这个公共点叫作切点;
当d>r 时,直线与圆没有公共点,这时称直线与圆相离.
知1-讲
2. 直线与圆的位置关系
知1-讲
要点提醒:
1. 如果一条直线满足下列三个条件中的任意两个,那么第三个也成立:
(1)过圆心;
(2)过切点;
(3)垂直于切线.
2. 根据切线的定义,可以知道切线具备的性质有:
(1)切线和圆只有一个公共点;
(2)切点到圆心的距离等于半径.
知1-讲
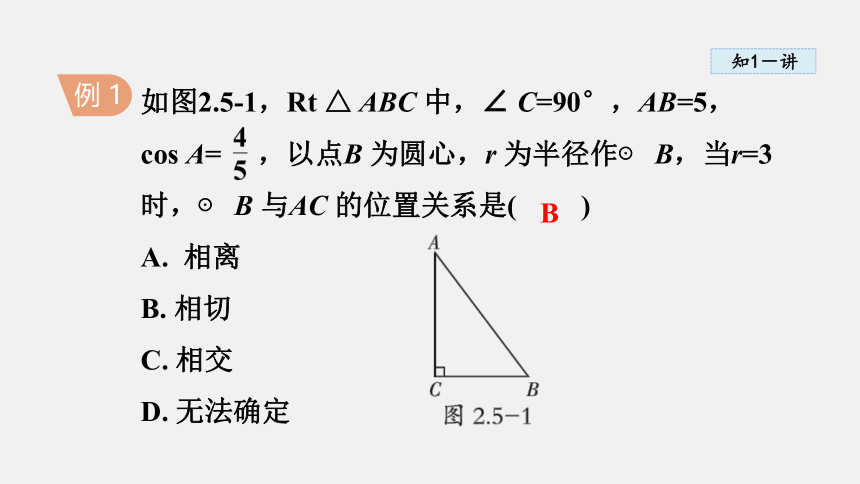
例 1
如图2.5-1,Rt △ ABC 中,∠ C=90°,AB=5,
cos A= ,以点B 为圆心,r 为半径作⊙ B,当r=3 时,⊙ B 与AC 的位置关系是( )
相离
B. 相切
C. 相交
D. 无法确定
B
知1-讲
解法提醒:
判定直线与圆的位置关系的方法:
1.根据直线与圆的公共点的个数判定;
2.将圆心到直线的距离d与圆的半径r相比较,在没有给出d与r的具体数值的情况下,可先利用图形条件及性质求出d 与r 的值,再通过比较大小判定其位置关系.
知1-讲
解题秘方:根据Rt △ ABC 中,∠ C=90°,cos A= ,求出AC 的值. 再根据勾股定理求出BC 的值,比较BC 与半径r 的大小,即可得出⊙ B 与AC的关系.
知1-讲
解:∵ Rt △ ABC 中,∠ C=90°,cos A= ,
∴ .
∵ AB=5,∴ AC=4. ∴ BC= =3.
又∵ r=3,∴⊙ B 与AC 的位置关系是相切. 故选B.
知1-讲
如图2.5-2,在△ ABC 中,∠ C=90°,∠ A=30°,O 是AB上的一点,OB=m(m>0),⊙ O 的半径r 为 ,当m 分别在什么范围内取值时,直线BC 与⊙ O 相离、相切、相交?
例2
知1-讲
解题秘方:利用直线与圆的位置关系建立方程(或不等式)求m 的范围.
解法提醒:
要判断OB=m 在什么范围内取值时,直线BC与⊙ O 相离、相切、相交,就要求出圆心O到直线BC 的距离d,把d 与⊙ O的半径r的大小进行比较,并利用直线与圆的位置关系中相切、相离、相交时d与r之间的相等或不等关系,将其转化为解方程或不等式的问题,从而求出m 的取值范围.
知1-讲
解:如图2.5-2,作OD ⊥ BC 于点D.
∵∠ A=30°,∠ C=90°,∴∠ B=60° .
∴∠ DOB=30° .
在Rt △ ODB 中,∵ OB=m,
∴ DB= 1m,OD= m.
设OD=d.
(1)当直线BC 与⊙ O 相离时,d > r,即 m > ,解得m > .
知1-讲
(2)当直线BC 与⊙ O 相切时,d=r,
即 m = ,解得m= .
(3)当直线BC 与⊙ O 相交时,d < r,
即 m< ,解得m < .
又∵ m > 0,∴ 0 < m < .
知2-讲
知识点
切线的判定
2
1. 判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线.
2. 判定方法
(1)定义法:与圆有唯一公共点的直线是圆的切线;
(2)数量关系法:圆心到直线的距离等于半径的直线是圆的切线;
(3)判定定理法:经过半径的外端并且垂直于这条半径的直线是圆的切线.
知2-讲
特别提醒:
切线必须同时具备两个条件:
1. 直线过半径的外端;
2. 直线垂直于这条半径.
知2-讲
如图2.5-3,已知AB 是⊙ O 的直径,AB=4,点C 在线段AB 的延长线上,点D 在⊙ O 上,连接CD,且CD=OA,OC=2 ,求证:CD 是⊙ O 的切线.
例 3
解题秘方:利用“有切点,连半径,证垂直”判定圆的切线.
知2-讲
证明:如图2.5-3,连接OD.
由题意可知CD=OD=OA= AB=2.
∵ OC=2 ,∴ OD2+CD2=OC2.
∴∠ ODC=90°,即OD ⊥ CD.
又∵点D 在⊙ O 上,
∴ CD 是⊙ O 的切线.
知2-讲
技巧提醒:
作辅助线判定圆的切线的常用方法:
1. 有切点, 连半径, 证垂直. 如果已知直线经过圆上的一点,那么连接这点和圆心,得到辅助半径,再证明所作半径与这条直线垂直即可,简记为:有切点,连半径,证垂直.
2. 无切点, 作垂线, 证半径. 如果已知条件中不知道直线与圆是否有公共点,那么过圆心作直线的垂线段,再证明垂线段的长度等于半径即可,简记为:无切点,作垂线,证半径.
知2-讲
如图2.5-4,在Rt △ ABC 中,∠ B=90°,∠ BAC 的平分线交BC 于点D,以点D 为圆心,DB 长为半径作⊙ D.求证:AC 与⊙ D 相切.
解题秘方:利用“无切点,作垂线,证半径”判定圆的切线.
例4
知2-讲
证明:如图2.5-4,过点D 作DF ⊥ AC 于点F.
∵∠ B=90°,
∴ DB ⊥ AB.
又∵ AD 平分∠ BAC,
∴ DF=DB.
∴ AC 与⊙ D 相切.
知识点
切线的性质
知3-讲
3
1. 性质定理:圆的切线垂直于过切点的半径.
2. 切线的性质
(1)切线和圆只有一个公共点.
(2)圆心到切线的距离等于半径.
(3)圆的切线垂直于过切点的半径.
(4)经过圆心且垂直于切线的直线必过切点(找切点用).
(5)经过切点且垂直于切线的直线必过圆心(找圆心用).
以上(3)(4)(5)可归纳为,如果直线满足过圆心、过切点、垂直于切线这三个条件中的任意两个,那么第三个也成立.
知3-讲
特别提醒:
1. 性质定理的题设有两个条件:(1)圆的切线;(2)半径过切点.应用时缺一不可.
2. 切线的判定定理与性质定理的区别:切线的判定定理是在未知相切而要证明相切的情况下使用;切线的性质定理是在已知相切而要推得其他的结论时使用.它们是一个互逆的过程,不要混淆.
知3-讲
如图2.5-5,AB 为⊙ O 的直径,PD 切⊙ O 于点C,交AB的延长线于点D,且∠ D=2 ∠ CAD.
例 5
知3-讲
(1)求∠ D 的度数.
解题秘方:利用“等半径”得等腰三角形;
知3-讲
解:如图2.5-5,连接OC. ∵ AO=CO,
∴∠OAC= ∠ACO. ∴∠COD=2 ∠CAD.
又∵∠D=2 ∠CAD,∴∠ D= ∠COD.
∵ PD 切⊙ O 于点C,∴ OC ⊥ PD,
即∠ OCD=90° . ∴∠D=45° .
知3-讲
(2)若CD=2,求BD 的长.
解题秘方:利用“圆的切线垂直于过切点的半径”构造直角三角形,再结合相关性质求解.
解法提醒:
已知圆的切线时,常连接圆心和切点,得到半径垂直于切线,通过构造直角三角形来解决问题,即“见切线,连半径,得垂线”;而等半径,可得等腰三角形,从而可得两底角相等;在同圆中有关切线的问题常通过等腰三角形和直角三角形的性质来解决.
知3-讲
解:由(1)可知△OCD是等腰直角三角形.
∴ OC=CD=2.
由勾股定理,得OD= ,
∴ BD=OD-OB=2 -2.
知3-讲
[中考·湖州]如图2.5-6,已知BC 是⊙ O 的直径,AC 切⊙ O 于点C,AB 交⊙ O 于点D,E 为AC 的中点,连接DE.
例6
知3-讲
(1)若AD=DB,OC=5,求切线AC 的长;
解题秘方:构造直径所对的圆周角,利用直径所对的圆周角是直角求解;
知3-讲
解:连接CD,如图2.5-6.
∵ BC 是⊙ O 的直径,∴∠ BDC=90°,
即CD ⊥ AB.
∵ AD=DB,∴ AC=BC=2OC=10.
知3-讲
(2)求证:DE 是⊙ O 的切线.
解题秘方:利用“连半径,证垂直”求解.
知3-讲
证明:连接OD,如图2.5-6.
易知∠ ADC=90°,∵ E 为AC 的中点,
∴ DE=EC= AC. ∴∠ 1 =∠ 2.
∵ OD=OC,∴∠ 3 =∠ 4.
∵ AC 切⊙ O 于点C,∴ AC ⊥ OC.
∴∠ 1+ ∠ 3= ∠ 2+ ∠ 4 = 90°,即DE ⊥ OD.
∴ DE 是⊙ O 的切线.
知3-讲
解法提醒:
看到切线,就想作过切点的半径;看到直径,就想直径所对的圆周角是直角;看到切线的判定,就想:(1)若已知直线与圆的公共点,则采用判定定理法,其基本思路是:连接过这点的半径,证明这条半径与直线垂直即可,可简述为:有切点,连半径,证垂直;(2)若未知直线与圆有公共点,则采用数量关系法,其基本思路是:过圆心作直线的垂线段,证明垂线段的长等于圆的半径,可简述为:无切点,作垂线,证半径.
知4-讲
知识点
切线长定理
4
1. 切线长定义:经过圆外一点作圆的切线,这点和切点之间的线段的长,叫作这点到圆的切线长.
切线是直线,不可度量;切线长是切线上切点与切点外另一点之间的线段的长,可以度量.
知4-讲
2. 切线长定理
过圆外一点所作的圆的两条切线长相等,圆心和这一点的连线平分两条切线的夹角.
特别提醒:
经过圆上一点作圆的切线,有且只有一条,过切点的半径垂直于这条切线;经过圆外一点作圆的切线,有两条,这点和两个切点所连的两条线段相等.
知4-讲
3. 示例
如图2.5-7 是切线长定理的一个基本图形, 可以直接得到结论:
(1)PO ⊥ AB;(2)AO ⊥ AP,BO ⊥ BP;
(3)AP=BP;(4)∠ 1= ∠ 2= ∠ 3= ∠ 4;
(5)AD=BD;
(6)3= BC 等.
︵
知4-讲
如图2.5-8,PA,PB,DE 分别切⊙ O 于点A,B,C,点D在PA 上,点E 在PB 上.
例 7
知4-讲
图解:
如图2.5-9,利用切线长定理,可将求△ PDE 的周长转化为求PA 与PB 的和.
知4-讲
(1)若PA=10,求△ PDE 的周长;
解题秘方:根据切线长的定义,判断出PA,PB,DA,DC,EC,EB 的长都是切线长,再利用切线长定理,找到相等关系.
知4-讲
解:∵ PA,PB,DE 分别切⊙ O 于点A,B,C,
∴ PA=PB,DA=DC,EC=EB.
∴ PD+DE+PE=PD+DA+EB+PE=PA+PB=10+10=20.
∴△ PDE 的周长为20.
知4-讲
(2)若∠ P=50°,求∠ DOE 的度数.
解题秘方:根据切线长的定义,判断出PA,PB,DA,DC,EC,EB 的长都是切线长,再利用切线长定理,找到相等关系.
知4-讲
解:如图2.5-8,连接OA,OC,OB.
∵ PA,PB,DE 是⊙ O 的切线,
∴ OA ⊥ PA,OB ⊥ PB,OC ⊥ DE.
∴∠ DAO= ∠ EBO=90° . ∴∠ P+ ∠ AOB=180° .
∴∠ AOB=180°- 50° =130° .
易知∠ AOD= ∠ DOC,∠ COE= ∠ BOE,
∴∠ DOE= ∠ AOB= ×130°=65°
知4-讲
详解:
由于点D到OA,OC的距离相等,点E到OB,OC 的距离相等,根据在角的内部,到角两边距离相等的点在角的平分线上,可知点D,E分别在∠ AOC,∠ BOC 的平分线上.
知4-讲
如图2.5-10,PA,PB 是⊙ O 的切线,切点分别为A,B,BC 为⊙ O 的直径,连接AB,AC,OP.
例8
知4-讲
求证:(1)∠ APB = 2 ∠ ABC;
解题秘方:活用切线长定理中角的关系结合相关性质求解.
知4-讲
证明:∵ PA,PB 分别切⊙ O 于点A,B,
∴由切线长定理知∠ BPO= ∠ APO= ∠ APB,PA=PB.
∴ PO ⊥ AB. ∴∠ ABP+ ∠ BPO=90° .
又∵ PB 是⊙ O 的切线,∴ OB ⊥ PB.
∴∠ ABP+ ∠ ABC=90° .
∴∠ ABC= ∠ BPO= ∠ APB,即∠ APB=2 ∠ ABC.
知4-讲
(2) AC ∥ OP.
解题秘方:活用切线长定理中角的关系结合相关性质求解.
知4-讲
证明:∵ BC 是⊙ O 的直径,
∴∠ BAC=90°,即AC ⊥ AB.
由(1)知OP ⊥ AB,∴ AC ∥ OP.
知4-讲
特别提醒:
切线长定理揭示了两个方面的内容,一是切线长相等,揭示线段之间的数量关系;二是圆外一点与圆心的连线平分两条切线的夹角,揭示了角之间的数量关系. 这两个方面的内容为证明线段之间的关系或者角之间的关系提供了大量的条件.
知5-讲
知识点
三角形的内切圆
5
1. 三角形的内切圆:与三角形各边都相切的圆叫作三角形的内切圆,内切圆的圆心叫作三角形的内心,这个三角形叫作圆的外切三角形.
要点解读:
1. “内切“” 外切”是针对位置而言的, “内”是相对于三角形而言, “外”是相对于圆而言.
2. 一个三角形有且只有一个内切圆,而一个圆有无数多个外切三角形.
3. 三角形的内心在三角形的内部.在实际操作中,画出三角形任意两个内角的平分线,找到交点,该交点就是三角形的内心.
知5-讲
2. 三角形的内心:三角形的内心是这个三角形的三条角平分线的交点.三角形内心的性质:三角形的内心到三角形三条边的距离都相等,且等于其内切圆的半径.拓宽视野:如图2.5-11,△ ABC 的周长是l,
内切圆⊙ O 的半径为r.
知5-讲
设BC=a,AC=b,AB=c,则S△ ABC=S△ BOC+
S△ AOC+S△ AOB= ar+ br+ cr= (a+b+c)r=
lr.
故三角形的面积可以用三角形的周长与其内切圆半径之积的一半表示.
知5-讲
a,b,c 分别是Rt △ ABC 的三边BC,AC,AB 的长,其中∠ C=90°,求此三角形内切圆的半径.
例 7
知5-讲
特别提醒:
用直角三角形三边长表示其内切圆半径的两种方法:r= 或r= (其中a,b 为直角边长,r 为圆的半径,c 为斜边长,S 是直角三角形的面积).
知5-讲
解题秘方一:将Rt△ABC内切圆的半径转化到Rt △ABC的边上,然后借助切线长定理进行线段间的转化.
知5-讲
解法一:如图2.5-12,设Rt △ ABC 的内切圆⊙ O 的半径为r,⊙ O 分别切AB,BC,AC 于点D,E,F,连接OD,OE,OF,则四边形OECF为正方形.
∴ CE=CF=r. ∴ AF=AD=b-r,BD=BE=a-r.
∵ AD+BD=AB,即b-r+a-r=c,∴ r=
知5-讲
解法二:如图2.5-13,设Rt △ ABC 的内切圆⊙ O 的半径为r,连接OA,OB,OC.
由S △ ABC=S △ AOB+S △ AOC+S △ BOC,
得 ab= (a+b+c)r.
故r= .
解题秘方二:利用等积法求解
知5-讲
如图2.5-14,在△ ABC 中,∠ A=80°,点O 是△ ABC 的内心,求∠ BOC 的度数.
例10
知5-讲
特别提醒:
如图2.5-15 是数学中一个典型的基本图形.在△ABC中,若点P是△ABC的内心,则∠BPC=90°+
∠A;若点P是△ABC的外心,
则∠ BPC=2 ∠ A.
知5-讲
解题秘方:三角形的内心是三角形三个内角的平分线的交点.
知5-讲
解:∵∠ A=80°,
∴∠ ABC+ ∠ ACB=180°-80°=100°.
∵点O 是△ ABC 的内心,
∴∠ OBC= ∠ ABC,∠ OCB= ∠ ACB.
∴∠ OBC+ ∠ OCB= (∠ ABC+ ∠ ACB)=50°.
∴∠ BOC=180°-50°=130°.
直线与圆的位置关系
2.5 直线与圆的位置关系
第2章 圆
知识点
直线与圆的位置关系
知1-讲
1
1. 设圆心到直线的距离为d,圆的半径为r,则:
当d
当d>r 时,直线与圆没有公共点,这时称直线与圆相离.
知1-讲
2. 直线与圆的位置关系
知1-讲
要点提醒:
1. 如果一条直线满足下列三个条件中的任意两个,那么第三个也成立:
(1)过圆心;
(2)过切点;
(3)垂直于切线.
2. 根据切线的定义,可以知道切线具备的性质有:
(1)切线和圆只有一个公共点;
(2)切点到圆心的距离等于半径.
知1-讲
例 1
如图2.5-1,Rt △ ABC 中,∠ C=90°,AB=5,
cos A= ,以点B 为圆心,r 为半径作⊙ B,当r=3 时,⊙ B 与AC 的位置关系是( )
相离
B. 相切
C. 相交
D. 无法确定
B
知1-讲
解法提醒:
判定直线与圆的位置关系的方法:
1.根据直线与圆的公共点的个数判定;
2.将圆心到直线的距离d与圆的半径r相比较,在没有给出d与r的具体数值的情况下,可先利用图形条件及性质求出d 与r 的值,再通过比较大小判定其位置关系.
知1-讲
解题秘方:根据Rt △ ABC 中,∠ C=90°,cos A= ,求出AC 的值. 再根据勾股定理求出BC 的值,比较BC 与半径r 的大小,即可得出⊙ B 与AC的关系.
知1-讲
解:∵ Rt △ ABC 中,∠ C=90°,cos A= ,
∴ .
∵ AB=5,∴ AC=4. ∴ BC= =3.
又∵ r=3,∴⊙ B 与AC 的位置关系是相切. 故选B.
知1-讲
如图2.5-2,在△ ABC 中,∠ C=90°,∠ A=30°,O 是AB上的一点,OB=m(m>0),⊙ O 的半径r 为 ,当m 分别在什么范围内取值时,直线BC 与⊙ O 相离、相切、相交?
例2
知1-讲
解题秘方:利用直线与圆的位置关系建立方程(或不等式)求m 的范围.
解法提醒:
要判断OB=m 在什么范围内取值时,直线BC与⊙ O 相离、相切、相交,就要求出圆心O到直线BC 的距离d,把d 与⊙ O的半径r的大小进行比较,并利用直线与圆的位置关系中相切、相离、相交时d与r之间的相等或不等关系,将其转化为解方程或不等式的问题,从而求出m 的取值范围.
知1-讲
解:如图2.5-2,作OD ⊥ BC 于点D.
∵∠ A=30°,∠ C=90°,∴∠ B=60° .
∴∠ DOB=30° .
在Rt △ ODB 中,∵ OB=m,
∴ DB= 1m,OD= m.
设OD=d.
(1)当直线BC 与⊙ O 相离时,d > r,即 m > ,解得m > .
知1-讲
(2)当直线BC 与⊙ O 相切时,d=r,
即 m = ,解得m= .
(3)当直线BC 与⊙ O 相交时,d < r,
即 m< ,解得m < .
又∵ m > 0,∴ 0 < m < .
知2-讲
知识点
切线的判定
2
1. 判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线.
2. 判定方法
(1)定义法:与圆有唯一公共点的直线是圆的切线;
(2)数量关系法:圆心到直线的距离等于半径的直线是圆的切线;
(3)判定定理法:经过半径的外端并且垂直于这条半径的直线是圆的切线.
知2-讲
特别提醒:
切线必须同时具备两个条件:
1. 直线过半径的外端;
2. 直线垂直于这条半径.
知2-讲
如图2.5-3,已知AB 是⊙ O 的直径,AB=4,点C 在线段AB 的延长线上,点D 在⊙ O 上,连接CD,且CD=OA,OC=2 ,求证:CD 是⊙ O 的切线.
例 3
解题秘方:利用“有切点,连半径,证垂直”判定圆的切线.
知2-讲
证明:如图2.5-3,连接OD.
由题意可知CD=OD=OA= AB=2.
∵ OC=2 ,∴ OD2+CD2=OC2.
∴∠ ODC=90°,即OD ⊥ CD.
又∵点D 在⊙ O 上,
∴ CD 是⊙ O 的切线.
知2-讲
技巧提醒:
作辅助线判定圆的切线的常用方法:
1. 有切点, 连半径, 证垂直. 如果已知直线经过圆上的一点,那么连接这点和圆心,得到辅助半径,再证明所作半径与这条直线垂直即可,简记为:有切点,连半径,证垂直.
2. 无切点, 作垂线, 证半径. 如果已知条件中不知道直线与圆是否有公共点,那么过圆心作直线的垂线段,再证明垂线段的长度等于半径即可,简记为:无切点,作垂线,证半径.
知2-讲
如图2.5-4,在Rt △ ABC 中,∠ B=90°,∠ BAC 的平分线交BC 于点D,以点D 为圆心,DB 长为半径作⊙ D.求证:AC 与⊙ D 相切.
解题秘方:利用“无切点,作垂线,证半径”判定圆的切线.
例4
知2-讲
证明:如图2.5-4,过点D 作DF ⊥ AC 于点F.
∵∠ B=90°,
∴ DB ⊥ AB.
又∵ AD 平分∠ BAC,
∴ DF=DB.
∴ AC 与⊙ D 相切.
知识点
切线的性质
知3-讲
3
1. 性质定理:圆的切线垂直于过切点的半径.
2. 切线的性质
(1)切线和圆只有一个公共点.
(2)圆心到切线的距离等于半径.
(3)圆的切线垂直于过切点的半径.
(4)经过圆心且垂直于切线的直线必过切点(找切点用).
(5)经过切点且垂直于切线的直线必过圆心(找圆心用).
以上(3)(4)(5)可归纳为,如果直线满足过圆心、过切点、垂直于切线这三个条件中的任意两个,那么第三个也成立.
知3-讲
特别提醒:
1. 性质定理的题设有两个条件:(1)圆的切线;(2)半径过切点.应用时缺一不可.
2. 切线的判定定理与性质定理的区别:切线的判定定理是在未知相切而要证明相切的情况下使用;切线的性质定理是在已知相切而要推得其他的结论时使用.它们是一个互逆的过程,不要混淆.
知3-讲
如图2.5-5,AB 为⊙ O 的直径,PD 切⊙ O 于点C,交AB的延长线于点D,且∠ D=2 ∠ CAD.
例 5
知3-讲
(1)求∠ D 的度数.
解题秘方:利用“等半径”得等腰三角形;
知3-讲
解:如图2.5-5,连接OC. ∵ AO=CO,
∴∠OAC= ∠ACO. ∴∠COD=2 ∠CAD.
又∵∠D=2 ∠CAD,∴∠ D= ∠COD.
∵ PD 切⊙ O 于点C,∴ OC ⊥ PD,
即∠ OCD=90° . ∴∠D=45° .
知3-讲
(2)若CD=2,求BD 的长.
解题秘方:利用“圆的切线垂直于过切点的半径”构造直角三角形,再结合相关性质求解.
解法提醒:
已知圆的切线时,常连接圆心和切点,得到半径垂直于切线,通过构造直角三角形来解决问题,即“见切线,连半径,得垂线”;而等半径,可得等腰三角形,从而可得两底角相等;在同圆中有关切线的问题常通过等腰三角形和直角三角形的性质来解决.
知3-讲
解:由(1)可知△OCD是等腰直角三角形.
∴ OC=CD=2.
由勾股定理,得OD= ,
∴ BD=OD-OB=2 -2.
知3-讲
[中考·湖州]如图2.5-6,已知BC 是⊙ O 的直径,AC 切⊙ O 于点C,AB 交⊙ O 于点D,E 为AC 的中点,连接DE.
例6
知3-讲
(1)若AD=DB,OC=5,求切线AC 的长;
解题秘方:构造直径所对的圆周角,利用直径所对的圆周角是直角求解;
知3-讲
解:连接CD,如图2.5-6.
∵ BC 是⊙ O 的直径,∴∠ BDC=90°,
即CD ⊥ AB.
∵ AD=DB,∴ AC=BC=2OC=10.
知3-讲
(2)求证:DE 是⊙ O 的切线.
解题秘方:利用“连半径,证垂直”求解.
知3-讲
证明:连接OD,如图2.5-6.
易知∠ ADC=90°,∵ E 为AC 的中点,
∴ DE=EC= AC. ∴∠ 1 =∠ 2.
∵ OD=OC,∴∠ 3 =∠ 4.
∵ AC 切⊙ O 于点C,∴ AC ⊥ OC.
∴∠ 1+ ∠ 3= ∠ 2+ ∠ 4 = 90°,即DE ⊥ OD.
∴ DE 是⊙ O 的切线.
知3-讲
解法提醒:
看到切线,就想作过切点的半径;看到直径,就想直径所对的圆周角是直角;看到切线的判定,就想:(1)若已知直线与圆的公共点,则采用判定定理法,其基本思路是:连接过这点的半径,证明这条半径与直线垂直即可,可简述为:有切点,连半径,证垂直;(2)若未知直线与圆有公共点,则采用数量关系法,其基本思路是:过圆心作直线的垂线段,证明垂线段的长等于圆的半径,可简述为:无切点,作垂线,证半径.
知4-讲
知识点
切线长定理
4
1. 切线长定义:经过圆外一点作圆的切线,这点和切点之间的线段的长,叫作这点到圆的切线长.
切线是直线,不可度量;切线长是切线上切点与切点外另一点之间的线段的长,可以度量.
知4-讲
2. 切线长定理
过圆外一点所作的圆的两条切线长相等,圆心和这一点的连线平分两条切线的夹角.
特别提醒:
经过圆上一点作圆的切线,有且只有一条,过切点的半径垂直于这条切线;经过圆外一点作圆的切线,有两条,这点和两个切点所连的两条线段相等.
知4-讲
3. 示例
如图2.5-7 是切线长定理的一个基本图形, 可以直接得到结论:
(1)PO ⊥ AB;(2)AO ⊥ AP,BO ⊥ BP;
(3)AP=BP;(4)∠ 1= ∠ 2= ∠ 3= ∠ 4;
(5)AD=BD;
(6)3= BC 等.
︵
知4-讲
如图2.5-8,PA,PB,DE 分别切⊙ O 于点A,B,C,点D在PA 上,点E 在PB 上.
例 7
知4-讲
图解:
如图2.5-9,利用切线长定理,可将求△ PDE 的周长转化为求PA 与PB 的和.
知4-讲
(1)若PA=10,求△ PDE 的周长;
解题秘方:根据切线长的定义,判断出PA,PB,DA,DC,EC,EB 的长都是切线长,再利用切线长定理,找到相等关系.
知4-讲
解:∵ PA,PB,DE 分别切⊙ O 于点A,B,C,
∴ PA=PB,DA=DC,EC=EB.
∴ PD+DE+PE=PD+DA+EB+PE=PA+PB=10+10=20.
∴△ PDE 的周长为20.
知4-讲
(2)若∠ P=50°,求∠ DOE 的度数.
解题秘方:根据切线长的定义,判断出PA,PB,DA,DC,EC,EB 的长都是切线长,再利用切线长定理,找到相等关系.
知4-讲
解:如图2.5-8,连接OA,OC,OB.
∵ PA,PB,DE 是⊙ O 的切线,
∴ OA ⊥ PA,OB ⊥ PB,OC ⊥ DE.
∴∠ DAO= ∠ EBO=90° . ∴∠ P+ ∠ AOB=180° .
∴∠ AOB=180°- 50° =130° .
易知∠ AOD= ∠ DOC,∠ COE= ∠ BOE,
∴∠ DOE= ∠ AOB= ×130°=65°
知4-讲
详解:
由于点D到OA,OC的距离相等,点E到OB,OC 的距离相等,根据在角的内部,到角两边距离相等的点在角的平分线上,可知点D,E分别在∠ AOC,∠ BOC 的平分线上.
知4-讲
如图2.5-10,PA,PB 是⊙ O 的切线,切点分别为A,B,BC 为⊙ O 的直径,连接AB,AC,OP.
例8
知4-讲
求证:(1)∠ APB = 2 ∠ ABC;
解题秘方:活用切线长定理中角的关系结合相关性质求解.
知4-讲
证明:∵ PA,PB 分别切⊙ O 于点A,B,
∴由切线长定理知∠ BPO= ∠ APO= ∠ APB,PA=PB.
∴ PO ⊥ AB. ∴∠ ABP+ ∠ BPO=90° .
又∵ PB 是⊙ O 的切线,∴ OB ⊥ PB.
∴∠ ABP+ ∠ ABC=90° .
∴∠ ABC= ∠ BPO= ∠ APB,即∠ APB=2 ∠ ABC.
知4-讲
(2) AC ∥ OP.
解题秘方:活用切线长定理中角的关系结合相关性质求解.
知4-讲
证明:∵ BC 是⊙ O 的直径,
∴∠ BAC=90°,即AC ⊥ AB.
由(1)知OP ⊥ AB,∴ AC ∥ OP.
知4-讲
特别提醒:
切线长定理揭示了两个方面的内容,一是切线长相等,揭示线段之间的数量关系;二是圆外一点与圆心的连线平分两条切线的夹角,揭示了角之间的数量关系. 这两个方面的内容为证明线段之间的关系或者角之间的关系提供了大量的条件.
知5-讲
知识点
三角形的内切圆
5
1. 三角形的内切圆:与三角形各边都相切的圆叫作三角形的内切圆,内切圆的圆心叫作三角形的内心,这个三角形叫作圆的外切三角形.
要点解读:
1. “内切“” 外切”是针对位置而言的, “内”是相对于三角形而言, “外”是相对于圆而言.
2. 一个三角形有且只有一个内切圆,而一个圆有无数多个外切三角形.
3. 三角形的内心在三角形的内部.在实际操作中,画出三角形任意两个内角的平分线,找到交点,该交点就是三角形的内心.
知5-讲
2. 三角形的内心:三角形的内心是这个三角形的三条角平分线的交点.三角形内心的性质:三角形的内心到三角形三条边的距离都相等,且等于其内切圆的半径.拓宽视野:如图2.5-11,△ ABC 的周长是l,
内切圆⊙ O 的半径为r.
知5-讲
设BC=a,AC=b,AB=c,则S△ ABC=S△ BOC+
S△ AOC+S△ AOB= ar+ br+ cr= (a+b+c)r=
lr.
故三角形的面积可以用三角形的周长与其内切圆半径之积的一半表示.
知5-讲
a,b,c 分别是Rt △ ABC 的三边BC,AC,AB 的长,其中∠ C=90°,求此三角形内切圆的半径.
例 7
知5-讲
特别提醒:
用直角三角形三边长表示其内切圆半径的两种方法:r= 或r= (其中a,b 为直角边长,r 为圆的半径,c 为斜边长,S 是直角三角形的面积).
知5-讲
解题秘方一:将Rt△ABC内切圆的半径转化到Rt △ABC的边上,然后借助切线长定理进行线段间的转化.
知5-讲
解法一:如图2.5-12,设Rt △ ABC 的内切圆⊙ O 的半径为r,⊙ O 分别切AB,BC,AC 于点D,E,F,连接OD,OE,OF,则四边形OECF为正方形.
∴ CE=CF=r. ∴ AF=AD=b-r,BD=BE=a-r.
∵ AD+BD=AB,即b-r+a-r=c,∴ r=
知5-讲
解法二:如图2.5-13,设Rt △ ABC 的内切圆⊙ O 的半径为r,连接OA,OB,OC.
由S △ ABC=S △ AOB+S △ AOC+S △ BOC,
得 ab= (a+b+c)r.
故r= .
解题秘方二:利用等积法求解
知5-讲
如图2.5-14,在△ ABC 中,∠ A=80°,点O 是△ ABC 的内心,求∠ BOC 的度数.
例10
知5-讲
特别提醒:
如图2.5-15 是数学中一个典型的基本图形.在△ABC中,若点P是△ABC的内心,则∠BPC=90°+
∠A;若点P是△ABC的外心,
则∠ BPC=2 ∠ A.
知5-讲
解题秘方:三角形的内心是三角形三个内角的平分线的交点.
知5-讲
解:∵∠ A=80°,
∴∠ ABC+ ∠ ACB=180°-80°=100°.
∵点O 是△ ABC 的内心,
∴∠ OBC= ∠ ABC,∠ OCB= ∠ ACB.
∴∠ OBC+ ∠ OCB= (∠ ABC+ ∠ ACB)=50°.
∴∠ BOC=180°-50°=130°.
直线与圆的位置关系
