第七节 生产和生活中的机械能守恒练习(Word版含解析)
文档属性
| 名称 | 第七节 生产和生活中的机械能守恒练习(Word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 169.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 粤教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-12-02 20:07:33 | ||
图片预览




文档简介
第四章 机械能及其守恒定律
第七节 生产和生活中的机械能守恒
基础过关练
题组一 落锤打桩机
1.图甲是一台打桩机的简易模型,桩柱B静止在水平地面,重锤A在绳子拉力作用下从桩柱上端由静止上升,当重锤上升4.2 m时,撤去拉力F,重锤继续上升0.8 m后自由下落,并与桩柱撞击,撞击后将桩柱打入地下一定深度。已知重锤的质量m=42 kg、桩柱的质量M=168 kg。重锤上升过程中其动能随上升高度的变化规律如图乙所示,重锤和桩柱撞击时间极短,滑轮离地足够高,不计空气阻力和滑轮的摩擦,重力加速度g=10 m/s2。试求:
(1)重锤从最高点落回桩柱B上端所用的时间和重锤落回到桩柱B上端时的速度大小;
(2)撤去拉力F前,拉力F做功的平均功率。
题组二 跳台滑雪
2.(2021湖南永州高三月考)跳台滑雪就是运动员脚着特制的滑雪板,沿着跳台的倾斜助滑道下滑,借助速度和弹跳力,使身体跃入空中,运动员在空中飞行4~5秒钟后,落在山坡上。为研究跳台滑雪,将某次跳台滑雪简化为如下过程:质量为60 kg的运动员在助滑道末端沿水平方向跃入空中,经过4 s落在斜坡上。则在空中飞行过程中(忽略空气阻力,取g=10 m/s2) ( )
A.运动员处于超重状态
B.运动员落在斜坡前瞬间重力的功率为1.2×104 W
C.运动员动能增加9.6×104 J
D.运动员重力势能减少4.8×104 J
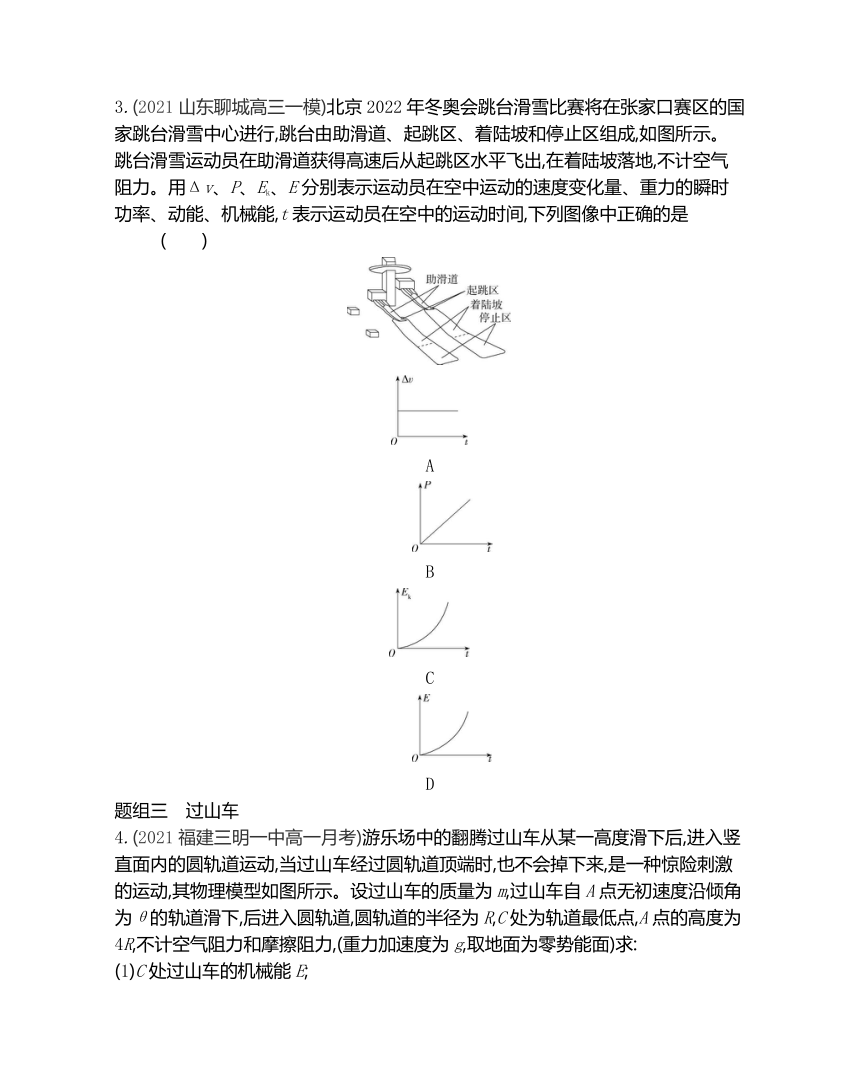
3.(2021山东聊城高三一模)北京2022年冬奥会跳台滑雪比赛将在张家口赛区的国家跳台滑雪中心进行,跳台由助滑道、起跳区、着陆坡和停止区组成,如图所示。跳台滑雪运动员在助滑道获得高速后从起跳区水平飞出,在着陆坡落地,不计空气阻力。用Δv、P、Ek、E分别表示运动员在空中运动的速度变化量、重力的瞬时功率、动能、机械能,t表示运动员在空中的运动时间,下列图像中正确的是 ( )
A
B
C
D
题组三 过山车
4.(2021福建三明一中高一月考)游乐场中的翻腾过山车从某一高度滑下后,进入竖直面内的圆轨道运动,当过山车经过圆轨道顶端时,也不会掉下来,是一种惊险刺激的运动,其物理模型如图所示。设过山车的质量为m,过山车自A点无初速度沿倾角为θ的轨道滑下,后进入圆轨道,圆轨道的半径为R,C处为轨道最低点,A点的高度为4R,不计空气阻力和摩擦阻力,(重力加速度为g,取地面为零势能面)求:
(1)C处过山车的机械能E;
(2)下滑过程中过山车重力势能等于动能时的高度h;
(3)过山车到圆轨道最高点B时的速度v大小。
能力提升练
题组一 应用动能定理解决打桩机问题
1.()小军看到打桩机,对打桩机的工作原理产生了兴趣。他构建了一个打桩机的简易模型,如图甲所示。他设想,用大小恒定的拉力F拉动绳端B,使物体从A点(与钉子接触处)由静止开始运动,上升一段高度后撤去F,物体运动到最高点后自由下落并撞击钉子,将钉子打入一定深度。按此模型分析,若物体质量m=1 kg,上升1 m高度时撤去拉力,撤去拉力前物体的动能Ek与上升高度h的关系图像如图乙所示。(g取10 m/s2,不计空气阻力)
(1)求物体上升到0.4 m高度处时F的瞬时功率;
(2)若物体撞击钉子后瞬间弹起,且使其不再落下,钉子获得20 J的动能向下运动,钉子总长为10 cm,撞击前插入部分可以忽略,不计钉子重力,已知钉子在插入过程中所受的阻力f与深度x的关系图像如图丙所示,求钉子能够插入的最大深度。深度解析
2.()吊锤打桩机如图a,其工作过程可以简化为图b,质量m=2.0×103 kg的吊锤在绳子的恒定拉力F作用下从与钉子接触处由静止开始运动,上升一段高度后撤去F,到最高点后自由落下,撞击钉子将钉子打入一定深度。吊锤上升过程中,机械能E与上升高度h的关系如图c,不计摩擦及空气阻力,g=10 m/s2。求:
(1)吊锤上升h1=1.6 m时的速度大小;
(2)吊锤上升h1=1.6 m后,再经过多长时间撞击钉子;
(3)吊锤上升h2=0.4 m时,拉力F的瞬时功率。
题组二 应用动能定理解决跳台滑雪问题
3.(2021四川泸县第四中学高二月考,)跳台滑雪是利用自然山形建成的跳台进行的滑雪运动之一,起源于挪威。运动员脚着特制的滑雪板,沿着跳台的倾斜助滑道下滑,借助下滑速度和弹跳力,使身体跃入空中,在空中飞行约4~5秒钟后,落在山坡上。某滑雪运动员(可视为质点)由坡道进入竖直面内的圆弧形滑道AB,从滑道的A点滑行到最低点B的过程中,由于摩擦力的存在,运动员的速率不变,则运动员沿AB下滑过程中 ( )
A.所受合外力始终为零
B.所受摩擦力大小不变
C.合外力做功一定为零
D.机械能始终保持不变
4.(2021四川内江高三二模,)2022年第24届冬季奥林匹克运动会将在北京和张家口举行,跳台滑雪是其中最具观赏性的项目之一。如图所示为跳台滑雪赛道的简化图,由助滑道、起跳区、着陆坡等几段组成,助滑道和着陆坡与水平面的夹角θ均为37°,直线AB段长度L=100 m,运动员连同装备总质量m=60 kg,由A点无初速度下滑,从起跳区的C点起跳后降落在着陆坡上的D点。将运动员和滑雪板整体看作质点,不计空气阻力,重力加速度g=10 m/s2,sin 37°=0.6,cos 37°=0.8。
(1)若运动员下滑到B点的速度大小为30 m/s,求助滑道对滑雪板的摩擦力对滑雪板所做的功;
(2)若运动员从C点起跳时的速度沿水平方向,测得C、D间的距离为 m,求运动员在C处的速度大小。
题组三 应用动能定理解决过山车问题
5.(2021江苏镇江高二月考,)过山车是一种惊险的游乐项目,其运动轨道可视为如图所示的物理模型。已知轨道最高点A离地面高为20 m,圆环轨道半径为5 m,过山车质量为50 kg,g=10 m/s2,求:
(1)若不计一切阻力,过山车从A点静止释放后,经过最低点B时的速度为多大
(2)若不计一切阻力,当过山车经过圆形轨道最高点C时,轨道对车的作用力为多大
(3)若考虑阻力的影响,当过山车经过C点时对轨道恰好无压力,则在过山车从A点运动至C点的过程中,克服阻力做的功为多大
6.(2021浙江杭州高一期中,)如图1所示,游乐场的过山车可以底朝上在竖直圆轨道上运行,可抽象为图2的模型,倾角为45°的直轨道AB、半径R=10 m的光滑竖直圆轨道和倾角为37°的直轨道EF,分别通过水平光滑衔接轨道BC、C'E平滑连接,另有水平减速直轨道FG与EF平滑连接,E、G间的水平距离l=40 m。现有质量m=500 kg的过山车,从高h=40 m的A点由静止下滑,经B、C、D、C'、E、F最终停在G点,过山车与轨道AB、EF间的动摩擦因数均为μ1=0.2,与减速直轨道FG间的动摩擦因数为μ2=0.75,过山车可视为质点,运动中不脱离轨道,g=10 m/s2,求:
(1)过山车运动至圆轨道最低点C时的速度大小;
(2)过山车运动至圆轨道最高点D时对轨道的作用力大小;
(3)减速直轨道FG的长度x。(已知sin 37°=0.6,cos 37°=0.8)
答案全解全析
第四章 机械能及其守恒定律
第七节 生产和生活中的机械能守恒
基础过关练
1.答案 (1)1 s 10 m/s (2)1 000 W
解析 (1)重锤上升的最大高度为H=(4.2+0.8) m=5.0 m
根据自由落体运动的规律可得H=gt2
重锤落回到桩柱B上端时的速度v1=
解得v1=10 m/s,t=1 s
(2)撤去拉力前,重锤匀加速上升,由动能定理可得
(F-mg)h1=Ek1
又有Ek1=mv2,=F·,解得=1 000 W
2.D 由于运动员在空中飞行过程中只受重力,加速度向下,故处于失重状态,选项A错误;运动员落在斜坡前瞬间竖直分速度vy=gt=40 m/s,因此重力的功率P=mgvy=2.4×104 W,选项B错误;这段时间下落的高度h=gt2=80 m,根据机械能守恒定律,运动员动能的增量ΔEk=mgh=4.8×104 J,选项C错误;重力势能减少量ΔEp=mgh=4.8×104 J,选项D正确。
3.B 运动员在空中做平抛运动,则竖直方向的加速度为g,则Δv=gt,选项A错误;重力的瞬时功率P=mgvy=mg2t,选项B正确;某时刻的动能Ek=m+mgh=m+mg2t2,选项C错误;平抛物体的机械能守恒,则E-t图像是平行t轴的直线,选项D错误。
4.答案 (1)4mgR (2)2R (3)2
解析 (1)下滑过程中过山车机械能守恒,则EC=EA=mgH+0=4mgR。
(2)从开始下滑到重力势能等于动能的过程中过山车的机械能守恒
mgH+0=Ek+mgh
Ek=mgh
解得h==2R
(3)从A到B过程中过山车机械能守恒
mgH+0=mg·2R+mv2
解得v=2
能力提升练
1.答案 (1)120 W (2)0.02 m
解析 (1)撤去F前,根据动能定理,有(F-mg)h=Ek-0
由题图乙得,图线斜率为k=F-mg=20 N
代入数据解得F=30 N
又由题图乙得h=0.4 m时, Ek=8 J,即mv2=8 J,得v=4 m/s
F的瞬时功率PF=Fv=120 W
(2)碰撞后,对钉子,有-x'=0-E'k,其中E'k=20 J
由于平均阻力是最大阻力的一半,所以==
又由题图丙得k'=105 N/m
代入数据解得x'=0.02 m
方法技巧
解答本题要注意以下两点:
(1)动能与势能之和是物体的机械能,由图乙所示图像可以求出物体上升0.4 m时物体的速度,根据动能定理求得力F的大小,然后代入功率的计算式进行计算;
(2)钉子在插入过程中所受阻力f对钉子做功,数值等于钉子动能的改变,根据动能定理即可求得结果。
2.答案 (1)2 m/s (2)0.8 s (3)2.25×104 W
解析 (1)吊锤上升过程中,由功能关系得ΔE=FΔh
结合图c,计算得F==2.25×104 N
设吊锤上升到h1=1.6 m处时的速度为v1,由动能定理知Fh1-mgh1=m-0
解得v1=2 m/s
(2)依题意,吊锤上升到h1=1.6 m处后做初速度为v1=2 m/s的竖直上抛运动,设经时间t落到钉子上,有-h1=v1t-gt2
代入数据,解得t=0.8 s
(3)设吊锤上升到h2=0.4 m处时的速度为v2,由动能定理得Fh2-mgh2=m-0
解得v2=1 m/s
F的瞬时功率P=Fv2
代入数据解得P=2.25×104 W
3.C 运动员做曲线运动,合力方向与速度方向不共线,所受的合力不为零,选项A错误;运动员在某点所受的摩擦力等于重力沿圆弧该点切线向下的分量,可知运动员沿AB下滑过程中,摩擦力减小,选项B错误;根据动能定理可知,动能的变化量为零,可知合外力做功一定为零,选项C正确;运动员的动能不变,势能减小,则机械能减小,选项D错误。
4.答案 (1)-9 000 J (2) m/s
解析 (1)由动能定理得mgL sin θ+Wf=mv2
代入数据,解得Wf=-9 000 J
(2)设运动员从C点起跳时的速度大小为v1,C、D间距离为s,根据平抛运动的规律,有
s cos θ=v1t
s sin θ=gt2
联立解得t=4 s,v1= m/s
5.答案 (1)20 m/s (2)1 500 N (3)3 750 J
解析 (1)由机械能守恒定律得mgh=mv2
解得v==20 m/s
(2)从A到C的过程中机械能守恒,有mg(h-2r)=m
解得vC==10 m/s
在C点时由牛顿第二定律得F+mg=m
解得F=1 500 N
(3)从A到C的过程中,由动能定理可得
mg(h-2r)-W=mv ①
又因为过山车经过C点时对轨道恰好无压力,所以有
mg=m ②
由①②两式可得:W=3 750 J
6.答案 (1)8 m/s (2)7 000 N (3)30 m
解析 (1)设过山车到达C点的速度为vC,由动能定理得
mgh-μ1mg cos 45°=m
代入数据可得vC=8 m/s
(2)设过山车到达D点的速度为vD,由C到D的过程由机械能守恒定律得
2mgR+m=m
由牛顿第二定律得
mg+FD=m
联立代入数据可得FD=7 000 N
由牛顿第三定律可知,轨道受到的力F'D=7 000 N
(3)过山车从A到达G点,由动能定理可得
mgh-mg(l-x)tan 37°-μ1mgh -μ1mg(l-x)-μ2mgx=0
代入数据可得x=30 m
第七节 生产和生活中的机械能守恒
基础过关练
题组一 落锤打桩机
1.图甲是一台打桩机的简易模型,桩柱B静止在水平地面,重锤A在绳子拉力作用下从桩柱上端由静止上升,当重锤上升4.2 m时,撤去拉力F,重锤继续上升0.8 m后自由下落,并与桩柱撞击,撞击后将桩柱打入地下一定深度。已知重锤的质量m=42 kg、桩柱的质量M=168 kg。重锤上升过程中其动能随上升高度的变化规律如图乙所示,重锤和桩柱撞击时间极短,滑轮离地足够高,不计空气阻力和滑轮的摩擦,重力加速度g=10 m/s2。试求:
(1)重锤从最高点落回桩柱B上端所用的时间和重锤落回到桩柱B上端时的速度大小;
(2)撤去拉力F前,拉力F做功的平均功率。
题组二 跳台滑雪
2.(2021湖南永州高三月考)跳台滑雪就是运动员脚着特制的滑雪板,沿着跳台的倾斜助滑道下滑,借助速度和弹跳力,使身体跃入空中,运动员在空中飞行4~5秒钟后,落在山坡上。为研究跳台滑雪,将某次跳台滑雪简化为如下过程:质量为60 kg的运动员在助滑道末端沿水平方向跃入空中,经过4 s落在斜坡上。则在空中飞行过程中(忽略空气阻力,取g=10 m/s2) ( )
A.运动员处于超重状态
B.运动员落在斜坡前瞬间重力的功率为1.2×104 W
C.运动员动能增加9.6×104 J
D.运动员重力势能减少4.8×104 J
3.(2021山东聊城高三一模)北京2022年冬奥会跳台滑雪比赛将在张家口赛区的国家跳台滑雪中心进行,跳台由助滑道、起跳区、着陆坡和停止区组成,如图所示。跳台滑雪运动员在助滑道获得高速后从起跳区水平飞出,在着陆坡落地,不计空气阻力。用Δv、P、Ek、E分别表示运动员在空中运动的速度变化量、重力的瞬时功率、动能、机械能,t表示运动员在空中的运动时间,下列图像中正确的是 ( )
A
B
C
D
题组三 过山车
4.(2021福建三明一中高一月考)游乐场中的翻腾过山车从某一高度滑下后,进入竖直面内的圆轨道运动,当过山车经过圆轨道顶端时,也不会掉下来,是一种惊险刺激的运动,其物理模型如图所示。设过山车的质量为m,过山车自A点无初速度沿倾角为θ的轨道滑下,后进入圆轨道,圆轨道的半径为R,C处为轨道最低点,A点的高度为4R,不计空气阻力和摩擦阻力,(重力加速度为g,取地面为零势能面)求:
(1)C处过山车的机械能E;
(2)下滑过程中过山车重力势能等于动能时的高度h;
(3)过山车到圆轨道最高点B时的速度v大小。
能力提升练
题组一 应用动能定理解决打桩机问题
1.()小军看到打桩机,对打桩机的工作原理产生了兴趣。他构建了一个打桩机的简易模型,如图甲所示。他设想,用大小恒定的拉力F拉动绳端B,使物体从A点(与钉子接触处)由静止开始运动,上升一段高度后撤去F,物体运动到最高点后自由下落并撞击钉子,将钉子打入一定深度。按此模型分析,若物体质量m=1 kg,上升1 m高度时撤去拉力,撤去拉力前物体的动能Ek与上升高度h的关系图像如图乙所示。(g取10 m/s2,不计空气阻力)
(1)求物体上升到0.4 m高度处时F的瞬时功率;
(2)若物体撞击钉子后瞬间弹起,且使其不再落下,钉子获得20 J的动能向下运动,钉子总长为10 cm,撞击前插入部分可以忽略,不计钉子重力,已知钉子在插入过程中所受的阻力f与深度x的关系图像如图丙所示,求钉子能够插入的最大深度。深度解析
2.()吊锤打桩机如图a,其工作过程可以简化为图b,质量m=2.0×103 kg的吊锤在绳子的恒定拉力F作用下从与钉子接触处由静止开始运动,上升一段高度后撤去F,到最高点后自由落下,撞击钉子将钉子打入一定深度。吊锤上升过程中,机械能E与上升高度h的关系如图c,不计摩擦及空气阻力,g=10 m/s2。求:
(1)吊锤上升h1=1.6 m时的速度大小;
(2)吊锤上升h1=1.6 m后,再经过多长时间撞击钉子;
(3)吊锤上升h2=0.4 m时,拉力F的瞬时功率。
题组二 应用动能定理解决跳台滑雪问题
3.(2021四川泸县第四中学高二月考,)跳台滑雪是利用自然山形建成的跳台进行的滑雪运动之一,起源于挪威。运动员脚着特制的滑雪板,沿着跳台的倾斜助滑道下滑,借助下滑速度和弹跳力,使身体跃入空中,在空中飞行约4~5秒钟后,落在山坡上。某滑雪运动员(可视为质点)由坡道进入竖直面内的圆弧形滑道AB,从滑道的A点滑行到最低点B的过程中,由于摩擦力的存在,运动员的速率不变,则运动员沿AB下滑过程中 ( )
A.所受合外力始终为零
B.所受摩擦力大小不变
C.合外力做功一定为零
D.机械能始终保持不变
4.(2021四川内江高三二模,)2022年第24届冬季奥林匹克运动会将在北京和张家口举行,跳台滑雪是其中最具观赏性的项目之一。如图所示为跳台滑雪赛道的简化图,由助滑道、起跳区、着陆坡等几段组成,助滑道和着陆坡与水平面的夹角θ均为37°,直线AB段长度L=100 m,运动员连同装备总质量m=60 kg,由A点无初速度下滑,从起跳区的C点起跳后降落在着陆坡上的D点。将运动员和滑雪板整体看作质点,不计空气阻力,重力加速度g=10 m/s2,sin 37°=0.6,cos 37°=0.8。
(1)若运动员下滑到B点的速度大小为30 m/s,求助滑道对滑雪板的摩擦力对滑雪板所做的功;
(2)若运动员从C点起跳时的速度沿水平方向,测得C、D间的距离为 m,求运动员在C处的速度大小。
题组三 应用动能定理解决过山车问题
5.(2021江苏镇江高二月考,)过山车是一种惊险的游乐项目,其运动轨道可视为如图所示的物理模型。已知轨道最高点A离地面高为20 m,圆环轨道半径为5 m,过山车质量为50 kg,g=10 m/s2,求:
(1)若不计一切阻力,过山车从A点静止释放后,经过最低点B时的速度为多大
(2)若不计一切阻力,当过山车经过圆形轨道最高点C时,轨道对车的作用力为多大
(3)若考虑阻力的影响,当过山车经过C点时对轨道恰好无压力,则在过山车从A点运动至C点的过程中,克服阻力做的功为多大
6.(2021浙江杭州高一期中,)如图1所示,游乐场的过山车可以底朝上在竖直圆轨道上运行,可抽象为图2的模型,倾角为45°的直轨道AB、半径R=10 m的光滑竖直圆轨道和倾角为37°的直轨道EF,分别通过水平光滑衔接轨道BC、C'E平滑连接,另有水平减速直轨道FG与EF平滑连接,E、G间的水平距离l=40 m。现有质量m=500 kg的过山车,从高h=40 m的A点由静止下滑,经B、C、D、C'、E、F最终停在G点,过山车与轨道AB、EF间的动摩擦因数均为μ1=0.2,与减速直轨道FG间的动摩擦因数为μ2=0.75,过山车可视为质点,运动中不脱离轨道,g=10 m/s2,求:
(1)过山车运动至圆轨道最低点C时的速度大小;
(2)过山车运动至圆轨道最高点D时对轨道的作用力大小;
(3)减速直轨道FG的长度x。(已知sin 37°=0.6,cos 37°=0.8)
答案全解全析
第四章 机械能及其守恒定律
第七节 生产和生活中的机械能守恒
基础过关练
1.答案 (1)1 s 10 m/s (2)1 000 W
解析 (1)重锤上升的最大高度为H=(4.2+0.8) m=5.0 m
根据自由落体运动的规律可得H=gt2
重锤落回到桩柱B上端时的速度v1=
解得v1=10 m/s,t=1 s
(2)撤去拉力前,重锤匀加速上升,由动能定理可得
(F-mg)h1=Ek1
又有Ek1=mv2,=F·,解得=1 000 W
2.D 由于运动员在空中飞行过程中只受重力,加速度向下,故处于失重状态,选项A错误;运动员落在斜坡前瞬间竖直分速度vy=gt=40 m/s,因此重力的功率P=mgvy=2.4×104 W,选项B错误;这段时间下落的高度h=gt2=80 m,根据机械能守恒定律,运动员动能的增量ΔEk=mgh=4.8×104 J,选项C错误;重力势能减少量ΔEp=mgh=4.8×104 J,选项D正确。
3.B 运动员在空中做平抛运动,则竖直方向的加速度为g,则Δv=gt,选项A错误;重力的瞬时功率P=mgvy=mg2t,选项B正确;某时刻的动能Ek=m+mgh=m+mg2t2,选项C错误;平抛物体的机械能守恒,则E-t图像是平行t轴的直线,选项D错误。
4.答案 (1)4mgR (2)2R (3)2
解析 (1)下滑过程中过山车机械能守恒,则EC=EA=mgH+0=4mgR。
(2)从开始下滑到重力势能等于动能的过程中过山车的机械能守恒
mgH+0=Ek+mgh
Ek=mgh
解得h==2R
(3)从A到B过程中过山车机械能守恒
mgH+0=mg·2R+mv2
解得v=2
能力提升练
1.答案 (1)120 W (2)0.02 m
解析 (1)撤去F前,根据动能定理,有(F-mg)h=Ek-0
由题图乙得,图线斜率为k=F-mg=20 N
代入数据解得F=30 N
又由题图乙得h=0.4 m时, Ek=8 J,即mv2=8 J,得v=4 m/s
F的瞬时功率PF=Fv=120 W
(2)碰撞后,对钉子,有-x'=0-E'k,其中E'k=20 J
由于平均阻力是最大阻力的一半,所以==
又由题图丙得k'=105 N/m
代入数据解得x'=0.02 m
方法技巧
解答本题要注意以下两点:
(1)动能与势能之和是物体的机械能,由图乙所示图像可以求出物体上升0.4 m时物体的速度,根据动能定理求得力F的大小,然后代入功率的计算式进行计算;
(2)钉子在插入过程中所受阻力f对钉子做功,数值等于钉子动能的改变,根据动能定理即可求得结果。
2.答案 (1)2 m/s (2)0.8 s (3)2.25×104 W
解析 (1)吊锤上升过程中,由功能关系得ΔE=FΔh
结合图c,计算得F==2.25×104 N
设吊锤上升到h1=1.6 m处时的速度为v1,由动能定理知Fh1-mgh1=m-0
解得v1=2 m/s
(2)依题意,吊锤上升到h1=1.6 m处后做初速度为v1=2 m/s的竖直上抛运动,设经时间t落到钉子上,有-h1=v1t-gt2
代入数据,解得t=0.8 s
(3)设吊锤上升到h2=0.4 m处时的速度为v2,由动能定理得Fh2-mgh2=m-0
解得v2=1 m/s
F的瞬时功率P=Fv2
代入数据解得P=2.25×104 W
3.C 运动员做曲线运动,合力方向与速度方向不共线,所受的合力不为零,选项A错误;运动员在某点所受的摩擦力等于重力沿圆弧该点切线向下的分量,可知运动员沿AB下滑过程中,摩擦力减小,选项B错误;根据动能定理可知,动能的变化量为零,可知合外力做功一定为零,选项C正确;运动员的动能不变,势能减小,则机械能减小,选项D错误。
4.答案 (1)-9 000 J (2) m/s
解析 (1)由动能定理得mgL sin θ+Wf=mv2
代入数据,解得Wf=-9 000 J
(2)设运动员从C点起跳时的速度大小为v1,C、D间距离为s,根据平抛运动的规律,有
s cos θ=v1t
s sin θ=gt2
联立解得t=4 s,v1= m/s
5.答案 (1)20 m/s (2)1 500 N (3)3 750 J
解析 (1)由机械能守恒定律得mgh=mv2
解得v==20 m/s
(2)从A到C的过程中机械能守恒,有mg(h-2r)=m
解得vC==10 m/s
在C点时由牛顿第二定律得F+mg=m
解得F=1 500 N
(3)从A到C的过程中,由动能定理可得
mg(h-2r)-W=mv ①
又因为过山车经过C点时对轨道恰好无压力,所以有
mg=m ②
由①②两式可得:W=3 750 J
6.答案 (1)8 m/s (2)7 000 N (3)30 m
解析 (1)设过山车到达C点的速度为vC,由动能定理得
mgh-μ1mg cos 45°=m
代入数据可得vC=8 m/s
(2)设过山车到达D点的速度为vD,由C到D的过程由机械能守恒定律得
2mgR+m=m
由牛顿第二定律得
mg+FD=m
联立代入数据可得FD=7 000 N
由牛顿第三定律可知,轨道受到的力F'D=7 000 N
(3)过山车从A到达G点,由动能定理可得
mgh-mg(l-x)tan 37°-μ1mgh -μ1mg(l-x)-μ2mgx=0
代入数据可得x=30 m
同课章节目录
- 第一章 抛体运动
- 第一节 曲线运动
- 第二节 运动的合成与分解
- 第三节 平抛运动
- 第四节 生活和生产中的抛体运动
- 第二章 圆周运动
- 第一节 匀速圆周运动
- 第二节 向心力与向心加速度
- 第三节 生活中的圆周运动
- 第四节 离心现象及其应用
- 第三章 万有引力定律
- 第一节 认识天体运动
- 第二节 认识万有引力定律
- 第三节 万有引力定律的应用
- 第四节 宇宙速度与航天
- 第四章 机械能及其守恒定律
- 第一节 功
- 第二节 功率
- 第三节 动能 动能定理
- 第四节 势能
- 第五节 机械能守恒定律
- 第六节 验证机械能守恒定律
- 第七节 生产和生活中的机械能守恒
- 第五章 牛顿力学的局限性与相对论初步
- 第一节 牛顿力学的成就与局限性
- 第二节 相对论时空观
- 第三节 宇宙起源和演化
