湘教版九年级下册 2.7正多边形与圆 课件(共24张)
文档属性
| 名称 | 湘教版九年级下册 2.7正多边形与圆 课件(共24张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-03 19:35:26 | ||
图片预览








文档简介
(共24张PPT)
2.7 正多边形与圆
第2章 圆
知识点
正多边形及有关概念
知1-讲
1
1. 正多边形:各边相等,各内角也相等的多边形叫作正多边形.
2. 圆的内接正多边形:将一个圆n(n ≥ 3)等分,依次连接各等分点所得的多边形叫作这个圆的内接正多边形,这个圆是这个正多边形的外接圆.
知1-讲
拓宽视野:
1. 圆的外切正n 边形:把一个圆n(n ≥ 3) 等分,经过各等分点作圆的切线,以相邻切线的交点为顶点的n边形是这个圆的外切正n 边形.
2. 任意三角形都有外接圆和内切圆,但是只有正三角形的外接圆和内切圆是同心圆.
3. 任意多边形不一定有外接圆和内切圆,但当多边形是正多边形时,一定有一个外接圆和一个内切圆,并且这两个圆是同心圆.
知1-讲
解读:
“各边相等,各内角相等”是正多边形的两个基本特征,当边数n>3 时,二者必须同时具备,缺一不可,否则多边形就不是正多边形.
知1-讲
3. 正多边形的有关概念
(1) 正多边形的中心:正多边形的外接圆的圆心叫作正多边形的中心.
(2)正多边形的半径:正多边形的外接圆的半径叫作正多边形的半径.
(3)正多边形的中心角:正多边形每一边所对的圆心角叫作正多边形的中心角.
知1-讲
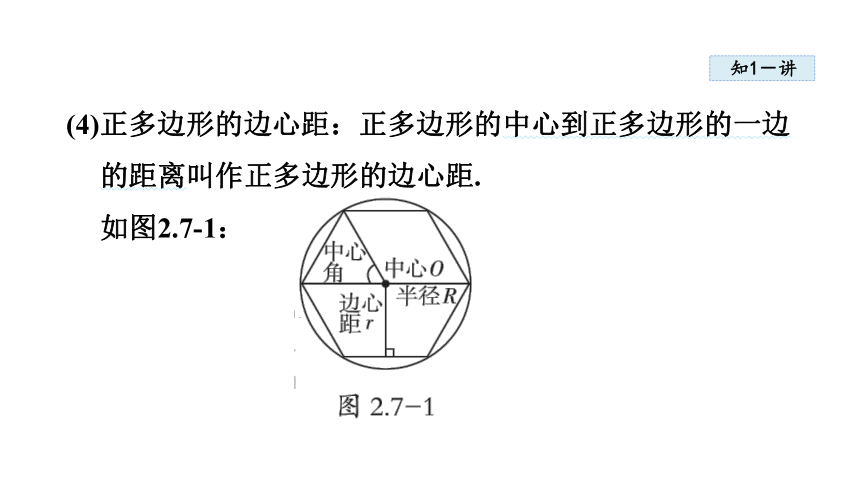
(4)正多边形的边心距:正多边形的中心到正多边形的一边的距离叫作正多边形的边心距.
如图2.7-1:
知1-讲
特别提醒:边心距与弦心距的关系,边心距是正多边形的中心到正多边形一边的距离,也可以看作正多边形的外接圆中,圆心到正多边形的边(即外接圆的弦)的距离,即边心距也是弦心距,但弦心距不一定是边心距.
知1-讲
4. 正多边形的对称性
所有的正多边形都是轴对称图形,一个正n 边形共有n 条对称轴,每条对称轴都通过正n 边形的中心.n 为偶数时,它还是中心对称图形,它的中心就是对称中心.
知1-讲
例 1
如图2.7-2,三角形AOB 是正三角形,以点O 为圆心,OA为半径作⊙ O,直径FC ∥ AB,AO,BO 的延长线分别交⊙ O 于点D,E,求证:
六边形ABCDEF 为圆内接正六边形.
知1-讲
解题秘方:紧扣正多边形的定义,结合同圆中弦、弧、圆心角的关系证明.
解法提醒:
证明一个多边形是圆内接正多边形的方法:
1. 利用正多边形的定义,证明圆内接多边形的每个内角相等,每条边相等;
2. 证明圆内接多边形各边所对的弧相等,即证明这个多边形的各顶点等分这个圆.
知1-讲
证明:∵三角形AOB 是正三角形,∴∠ AOB= ∠OAB= ∠OBA=60°,OB=OA. ∴点B 在⊙ O 上.
∵ FC∥AB,∴∠FOA= ∠OAB=60°,∠COB=
∠OBA=60°.∴∠AOB= ∠BOC= ∠COD= ∠DOE= ∠EOF= ∠FOA=60° .
∴AB=BC=CD=DE=EF=FA . ∴ AB=BC=CD=DE=EF=FA.
∴六边形ABCDEF 为圆内接正六边形.
知2-讲
知识点
正多边形的有关计算
2
正n边形的每个内角都等于 .
正n边形的每个中心角都等于 .
正n边形的每个外角都等于 .
设正n边形的半径为R,边长为a,边心距为r,则:
(1)半径、边长、边心距的关系为R2=r2+ ;
(2)周长l=na;
(3)面积S= ar·n= lr.
知2-讲
特别提醒:
常见的正多边形的边长与半径的关系:
1.正六边形的边长等于其外接圆半径.
2.正三角形的边长等于其外接圆半径的 倍.
3.正方形的边长等于其外接圆半径的 倍.
知2-讲
已知正六边形ABCDEF 的半径为6,求这个正六边形的边长a6,周长l6 和面积S6.
解题秘方:巧用正六边形的边长、半径等关系进行计算.
例2
解法技巧:
构造特殊三角形解正多边形的方法:
在解决有关正六边形和正方形的计算问题时,我们往往作相邻两条半径使其与边分别构成等边三角形和等腰直角三角形,然后与前面学过的勾股定理、垂径定理及切线的性质等知识联系起来综合求解.
知2-讲
解: 如图2.7-3, 设正六边形ABCDEF 的中心为点O, 过点O 作OG ⊥ AB 于点G,连接OA,OB.
∵∠ AOB= =60°,OA=OB,∴∠ AOG=30°.
∴ AG= AO=3. ∴ a6=AB=2AG=6. ∴ l6=
6a6=6×6=36.
知2-讲
在Rt △ AOG 中,OG=
∴ S6= ×AB×OG×6= ×6×3 ×6=54 .
知识点
正多边形的画法
知3-讲
3
正n边形的画法:将圆n等分,然后顺次连接各等分点,即得到所要作的正n边形.
解读:
画正多边形的原理是在同圆中,相等的圆心角所对的弧相等,所对的弦也相等.
知3-讲
1. 用量角器等分圆
先用量角器画一个度数为 的圆心角,则此圆心角所对的弧就是圆的 ,然后在圆周上依次截取这条弧的等弧,就得到圆的n 等
分点,依次连接各等分点,
就得到圆的内接正n 边形,
如图2.7-4 ① .
知3-讲
2. 用尺规等分圆
对于一些特殊的正n边形,如正方形等,可以用圆规和直尺作图. 如图2.7-4 ② .
在⊙ O 中,用直尺和圆规作两条互相
垂直的直径,就可把圆周四等分,从而作
出正四边形,若再逐次平分各边所对的弧,
就可以作边数逐次倍增的正多边形,如正
八边形、正十六边形等.
知3-讲
活学巧记:
每份相等分割圆,
n值大于等于3,
依次连接各分点,
内接正n边形呈现.
解题秘方:紧用量角器画应先求出其中心角,用尺规画则先考虑等分圆周.
知3-讲
作一个正三角形,使其半径为0.9 cm.
特别提醒:
1. 画圆内接正n边形,实质是找圆的n等分点.
2. 用量角器等分圆是一种简单常用的方法,但边数很大时,容易产生较大误差.
3. 尺规作图是一种比较准确的等分圆的方法,但只限于作一些特殊的正多边形.
例 3
知3-讲
解:作法一 (1)作半径为0.9 cm 的⊙ O;
(2)用量角器画∠AOB = ∠BOC=120°,其中A,B,C均为圆上的点;
(3)连接 AB,BC,CA,则
△ABC为所求作的正三角
形, 如图2.7-5.
知3-讲
作法二 (1)作半径为0.9 cm 的⊙ O;
(2)作⊙ O 的任一直径AB;
(3)以B 为圆心,0.9 cm 为半径作弧,
交⊙ O 于D,E;
(4)连接AD,DE,EA,则△ADE为
所求作的正三角形,如图2.7-6.
正多边形与圆
正多边
形与圆
相关概念
有关计算
画法
中心角
中心
半径
边心距
2.7 正多边形与圆
第2章 圆
知识点
正多边形及有关概念
知1-讲
1
1. 正多边形:各边相等,各内角也相等的多边形叫作正多边形.
2. 圆的内接正多边形:将一个圆n(n ≥ 3)等分,依次连接各等分点所得的多边形叫作这个圆的内接正多边形,这个圆是这个正多边形的外接圆.
知1-讲
拓宽视野:
1. 圆的外切正n 边形:把一个圆n(n ≥ 3) 等分,经过各等分点作圆的切线,以相邻切线的交点为顶点的n边形是这个圆的外切正n 边形.
2. 任意三角形都有外接圆和内切圆,但是只有正三角形的外接圆和内切圆是同心圆.
3. 任意多边形不一定有外接圆和内切圆,但当多边形是正多边形时,一定有一个外接圆和一个内切圆,并且这两个圆是同心圆.
知1-讲
解读:
“各边相等,各内角相等”是正多边形的两个基本特征,当边数n>3 时,二者必须同时具备,缺一不可,否则多边形就不是正多边形.
知1-讲
3. 正多边形的有关概念
(1) 正多边形的中心:正多边形的外接圆的圆心叫作正多边形的中心.
(2)正多边形的半径:正多边形的外接圆的半径叫作正多边形的半径.
(3)正多边形的中心角:正多边形每一边所对的圆心角叫作正多边形的中心角.
知1-讲
(4)正多边形的边心距:正多边形的中心到正多边形的一边的距离叫作正多边形的边心距.
如图2.7-1:
知1-讲
特别提醒:边心距与弦心距的关系,边心距是正多边形的中心到正多边形一边的距离,也可以看作正多边形的外接圆中,圆心到正多边形的边(即外接圆的弦)的距离,即边心距也是弦心距,但弦心距不一定是边心距.
知1-讲
4. 正多边形的对称性
所有的正多边形都是轴对称图形,一个正n 边形共有n 条对称轴,每条对称轴都通过正n 边形的中心.n 为偶数时,它还是中心对称图形,它的中心就是对称中心.
知1-讲
例 1
如图2.7-2,三角形AOB 是正三角形,以点O 为圆心,OA为半径作⊙ O,直径FC ∥ AB,AO,BO 的延长线分别交⊙ O 于点D,E,求证:
六边形ABCDEF 为圆内接正六边形.
知1-讲
解题秘方:紧扣正多边形的定义,结合同圆中弦、弧、圆心角的关系证明.
解法提醒:
证明一个多边形是圆内接正多边形的方法:
1. 利用正多边形的定义,证明圆内接多边形的每个内角相等,每条边相等;
2. 证明圆内接多边形各边所对的弧相等,即证明这个多边形的各顶点等分这个圆.
知1-讲
证明:∵三角形AOB 是正三角形,∴∠ AOB= ∠OAB= ∠OBA=60°,OB=OA. ∴点B 在⊙ O 上.
∵ FC∥AB,∴∠FOA= ∠OAB=60°,∠COB=
∠OBA=60°.∴∠AOB= ∠BOC= ∠COD= ∠DOE= ∠EOF= ∠FOA=60° .
∴AB=BC=CD=DE=EF=FA . ∴ AB=BC=CD=DE=EF=FA.
∴六边形ABCDEF 为圆内接正六边形.
知2-讲
知识点
正多边形的有关计算
2
正n边形的每个内角都等于 .
正n边形的每个中心角都等于 .
正n边形的每个外角都等于 .
设正n边形的半径为R,边长为a,边心距为r,则:
(1)半径、边长、边心距的关系为R2=r2+ ;
(2)周长l=na;
(3)面积S= ar·n= lr.
知2-讲
特别提醒:
常见的正多边形的边长与半径的关系:
1.正六边形的边长等于其外接圆半径.
2.正三角形的边长等于其外接圆半径的 倍.
3.正方形的边长等于其外接圆半径的 倍.
知2-讲
已知正六边形ABCDEF 的半径为6,求这个正六边形的边长a6,周长l6 和面积S6.
解题秘方:巧用正六边形的边长、半径等关系进行计算.
例2
解法技巧:
构造特殊三角形解正多边形的方法:
在解决有关正六边形和正方形的计算问题时,我们往往作相邻两条半径使其与边分别构成等边三角形和等腰直角三角形,然后与前面学过的勾股定理、垂径定理及切线的性质等知识联系起来综合求解.
知2-讲
解: 如图2.7-3, 设正六边形ABCDEF 的中心为点O, 过点O 作OG ⊥ AB 于点G,连接OA,OB.
∵∠ AOB= =60°,OA=OB,∴∠ AOG=30°.
∴ AG= AO=3. ∴ a6=AB=2AG=6. ∴ l6=
6a6=6×6=36.
知2-讲
在Rt △ AOG 中,OG=
∴ S6= ×AB×OG×6= ×6×3 ×6=54 .
知识点
正多边形的画法
知3-讲
3
正n边形的画法:将圆n等分,然后顺次连接各等分点,即得到所要作的正n边形.
解读:
画正多边形的原理是在同圆中,相等的圆心角所对的弧相等,所对的弦也相等.
知3-讲
1. 用量角器等分圆
先用量角器画一个度数为 的圆心角,则此圆心角所对的弧就是圆的 ,然后在圆周上依次截取这条弧的等弧,就得到圆的n 等
分点,依次连接各等分点,
就得到圆的内接正n 边形,
如图2.7-4 ① .
知3-讲
2. 用尺规等分圆
对于一些特殊的正n边形,如正方形等,可以用圆规和直尺作图. 如图2.7-4 ② .
在⊙ O 中,用直尺和圆规作两条互相
垂直的直径,就可把圆周四等分,从而作
出正四边形,若再逐次平分各边所对的弧,
就可以作边数逐次倍增的正多边形,如正
八边形、正十六边形等.
知3-讲
活学巧记:
每份相等分割圆,
n值大于等于3,
依次连接各分点,
内接正n边形呈现.
解题秘方:紧用量角器画应先求出其中心角,用尺规画则先考虑等分圆周.
知3-讲
作一个正三角形,使其半径为0.9 cm.
特别提醒:
1. 画圆内接正n边形,实质是找圆的n等分点.
2. 用量角器等分圆是一种简单常用的方法,但边数很大时,容易产生较大误差.
3. 尺规作图是一种比较准确的等分圆的方法,但只限于作一些特殊的正多边形.
例 3
知3-讲
解:作法一 (1)作半径为0.9 cm 的⊙ O;
(2)用量角器画∠AOB = ∠BOC=120°,其中A,B,C均为圆上的点;
(3)连接 AB,BC,CA,则
△ABC为所求作的正三角
形, 如图2.7-5.
知3-讲
作法二 (1)作半径为0.9 cm 的⊙ O;
(2)作⊙ O 的任一直径AB;
(3)以B 为圆心,0.9 cm 为半径作弧,
交⊙ O 于D,E;
(4)连接AD,DE,EA,则△ADE为
所求作的正三角形,如图2.7-6.
正多边形与圆
正多边
形与圆
相关概念
有关计算
画法
中心角
中心
半径
边心距
