利用频率估计概率
图片预览





文档简介
(共23张PPT)
25.3利用频率估计概率
新乡县翟坡中学
段继涛
问题1 某厂打算生产一种中学生使用的笔袋,但无法确定各种颜色的产量.你认为该如何制定生产计划?
活动1
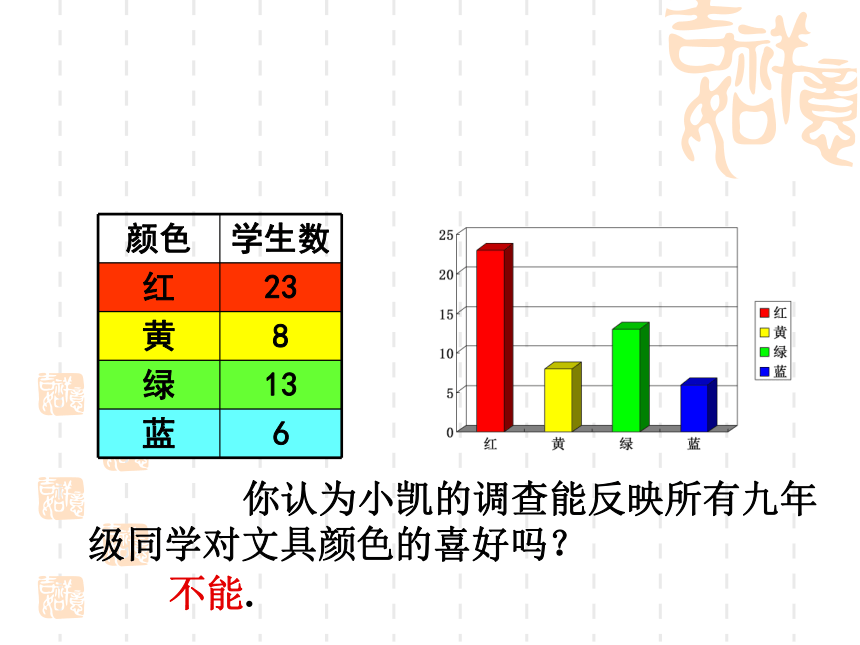
针对中学生喜欢的颜色的问题,小凯调查了九年级某班50位同学,结果如下:
颜色 学生数
红 23
黄 8
绿 13
蓝 6
你认为小凯的调查能反映所有九年级同学对文具颜色的喜好吗?
不能.
为了更为准确地为文具厂商提供信息,你认为抽样调查应注意什么?
抽样调查应更广泛、更有代表性、更有随意性.
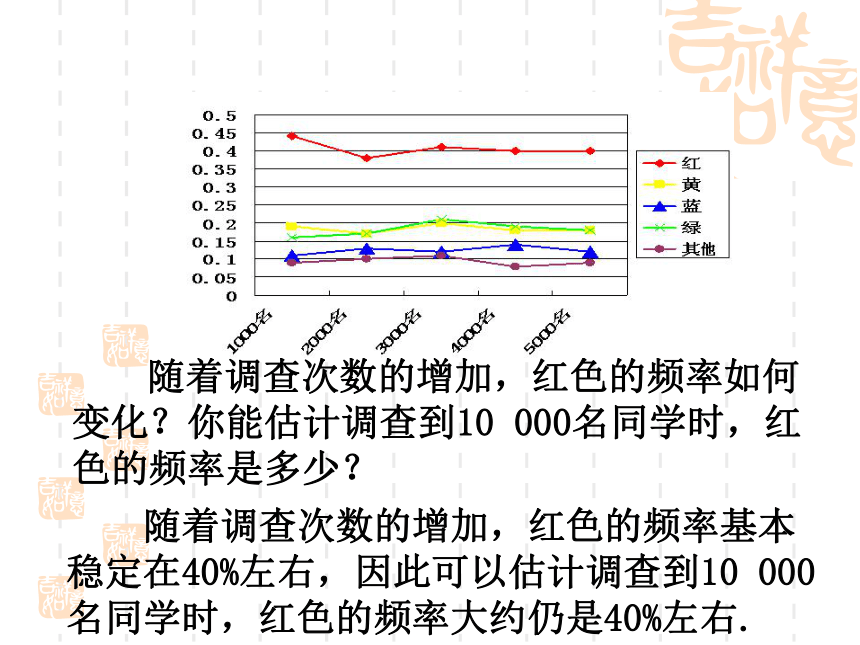
问题2 该文具厂就该笔袋的颜色随机调查了5 000名中学生,并在调查到1 000名、2 000名、3 000名、4 000名、5 000名时分别计算了各种颜色的频率,绘制折线图如下:
随着调查次数的增加,红色的频率基本稳定在40%左右,因此可以估计调查到10 000名同学时,红色的频率大约仍是40%左右.
随着调查次数的增加,红色的频率如何变化?你能估计调查到10 000名同学时,红色的频率是多少?
你认为该文具厂生产这种笔袋时,对颜色应如何安排?
该厂生产这种笔袋时,一般可安排:
生产40%左右的红色,20%左右的绿色,18%左右的黄色,12%左右的蓝色,10%左右的其他颜色.
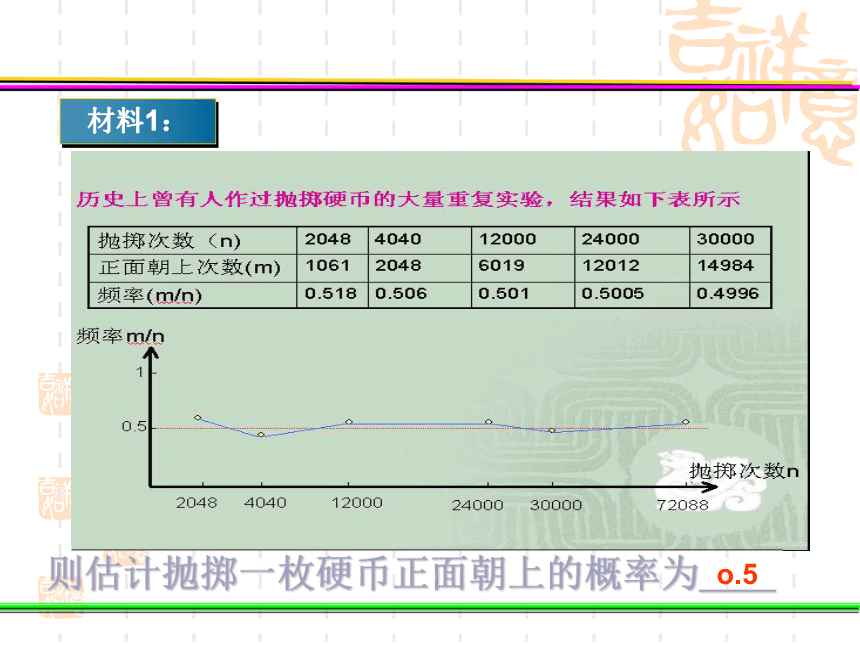
材料1:
则估计抛掷一枚硬币正面朝上的概率为__
o.5
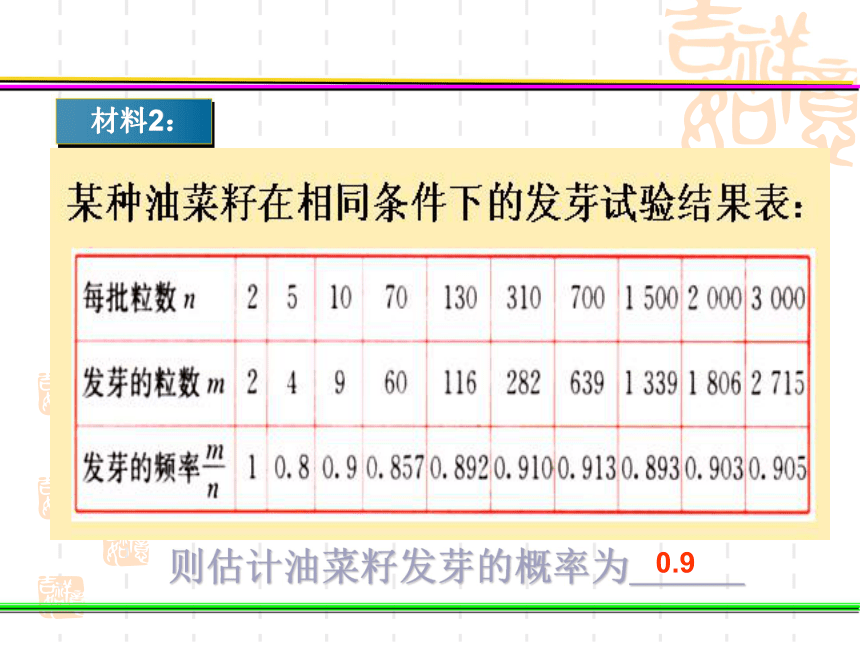
材料2:
则估计油菜籽发芽的概率为___
0.9
结 论
瑞士数学家雅各布.伯努利(1654-1705)最早阐明了可以由频率估计概率即: 在相同的条件下,大量的重复实验时,根据一个随机事件发生的频率所逐渐稳定的常数,可以估计这个事件发生的概率
某林业部门要了解某种幼树在一定条件下的移植成活率,应采取什么具体做法?
活动2
种植总数(n) 成活数(n) 成活的频率
10 8
50 47
270 235
400 369
750 662
1 500 1 335
3 500 3 203
7 000 6 335
9 000 8 073
14 000 12 628
0.8
0.94
0.871
0.923
0.883
0.890
0.915
0.905
0.897
0.902
从表中数据可以发现,幼树移植成活的频率在____左右摆动,并且随着统计数据的增加,这种规律愈加明显,所以估计幼树移植成活的概率为_____.
0.9
0.9
概率伴随着我你他
例2、某水果公司以2元/千克的成本新进了10000千克柑橘,销售人员首先从所有的柑橘中随机地抽取若干柑橘,进行 了“柑橘损坏率“统计,并把获得的数据记录在下表中
柑橘总质量(n)千克 损坏柑橘质量(m)千克 柑橘损坏的频率(m/n)
50 5.50
100 10.50
150 15.15
200 19.42
250 24.35
300 30.32
350 35.32
400 39.24
450 44.57
500 51.54
0.110
0.105
0.101
0.097
0.097
0.101
0.101
0.098
0.099
0.103
1)同桌合作完成表25-6.
(2)根据表中数据填空:
这批柑橘损坏的概率是______,则完好柑橘的概率是_______,
如果某水果公司以2元/千克的成本进了10000千克柑橘,则这批柑橘中完好柑橘的质量是________,若公司希望这些柑橘能够
获利5000元,那么售价应定为_______元/千克比较合适.
0.1
0.9
9000
2.8
问题1 某商场设立了一个可以自由转动的转盘(如图),并规定:顾客购物50元以上能获得一次转动转盘的机会,当转盘停止时,指针落在红色区域就可以获得会员卡一张,请问如果消费超过50元,那么能够得到会员卡的概率是多少?
活动3
概率伴随着我你他
问题2 若商场换了一个自由转动的转盘(如图),并规定:顾客购物50元以上能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品.
概率伴随着我你他
转动转盘的次数n 100 150 200 500 800 1 000
落在“铅笔”的次数m 68 111 136 345 546 701
落在“铅笔”的频率
(2) 请估计,当n很大时,频率将会接近多少?
(3) 转动该转盘一次,获得铅笔的概率约是多少?
(4) 在该转盘中,标有“铅笔”区域的扇形的圆心角大约是多少?(精确到1°)
(1) 计算并完成表格:
0.68
0.74
0.68
0.69
0.6825
0.701
0.69
0.69
0.69×360°≈248°
概率伴随着我你他
(1)试验的次数越多,所得的频率越能反映概率的大小;
(2)频数分布表、扇形图、条形图、直方图都能较好地反映频数、频率的分布情况,我们可以利用它们所提供的信息估计概率.
概率伴随着我你他
1. 某人把50粒黄豆染色后与一袋黄豆充分混匀,接着抓出100粒黄豆,进行大量试验后,被抓出染色黄豆的频率是0.03,则这袋黄豆原来有多少粒?
活动4
概率伴随着我你他
2. 你能估算一粒小米的重量吗?
概率伴随着我你他
小结
学完这节课你有哪些收获?
概率伴随着我你他
结束寄语:
概率是对随机现象的一种数学描述,它可以帮助我们更好地认识随机现象,并对生活中的一些不确定情况作出自己的决策.
从表面上看,随机现象的每一次观察结果都是偶然的,但多次观察某个随机现象,立即可以发现:在大量的偶然之中存在着必然的规律.
25.3利用频率估计概率
新乡县翟坡中学
段继涛
问题1 某厂打算生产一种中学生使用的笔袋,但无法确定各种颜色的产量.你认为该如何制定生产计划?
活动1
针对中学生喜欢的颜色的问题,小凯调查了九年级某班50位同学,结果如下:
颜色 学生数
红 23
黄 8
绿 13
蓝 6
你认为小凯的调查能反映所有九年级同学对文具颜色的喜好吗?
不能.
为了更为准确地为文具厂商提供信息,你认为抽样调查应注意什么?
抽样调查应更广泛、更有代表性、更有随意性.
问题2 该文具厂就该笔袋的颜色随机调查了5 000名中学生,并在调查到1 000名、2 000名、3 000名、4 000名、5 000名时分别计算了各种颜色的频率,绘制折线图如下:
随着调查次数的增加,红色的频率基本稳定在40%左右,因此可以估计调查到10 000名同学时,红色的频率大约仍是40%左右.
随着调查次数的增加,红色的频率如何变化?你能估计调查到10 000名同学时,红色的频率是多少?
你认为该文具厂生产这种笔袋时,对颜色应如何安排?
该厂生产这种笔袋时,一般可安排:
生产40%左右的红色,20%左右的绿色,18%左右的黄色,12%左右的蓝色,10%左右的其他颜色.
材料1:
则估计抛掷一枚硬币正面朝上的概率为__
o.5
材料2:
则估计油菜籽发芽的概率为___
0.9
结 论
瑞士数学家雅各布.伯努利(1654-1705)最早阐明了可以由频率估计概率即: 在相同的条件下,大量的重复实验时,根据一个随机事件发生的频率所逐渐稳定的常数,可以估计这个事件发生的概率
某林业部门要了解某种幼树在一定条件下的移植成活率,应采取什么具体做法?
活动2
种植总数(n) 成活数(n) 成活的频率
10 8
50 47
270 235
400 369
750 662
1 500 1 335
3 500 3 203
7 000 6 335
9 000 8 073
14 000 12 628
0.8
0.94
0.871
0.923
0.883
0.890
0.915
0.905
0.897
0.902
从表中数据可以发现,幼树移植成活的频率在____左右摆动,并且随着统计数据的增加,这种规律愈加明显,所以估计幼树移植成活的概率为_____.
0.9
0.9
概率伴随着我你他
例2、某水果公司以2元/千克的成本新进了10000千克柑橘,销售人员首先从所有的柑橘中随机地抽取若干柑橘,进行 了“柑橘损坏率“统计,并把获得的数据记录在下表中
柑橘总质量(n)千克 损坏柑橘质量(m)千克 柑橘损坏的频率(m/n)
50 5.50
100 10.50
150 15.15
200 19.42
250 24.35
300 30.32
350 35.32
400 39.24
450 44.57
500 51.54
0.110
0.105
0.101
0.097
0.097
0.101
0.101
0.098
0.099
0.103
1)同桌合作完成表25-6.
(2)根据表中数据填空:
这批柑橘损坏的概率是______,则完好柑橘的概率是_______,
如果某水果公司以2元/千克的成本进了10000千克柑橘,则这批柑橘中完好柑橘的质量是________,若公司希望这些柑橘能够
获利5000元,那么售价应定为_______元/千克比较合适.
0.1
0.9
9000
2.8
问题1 某商场设立了一个可以自由转动的转盘(如图),并规定:顾客购物50元以上能获得一次转动转盘的机会,当转盘停止时,指针落在红色区域就可以获得会员卡一张,请问如果消费超过50元,那么能够得到会员卡的概率是多少?
活动3
概率伴随着我你他
问题2 若商场换了一个自由转动的转盘(如图),并规定:顾客购物50元以上能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品.
概率伴随着我你他
转动转盘的次数n 100 150 200 500 800 1 000
落在“铅笔”的次数m 68 111 136 345 546 701
落在“铅笔”的频率
(2) 请估计,当n很大时,频率将会接近多少?
(3) 转动该转盘一次,获得铅笔的概率约是多少?
(4) 在该转盘中,标有“铅笔”区域的扇形的圆心角大约是多少?(精确到1°)
(1) 计算并完成表格:
0.68
0.74
0.68
0.69
0.6825
0.701
0.69
0.69
0.69×360°≈248°
概率伴随着我你他
(1)试验的次数越多,所得的频率越能反映概率的大小;
(2)频数分布表、扇形图、条形图、直方图都能较好地反映频数、频率的分布情况,我们可以利用它们所提供的信息估计概率.
概率伴随着我你他
1. 某人把50粒黄豆染色后与一袋黄豆充分混匀,接着抓出100粒黄豆,进行大量试验后,被抓出染色黄豆的频率是0.03,则这袋黄豆原来有多少粒?
活动4
概率伴随着我你他
2. 你能估算一粒小米的重量吗?
概率伴随着我你他
小结
学完这节课你有哪些收获?
概率伴随着我你他
结束寄语:
概率是对随机现象的一种数学描述,它可以帮助我们更好地认识随机现象,并对生活中的一些不确定情况作出自己的决策.
从表面上看,随机现象的每一次观察结果都是偶然的,但多次观察某个随机现象,立即可以发现:在大量的偶然之中存在着必然的规律.
同课章节目录
