1.4.2用空间向量研究距离、夹角问题 提升训练——2021-2022学年高二上学期数学人教A版(2019)选择性必修第一册(Word含答案解析)
文档属性
| 名称 | 1.4.2用空间向量研究距离、夹角问题 提升训练——2021-2022学年高二上学期数学人教A版(2019)选择性必修第一册(Word含答案解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-06 00:00:00 | ||
图片预览



文档简介
用空间向量研究距离、夹角问题
一、单选题
1.已知直线的方向向量与直线的方向向量,则直线与所成角的余弦值为( )
A. B. C. D.
2.已知二面角α-l-β的两个半平面α与β的法向量分别为a,b,若〈a,b〉=,则二面角α-l-β的大小为( )
A. B.
C.或 D.或
3.已知平面的一个法向量为,则轴与平面所成的角的大小为( )
A. B. C. D.
4.将正方形ABCD沿对角线BD折成直二面角,有如下四个结论:
①;
②是等边三角形;
③AB与平面BCD所成的角为60°;
④AB与CD所成的角为60°.
其中正确的结论是( )
A.①②③ B.②③④ C.①②④ D.①②③④
5.如图,正方体的棱长为1,是底面的中心,则到平面的距离为( )
A. B. C. D.
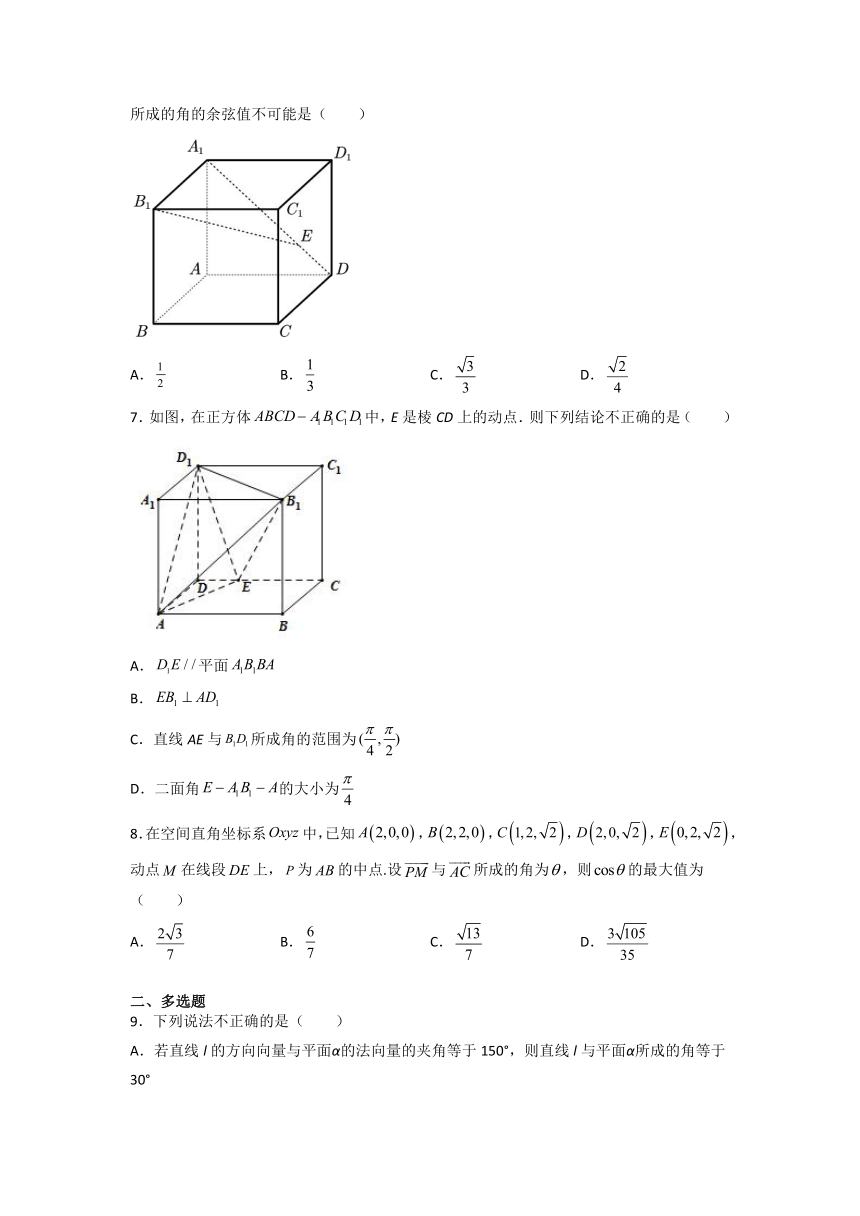
6.如图,在正方体中,为线段上不含端点的动点,则直线与所成的角的余弦值不可能是( )
A. B. C. D.
7.如图,在正方体中,E是棱CD上的动点.则下列结论不正确的是( )
A.平面
B.
C.直线AE与所成角的范围为
D.二面角的大小为
8.在空间直角坐标系中,已知,,,,,动点在线段上,为的中点.设与所成的角为,则的最大值为( )
A. B. C. D.
二、多选题
9.下列说法不正确的是( )
A.若直线l的方向向量与平面α的法向量的夹角等于150°,则直线l与平面α所成的角等于30°
B.两条异面直线的夹角等于它们的方向向量的夹角
C.二面角的大小范围是[0°,180°]
D.二面角的大小等于其两个半平面的法向量的夹角的大小
10.在正方体中,分别是和的中点,则下列结论正确的是( )
A.//平面 B.平面
C. D.点与点到平面的距离相等
11.已知,分别是正方体的棱和的中点,则( )
A.与是异面直线
B.与所成角的大小为
C.与平面所成角的余弦值为
D.二面角的余弦值为
12.三棱锥中,已知平面,且,则下列说法正确的有( )
A. B.平面平面
C.二面角的大小为 D.三棱锥的外接球表面积为
三、填空题
13.若直线的一方向向量与平面的一个法向量的夹角为,则直线与平面所成的角为_________.
14.在正方体ABCD-A1B1C1D1中,E是对角线BD1上的点,且BE∶ED1=1∶3,则AE与平面BCC1B1所成的角的正弦值是___________.
15.已知三棱锥S -ABC中,SA,SB,SC两两垂直,且SA=SB=SC=2,Q是三棱锥S- ABC外接球上一动点,则点Q到平面ABC的距离的最大值为________.
16.若直线a的方向向量为,平面α,β的法向量分别为,则下列命题为真命题的序号是____.
(1)若⊥,则直线a∥平面α;
(2)若∥,则直线a⊥平面α;
(3)若,则直线a与平面α所成角的大小为;
(4)若,则平面α,β的夹角为.
四、解答题
17.如图所示,已知点P在正方体ABCD-A′B′C′D′的对角线BD′上,∠PDA=60°.
(1)求DP与CC′所成角的大小.
(2)求DP与平面AA′D′D所成角的大小.
18.在棱长为1的正方体中,为线段的中点,为线段的中点.
(1)求点到直线的距离;
(2)求直线到平面的距离.
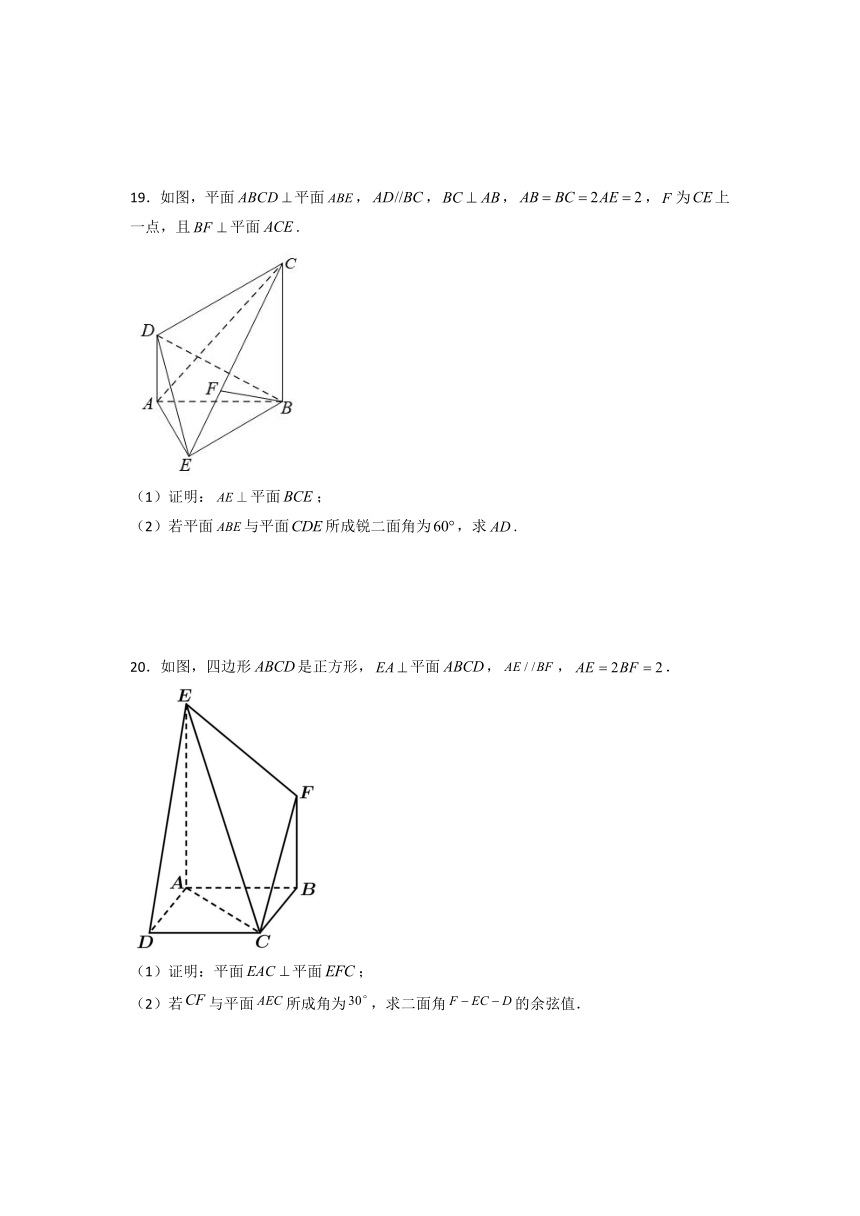
19.如图,平面平面,,,,为上一点,且平面.
(1)证明:平面;
(2)若平面与平面所成锐二面角为,求.
20.如图,四边形是正方形,平面,,.
(1)证明:平面平面;
(2)若与平面所成角为,求二面角的余弦值.
参考答案
1.A
2.C
3.B
4.C
5.D
6.C
如图建立空间直角坐标系,
不妨设正方体的棱长为则
设,
所以
∵直线与所成的角为锐角或直角,
∴
令
所以在单调递增,
易知
则直线与所成的角的余弦值的范围为,
其中.
故选:C.
7.C
对于选项A:因为平面平面,平面,
所以平面,故选项A正确;
如图建立空间直角坐标系,设正方体的棱长为1,则,,
,,,对于选项B:,,
因为,所以,即,
故选项B正确;
对于选项C:,,设直线与所成角为,
则,
当时最大等于,此时最小为,
当时最小等于0,此时最大为,所以,
即直线与所成角的范围为,故选项C不正确;
对于选项D:二面角即二面角,
因为,,
平面,平面,
所以即为二面角的平面角,
在正方形中,,所以二面角的大小为,
故选项D正确,
故选:C.
8.B
设,故,
又,所以,而,
故,其中,
当时,;
当时,,
令,,
故,当且仅当时等号成立,的最大值为,
故选:B.
9.ABD
解:当直线l的方向向量与平面α的法向量的夹角为150°时,直线l与平面α所成的角为60°,A不正确;
向量夹角的范围是[0°,180°],而异面直线夹角为(0°,90°],B不正确;
二面角的范围是[0°,180°],C正确;
二面角的大小与其两个半平面的法向量的夹角的大小相等或互补,D不正确.
故选:ABD.
10.AC
对A,因为分别是和的中点
故,故//平面成立.
对B,建立如图空间直角坐标系,
设正方体边长为2
则,.故.
故不互相垂直.又属于平面.故平面不成立.
对C, ,.
,故成立.
对D,点与点到平面的距离相等则点与点中点在平面上.
连接易得平面即平面.
又点与点中点在上,故点不在平面上.故D不成立.
故选:AC
11.AD
对选项A,由图知:与是异面直线,故A正确;
以为原点,,,分别为,,轴,建立空间直角坐标系,
设正方体边长为,
对选项B,
,,,,
所以,,
设与所成角为,
则,
又因为,所以,故B错误.
对选项C,由题知:平面的法向量为,
因为,,
设与平面所成角为,
则,,故C错误;
对选项D,,,
设平面的法向量,
则,令得,
设平面的法向量,
则,令得,
设二面角的平面角为,
则,
又因为为锐角,所以,故D正确.
故选:AD
12.BCD
若,又由平面,平面,可得,而是平面内两相交直线,得平面,则与平面内直线垂直,这与矛盾,A错;
由平面,平面,知平面平面,B正确;
由平面,平面,可得,同理,而,是平面内两条相交直线,则平面,平面,因此有,过作,垂足为,过作,垂足为,根据二面角的定义知向量的夹角等于二面角,
由已知及题中垂直关系得,,,,,
,
所以,,,因此二面角的大小为,C正确;
由知为三棱锥外接球直径,所以,D正确.
故选:BCD.
13.
14.
15.
由已知,可将三棱锥放入正方体中,其长宽高分别为2,则到面距离最大的点应该在过球心且和面垂直的直径上,因为正方体的外接球直径和正方体的体对角线长相等,则,则到面距离的最大值为,故答案为.
16.(2)(3)(4)
若⊥,则直线a与平面α平行或在平面α内,所以(1)是假命题;
若∥,则也是平面α的法向量,所以直线a⊥平面α,所以(2)是真命题;
直线与平面所成角的正弦值等于直线的方向向量与平面的法向量所成角余弦值的绝对值,所以(3)是真命题;
两个平面的夹角与它们的法向量所成的不大于90°的角相等,所以(4)是真命题.
故答案为:(2)(3)(4).
17.(1)45°.(2)30°.
解:(1)如图所示,
以D为原点,DA,DC,DD′分别为x轴,y轴,z轴正方向建立空间直角坐标系,
设DA=1.则=(1,0,0),=(0,0,1).连接BD,B′D′.在平面BB′D′D中,延长DP交B′D′于H.
设=(m,m,1)(m>0),
由已知<,>=60°,由=||||cos<,>,可得2m=.解得m=,
所以=.
因为cos<,>=
所以<,>=45°,即DP与CC′所成的角为45°.
(2)平面AA′D′D的一个法向量是=(0,1,0),
因为cos<,>=
所以<,>=60°,可得DP与平面AA′D′D所成的角为30°.
18.(1);(2).
解:以为原点,所在直线分别为轴,轴,轴,建立如图所示的空间直角坐标系,
则,
所以,,, .
(1)取,,则.
所以,点到直线的距离为.
(2)因为,所以,所以平面.
所以点到平面的距离为直线到平面的距离.
设平面的法向量为,则
所以
所以
取,则.所以,是平面的一个法向量.
又因为,所以点到平面的距离为.
即直线到平面的距离为.
(1)证明见详解;(2)
证明:
平面,,
又平面平面,
且平面平面,,
所以平面,,
又,平面.
(2)因为平面,,
又,所以
如图所示,过作垂直,以为轴正方向,
以为轴正方向,以为轴,建立空间直角坐标系,
则,,,,,
,,
设为平面的一个法向量,
则,即,
不妨取,解得,,
所以,
显然平面的一个法向量为,
,
解得,故的长为
20.(1)证明见解析;(2).
证明:(1)如图所示:
连接与交于点O,因为为正方形,故,
又平面,故,由,
故平面,
取的中点M,连接,注意到为的中位线,
故,且,
因此,且,
故为平行四边形,即,
因此平面,而平面,
故平面平面.
(2)以A为坐标原点,分别为x,y,z轴,建立空间直角坐标系,
设,
则,
由(1)可知平面,因此平面的一个法向量为,
而,
由与平面所成角为,得,
即,解得;
则,
设平面的一个法向量为,
则得
令,则,故.
设平面的一个法向量,
则得
令,则,,故.
所以,
注意到二面角为钝二面角,
故二面角的余弦值为.
一、单选题
1.已知直线的方向向量与直线的方向向量,则直线与所成角的余弦值为( )
A. B. C. D.
2.已知二面角α-l-β的两个半平面α与β的法向量分别为a,b,若〈a,b〉=,则二面角α-l-β的大小为( )
A. B.
C.或 D.或
3.已知平面的一个法向量为,则轴与平面所成的角的大小为( )
A. B. C. D.
4.将正方形ABCD沿对角线BD折成直二面角,有如下四个结论:
①;
②是等边三角形;
③AB与平面BCD所成的角为60°;
④AB与CD所成的角为60°.
其中正确的结论是( )
A.①②③ B.②③④ C.①②④ D.①②③④
5.如图,正方体的棱长为1,是底面的中心,则到平面的距离为( )
A. B. C. D.
6.如图,在正方体中,为线段上不含端点的动点,则直线与所成的角的余弦值不可能是( )
A. B. C. D.
7.如图,在正方体中,E是棱CD上的动点.则下列结论不正确的是( )
A.平面
B.
C.直线AE与所成角的范围为
D.二面角的大小为
8.在空间直角坐标系中,已知,,,,,动点在线段上,为的中点.设与所成的角为,则的最大值为( )
A. B. C. D.
二、多选题
9.下列说法不正确的是( )
A.若直线l的方向向量与平面α的法向量的夹角等于150°,则直线l与平面α所成的角等于30°
B.两条异面直线的夹角等于它们的方向向量的夹角
C.二面角的大小范围是[0°,180°]
D.二面角的大小等于其两个半平面的法向量的夹角的大小
10.在正方体中,分别是和的中点,则下列结论正确的是( )
A.//平面 B.平面
C. D.点与点到平面的距离相等
11.已知,分别是正方体的棱和的中点,则( )
A.与是异面直线
B.与所成角的大小为
C.与平面所成角的余弦值为
D.二面角的余弦值为
12.三棱锥中,已知平面,且,则下列说法正确的有( )
A. B.平面平面
C.二面角的大小为 D.三棱锥的外接球表面积为
三、填空题
13.若直线的一方向向量与平面的一个法向量的夹角为,则直线与平面所成的角为_________.
14.在正方体ABCD-A1B1C1D1中,E是对角线BD1上的点,且BE∶ED1=1∶3,则AE与平面BCC1B1所成的角的正弦值是___________.
15.已知三棱锥S -ABC中,SA,SB,SC两两垂直,且SA=SB=SC=2,Q是三棱锥S- ABC外接球上一动点,则点Q到平面ABC的距离的最大值为________.
16.若直线a的方向向量为,平面α,β的法向量分别为,则下列命题为真命题的序号是____.
(1)若⊥,则直线a∥平面α;
(2)若∥,则直线a⊥平面α;
(3)若,则直线a与平面α所成角的大小为;
(4)若,则平面α,β的夹角为.
四、解答题
17.如图所示,已知点P在正方体ABCD-A′B′C′D′的对角线BD′上,∠PDA=60°.
(1)求DP与CC′所成角的大小.
(2)求DP与平面AA′D′D所成角的大小.
18.在棱长为1的正方体中,为线段的中点,为线段的中点.
(1)求点到直线的距离;
(2)求直线到平面的距离.
19.如图,平面平面,,,,为上一点,且平面.
(1)证明:平面;
(2)若平面与平面所成锐二面角为,求.
20.如图,四边形是正方形,平面,,.
(1)证明:平面平面;
(2)若与平面所成角为,求二面角的余弦值.
参考答案
1.A
2.C
3.B
4.C
5.D
6.C
如图建立空间直角坐标系,
不妨设正方体的棱长为则
设,
所以
∵直线与所成的角为锐角或直角,
∴
令
所以在单调递增,
易知
则直线与所成的角的余弦值的范围为,
其中.
故选:C.
7.C
对于选项A:因为平面平面,平面,
所以平面,故选项A正确;
如图建立空间直角坐标系,设正方体的棱长为1,则,,
,,,对于选项B:,,
因为,所以,即,
故选项B正确;
对于选项C:,,设直线与所成角为,
则,
当时最大等于,此时最小为,
当时最小等于0,此时最大为,所以,
即直线与所成角的范围为,故选项C不正确;
对于选项D:二面角即二面角,
因为,,
平面,平面,
所以即为二面角的平面角,
在正方形中,,所以二面角的大小为,
故选项D正确,
故选:C.
8.B
设,故,
又,所以,而,
故,其中,
当时,;
当时,,
令,,
故,当且仅当时等号成立,的最大值为,
故选:B.
9.ABD
解:当直线l的方向向量与平面α的法向量的夹角为150°时,直线l与平面α所成的角为60°,A不正确;
向量夹角的范围是[0°,180°],而异面直线夹角为(0°,90°],B不正确;
二面角的范围是[0°,180°],C正确;
二面角的大小与其两个半平面的法向量的夹角的大小相等或互补,D不正确.
故选:ABD.
10.AC
对A,因为分别是和的中点
故,故//平面成立.
对B,建立如图空间直角坐标系,
设正方体边长为2
则,.故.
故不互相垂直.又属于平面.故平面不成立.
对C, ,.
,故成立.
对D,点与点到平面的距离相等则点与点中点在平面上.
连接易得平面即平面.
又点与点中点在上,故点不在平面上.故D不成立.
故选:AC
11.AD
对选项A,由图知:与是异面直线,故A正确;
以为原点,,,分别为,,轴,建立空间直角坐标系,
设正方体边长为,
对选项B,
,,,,
所以,,
设与所成角为,
则,
又因为,所以,故B错误.
对选项C,由题知:平面的法向量为,
因为,,
设与平面所成角为,
则,,故C错误;
对选项D,,,
设平面的法向量,
则,令得,
设平面的法向量,
则,令得,
设二面角的平面角为,
则,
又因为为锐角,所以,故D正确.
故选:AD
12.BCD
若,又由平面,平面,可得,而是平面内两相交直线,得平面,则与平面内直线垂直,这与矛盾,A错;
由平面,平面,知平面平面,B正确;
由平面,平面,可得,同理,而,是平面内两条相交直线,则平面,平面,因此有,过作,垂足为,过作,垂足为,根据二面角的定义知向量的夹角等于二面角,
由已知及题中垂直关系得,,,,,
,
所以,,,因此二面角的大小为,C正确;
由知为三棱锥外接球直径,所以,D正确.
故选:BCD.
13.
14.
15.
由已知,可将三棱锥放入正方体中,其长宽高分别为2,则到面距离最大的点应该在过球心且和面垂直的直径上,因为正方体的外接球直径和正方体的体对角线长相等,则,则到面距离的最大值为,故答案为.
16.(2)(3)(4)
若⊥,则直线a与平面α平行或在平面α内,所以(1)是假命题;
若∥,则也是平面α的法向量,所以直线a⊥平面α,所以(2)是真命题;
直线与平面所成角的正弦值等于直线的方向向量与平面的法向量所成角余弦值的绝对值,所以(3)是真命题;
两个平面的夹角与它们的法向量所成的不大于90°的角相等,所以(4)是真命题.
故答案为:(2)(3)(4).
17.(1)45°.(2)30°.
解:(1)如图所示,
以D为原点,DA,DC,DD′分别为x轴,y轴,z轴正方向建立空间直角坐标系,
设DA=1.则=(1,0,0),=(0,0,1).连接BD,B′D′.在平面BB′D′D中,延长DP交B′D′于H.
设=(m,m,1)(m>0),
由已知<,>=60°,由=||||cos<,>,可得2m=.解得m=,
所以=.
因为cos<,>=
所以<,>=45°,即DP与CC′所成的角为45°.
(2)平面AA′D′D的一个法向量是=(0,1,0),
因为cos<,>=
所以<,>=60°,可得DP与平面AA′D′D所成的角为30°.
18.(1);(2).
解:以为原点,所在直线分别为轴,轴,轴,建立如图所示的空间直角坐标系,
则,
所以,,, .
(1)取,,则.
所以,点到直线的距离为.
(2)因为,所以,所以平面.
所以点到平面的距离为直线到平面的距离.
设平面的法向量为,则
所以
所以
取,则.所以,是平面的一个法向量.
又因为,所以点到平面的距离为.
即直线到平面的距离为.
(1)证明见详解;(2)
证明:
平面,,
又平面平面,
且平面平面,,
所以平面,,
又,平面.
(2)因为平面,,
又,所以
如图所示,过作垂直,以为轴正方向,
以为轴正方向,以为轴,建立空间直角坐标系,
则,,,,,
,,
设为平面的一个法向量,
则,即,
不妨取,解得,,
所以,
显然平面的一个法向量为,
,
解得,故的长为
20.(1)证明见解析;(2).
证明:(1)如图所示:
连接与交于点O,因为为正方形,故,
又平面,故,由,
故平面,
取的中点M,连接,注意到为的中位线,
故,且,
因此,且,
故为平行四边形,即,
因此平面,而平面,
故平面平面.
(2)以A为坐标原点,分别为x,y,z轴,建立空间直角坐标系,
设,
则,
由(1)可知平面,因此平面的一个法向量为,
而,
由与平面所成角为,得,
即,解得;
则,
设平面的一个法向量为,
则得
令,则,故.
设平面的一个法向量,
则得
令,则,,故.
所以,
注意到二面角为钝二面角,
故二面角的余弦值为.
