1.4.2正弦函数、余弦函数的性质(2)课件-2021-2022学年高一上学期数学人教A版必修4(共38张PPT)
文档属性
| 名称 | 1.4.2正弦函数、余弦函数的性质(2)课件-2021-2022学年高一上学期数学人教A版必修4(共38张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-03 16:34:10 | ||
图片预览











文档简介
(共38张PPT)
1.4.2正弦函数、余弦函数的性质(2)
大邑中学数学教研组
1.掌握y=sin x,y=cos x的最大值与最小值,并会求简单三角函数的值域和最值.
2.掌握y=sin x,y=cos x的单调性,并能利用单调性比较大小.
3.会求函数y=Asin(ωx+φ)及y=Acos(ωx+φ)的单调区间.
本节目标
课前预习
(1)正、余弦函数的单调区间分别是什么?
预习课本,思考并完成以下问题
(2)正、余弦函数的最值分别是多少?取最值时自变量x的值是多少?
课前小测
1.函数y=-cos x在区间上是( )
A.增函数 B.减函数
C.先减后增函数 D.先增后减函数
因为y=cos x在区间上先增后减,
所以y=-cos x在区间上先减后增.
C
2.函数y=sin x 的值域为________.
≤sin x≤1
3.函数y=2-sin x取得最大值时x的取值集合为_____________________.
当sin x=-1时,ymax=2-(-1)=3,
此时x=2kπ-,k∈Z.
4.若cos x=m-1有意义,则m的取值范围是________.
所以0≤m≤2.
[0,2]
因为-1≤cos x≤1
要使cos x=m-1有意义,须有-1≤m-1≤1,
新知探究
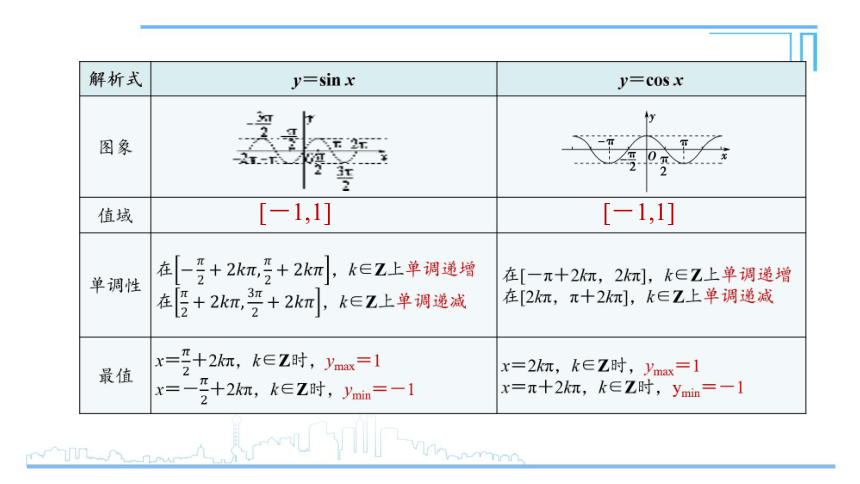
[-1,1]
[-1,1]
思考:y=sin x和y=cos x在区间(m,n)(其中0<m<n<2π)上都是减函数,你能确定m的最小值、n的最大值吗?
提示:由正弦函数和余弦函数的单调性可知m= ,n=π.
题型突破
典例深度剖析 重点多维探究
题型一 正弦函数、余弦函数的单调性
[例1] (1)函数y=cos x在区间[-π,a]上为增函数,则a的取值范围是________.
确定a的范围 → y=cos x在区间[-π,a]上为增函数 → y=cos x在区间[-π,0]上是增函数,在区间[0,π]上是减函数 → a的范围.
思路点拨
题型一 正弦函数、余弦函数的单调性
[例1] (1)函数y=cos x在区间[-π,a]上为增函数,则a的取值范围是________.
y=cos x在[-π,0]上是增函数,在[0,π]上是减函数
所以只有-π<a≤0时满足条件
故a∈(-π,0]
(-π,0]
[例1] (2)已知函数f(x)=,求函数f(x)的单调递增区间.
确定增区间 → 令u= +2x → y= sin u的单调递增区间.
思路点拨
[例1] (2)已知函数f(x)=,求函数f(x)的单调递增区间.
所以函数f(x)= sin +1的单调递增区间是
[-+kπ, +kπ] ,k∈Z.
令u= +2x,
函数y= sin u的单调递增区间为[-+2kπ, +2kπ],k∈Z,
由-+2kπ≤+2x≤ +2kπ,k∈Z,得-+kπ≤x≤ +kπ,k∈Z.
求形如y=Asin(ωx+φ)+b或形如y=Acos(ωx+φ)+b(其中A≠0,ω>0,b为常数)的函数的单调区间时注意两点:
①要把ωx+φ看作一个整体,若ω<0,先用诱导公式将式子变形,将x的系数化为正;
注意:复合函数的单调性遵循“同增异减”的规律.
技法点拨
②在A>0,ω>0时,将“ωx+φ”代入正弦(或余弦)函数的单调区间,可以解得与之单调性一致的单调区间;当A<0,ω>0时同样方法可以求得与正弦(余弦)函数单调性相反的单调区间.
跟踪训练
1.(1)函数y=sin ,x∈的单调递减区间为_____________.
(k∈Z)
(k∈Z)
因为x∈
所以要求的单调递减区间为,
,
跟踪训练
1. (2)已知函数y=cos ,则它的单调减区间为____________________.
y=cos =cos ,
由2kπ≤2x- ≤2kπ+π,k∈Z,
得kπ+ ≤x≤kπ+ ,k∈Z,
∴单调递减区间是[kπ+, kπ+] (k∈Z).
[kπ+, kπ+] (k∈Z)
题型二 利用三角函数的单调性比较大小
[例2] 利用三角函数的单调性,比较下列各组数的大小.
(1) sin与sin;
(2) sin 196°与cos 156°;
(3) cos 与cos .
[例2] 利用三角函数的单调性,比较下列各组数的大小.
(1) sin与sin;
< <
函数y=sinx在[, ]上单调递增
∴sin > sin
[例2] 利用三角函数的单调性,比较下列各组数的大小.
(2) sin 196°与cos 156°;
sin 196°=sin(180°+16°)=-sin 16°,
cos 156°=cos(180°-24°)=-cos 24°=-sin 66°,
∵0°<16°<66°<90°,
∴sin 16°<sin 66°,
从而-sin 16°>-sin 66°,
即sin 196°>cos 156°.
[例2] 利用三角函数的单调性,比较下列各组数的大小.
(3) cos 与cos .
cos =cos π=cos(π)=cos π,
cos =cos π=cos () =cos .
∵0< < π<π,且y=cos x在[0,π]上是减函数,
∴cos π<cos ,
即cos <cos .
1 利用诱导公式,对于正弦函数来说,一般将两个角转化到或内;对于余弦函数来说,一般将两个角转化到[-π,0]或[0,π]内.
2 不同名的函数化为同名的函数.
3 自变量不在同一单调区间化至同一单调区间内,借助正弦、余弦函数的单调性来比较大小.
解题策略
三角函数值大小比较的策略
跟踪训练
2.(1)已知α,β为锐角三角形的两个内角,则以下结论正确的是( )
A.sin α<sin β B.cos α<sin β
C.cos α<cos β D.cos α >cos β
α> -β,α∈(0, ), -β∈ (0, ) ,
α,β为锐角三角形的两个内角,α+β> ,
所以cos α<cos(-β)=sin β.
B
跟踪训练
①cos ,cos ;
cos =cos ,cos =cos ,
因为0< < <π,
而y=cos x在[0,π]上单调递减,
所以cos >cos ,
即cos >cos .
2. (2) 比较下列各组数的大小:
②cos 1,sin 1.
因为cos 1=sin(-1),
而0< -1<1<
且y=sin x在[0, ]上单调递增,
所以sin (-1) <sin 1,
即cos 1<sin 1.
题型三 正弦函数、余弦函数的最值问题
1.函数y=sin(x + )在x∈[0,π]上最小值是多少?
提示:因为x∈[0,π],所以x+∈[, ],由正弦函数图象可知函数的最小值为-.
[探究问题]
题型三 正弦函数、余弦函数的最值问题
[探究问题]
2.函数y=Asin x+b,x∈R的最大值一定是A+b吗?
提示:不是.因为A>0时最大值为A+b,若A<0时最大值应为-A+b.
[例3] (1)函数y=cos2x+2sin x-2,x∈R的值域为________.
y=cos2x+2sin x-2
=-sin2x+2sin x-1=-(sin x-1)2.
因为-1≤sin x≤1,所以-4≤y≤0,
所以函数y=cos2x+2sin x-2,x∈R的值域为[-4,0].
[-4,0]
[例3] (2)已知函数f(x)=asin (2x-) +b(a>0).当x∈ [0, ]时,f(x)的最大值为,最小值是-2,求a和b的值.
∵0≤x≤ ,
∴- ≤sin (2x-) ≤1,
∴- ≤2x- ≤ ,
∴f(x)max=a+b= ,f(x)min=-a+b=-2.
由 得
a+b=
-a+b=-2
a=2
b=-2+
多维探究
变式1 函数y=cos2x+2sin x-2,x∈R,求当函数值取得最小值时x的取值集合.
此时x的取值集合为.
因为y=cos2x+2sin x-2=-sin2x+2sin x-1=-(sin x-1)2,
所以当sin x=-1时,ymin=-4,
变式2 函数y=cos2x+sin x,x∈R的值域为________.
y=cos2x+sin x=1-sin2x+sin x=-(sin x-)2+ .
因为-1≤sin x≤1,
所以-1≤y≤ ,
所以函数y=cos2x+sin x,x∈R的值域为[-1, ].
[-1, ]
1 y=asin2x+bsin x+c a≠0 ,利用换元思想设t=sin x,转化为二次函数y=at2+bt+c求最值,t的范围需要根据定义域来确定.
三角函数最值问题的常见类型及求解方法
2 y=Asin ωx+φ +b,可先由定义域求得ωx+φ的范围,然后求得sin ωx+φ 的范围,最后得最值.
方法总结
随堂检测
1.思考辨析
(1)y=sin x在(0,π)上是增函数.( )
(2)cos 1>cos 2>cos 3.( )
(3)函数y=-sin x,x∈[0, ]的最大值为0.( )
×
√
√
2.y=2cos x2的值域是( )
A.[-2,2] B.[0,2]
C.[-2,0] D.R
因为x∈R,所以x2≥0,
所以y=2cos x2∈[-2,2]
A
3.sin ________sin() (填“>”或“<”).
sin () =sin () =sin ,
因为0< < < ,y=sin x在(0, )上是增函数,
所以sin <sin ,即sin >sin().
>
4.求函数y=1-sin 2x的单调递增区间.
求函数y=1-sin 2x的单调递增区间,
转化为求函数y=sin 2x的单调递减区间,
由+2kπ≤2x≤ +2kπ,k∈Z,得+kπ≤x≤ +kπ,k∈Z,
即函数的单调递增区间是[+kπ, +kπ](k∈Z).
1.确定三角函数单调区间的方法有多种,如换元法、列表法、图象法等,解题时需适当选取,同时要注意,求函数的单调区间必须在这个函数的定义域内进行.
2.函数单调性最基本的应用是比较大小与求值域,求三角函数值域的方法很多,如果函数式中含有多个三角函数式,往往要先将函数式进行变形.
本课小结
1.4.2正弦函数、余弦函数的性质(2)
大邑中学数学教研组
1.掌握y=sin x,y=cos x的最大值与最小值,并会求简单三角函数的值域和最值.
2.掌握y=sin x,y=cos x的单调性,并能利用单调性比较大小.
3.会求函数y=Asin(ωx+φ)及y=Acos(ωx+φ)的单调区间.
本节目标
课前预习
(1)正、余弦函数的单调区间分别是什么?
预习课本,思考并完成以下问题
(2)正、余弦函数的最值分别是多少?取最值时自变量x的值是多少?
课前小测
1.函数y=-cos x在区间上是( )
A.增函数 B.减函数
C.先减后增函数 D.先增后减函数
因为y=cos x在区间上先增后减,
所以y=-cos x在区间上先减后增.
C
2.函数y=sin x 的值域为________.
≤sin x≤1
3.函数y=2-sin x取得最大值时x的取值集合为_____________________.
当sin x=-1时,ymax=2-(-1)=3,
此时x=2kπ-,k∈Z.
4.若cos x=m-1有意义,则m的取值范围是________.
所以0≤m≤2.
[0,2]
因为-1≤cos x≤1
要使cos x=m-1有意义,须有-1≤m-1≤1,
新知探究
[-1,1]
[-1,1]
思考:y=sin x和y=cos x在区间(m,n)(其中0<m<n<2π)上都是减函数,你能确定m的最小值、n的最大值吗?
提示:由正弦函数和余弦函数的单调性可知m= ,n=π.
题型突破
典例深度剖析 重点多维探究
题型一 正弦函数、余弦函数的单调性
[例1] (1)函数y=cos x在区间[-π,a]上为增函数,则a的取值范围是________.
确定a的范围 → y=cos x在区间[-π,a]上为增函数 → y=cos x在区间[-π,0]上是增函数,在区间[0,π]上是减函数 → a的范围.
思路点拨
题型一 正弦函数、余弦函数的单调性
[例1] (1)函数y=cos x在区间[-π,a]上为增函数,则a的取值范围是________.
y=cos x在[-π,0]上是增函数,在[0,π]上是减函数
所以只有-π<a≤0时满足条件
故a∈(-π,0]
(-π,0]
[例1] (2)已知函数f(x)=,求函数f(x)的单调递增区间.
确定增区间 → 令u= +2x → y= sin u的单调递增区间.
思路点拨
[例1] (2)已知函数f(x)=,求函数f(x)的单调递增区间.
所以函数f(x)= sin +1的单调递增区间是
[-+kπ, +kπ] ,k∈Z.
令u= +2x,
函数y= sin u的单调递增区间为[-+2kπ, +2kπ],k∈Z,
由-+2kπ≤+2x≤ +2kπ,k∈Z,得-+kπ≤x≤ +kπ,k∈Z.
求形如y=Asin(ωx+φ)+b或形如y=Acos(ωx+φ)+b(其中A≠0,ω>0,b为常数)的函数的单调区间时注意两点:
①要把ωx+φ看作一个整体,若ω<0,先用诱导公式将式子变形,将x的系数化为正;
注意:复合函数的单调性遵循“同增异减”的规律.
技法点拨
②在A>0,ω>0时,将“ωx+φ”代入正弦(或余弦)函数的单调区间,可以解得与之单调性一致的单调区间;当A<0,ω>0时同样方法可以求得与正弦(余弦)函数单调性相反的单调区间.
跟踪训练
1.(1)函数y=sin ,x∈的单调递减区间为_____________.
(k∈Z)
(k∈Z)
因为x∈
所以要求的单调递减区间为,
,
跟踪训练
1. (2)已知函数y=cos ,则它的单调减区间为____________________.
y=cos =cos ,
由2kπ≤2x- ≤2kπ+π,k∈Z,
得kπ+ ≤x≤kπ+ ,k∈Z,
∴单调递减区间是[kπ+, kπ+] (k∈Z).
[kπ+, kπ+] (k∈Z)
题型二 利用三角函数的单调性比较大小
[例2] 利用三角函数的单调性,比较下列各组数的大小.
(1) sin与sin;
(2) sin 196°与cos 156°;
(3) cos 与cos .
[例2] 利用三角函数的单调性,比较下列各组数的大小.
(1) sin与sin;
< <
函数y=sinx在[, ]上单调递增
∴sin > sin
[例2] 利用三角函数的单调性,比较下列各组数的大小.
(2) sin 196°与cos 156°;
sin 196°=sin(180°+16°)=-sin 16°,
cos 156°=cos(180°-24°)=-cos 24°=-sin 66°,
∵0°<16°<66°<90°,
∴sin 16°<sin 66°,
从而-sin 16°>-sin 66°,
即sin 196°>cos 156°.
[例2] 利用三角函数的单调性,比较下列各组数的大小.
(3) cos 与cos .
cos =cos π=cos(π)=cos π,
cos =cos π=cos () =cos .
∵0< < π<π,且y=cos x在[0,π]上是减函数,
∴cos π<cos ,
即cos <cos .
1 利用诱导公式,对于正弦函数来说,一般将两个角转化到或内;对于余弦函数来说,一般将两个角转化到[-π,0]或[0,π]内.
2 不同名的函数化为同名的函数.
3 自变量不在同一单调区间化至同一单调区间内,借助正弦、余弦函数的单调性来比较大小.
解题策略
三角函数值大小比较的策略
跟踪训练
2.(1)已知α,β为锐角三角形的两个内角,则以下结论正确的是( )
A.sin α<sin β B.cos α<sin β
C.cos α<cos β D.cos α >cos β
α> -β,α∈(0, ), -β∈ (0, ) ,
α,β为锐角三角形的两个内角,α+β> ,
所以cos α<cos(-β)=sin β.
B
跟踪训练
①cos ,cos ;
cos =cos ,cos =cos ,
因为0< < <π,
而y=cos x在[0,π]上单调递减,
所以cos >cos ,
即cos >cos .
2. (2) 比较下列各组数的大小:
②cos 1,sin 1.
因为cos 1=sin(-1),
而0< -1<1<
且y=sin x在[0, ]上单调递增,
所以sin (-1) <sin 1,
即cos 1<sin 1.
题型三 正弦函数、余弦函数的最值问题
1.函数y=sin(x + )在x∈[0,π]上最小值是多少?
提示:因为x∈[0,π],所以x+∈[, ],由正弦函数图象可知函数的最小值为-.
[探究问题]
题型三 正弦函数、余弦函数的最值问题
[探究问题]
2.函数y=Asin x+b,x∈R的最大值一定是A+b吗?
提示:不是.因为A>0时最大值为A+b,若A<0时最大值应为-A+b.
[例3] (1)函数y=cos2x+2sin x-2,x∈R的值域为________.
y=cos2x+2sin x-2
=-sin2x+2sin x-1=-(sin x-1)2.
因为-1≤sin x≤1,所以-4≤y≤0,
所以函数y=cos2x+2sin x-2,x∈R的值域为[-4,0].
[-4,0]
[例3] (2)已知函数f(x)=asin (2x-) +b(a>0).当x∈ [0, ]时,f(x)的最大值为,最小值是-2,求a和b的值.
∵0≤x≤ ,
∴- ≤sin (2x-) ≤1,
∴- ≤2x- ≤ ,
∴f(x)max=a+b= ,f(x)min=-a+b=-2.
由 得
a+b=
-a+b=-2
a=2
b=-2+
多维探究
变式1 函数y=cos2x+2sin x-2,x∈R,求当函数值取得最小值时x的取值集合.
此时x的取值集合为.
因为y=cos2x+2sin x-2=-sin2x+2sin x-1=-(sin x-1)2,
所以当sin x=-1时,ymin=-4,
变式2 函数y=cos2x+sin x,x∈R的值域为________.
y=cos2x+sin x=1-sin2x+sin x=-(sin x-)2+ .
因为-1≤sin x≤1,
所以-1≤y≤ ,
所以函数y=cos2x+sin x,x∈R的值域为[-1, ].
[-1, ]
1 y=asin2x+bsin x+c a≠0 ,利用换元思想设t=sin x,转化为二次函数y=at2+bt+c求最值,t的范围需要根据定义域来确定.
三角函数最值问题的常见类型及求解方法
2 y=Asin ωx+φ +b,可先由定义域求得ωx+φ的范围,然后求得sin ωx+φ 的范围,最后得最值.
方法总结
随堂检测
1.思考辨析
(1)y=sin x在(0,π)上是增函数.( )
(2)cos 1>cos 2>cos 3.( )
(3)函数y=-sin x,x∈[0, ]的最大值为0.( )
×
√
√
2.y=2cos x2的值域是( )
A.[-2,2] B.[0,2]
C.[-2,0] D.R
因为x∈R,所以x2≥0,
所以y=2cos x2∈[-2,2]
A
3.sin ________sin() (填“>”或“<”).
sin () =sin () =sin ,
因为0< < < ,y=sin x在(0, )上是增函数,
所以sin <sin ,即sin >sin().
>
4.求函数y=1-sin 2x的单调递增区间.
求函数y=1-sin 2x的单调递增区间,
转化为求函数y=sin 2x的单调递减区间,
由+2kπ≤2x≤ +2kπ,k∈Z,得+kπ≤x≤ +kπ,k∈Z,
即函数的单调递增区间是[+kπ, +kπ](k∈Z).
1.确定三角函数单调区间的方法有多种,如换元法、列表法、图象法等,解题时需适当选取,同时要注意,求函数的单调区间必须在这个函数的定义域内进行.
2.函数单调性最基本的应用是比较大小与求值域,求三角函数值域的方法很多,如果函数式中含有多个三角函数式,往往要先将函数式进行变形.
本课小结
