人教版 数学六年级上册 6、百分数(一)整理和复习 (课件)(共50张PPT)
文档属性
| 名称 | 人教版 数学六年级上册 6、百分数(一)整理和复习 (课件)(共50张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-02 19:47:13 | ||
图片预览









文档简介
(共50张PPT)
整理和复习
6 百分数(一)
6 百分数(一)
本单元你学习了哪些百分数的知识?这些知识对你来说是完全陌生的吗?
01
单元小结
其实,百分数是一种特殊的分数,在解决实际问题时可以联系分数的实际问题进行思考。
百分数只能表示两个量之间的关系,不能表示一个具体量。
生活中有许多百分数的应用,有的百分数可以超过100%,有的超不过,如发芽率。
求比一个数多(或少)百分之几的数是多少
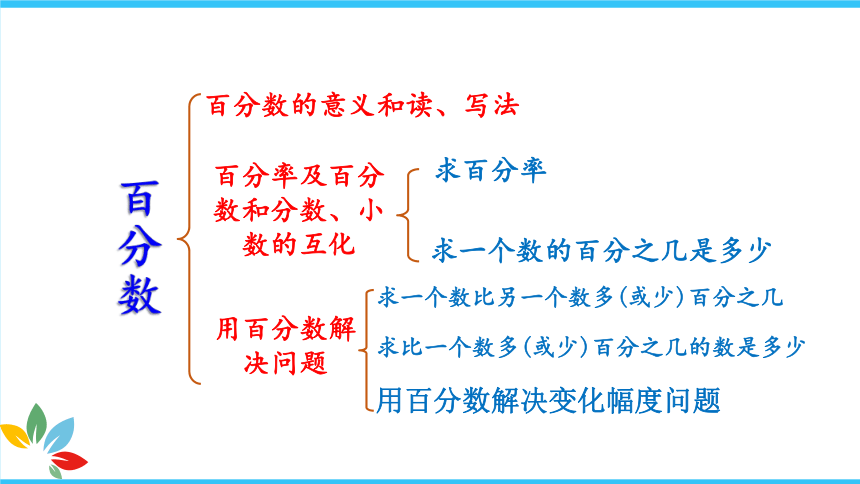
百分数
百分数的意义和读、写法
求百分率
求一个数的百分之几是多少
百分率及百分数和分数、小数的互化
用百分数解决问题
求一个数比另一个数多(或少)百分之几
用百分数解决变化幅度问题
百分数
百分数的意义和读、写法
读 法
意义:
表示一个数是另一个数的百分之几。
百分数通常不写成分数形式,而在原来分子后面加上百分号“%”来表示,读作“百分之……”。
百分数只能表示两个量之间的关系,不能表示一个具体量。
写 法
写百分数时,先写分子,再在原来的分子后面加上百分号“%”,共同组成百分数。
百分数是指的两个数的比,因此也叫百分率或百分比。
我国是一个干旱缺水严重的国家。虽然我国的淡水资源总量为27 000亿立方米,占全球水资源的6%,名列世界第六位,但是我国拥有十三亿人口,人均淡水资源低于世界平均。
6%
表示我国淡水资源占全球水资源的6%
读作“百分之六”。
02
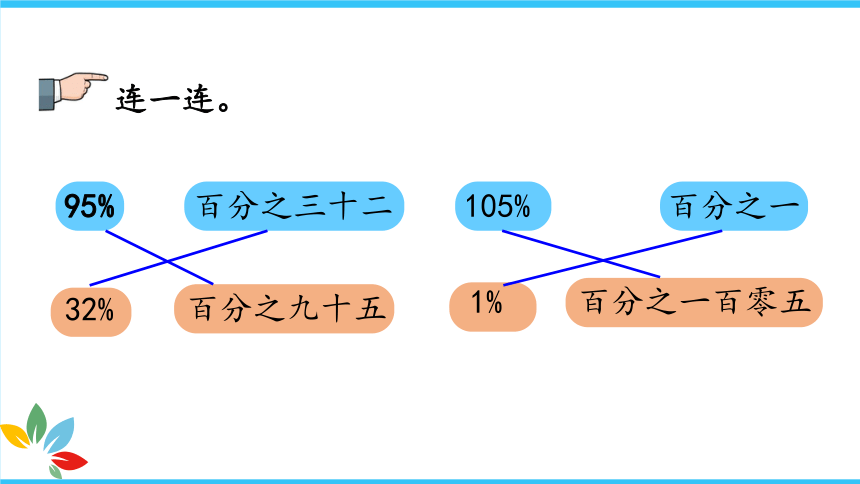
连一连。
95%
百分之三十二
105%
百分之一
百分之九十五
32%
百分之一百零五
1%
一、回顾整理
百分数与分数的关系
意 义 分 子 应用范围
百分数
分 数
只表示两个数的比的关系,不能带单位名称。
既可以表示一个具体的数,又可以表示两个数的比的关系,表示具体数时可以带单位名称。
可以是整数,也可以是小数
不能是小数,只能是除0外的自然数
在生产和生活中,常用于调查、统计、分析和比较。
常常在计算、测量中得不到整数结果时使用。
1.下面哪几个分数可以用百分数来表示 哪几个不能 说说为什么。
(1)一堆沙 t,运走了它的 。
(2) kg相当于 kg的 。
分数既可以表示具体的数量,又可以表示两个数的关系。百分数只能表示两个数的关系。
2.判断题。
(1)分母是100的分数一定是百分数。 ( )
(2)百分数只表示两个同类量之间的倍数关系。 ( )
(3)百分数与分数的意义完全相同。 ( )
(4)最大的百分数是100%。 ( )
×
√
×
×
一、回顾整理
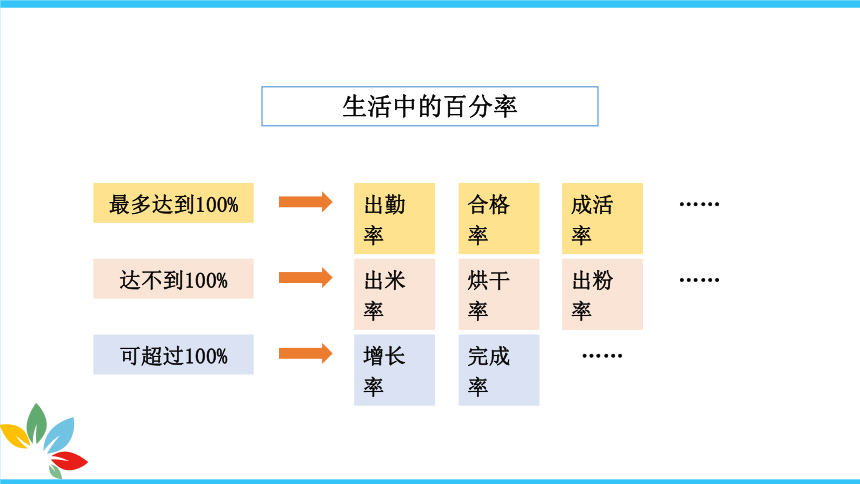
生活中的百分率
最多达到100%
出勤率
合格率
成活率
……
达不到100%
出米率
烘干率
出粉率
……
可超过100%
增长率
完成率
……
百分率
出勤率=出勤人数÷总人数×100%
发芽率=发芽数÷种植总数×100%
成活率=成活数÷种植总数×100%
……
这些百分数都不能超过100%。
百分率
六年级有学生160人,已达到国家体育锻炼标准的有140人。六年级学生的体育达标率是多少?
达标率=
体育达标的人数
六年级总人数
×100%
×100%
140
160
=0.875×100%
=87.5%
答:六年级学生的体育达标率是87.5%。
榨油厂的李伯伯告诉小芳:“500kg花生仁能榨出花生油190kg。”这些花生的出油率是多少?
×100%
190
500
=0.38×100%
=38%
答:这些花生的出油率是38%。
2. 李平家用600kg稻谷碾出420kg大米,他家稻谷的出米率是多少?
分析:这是求常见的百分率的应用题。
出米率=——————×100%
大米重量
稻谷重量
420÷600×100%=70%
答:他家稻谷出米率是70%。
油菜籽的出油率为38%,要榨1140千克菜籽油需要多少千克油菜籽。
油菜籽质量=菜籽油的
质量÷出油率
出油率=
×100%
菜籽油的质量
油菜籽的质量
1140÷38%
=3000(千克)
答:要榨1140千克菜籽油需要3000千克油菜籽。
百分数
求百分率
求一个数的百分之几是多少
百分率及百分数和分数、小数的互化
百分数和分数、小数的互化
百分数
小数
分数
改为分母是100的分数,约分,化简为最简分数
改写成分母是100的分数
去掉%,小数点向左移动两位
加上%,小数点向右移动两位
分子除以分母
转化成分母是整十整百
先把分数化成小数(除不尽时,通常保留三位小数),再化成百分数
百分数、小数和分数之间的互化
把小数化成百分数,可以把小数的小数点向右移动两位,位数不够时,用“0”补足,同时在后面加上百分号。
把分数化成百分数:(1)把分数化成分母是100的分数,然后再写成百分数形式。(2)先把分数化成小数,再化成百分数。
把下面的小数和分数改成百分数。
0.93
0.09
0.004
=93%
=9%
=0.4%
=25%
=12.5%
≈16.7%
巩固练习
把下面的百分数改成小数和分数。
73%=
7%=
0.4%=
125%=
23.9%=
60%=
二、知识应用
1.把表填完整。
小数 分数 百分数
0.45
125%
17
20
0.85
1.25
9
20
5
4
45%
85%
先化成分母是100的分数,再化简。
把分数先化成分母是100的分数,写出百分数形式。
把小数点向右移动两位,再添上百分号。
把小数点向左移动两位,并去掉百分号。
注意:计算中遇到除不尽时,一般保留三位小数,也就是百分号前面保留一位小数。
0.375
37.5%
70%
0.444
44.4%
145%
0.175
填一填。
1
把分数化成百分数时,用分子除以分母,在除不尽时,要用“≈”连接,在把近似值化为百分数的时候要用“=”连接。
选择:把 化成百分数,正确的是( A )
A.
B.
C.
【错解分析】
A选项中把0.167化成百分数时是准确值。应该用“=”连接。B选项中, 无法化成有限小数,所以0.167是近似值,应该用“≈”连接,所以本题正确的解答为 C 选项。
04
易错辨析
(1)125%= =( )÷4=( )。(填小数)
(2)学校召开教师会议,出席148人,缺席12人。出席率是( )。
( )
( )
三、巩固反馈
5
填空。
4
5
1.25
92.5%
百分数
用百分数解决问题
用百分数解决问题
1.求一个数的百分之几是多少
单位“1”的量×对应百分数=百分率的对应量
二、知识应用
小明统计了自己储蓄罐里有125枚硬币,其中1元硬币的数量
占44%,5角的占20%,1角的占36%。储蓄罐里共有多少钱?
答:储蓄罐里共有72元。
单位“1”×对应百分率=对应的数量
125×44%
=55(枚)
125×20%
=25(枚)
125×36%
=45(枚)
55×1+25×0.5+45×0.1
=55+12.5+4.5
=72(元)
据统计,世界陆栖脊椎动物大约有21122种。我国陆栖脊椎动物占世界陆栖脊椎动物的9.8%,我国陆栖脊椎动物大约有多少种?
21122×9.8%≈2070(种)
答:我国陆栖脊椎动物大约有2070种。
据统计,世界陆栖脊椎动物大约有21122种。我国陆栖脊椎动物占世界陆栖脊椎动物的9.8%,我国陆栖脊椎动物大约有多少种?
21122×9.8%≈2070(种)
答:我国陆栖脊椎动物大约有2070种。
养鸡场用2400个鸡蛋孵小鸡,有3%没有孵出来,孵出来的小鸡有多少只?
2400×(1-3%)
=2400×0.97
=2328(只)
答: 孵出来的小鸡有2328只。
2
阳光小学六(1)班参加跳绳比赛的人数占全班总人数的50%,六(2)班参加跳绳比赛的人数占全班总人数的60%。两个班级参加跳绳比赛的人数相比较,( B )
A.六(1)班多
B.六(2)班多
C.一样多
D.无法确定
【错解分析】
因为两个班级参加跳绳比赛的人数所对应的标准量(单位“1”:各班的全班总人数)无法确定,所以无法确定哪个班参加跳绳比赛的人数多,故正解为 D 选项。
用百分数解决问题
1.求一个数的百分之几是多少
单位“1”的量×对应百分数=百分率的对应量
2.求一个数是另一个数的百分之几
一个数÷另一个数(单位“1”的量)×100%=百分之几
例如
方法:
用一个数除以另一个数,结果写为百分数形式。
男生有20人,女生有15人,女生人数占男生人数的百分之几?
求一个数是另一个数的百分之几
列式:15÷20=
=
=75%
答:女生人数占男生人数的75%。
杨林家七月份用水12吨,比六月份节约了3吨。节约了( )%。
20
0
李明家本月用电量是85千瓦时,比上月节约了15千瓦时,比上月节约了百分之几?
15÷(85+15)
=15÷100
=0.15
=15%
答:比上月节约了15%。
用百分数解决问题
3.求一个数比另一个数多或(或少)百分之几
多(或少)的量÷单位“1”的量=多(或少)的百分之几
2006年全国各种运输方式完成旅客运输总量200.8亿人次,而2011年达到了351.8亿人次。2011年全国各种运输方式完成旅客运输总量比2006年增加了百分之多少?
增加的百分数=增加的人次÷2006年输送旅客总量
(351.8-200.8)÷200.8=151÷200.8≈0.752=75.2%
答:输送旅客总量比2006年增加了75.2%。
用百分数解决问题
3.求一个数比另一个数多或(或少)百分之几
多(或少)的量÷单位“1”的量=多(或少)的百分之几
4.求比一个数多(或少)百分之几的数是多少
多(或少)的量+单位“1” 或单位“1”×(1±百分数)
汽车制造厂去年生产轿车1400辆,今年比去年增加了6%。今年生产轿车多少辆?
1400×(1+6%)
=1400×106%
=1484(辆)
答:今年生产轿车1484辆。
1.5×(1+20%)
=1.5×1.2
=1.8(元)
答:每立方米水价1.8元。
某市居民用水价格提价前每立方米水价1.5元,用水价格提高20%后,每立方米水价多少元?
3231×(1-74%)
=3231×0.26
≈840(种)
答:我国的淡水鱼类大约有840种。
我国的海洋鱼类大约有3231种,我国的淡水鱼比海洋鱼类少74%。我国的淡水鱼类大约有多少种?
0
某班有男生30人,男生比女生多20%。女生有多少人?
30÷(1+20%)
=30÷1.2
=25(人)
答:女生有25人。
2011年年末全国私人汽车保有量是7872万辆,比2010年年末增长20.4 %。2010年年末全国私人汽车保有量大约是多少万辆? (得数保留整数。)
7872÷(1+20.4%)=7872÷120.4%≈6538(万辆)
答:2010年年末全国私人汽车保有量大约是6538万辆。
2011年私人汽车保有量=2010年私人汽车保有量×(1+20.4%)
2010年私人汽车保有量=2011年私人汽车保有量÷(1+20.4%)
5.已知一个数量的两次增减变化幅度,即先减少(或增加)百分之几,再增加(或减少)百分之几,求最后变化幅度
可以用假设法,把单位“1”设为一个具体的数量或“1”来解答。
按1来解答时,最后的变化幅度为
“[1-1×(1-减少幅度)×(1+增加幅度)]÷1 ”
或 “[1-1×(1+增加幅度)×(1-减少幅度)]÷1”
所得的百分数。
一种电脑销售中第一次比原价3600元降低了10%,第二次又降低了10%。这种电脑现价多少元?
3600×(1-10%)×(1-10%)
=3600×90%×90%
=2916(元)
答:这种电脑现价2916 元。
0
一种家用冰箱6月份的价格是3600元,7月份的价格比6月份降低了10%,8月份的价格又比7月份增长了10%这种冰箱8月份的价格是多少元
7月:3600×(1-10%)=3240(元)
答:这种冰箱8月份的价格是3564元。
8月:3240×(1+10%)=3564(元)
八月初猪肉价格比七月初上涨了10%,十月又比八月回落了12%,十月初主人价格比七月初涨了还是跌了?涨跌幅度是多少?
1×(1+10%) ×(1-12%)=0.968
(1-0.968)÷1=0.032=3.2%
答:十月初猪肉价格比七月初跌了,跌了3.2%。
3
一种商品,先提价10%,再降价10%,此商品的现价和原价相同。 ( √ )
【错解分析】
此商品的原价是单位“1”的量,假设原价是1,则
提价后的价格为1×(1+10%)=1.1;
降价后的价格为1.1×(1-10%)=0.99。
因为0.99<1,所以此商品的现价低于原价。
4
一种商品连续两次提价10%,现价比原价增加( A )
A.20 B.19 C.21
【错解分析】
此商品的原价是单位“1”的量,假设原价是1,则连续两次提价后的价格为1×(1+10%)×(1+10%)=1.21; 比原价增加的百分比为(1.21-1)÷1=0.21=21%,故A选项错误,正解为C选项。
本单元结束了,你有什么收获?
1.百分数可以反映现实生活中的许多社会信息,非常有用。
2.我会把解决分数实际问题的方法迁移到百分数实际问题中来。
04
畅所欲言
整理和复习
6 百分数(一)
6 百分数(一)
本单元你学习了哪些百分数的知识?这些知识对你来说是完全陌生的吗?
01
单元小结
其实,百分数是一种特殊的分数,在解决实际问题时可以联系分数的实际问题进行思考。
百分数只能表示两个量之间的关系,不能表示一个具体量。
生活中有许多百分数的应用,有的百分数可以超过100%,有的超不过,如发芽率。
求比一个数多(或少)百分之几的数是多少
百分数
百分数的意义和读、写法
求百分率
求一个数的百分之几是多少
百分率及百分数和分数、小数的互化
用百分数解决问题
求一个数比另一个数多(或少)百分之几
用百分数解决变化幅度问题
百分数
百分数的意义和读、写法
读 法
意义:
表示一个数是另一个数的百分之几。
百分数通常不写成分数形式,而在原来分子后面加上百分号“%”来表示,读作“百分之……”。
百分数只能表示两个量之间的关系,不能表示一个具体量。
写 法
写百分数时,先写分子,再在原来的分子后面加上百分号“%”,共同组成百分数。
百分数是指的两个数的比,因此也叫百分率或百分比。
我国是一个干旱缺水严重的国家。虽然我国的淡水资源总量为27 000亿立方米,占全球水资源的6%,名列世界第六位,但是我国拥有十三亿人口,人均淡水资源低于世界平均。
6%
表示我国淡水资源占全球水资源的6%
读作“百分之六”。
02
连一连。
95%
百分之三十二
105%
百分之一
百分之九十五
32%
百分之一百零五
1%
一、回顾整理
百分数与分数的关系
意 义 分 子 应用范围
百分数
分 数
只表示两个数的比的关系,不能带单位名称。
既可以表示一个具体的数,又可以表示两个数的比的关系,表示具体数时可以带单位名称。
可以是整数,也可以是小数
不能是小数,只能是除0外的自然数
在生产和生活中,常用于调查、统计、分析和比较。
常常在计算、测量中得不到整数结果时使用。
1.下面哪几个分数可以用百分数来表示 哪几个不能 说说为什么。
(1)一堆沙 t,运走了它的 。
(2) kg相当于 kg的 。
分数既可以表示具体的数量,又可以表示两个数的关系。百分数只能表示两个数的关系。
2.判断题。
(1)分母是100的分数一定是百分数。 ( )
(2)百分数只表示两个同类量之间的倍数关系。 ( )
(3)百分数与分数的意义完全相同。 ( )
(4)最大的百分数是100%。 ( )
×
√
×
×
一、回顾整理
生活中的百分率
最多达到100%
出勤率
合格率
成活率
……
达不到100%
出米率
烘干率
出粉率
……
可超过100%
增长率
完成率
……
百分率
出勤率=出勤人数÷总人数×100%
发芽率=发芽数÷种植总数×100%
成活率=成活数÷种植总数×100%
……
这些百分数都不能超过100%。
百分率
六年级有学生160人,已达到国家体育锻炼标准的有140人。六年级学生的体育达标率是多少?
达标率=
体育达标的人数
六年级总人数
×100%
×100%
140
160
=0.875×100%
=87.5%
答:六年级学生的体育达标率是87.5%。
榨油厂的李伯伯告诉小芳:“500kg花生仁能榨出花生油190kg。”这些花生的出油率是多少?
×100%
190
500
=0.38×100%
=38%
答:这些花生的出油率是38%。
2. 李平家用600kg稻谷碾出420kg大米,他家稻谷的出米率是多少?
分析:这是求常见的百分率的应用题。
出米率=——————×100%
大米重量
稻谷重量
420÷600×100%=70%
答:他家稻谷出米率是70%。
油菜籽的出油率为38%,要榨1140千克菜籽油需要多少千克油菜籽。
油菜籽质量=菜籽油的
质量÷出油率
出油率=
×100%
菜籽油的质量
油菜籽的质量
1140÷38%
=3000(千克)
答:要榨1140千克菜籽油需要3000千克油菜籽。
百分数
求百分率
求一个数的百分之几是多少
百分率及百分数和分数、小数的互化
百分数和分数、小数的互化
百分数
小数
分数
改为分母是100的分数,约分,化简为最简分数
改写成分母是100的分数
去掉%,小数点向左移动两位
加上%,小数点向右移动两位
分子除以分母
转化成分母是整十整百
先把分数化成小数(除不尽时,通常保留三位小数),再化成百分数
百分数、小数和分数之间的互化
把小数化成百分数,可以把小数的小数点向右移动两位,位数不够时,用“0”补足,同时在后面加上百分号。
把分数化成百分数:(1)把分数化成分母是100的分数,然后再写成百分数形式。(2)先把分数化成小数,再化成百分数。
把下面的小数和分数改成百分数。
0.93
0.09
0.004
=93%
=9%
=0.4%
=25%
=12.5%
≈16.7%
巩固练习
把下面的百分数改成小数和分数。
73%=
7%=
0.4%=
125%=
23.9%=
60%=
二、知识应用
1.把表填完整。
小数 分数 百分数
0.45
125%
17
20
0.85
1.25
9
20
5
4
45%
85%
先化成分母是100的分数,再化简。
把分数先化成分母是100的分数,写出百分数形式。
把小数点向右移动两位,再添上百分号。
把小数点向左移动两位,并去掉百分号。
注意:计算中遇到除不尽时,一般保留三位小数,也就是百分号前面保留一位小数。
0.375
37.5%
70%
0.444
44.4%
145%
0.175
填一填。
1
把分数化成百分数时,用分子除以分母,在除不尽时,要用“≈”连接,在把近似值化为百分数的时候要用“=”连接。
选择:把 化成百分数,正确的是( A )
A.
B.
C.
【错解分析】
A选项中把0.167化成百分数时是准确值。应该用“=”连接。B选项中, 无法化成有限小数,所以0.167是近似值,应该用“≈”连接,所以本题正确的解答为 C 选项。
04
易错辨析
(1)125%= =( )÷4=( )。(填小数)
(2)学校召开教师会议,出席148人,缺席12人。出席率是( )。
( )
( )
三、巩固反馈
5
填空。
4
5
1.25
92.5%
百分数
用百分数解决问题
用百分数解决问题
1.求一个数的百分之几是多少
单位“1”的量×对应百分数=百分率的对应量
二、知识应用
小明统计了自己储蓄罐里有125枚硬币,其中1元硬币的数量
占44%,5角的占20%,1角的占36%。储蓄罐里共有多少钱?
答:储蓄罐里共有72元。
单位“1”×对应百分率=对应的数量
125×44%
=55(枚)
125×20%
=25(枚)
125×36%
=45(枚)
55×1+25×0.5+45×0.1
=55+12.5+4.5
=72(元)
据统计,世界陆栖脊椎动物大约有21122种。我国陆栖脊椎动物占世界陆栖脊椎动物的9.8%,我国陆栖脊椎动物大约有多少种?
21122×9.8%≈2070(种)
答:我国陆栖脊椎动物大约有2070种。
据统计,世界陆栖脊椎动物大约有21122种。我国陆栖脊椎动物占世界陆栖脊椎动物的9.8%,我国陆栖脊椎动物大约有多少种?
21122×9.8%≈2070(种)
答:我国陆栖脊椎动物大约有2070种。
养鸡场用2400个鸡蛋孵小鸡,有3%没有孵出来,孵出来的小鸡有多少只?
2400×(1-3%)
=2400×0.97
=2328(只)
答: 孵出来的小鸡有2328只。
2
阳光小学六(1)班参加跳绳比赛的人数占全班总人数的50%,六(2)班参加跳绳比赛的人数占全班总人数的60%。两个班级参加跳绳比赛的人数相比较,( B )
A.六(1)班多
B.六(2)班多
C.一样多
D.无法确定
【错解分析】
因为两个班级参加跳绳比赛的人数所对应的标准量(单位“1”:各班的全班总人数)无法确定,所以无法确定哪个班参加跳绳比赛的人数多,故正解为 D 选项。
用百分数解决问题
1.求一个数的百分之几是多少
单位“1”的量×对应百分数=百分率的对应量
2.求一个数是另一个数的百分之几
一个数÷另一个数(单位“1”的量)×100%=百分之几
例如
方法:
用一个数除以另一个数,结果写为百分数形式。
男生有20人,女生有15人,女生人数占男生人数的百分之几?
求一个数是另一个数的百分之几
列式:15÷20=
=
=75%
答:女生人数占男生人数的75%。
杨林家七月份用水12吨,比六月份节约了3吨。节约了( )%。
20
0
李明家本月用电量是85千瓦时,比上月节约了15千瓦时,比上月节约了百分之几?
15÷(85+15)
=15÷100
=0.15
=15%
答:比上月节约了15%。
用百分数解决问题
3.求一个数比另一个数多或(或少)百分之几
多(或少)的量÷单位“1”的量=多(或少)的百分之几
2006年全国各种运输方式完成旅客运输总量200.8亿人次,而2011年达到了351.8亿人次。2011年全国各种运输方式完成旅客运输总量比2006年增加了百分之多少?
增加的百分数=增加的人次÷2006年输送旅客总量
(351.8-200.8)÷200.8=151÷200.8≈0.752=75.2%
答:输送旅客总量比2006年增加了75.2%。
用百分数解决问题
3.求一个数比另一个数多或(或少)百分之几
多(或少)的量÷单位“1”的量=多(或少)的百分之几
4.求比一个数多(或少)百分之几的数是多少
多(或少)的量+单位“1” 或单位“1”×(1±百分数)
汽车制造厂去年生产轿车1400辆,今年比去年增加了6%。今年生产轿车多少辆?
1400×(1+6%)
=1400×106%
=1484(辆)
答:今年生产轿车1484辆。
1.5×(1+20%)
=1.5×1.2
=1.8(元)
答:每立方米水价1.8元。
某市居民用水价格提价前每立方米水价1.5元,用水价格提高20%后,每立方米水价多少元?
3231×(1-74%)
=3231×0.26
≈840(种)
答:我国的淡水鱼类大约有840种。
我国的海洋鱼类大约有3231种,我国的淡水鱼比海洋鱼类少74%。我国的淡水鱼类大约有多少种?
0
某班有男生30人,男生比女生多20%。女生有多少人?
30÷(1+20%)
=30÷1.2
=25(人)
答:女生有25人。
2011年年末全国私人汽车保有量是7872万辆,比2010年年末增长20.4 %。2010年年末全国私人汽车保有量大约是多少万辆? (得数保留整数。)
7872÷(1+20.4%)=7872÷120.4%≈6538(万辆)
答:2010年年末全国私人汽车保有量大约是6538万辆。
2011年私人汽车保有量=2010年私人汽车保有量×(1+20.4%)
2010年私人汽车保有量=2011年私人汽车保有量÷(1+20.4%)
5.已知一个数量的两次增减变化幅度,即先减少(或增加)百分之几,再增加(或减少)百分之几,求最后变化幅度
可以用假设法,把单位“1”设为一个具体的数量或“1”来解答。
按1来解答时,最后的变化幅度为
“[1-1×(1-减少幅度)×(1+增加幅度)]÷1 ”
或 “[1-1×(1+增加幅度)×(1-减少幅度)]÷1”
所得的百分数。
一种电脑销售中第一次比原价3600元降低了10%,第二次又降低了10%。这种电脑现价多少元?
3600×(1-10%)×(1-10%)
=3600×90%×90%
=2916(元)
答:这种电脑现价2916 元。
0
一种家用冰箱6月份的价格是3600元,7月份的价格比6月份降低了10%,8月份的价格又比7月份增长了10%这种冰箱8月份的价格是多少元
7月:3600×(1-10%)=3240(元)
答:这种冰箱8月份的价格是3564元。
8月:3240×(1+10%)=3564(元)
八月初猪肉价格比七月初上涨了10%,十月又比八月回落了12%,十月初主人价格比七月初涨了还是跌了?涨跌幅度是多少?
1×(1+10%) ×(1-12%)=0.968
(1-0.968)÷1=0.032=3.2%
答:十月初猪肉价格比七月初跌了,跌了3.2%。
3
一种商品,先提价10%,再降价10%,此商品的现价和原价相同。 ( √ )
【错解分析】
此商品的原价是单位“1”的量,假设原价是1,则
提价后的价格为1×(1+10%)=1.1;
降价后的价格为1.1×(1-10%)=0.99。
因为0.99<1,所以此商品的现价低于原价。
4
一种商品连续两次提价10%,现价比原价增加( A )
A.20 B.19 C.21
【错解分析】
此商品的原价是单位“1”的量,假设原价是1,则连续两次提价后的价格为1×(1+10%)×(1+10%)=1.21; 比原价增加的百分比为(1.21-1)÷1=0.21=21%,故A选项错误,正解为C选项。
本单元结束了,你有什么收获?
1.百分数可以反映现实生活中的许多社会信息,非常有用。
2.我会把解决分数实际问题的方法迁移到百分数实际问题中来。
04
畅所欲言
