5.2运动的合成与分解同步练习(word版含答案)
文档属性
| 名称 | 5.2运动的合成与分解同步练习(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 365.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-12-02 22:33:20 | ||
图片预览




文档简介
5.2运动的合成与分解
一、选择题
1.河宽为d=100m,水流速度v1=3m/s,船在静水中运动速度v2=4m/s,设船最短过河时间为t,最短过河位移为s,则( )
A.t=50s,s=125m B.t=25s,s=125m
C.t=25s,s=100m D.t=41.5s,s=100m
2.光滑半球A放在竖直面光滑的墙角,并用手推着保持静止。现在A与墙壁之间放入光滑球B,放手让A和B由静止开始运动,当A、B运动到图示位置时,二者球心的连线与水平面成θ角,速度大小分别为和,则以下关系正确的是
A. B.
C. D.
3.小船在静水中的速度为3m/s,它在一条流速为4m/s,河宽为150m的河流中渡河,则
A.小船不可能垂直河岸到达对岸
B.小船渡河的时间可能为40s
C.小船渡河时间可能为30s
D.小船若在50s内渡河,到达河对岸时被冲下150m远
4.在宽度为d的河中,水流速度为v2,船在静水中速度为v1(且v1>v2),方向可以选择,现让该船开始渡河,则下列说法错误的是( )
A.最短渡河时间为
B.最短渡河位移为d
C.只有当船头垂直河岸渡河时,渡河时间才和水速无关
D.不管船头与河岸夹角是多少,渡河时间和水速均无关
5.如图所示,固定的竖直光滑细杆上穿有一小球,长度不可伸长的轻绳跨过定滑轮后一端与小球相连,以恒定的速率沿绳拉动轻绳的另一端,使小球沿细杆向上运动,当小球上升到某高度时,连接小球的轻绳与细杆的夹角为(),此时小球沿细杆上升的速度大小为,则下列说法正确的是( )
A. B.
C.此时小球处于超重状态 D.此时小球处于失重状态
6.下列说法中正确的是( )
A.任何曲线运动都是变加速运动
B.两个匀速直线运动(速率不等)的合运动一定是匀速直线运动
C.两个匀加速直线运动的合运动一定不是直线运动
D.一个匀速直线运动和一个匀加速直线运动的合运动一定是曲线运动
7.一个质量的质点,从水平面内的直角坐标系的原点出发开始运动,该质点沿方向受如图甲所示的力的作用,沿轴正方向的图像如图乙所示,那么质点到达如图丙所示点( )
A.所用时间为 B.速度大小为
C.发生的位移大小为 D.总路程为
8.下列说法正确的是
A.两匀速直线运动的合运动的轨迹必是直线
B.两匀变速直线运动的合运动的轨迹必是直线
C.一个匀变速直线运动和一个匀速直线运动的合运动的轨迹一定是曲线
D.两个初速度为0的匀变速直线运动的合运动的轨迹一定是曲线
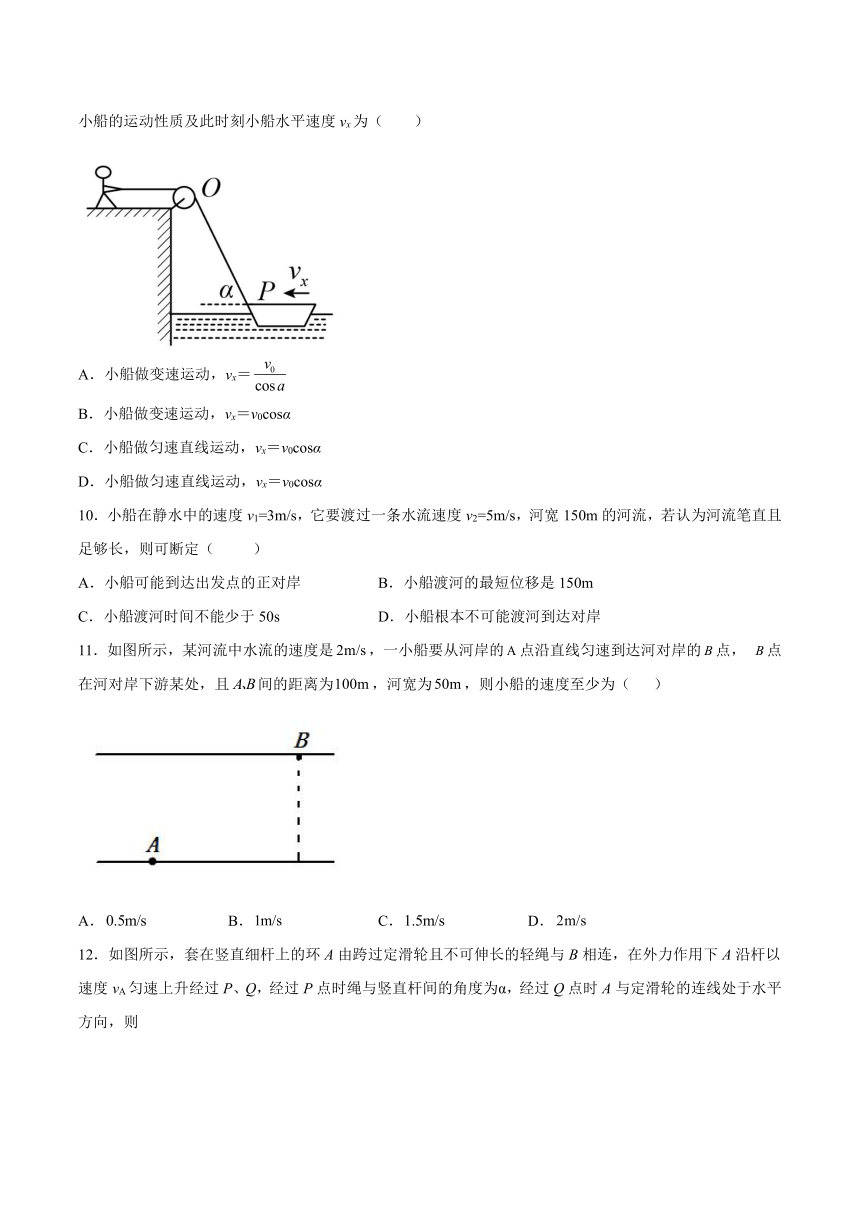
9.如图所示,某人用绳通过定滑轮拉小船,设人匀速拉绳的速度为v0,绳某时刻与水平方向夹角为α,则小船的运动性质及此时刻小船水平速度vx为( )
A.小船做变速运动,vx=
B.小船做变速运动,vx=v0cosα
C.小船做匀速直线运动,vx=v0cosα
D.小船做匀速直线运动,vx=v0cosα
10.小船在静水中的速度v1=3m/s,它要渡过一条水流速度v2=5m/s,河宽150m的河流,若认为河流笔直且足够长,则可断定( )
A.小船可能到达出发点的正对岸 B.小船渡河的最短位移是150m
C.小船渡河时间不能少于50s D.小船根本不可能渡河到达对岸
11.如图所示,某河流中水流的速度是,一小船要从河岸的点沿直线匀速到达河对岸的点, 点在河对岸下游某处,且间的距离为,河宽为,则小船的速度至少为( )
A. B. C. D.
12.如图所示,套在竖直细杆上的环A由跨过定滑轮且不可伸长的轻绳与B相连,在外力作用下A沿杆以速度vA匀速上升经过P、Q,经过P点时绳与竖直杆间的角度为α,经过Q点时A与定滑轮的连线处于水平方向,则
A.经过Q点时,B的速度方向向下
B.经过P点时,B的速度等于
C.当A从P至Q的过程中,B处于失重状态
D.当A从P至Q的过程中,B受到的拉力大于重力
13.如图所示,战斗机离舰执行任务,若战斗机离开甲板时的水平分速度为40m/s,竖直分速度为20m/s,已知飞机在水平方向做加速度大小等于的匀加速直线运动,在竖直方向做加速度大小等于的匀加速直线运动。则离舰后( )
A.飞机的运动轨迹为曲线
B.10s内飞机水平方向的分位移是竖直方向的分位移大小的2倍
C.10s末飞机的速度方向与水平方向夹角为
D.飞机在20s内水平方向的平均速度为50m/s/
14.如图所示,在河岸上通过轮轴(轮套在有一定大小的轴上,轮与轴绕共同的中轴一起转动)用细绳拉船,轮与轴的半径比 .轮上细绳的速度恒为,当轴上细绳拉船的部分与水平方向成60°角时,船的速度是( )
A.2m/s B.4 m/s C.8m/s D.16 m/s
15.如图,在灭火抢险的过程中,消防队员有时要借助消防车上的梯子爬到高处进行救人或灭火作业.为了节省救援时间,消防车向前前进的过程中,人相对梯子匀加速向上运动,在地面上看消防队员的运动,下列说法中正确的是( )
A.当消防车匀速前进时,消防队员可能做匀加速直线运动
B.当消防车匀速前进时,消防队员水平方向的速度保持不变
C.当消防车匀加速前进时,消防队员一定做匀变速曲线运动
D.当消防车匀减速前进时,消防队员一定做匀变速曲线运动
二、综合题
16.河宽420m,船在静水中的速度是5m/s,水流速度是4m/s,则渡河的最短时间是________,以最短位移渡河的时间是________。
17.小船在200m宽的河流中横渡,水流速度为3m/s,船在静水中的航速是5m/s,要使小船渡河的航程最短,最短的航程是________m;这样渡河到达对岸的时间是_________s。
18.某次抗洪抢险中,必须用小船将物资送至河流对岸。如图所示,处的下游靠河岸处是个旋涡,点和旋涡的连线与河岸的最大夹角为30°,若河流中水流的速度大小恒为,为使小船从点以恒定的速度安全到达对岸,则小船在静水冲航行时速度的最小值为______,此时小船航行的实际速度大小为______。
19.一物体在光滑水平面上运动,它的x方向和y方向的两个运动的速度—时间图象如图所示。
(1)判断物体的运动性质;
(2)计算物体的初速度;
(3)计算物体在前3s内和前6s内的位移。
20.河宽d=200 m,水流速度v1=3 m/s,船在静水中的速度v2=5 m/s。求:
(1)欲使船渡河时间最短,船应怎样渡河?最短时间是多少?船经过的位移多大?
(2)欲使船航行距离最短,船应怎样渡河?渡河时间多长?
21.如图所示,一小船正在渡河,在离对岸30m处,发现其下游40m处有一危险水域,若水流速度为5m/s,为了使小船在进入危险水域之前到达对岸,那么小船从现在起相对于静水的最小速度应为多大?此时船头的航向如何?渡河要用多少时间?
参考答案
1.C
【详解】
当以静水中的速度垂直河岸过河的时候渡河时间最短,则知
小船以最短位移过河时,则静水中的速度斜着向上游,合速度垂直河岸,最短位移s等于河宽d,故C正确,ABD错误。
故选C。
2.D
【详解】
将A、B两球的速度沿两球心的连线和垂直两球心连线分解,如图,由关联速度的关系可得
解得
故D正确。
故选D。
3.A
【详解】
由题意知,水流的速度大于船在静水中的速度,所以小船不可能垂直河岸到达对岸,故A正确;当船头垂直河岸时,渡河时间最短为,所以B错误;C错误;平行与河岸的位移x=vt=200m,所以D错误.
4.C
【详解】
A.当船头与河岸垂直时,渡河时间最短,最短时间为:
故A不符合题意;
B.由于v1>v2,合速度方向可以垂直河岸,所以最短渡河位移大小为d,故B不符题意;
CD.渡河时间取决于v1在垂直河岸方向的分量,无论什么情况水速都与渡河时间无关,故C符合题意,D不符合题意;
本题选择错误的,故选C。
5.C
【详解】
AB.小球上升的速度沿绳方向的分量与拉动绳子的速度相等,则
故选项A、B错误;
CD.上升的过程中,变大,大小不变,变大,小球在加速上升,处于超重状态,故选项C正确,选项D错误。
故选C。
6.B
【详解】
A.曲线运动不一定都是变加速运动,也可能是匀加速运动,例如平抛运动,A错误;
B.两个匀速直线运动(速率不等)的合运动一定是匀速直线运动,B正确;
C.两个匀加速直线运动的合运动,如果两个合初速度和合加速度共线,则仍然是直线运动,C错误;
D.一个匀速直线运动和一个匀加速直线运动的合运动不一定是曲线运动,例如竖直上抛运动,D错误。
故选B。
7.A
【详解】
A.质点在y方向做匀速运动,则所用时间为
A正确;
B.质点在x方向做匀加速运动则到达A点时沿x方向
解得
vx=6m/s
则合速度大小为
B错误;
C.发生的位移大小为
C错误;
D.物体做曲线运动,则总路程大于,D错误。
故选A。
8.A
【详解】
匀速直线运动受到的合外力等于零,所以两个匀速直线运动的合运动一定还是匀速直线运动,故A正确;两匀变速直线运动合成,合速度的方向与合加速度的方向不一定在同一条直线上,轨迹不一定是直线,故B错误;若匀变速直线运动与匀速直线运动两个运动在同一条直线上,合运动为直线,故C错误;初速度为零的匀变速直线运动,合速度为零,合加速度恒定,合运动做匀变速直线运动,故D错误.所以A正确,BCD错误.
9.A
【详解】
小船的实际运动是水平向左的运动,它的速度vx可以产生两个效果:一是使绳子OP段缩短;二是使OP段绳与竖直方向的夹角减小.所以小船的速度vx应有沿OP绳指向O的分速度v0和垂直OP的分速度v1,由运动的分解可求得
α角逐渐变大,可得vx是逐渐变大的,所以小船做的是变速运动。
故选A。
10.C
【详解】
A. 因为静水中速度的大小小于水流速度的大小,则合速度的方向不可能垂直河岸,所以小船不可能到达正对岸.故A错误,B错误;
C. 当小船在静水速与河岸垂直时,渡河的时间最短,则最短时间t=d/v静=150/3s=50s.故C正确;
D. 将小船的速度沿河岸和垂直河岸分解,只要小船有垂直河岸方向的分量,就能到达河对岸,故D错误;
故选C
11.B
【详解】
要使小船避开危险区沿直线到达对岸,则有合运动的最大位移为100m.因此已知小船能安全到达河岸的合速度,设此速度与水流速度的夹角为θ,即有:sinθ=,所以θ=30°;又已知流水速度,则可得小船在静水中最小速度为:v船=v水sinθ=×2m/s=1m/s故选B.
12.D
【详解】
对于A,它的速度如图中标出的vA,这个速度看成是A的合速度,其分速度分别是va,vb,
其中va就是B的速度vB(同一根绳子,大小相同),刚开始时B的速度为vB=vAcosα;当A环上升至与定滑轮的连线处于水平位置时,va=0,所以B的速度vB=0,故AB错误;因A匀速上升时,由公式vB=vAcosα,当A上升时,夹角α增大,因此B做向下减速运动,则处于超重状态,由牛顿第二定律,可知绳对B的拉力大于B的重力,故C错误、D正确;
13.B
【详解】
A.飞机起飞后的合速度与合加速度方向一致,所以飞机运动轨迹为直线,A错误;
B.10s内水平方向位移
竖直方向位移
B正确;
C.飞机飞行方向与水平方向夹角的正切,C错误;
D.飞机在20s内水平方向的位移
则平均速度为
D错误。
故选B。
14.B
【详解】
轮与轴同轴转动,角速度相同,所以根据公式可得,船的速度速度可分解为轴上细绳的速度和垂直绳子斜向下的速度,根据几何知识可得,故B正确;
15.D
【解析】
消防员参与了沿梯子方向的匀加速直线运动和水平方向上的匀速直线运动,通过合速度与合加速度是否在同一条直线上判断消防员做直线运动还是曲线运动.若消防车匀速前进,根据运动的合成,知合速度的方向与加速度的方向不在同一条直线,其加速度的方向大小不变,所以消防员做匀变速曲线运动,故A错误
将消防员的运动分解为水平方向和竖直方向,知水平方向上的最终的速度为匀速后退的速度和沿梯子方向速度在水平方向上的分速度的合速度,因为沿梯子方向的速度在水平方向上的分速度在变,所以消防队员水平方向的速度在变.故B错误
若消防车匀加速前进,根据运动的合成,知合速度的方向与合加速度的方向有可能在同一条直线,其加速度的方向大小不变,所以消防员有可能做匀变速直线运动,故C错误
若消防车匀减速前进,根据运动的合成,知合速度的方向与合加速度的方向不在同一条直线,其加速度的方向大小不变,所以消防员做匀变速曲线运动,故D正确
16.84s 140s
【详解】
[1]当船头垂直河岸渡河时,渡河时间最短
[2] 小船以最短距离过河时,则静水中的速度斜着向上游,合速度垂直河岸,则由矢量合成的平行四边形法则,那么船垂直河岸行驶的速度为
渡河最小位移是420m,所以渡河时间为
17.200m 50s
【详解】
[1][2]因为船速大于水速,故合速度可以垂直河岸,则最短航程为河宽200m。根据几何关系可知此时船的合速度
则最短航程渡河时间
18.1
【详解】
[1][2]如图所示,当小船在静水中的速度与其在河流中的速度垂直时,小船在静水中的速度最小,且最小值
此时小船航行的实际速度大小
19.(1) 匀变速曲线运动;(2),方向与x轴成53°;(3)108.2m,方向与x轴成;180m,方向沿x轴。
【详解】
(1) 由图可看出,物体沿x方向的分运动为匀速直线运动,沿y方向的分运动为匀变速直线运动,故合运动为匀变速曲线运动。
(2) 物体的初速度
方向与x轴成53°
(3) 在前3s内
,
故
方向与x轴成。
在前6s内
sx′=vxt′=30×6m=180m,sy′=0
故
s′=sx′=180m
方向沿x轴。
20.(1)船头指向对岸,40s,233 m;(2)航行速度v2与岸成53°,50s
【详解】
(1)当船头指向对岸时,渡河时间最短,如图甲所示
最短渡河时间
船经过的位移大小
(2)欲使船航行距离最短,需使船的实际位移(合位移)与河岸垂直,设此时船的航行速度v2与岸成角,如图乙所示。则
故航行速度v2与岸成53°;船航行的实际速度为
渡河时间
21.3m/s,方向斜向上游河岸,且与河岸成53°角,12.5s
【详解】
小船到达危险水域前,恰好到达对岸,如图所示
设合位移s的方向与河岸成θ角,则
故
小船的合速度方向与合位移方向相同,由平行四边形定则可知,只有当小船相对于静水的速度与合速度方向垂直时,小船相对于静水的速度最小。由图知,此最小速度为
其方向斜向上游河岸,且与河岸成53°角。
合速度为
合位移为
渡河所用时间为
一、选择题
1.河宽为d=100m,水流速度v1=3m/s,船在静水中运动速度v2=4m/s,设船最短过河时间为t,最短过河位移为s,则( )
A.t=50s,s=125m B.t=25s,s=125m
C.t=25s,s=100m D.t=41.5s,s=100m
2.光滑半球A放在竖直面光滑的墙角,并用手推着保持静止。现在A与墙壁之间放入光滑球B,放手让A和B由静止开始运动,当A、B运动到图示位置时,二者球心的连线与水平面成θ角,速度大小分别为和,则以下关系正确的是
A. B.
C. D.
3.小船在静水中的速度为3m/s,它在一条流速为4m/s,河宽为150m的河流中渡河,则
A.小船不可能垂直河岸到达对岸
B.小船渡河的时间可能为40s
C.小船渡河时间可能为30s
D.小船若在50s内渡河,到达河对岸时被冲下150m远
4.在宽度为d的河中,水流速度为v2,船在静水中速度为v1(且v1>v2),方向可以选择,现让该船开始渡河,则下列说法错误的是( )
A.最短渡河时间为
B.最短渡河位移为d
C.只有当船头垂直河岸渡河时,渡河时间才和水速无关
D.不管船头与河岸夹角是多少,渡河时间和水速均无关
5.如图所示,固定的竖直光滑细杆上穿有一小球,长度不可伸长的轻绳跨过定滑轮后一端与小球相连,以恒定的速率沿绳拉动轻绳的另一端,使小球沿细杆向上运动,当小球上升到某高度时,连接小球的轻绳与细杆的夹角为(),此时小球沿细杆上升的速度大小为,则下列说法正确的是( )
A. B.
C.此时小球处于超重状态 D.此时小球处于失重状态
6.下列说法中正确的是( )
A.任何曲线运动都是变加速运动
B.两个匀速直线运动(速率不等)的合运动一定是匀速直线运动
C.两个匀加速直线运动的合运动一定不是直线运动
D.一个匀速直线运动和一个匀加速直线运动的合运动一定是曲线运动
7.一个质量的质点,从水平面内的直角坐标系的原点出发开始运动,该质点沿方向受如图甲所示的力的作用,沿轴正方向的图像如图乙所示,那么质点到达如图丙所示点( )
A.所用时间为 B.速度大小为
C.发生的位移大小为 D.总路程为
8.下列说法正确的是
A.两匀速直线运动的合运动的轨迹必是直线
B.两匀变速直线运动的合运动的轨迹必是直线
C.一个匀变速直线运动和一个匀速直线运动的合运动的轨迹一定是曲线
D.两个初速度为0的匀变速直线运动的合运动的轨迹一定是曲线
9.如图所示,某人用绳通过定滑轮拉小船,设人匀速拉绳的速度为v0,绳某时刻与水平方向夹角为α,则小船的运动性质及此时刻小船水平速度vx为( )
A.小船做变速运动,vx=
B.小船做变速运动,vx=v0cosα
C.小船做匀速直线运动,vx=v0cosα
D.小船做匀速直线运动,vx=v0cosα
10.小船在静水中的速度v1=3m/s,它要渡过一条水流速度v2=5m/s,河宽150m的河流,若认为河流笔直且足够长,则可断定( )
A.小船可能到达出发点的正对岸 B.小船渡河的最短位移是150m
C.小船渡河时间不能少于50s D.小船根本不可能渡河到达对岸
11.如图所示,某河流中水流的速度是,一小船要从河岸的点沿直线匀速到达河对岸的点, 点在河对岸下游某处,且间的距离为,河宽为,则小船的速度至少为( )
A. B. C. D.
12.如图所示,套在竖直细杆上的环A由跨过定滑轮且不可伸长的轻绳与B相连,在外力作用下A沿杆以速度vA匀速上升经过P、Q,经过P点时绳与竖直杆间的角度为α,经过Q点时A与定滑轮的连线处于水平方向,则
A.经过Q点时,B的速度方向向下
B.经过P点时,B的速度等于
C.当A从P至Q的过程中,B处于失重状态
D.当A从P至Q的过程中,B受到的拉力大于重力
13.如图所示,战斗机离舰执行任务,若战斗机离开甲板时的水平分速度为40m/s,竖直分速度为20m/s,已知飞机在水平方向做加速度大小等于的匀加速直线运动,在竖直方向做加速度大小等于的匀加速直线运动。则离舰后( )
A.飞机的运动轨迹为曲线
B.10s内飞机水平方向的分位移是竖直方向的分位移大小的2倍
C.10s末飞机的速度方向与水平方向夹角为
D.飞机在20s内水平方向的平均速度为50m/s/
14.如图所示,在河岸上通过轮轴(轮套在有一定大小的轴上,轮与轴绕共同的中轴一起转动)用细绳拉船,轮与轴的半径比 .轮上细绳的速度恒为,当轴上细绳拉船的部分与水平方向成60°角时,船的速度是( )
A.2m/s B.4 m/s C.8m/s D.16 m/s
15.如图,在灭火抢险的过程中,消防队员有时要借助消防车上的梯子爬到高处进行救人或灭火作业.为了节省救援时间,消防车向前前进的过程中,人相对梯子匀加速向上运动,在地面上看消防队员的运动,下列说法中正确的是( )
A.当消防车匀速前进时,消防队员可能做匀加速直线运动
B.当消防车匀速前进时,消防队员水平方向的速度保持不变
C.当消防车匀加速前进时,消防队员一定做匀变速曲线运动
D.当消防车匀减速前进时,消防队员一定做匀变速曲线运动
二、综合题
16.河宽420m,船在静水中的速度是5m/s,水流速度是4m/s,则渡河的最短时间是________,以最短位移渡河的时间是________。
17.小船在200m宽的河流中横渡,水流速度为3m/s,船在静水中的航速是5m/s,要使小船渡河的航程最短,最短的航程是________m;这样渡河到达对岸的时间是_________s。
18.某次抗洪抢险中,必须用小船将物资送至河流对岸。如图所示,处的下游靠河岸处是个旋涡,点和旋涡的连线与河岸的最大夹角为30°,若河流中水流的速度大小恒为,为使小船从点以恒定的速度安全到达对岸,则小船在静水冲航行时速度的最小值为______,此时小船航行的实际速度大小为______。
19.一物体在光滑水平面上运动,它的x方向和y方向的两个运动的速度—时间图象如图所示。
(1)判断物体的运动性质;
(2)计算物体的初速度;
(3)计算物体在前3s内和前6s内的位移。
20.河宽d=200 m,水流速度v1=3 m/s,船在静水中的速度v2=5 m/s。求:
(1)欲使船渡河时间最短,船应怎样渡河?最短时间是多少?船经过的位移多大?
(2)欲使船航行距离最短,船应怎样渡河?渡河时间多长?
21.如图所示,一小船正在渡河,在离对岸30m处,发现其下游40m处有一危险水域,若水流速度为5m/s,为了使小船在进入危险水域之前到达对岸,那么小船从现在起相对于静水的最小速度应为多大?此时船头的航向如何?渡河要用多少时间?
参考答案
1.C
【详解】
当以静水中的速度垂直河岸过河的时候渡河时间最短,则知
小船以最短位移过河时,则静水中的速度斜着向上游,合速度垂直河岸,最短位移s等于河宽d,故C正确,ABD错误。
故选C。
2.D
【详解】
将A、B两球的速度沿两球心的连线和垂直两球心连线分解,如图,由关联速度的关系可得
解得
故D正确。
故选D。
3.A
【详解】
由题意知,水流的速度大于船在静水中的速度,所以小船不可能垂直河岸到达对岸,故A正确;当船头垂直河岸时,渡河时间最短为,所以B错误;C错误;平行与河岸的位移x=vt=200m,所以D错误.
4.C
【详解】
A.当船头与河岸垂直时,渡河时间最短,最短时间为:
故A不符合题意;
B.由于v1>v2,合速度方向可以垂直河岸,所以最短渡河位移大小为d,故B不符题意;
CD.渡河时间取决于v1在垂直河岸方向的分量,无论什么情况水速都与渡河时间无关,故C符合题意,D不符合题意;
本题选择错误的,故选C。
5.C
【详解】
AB.小球上升的速度沿绳方向的分量与拉动绳子的速度相等,则
故选项A、B错误;
CD.上升的过程中,变大,大小不变,变大,小球在加速上升,处于超重状态,故选项C正确,选项D错误。
故选C。
6.B
【详解】
A.曲线运动不一定都是变加速运动,也可能是匀加速运动,例如平抛运动,A错误;
B.两个匀速直线运动(速率不等)的合运动一定是匀速直线运动,B正确;
C.两个匀加速直线运动的合运动,如果两个合初速度和合加速度共线,则仍然是直线运动,C错误;
D.一个匀速直线运动和一个匀加速直线运动的合运动不一定是曲线运动,例如竖直上抛运动,D错误。
故选B。
7.A
【详解】
A.质点在y方向做匀速运动,则所用时间为
A正确;
B.质点在x方向做匀加速运动则到达A点时沿x方向
解得
vx=6m/s
则合速度大小为
B错误;
C.发生的位移大小为
C错误;
D.物体做曲线运动,则总路程大于,D错误。
故选A。
8.A
【详解】
匀速直线运动受到的合外力等于零,所以两个匀速直线运动的合运动一定还是匀速直线运动,故A正确;两匀变速直线运动合成,合速度的方向与合加速度的方向不一定在同一条直线上,轨迹不一定是直线,故B错误;若匀变速直线运动与匀速直线运动两个运动在同一条直线上,合运动为直线,故C错误;初速度为零的匀变速直线运动,合速度为零,合加速度恒定,合运动做匀变速直线运动,故D错误.所以A正确,BCD错误.
9.A
【详解】
小船的实际运动是水平向左的运动,它的速度vx可以产生两个效果:一是使绳子OP段缩短;二是使OP段绳与竖直方向的夹角减小.所以小船的速度vx应有沿OP绳指向O的分速度v0和垂直OP的分速度v1,由运动的分解可求得
α角逐渐变大,可得vx是逐渐变大的,所以小船做的是变速运动。
故选A。
10.C
【详解】
A. 因为静水中速度的大小小于水流速度的大小,则合速度的方向不可能垂直河岸,所以小船不可能到达正对岸.故A错误,B错误;
C. 当小船在静水速与河岸垂直时,渡河的时间最短,则最短时间t=d/v静=150/3s=50s.故C正确;
D. 将小船的速度沿河岸和垂直河岸分解,只要小船有垂直河岸方向的分量,就能到达河对岸,故D错误;
故选C
11.B
【详解】
要使小船避开危险区沿直线到达对岸,则有合运动的最大位移为100m.因此已知小船能安全到达河岸的合速度,设此速度与水流速度的夹角为θ,即有:sinθ=,所以θ=30°;又已知流水速度,则可得小船在静水中最小速度为:v船=v水sinθ=×2m/s=1m/s故选B.
12.D
【详解】
对于A,它的速度如图中标出的vA,这个速度看成是A的合速度,其分速度分别是va,vb,
其中va就是B的速度vB(同一根绳子,大小相同),刚开始时B的速度为vB=vAcosα;当A环上升至与定滑轮的连线处于水平位置时,va=0,所以B的速度vB=0,故AB错误;因A匀速上升时,由公式vB=vAcosα,当A上升时,夹角α增大,因此B做向下减速运动,则处于超重状态,由牛顿第二定律,可知绳对B的拉力大于B的重力,故C错误、D正确;
13.B
【详解】
A.飞机起飞后的合速度与合加速度方向一致,所以飞机运动轨迹为直线,A错误;
B.10s内水平方向位移
竖直方向位移
B正确;
C.飞机飞行方向与水平方向夹角的正切,C错误;
D.飞机在20s内水平方向的位移
则平均速度为
D错误。
故选B。
14.B
【详解】
轮与轴同轴转动,角速度相同,所以根据公式可得,船的速度速度可分解为轴上细绳的速度和垂直绳子斜向下的速度,根据几何知识可得,故B正确;
15.D
【解析】
消防员参与了沿梯子方向的匀加速直线运动和水平方向上的匀速直线运动,通过合速度与合加速度是否在同一条直线上判断消防员做直线运动还是曲线运动.若消防车匀速前进,根据运动的合成,知合速度的方向与加速度的方向不在同一条直线,其加速度的方向大小不变,所以消防员做匀变速曲线运动,故A错误
将消防员的运动分解为水平方向和竖直方向,知水平方向上的最终的速度为匀速后退的速度和沿梯子方向速度在水平方向上的分速度的合速度,因为沿梯子方向的速度在水平方向上的分速度在变,所以消防队员水平方向的速度在变.故B错误
若消防车匀加速前进,根据运动的合成,知合速度的方向与合加速度的方向有可能在同一条直线,其加速度的方向大小不变,所以消防员有可能做匀变速直线运动,故C错误
若消防车匀减速前进,根据运动的合成,知合速度的方向与合加速度的方向不在同一条直线,其加速度的方向大小不变,所以消防员做匀变速曲线运动,故D正确
16.84s 140s
【详解】
[1]当船头垂直河岸渡河时,渡河时间最短
[2] 小船以最短距离过河时,则静水中的速度斜着向上游,合速度垂直河岸,则由矢量合成的平行四边形法则,那么船垂直河岸行驶的速度为
渡河最小位移是420m,所以渡河时间为
17.200m 50s
【详解】
[1][2]因为船速大于水速,故合速度可以垂直河岸,则最短航程为河宽200m。根据几何关系可知此时船的合速度
则最短航程渡河时间
18.1
【详解】
[1][2]如图所示,当小船在静水中的速度与其在河流中的速度垂直时,小船在静水中的速度最小,且最小值
此时小船航行的实际速度大小
19.(1) 匀变速曲线运动;(2),方向与x轴成53°;(3)108.2m,方向与x轴成;180m,方向沿x轴。
【详解】
(1) 由图可看出,物体沿x方向的分运动为匀速直线运动,沿y方向的分运动为匀变速直线运动,故合运动为匀变速曲线运动。
(2) 物体的初速度
方向与x轴成53°
(3) 在前3s内
,
故
方向与x轴成。
在前6s内
sx′=vxt′=30×6m=180m,sy′=0
故
s′=sx′=180m
方向沿x轴。
20.(1)船头指向对岸,40s,233 m;(2)航行速度v2与岸成53°,50s
【详解】
(1)当船头指向对岸时,渡河时间最短,如图甲所示
最短渡河时间
船经过的位移大小
(2)欲使船航行距离最短,需使船的实际位移(合位移)与河岸垂直,设此时船的航行速度v2与岸成角,如图乙所示。则
故航行速度v2与岸成53°;船航行的实际速度为
渡河时间
21.3m/s,方向斜向上游河岸,且与河岸成53°角,12.5s
【详解】
小船到达危险水域前,恰好到达对岸,如图所示
设合位移s的方向与河岸成θ角,则
故
小船的合速度方向与合位移方向相同,由平行四边形定则可知,只有当小船相对于静水的速度与合速度方向垂直时,小船相对于静水的速度最小。由图知,此最小速度为
其方向斜向上游河岸,且与河岸成53°角。
合速度为
合位移为
渡河所用时间为
