2021-2022学年人教版A版(2019)高中数学必修一5.5 三角恒等变换 测试卷word版含答案
文档属性
| 名称 | 2021-2022学年人教版A版(2019)高中数学必修一5.5 三角恒等变换 测试卷word版含答案 | 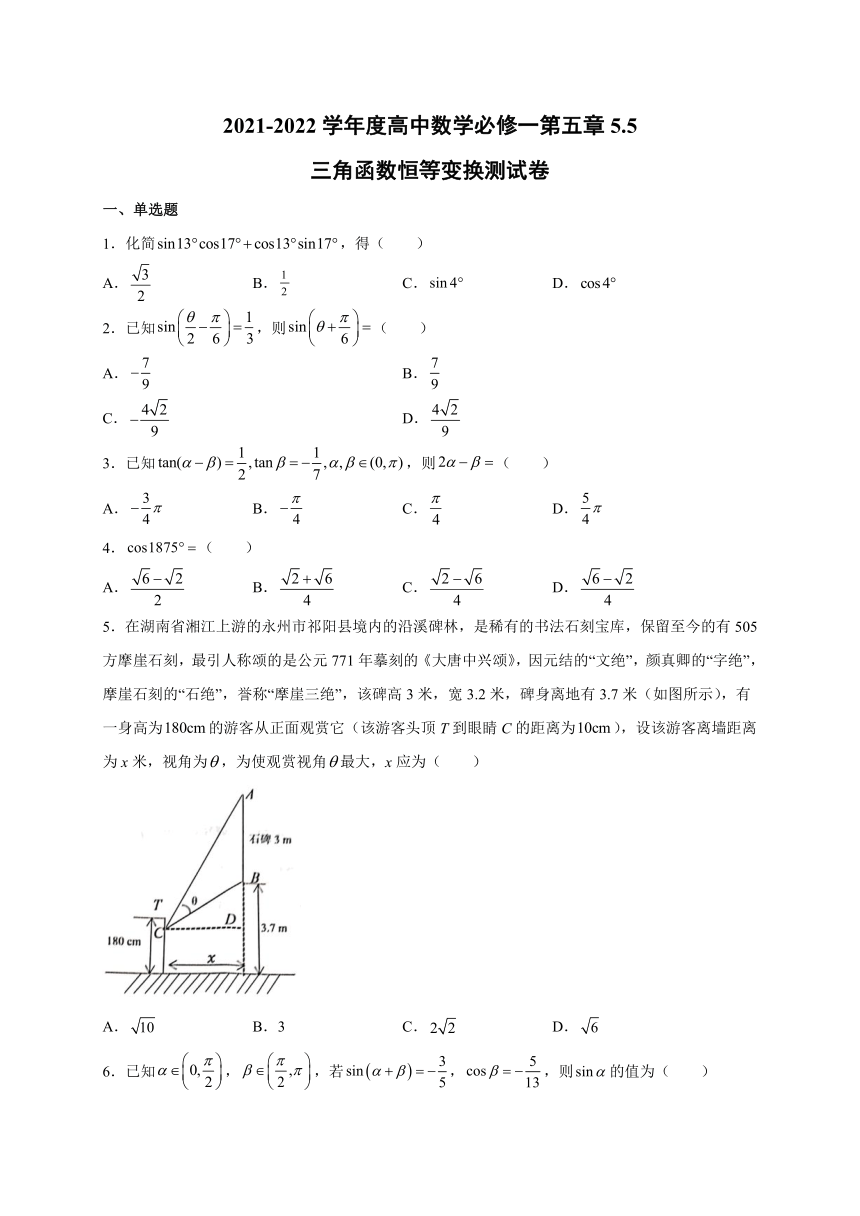 | |
| 格式 | docx | ||
| 文件大小 | 559.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-06 15:44:37 | ||
图片预览





文档简介
2021-2022学年度高中数学必修一第五章5.5
三角函数恒等变换测试卷
一、单选题
1.化简,得( )
A. B. C. D.
2.已知,则( )
A. B.
C. D.
3.已知,则( )
A. B. C. D.
4.( )
A. B. C. D.
5.在湖南省湘江上游的永州市祁阳县境内的沿溪碑林,是稀有的书法石刻宝库,保留至今的有505方摩崖石刻,最引人称颂的是公元771年摹刻的《大唐中兴颂》,因元结的“文绝”,颜真卿的“字绝”,摩崖石刻的“石绝”,誉称“摩崖三绝”,该碑高3米,宽3.2米,碑身离地有3.7米(如图所示),有一身高为的游客从正面观赏它(该游客头顶T到眼睛C的距离为),设该游客离墙距离为x米,视角为,为使观赏视角最大,x应为( )
A. B.3 C. D.
6.已知,,若,,则的值为( )
A. B. C. D.
7.已知,,则的值为( ).
A. B. C.3 D.
8.已知,,则( )
A. B. C. D.
9.将函数的图象向右平移个单位长度,得到函数的图象关于对称,则的最小值为( )
A. B. C. D.
10.已知点在圆:上,从出发,沿圆周逆时针方向运动了弧长()到达点,且,又点在角终边上,则( )
A. B. C. D.
二、填空题
11.已知为锐角,且,则_____________.
12.已知,则_______.
13.求值: _____.
14.若点关于轴对称点为,则的一个取值为_____.
15.已知函数,则
①在上的最小值是1;
②的最小正周期是;
③直线是图象的对称轴;
④直线与的图象恰有2个公共点.
其中说法正确的是________________.
16.若函数的最小正周期为,则函数在上的值域为_______.
三、解答题
17.已知函数
(1)求的最小正周期及其图象对称轴的方程
(2)求在区间上的最大值和最小值.
18.已知,,求的值.
19.求下列各函数的周期和值域:
(1);
(2).
20.已知函数.
(1)若,求的值;
(2)求的值域.
21.利用和(差)角公式,求下列各式的值:
(1);
(2);
(3);
(4).
试卷第1页,共3页
参考答案
1.B
.
故选:B
2.B
解:
故选:B
3.A
因为,
所以,
则,
因为,
则,
所以,
,
所以,
故选:A
4.D
.
故选:D
5.A
设,由图可知,
,
由基本不等式知,当,即时,最大,从而角最大.
故选:A
6.D
因为,,
所以,
又,
则,,
又,
所以,
所以,
,
故选:D
7.A
.
故选:A.
8.B
因为,所以,
因为,所以,
所以,
整理可得:,
所以,
故选:B.
9.A
,
所以,
因为函数的图象关于对称,所以,
所以,因为,所以时,最小,
故选:A.
10.D
因为,
,
,
,
.
故选:D
11.
设,可得,则,可得,
由三角函数的基本关系式,可得,
则.
故答案为:.
12.
,,
即,.
故答案为:.
13.
由,
可得,
又由,
所以.
故答案为:
14.(答案不唯一)
点关于轴对称的点坐标为,则由题可知,,即,,,所以,;同理,即,所以,则,则的一个取值可以为.
故答案为:(答案不唯一)
15.①③④
解:对于①,当时,
且,则当时,函数取最小值,即,故①正确;
对于②,∵,,,则:
故函数的最小正周期不是,②错误;
对于③,若k为奇数,则;
若k为偶数,则.
由上可知,当吋,,
所以,直线是图象的对称轴,③正确;
対于④,因为∵,
所以为函数的周期.
当时,;
当时,.
综上可知,.
当时,,,即函数与在上的图象无交点:
当时,,,所以,函数与在上的图象也无交点.作出函数与函数在上的图象如下图所示:
由图像可知,直线与的图象恰有2个公共点,故④正确.
故答案为:①③④.
16.
由题可知:,
所以
由,所以
所以,所以
所以函数的值域为
故答案为:
17.
(1)最小正周期为,对称轴方程为,.
(2)最小值为,最大值为;
(1)
解:因为
所以,
函数的最小正周期;
令,,解得,,可得它的对称轴方程为,.
(2)
解:因为,所以,所以,所以,故当,即时,函数取得最小值为;当,即时,函数取得最大值为2.
18.
因为,,
所以,
所以,
.
19.
(1)周期为,值域为
(2)周期为,值域为
(1)
∵,
∴函数的周期为,
∵,
∴,即的值域为.
(2)
∵,
∴函数的周期为,
∵,
∴,即的值域为.
20.
(1)
(2)
(1)
,
因为,平方得,
所以.
.
(2)
令,
,则,
,
当时取得最小值;当时取得最大值.
所以的值域为.
21.
(1)
(2)
(3)
(4)
(1)
.
(2)
.
(3)
.
(4)
.答案第1页,共2页
答案第1页,共2页
三角函数恒等变换测试卷
一、单选题
1.化简,得( )
A. B. C. D.
2.已知,则( )
A. B.
C. D.
3.已知,则( )
A. B. C. D.
4.( )
A. B. C. D.
5.在湖南省湘江上游的永州市祁阳县境内的沿溪碑林,是稀有的书法石刻宝库,保留至今的有505方摩崖石刻,最引人称颂的是公元771年摹刻的《大唐中兴颂》,因元结的“文绝”,颜真卿的“字绝”,摩崖石刻的“石绝”,誉称“摩崖三绝”,该碑高3米,宽3.2米,碑身离地有3.7米(如图所示),有一身高为的游客从正面观赏它(该游客头顶T到眼睛C的距离为),设该游客离墙距离为x米,视角为,为使观赏视角最大,x应为( )
A. B.3 C. D.
6.已知,,若,,则的值为( )
A. B. C. D.
7.已知,,则的值为( ).
A. B. C.3 D.
8.已知,,则( )
A. B. C. D.
9.将函数的图象向右平移个单位长度,得到函数的图象关于对称,则的最小值为( )
A. B. C. D.
10.已知点在圆:上,从出发,沿圆周逆时针方向运动了弧长()到达点,且,又点在角终边上,则( )
A. B. C. D.
二、填空题
11.已知为锐角,且,则_____________.
12.已知,则_______.
13.求值: _____.
14.若点关于轴对称点为,则的一个取值为_____.
15.已知函数,则
①在上的最小值是1;
②的最小正周期是;
③直线是图象的对称轴;
④直线与的图象恰有2个公共点.
其中说法正确的是________________.
16.若函数的最小正周期为,则函数在上的值域为_______.
三、解答题
17.已知函数
(1)求的最小正周期及其图象对称轴的方程
(2)求在区间上的最大值和最小值.
18.已知,,求的值.
19.求下列各函数的周期和值域:
(1);
(2).
20.已知函数.
(1)若,求的值;
(2)求的值域.
21.利用和(差)角公式,求下列各式的值:
(1);
(2);
(3);
(4).
试卷第1页,共3页
参考答案
1.B
.
故选:B
2.B
解:
故选:B
3.A
因为,
所以,
则,
因为,
则,
所以,
,
所以,
故选:A
4.D
.
故选:D
5.A
设,由图可知,
,
由基本不等式知,当,即时,最大,从而角最大.
故选:A
6.D
因为,,
所以,
又,
则,,
又,
所以,
所以,
,
故选:D
7.A
.
故选:A.
8.B
因为,所以,
因为,所以,
所以,
整理可得:,
所以,
故选:B.
9.A
,
所以,
因为函数的图象关于对称,所以,
所以,因为,所以时,最小,
故选:A.
10.D
因为,
,
,
,
.
故选:D
11.
设,可得,则,可得,
由三角函数的基本关系式,可得,
则.
故答案为:.
12.
,,
即,.
故答案为:.
13.
由,
可得,
又由,
所以.
故答案为:
14.(答案不唯一)
点关于轴对称的点坐标为,则由题可知,,即,,,所以,;同理,即,所以,则,则的一个取值可以为.
故答案为:(答案不唯一)
15.①③④
解:对于①,当时,
且,则当时,函数取最小值,即,故①正确;
对于②,∵,,,则:
故函数的最小正周期不是,②错误;
对于③,若k为奇数,则;
若k为偶数,则.
由上可知,当吋,,
所以,直线是图象的对称轴,③正确;
対于④,因为∵,
所以为函数的周期.
当时,;
当时,.
综上可知,.
当时,,,即函数与在上的图象无交点:
当时,,,所以,函数与在上的图象也无交点.作出函数与函数在上的图象如下图所示:
由图像可知,直线与的图象恰有2个公共点,故④正确.
故答案为:①③④.
16.
由题可知:,
所以
由,所以
所以,所以
所以函数的值域为
故答案为:
17.
(1)最小正周期为,对称轴方程为,.
(2)最小值为,最大值为;
(1)
解:因为
所以,
函数的最小正周期;
令,,解得,,可得它的对称轴方程为,.
(2)
解:因为,所以,所以,所以,故当,即时,函数取得最小值为;当,即时,函数取得最大值为2.
18.
因为,,
所以,
所以,
.
19.
(1)周期为,值域为
(2)周期为,值域为
(1)
∵,
∴函数的周期为,
∵,
∴,即的值域为.
(2)
∵,
∴函数的周期为,
∵,
∴,即的值域为.
20.
(1)
(2)
(1)
,
因为,平方得,
所以.
.
(2)
令,
,则,
,
当时取得最小值;当时取得最大值.
所以的值域为.
21.
(1)
(2)
(3)
(4)
(1)
.
(2)
.
(3)
.
(4)
.答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
