人教版高中数学课件:对数函数的图像和性质
文档属性
| 名称 | 人教版高中数学课件:对数函数的图像和性质 |  | |
| 格式 | zip | ||
| 文件大小 | 716.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-10-14 08:01:19 | ||
图片预览








文档简介
(共34张PPT)
对数函数的概念与图象
新课讲解:
(一).对数函数的定义:
函数
叫做对数函数;
其中x是自变量,函数的定义域是(0,+∞).
注意:1 对数函数的定义与指数函数类似,都是形式定义,
2 对数函数对底数的限制:
且
判断是不是对数函数
(1)
(2)
(×)
(×)
(×)
(×)
(×)
(×)
(×)
哈哈 ,我们都不是对数函数
你答对了吗???
我们是对数型函数
请认清我们哈
例1 已知函数f(x)为对数函数,且图象过点(4, 2),求f(1),f(8)
讲解范例
解: ①要使函数有意义,则
∴函数的定义域是{x|x≠0}
例2:求下列函数的定义域:
①y=logax2 ②y=loga(4-x)
② 要使函数有意义,则
∴函数的定义域是{x |x<4 }
学习函数的一般模式(方法):
解析式(定义)
图像
性质
应用
数形结合
①定义域
②值域
③单调性
⑤奇偶性
④最值
在同一坐标系中用描点法画出对数函数
的图象。
作图步骤: ①列表,
②描点,
③用平滑曲线连接。
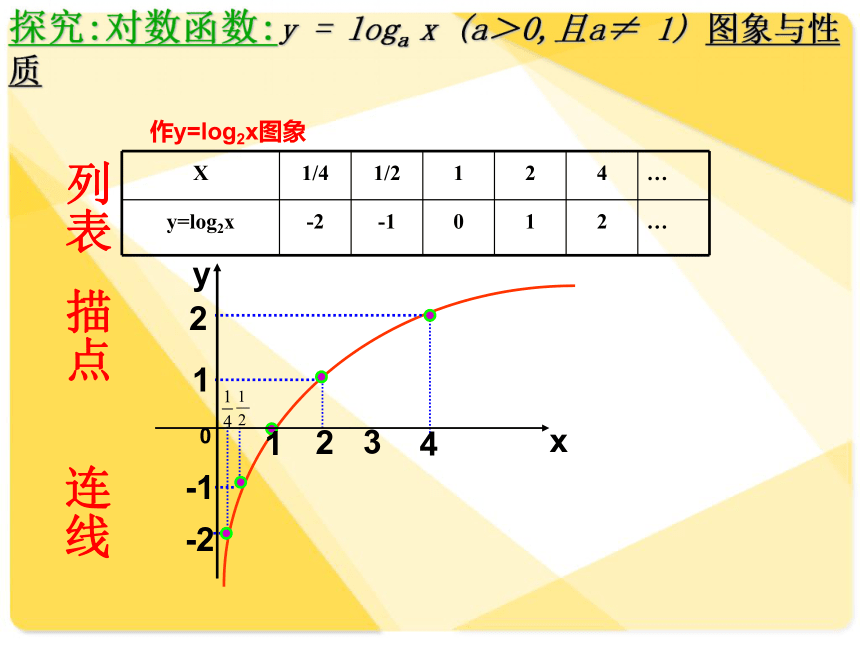
探究:对数函数:y = loga x (a>0,且a≠ 1) 图象与性质
X 1/4 1/2 1 2 4 …
y=log2x -2 -1 0 1 2 …
列表
描点
作y=log2x图象
连线
2
1
-1
-2
1
2
4
0
y
x
3
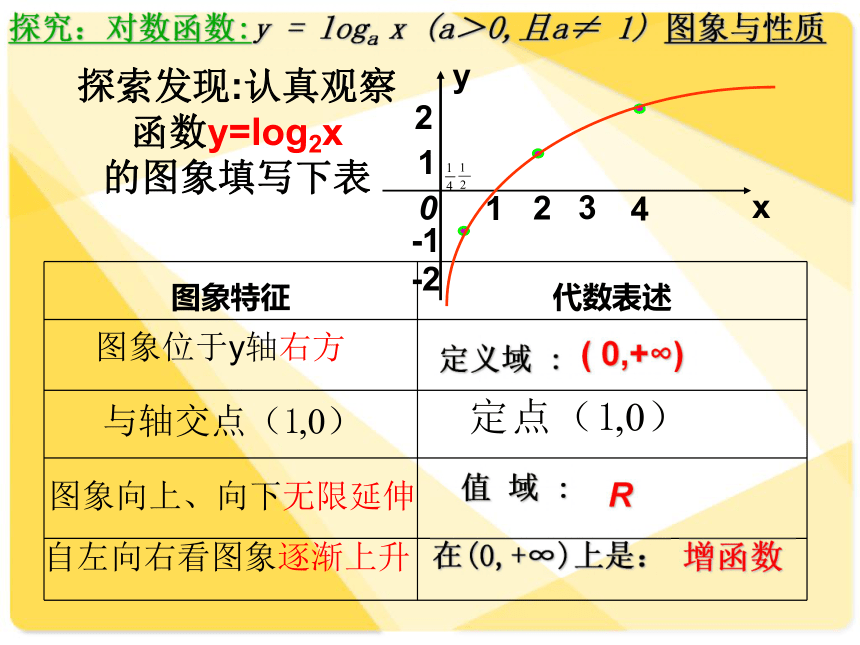
探究:对数函数:y = loga x (a>0,且a≠ 1) 图象与性质
图象特征 代数表述
定义域 :
( 0,+∞)
值 域 :
R
增函数
在(0,+∞)上是:
探索发现:认真观察函数y=log2x
的图象填写下表
图象位于y轴右方
图象向上、向下无限延伸
自左向右看图象逐渐上升
探究:对数函数:y = loga x (a>0,且a≠ 1) 图象与性质
2
1
-1
-2
1
2
4
0
y
x
3
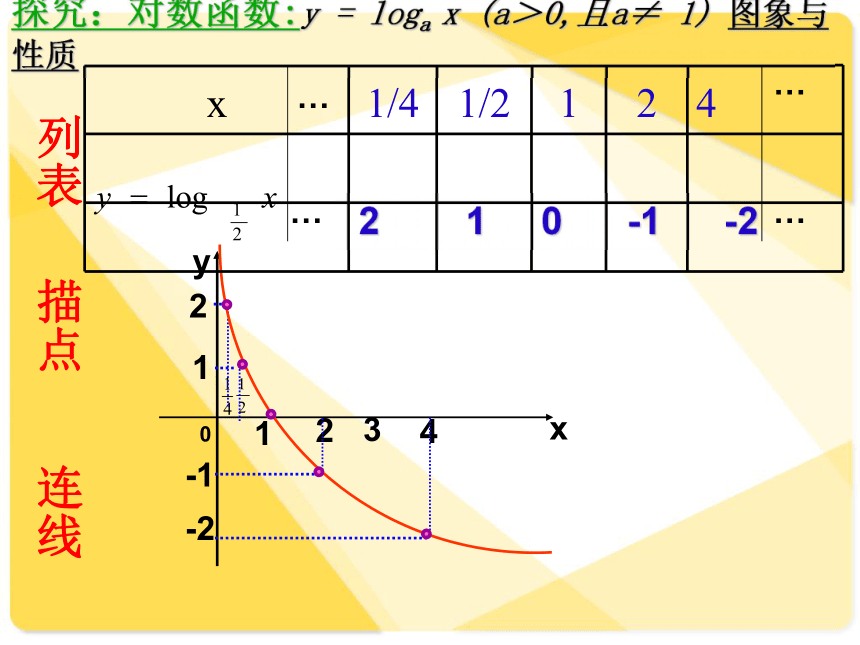
列表
描点
连线
2
1
-1
-2
1
2
4
0
y
x
3
x 1/4 1/2 1 2 4
2 1 0 -1 -2
探究:对数函数:y = loga x (a>0,且a≠ 1) 图象与性质
…
…
…
…
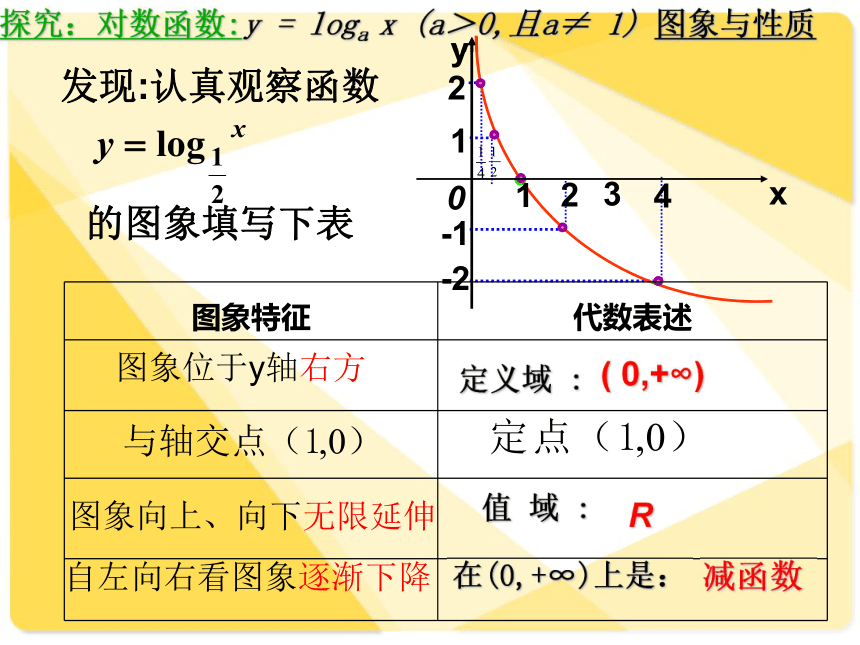
探究:对数函数:y = loga x (a>0,且a≠ 1) 图象与性质
发现:认真观察函数
的图象填写下表
2
1
-1
-2
1
2
4
0
y
x
3
图象特征 代数表述
定义域 :
( 0,+∞)
值 域 :
R
减函数
在(0,+∞)上是:
图象位于y轴右方
图象向上、向下无限延伸
自左向右看图象逐渐下降
2.对数函数的图象和性质
a>1
图
象
性
质 定义域
值域
特殊点
单调性
奇偶性
最值
过点(1,0)
在(0,+ )上是增函数
在(0,+ )上是减函数
当x>1时,y>0;
当0(0,+ )
R
非奇非偶函数
非奇非偶函数
0过点(1,0)
无最值
无最值
y
X
O
x =1
(1,0)
y
X
O
x =1
(1,0)
(0,+ )
R
当x>1时,y<0;
当00.
我很重要
例2 比较下列各组数中两个值的大小:
⑴ log 23.4 , log 28.5
⑵ log 0.31.8 , log 0.32.7
⑶ log a5.1 , log a5.9 ( a>0 , a≠1 )
解:⑴∵对数函数y = log 2x
在(0,+∞)上是增函数
∴ log 23.4<log 28.5
⑵∵对数函数 y = log 0.3 x,
在(0,+∞)上是减函数,
∴log 0.31.8>log 0.32.7
且 3.4<8.5
且1.8<2.7
(3)当a>1时,函数y=log ax在(0,+∞)上是增函数,于是
log a5.1<log a5.9
log a5.1>log a5.9
当0<a<1时,函数y=log ax在(0,+∞)上是减函数,于是
两个同底对数比较大小,构造一个对数函数,然后用单调性比较
你能口答吗?
变一变还能口答吗?
<
,则m___n;
则m___n.
>
<
>
练习1:比较大小
① log76 1 ② log0.53 1
③ log67 1 ④ log0.60.1 1
⑤ log35.1 0 ⑥ log0.12 0
⑦ log20.8 0 ⑧ log0.20.6 0
<
<
<
>
>
>
<
>
① 因为log35 > log33 =1
log53 < log55 =1
得:log 35 > log 53
例.比较大小
(1) log35 log53
② 因为log 32 > 0
log 20.8 < 0
得:log 32 > log 20.8
当底数不相同,真数也不相同时,
方法
10
>
>
常需引入中间值0或1(各种变形式).
解:
(2) log32 log20.8
例 比较大小:
1) log64 log74
解:
方法
当底数不相同,真数相同时,写成倒数形式比较大小
11
<
小结: 1.正确理解对数函数的定义; 2.掌握对数函数的图象和性质; 3.能利用对数函数的性质解决有关问题.
作业:P73 2
3.(2),(3)
X 1/4 1/2 1 2 4 …
y=log2x -2 -1 0 1 2 …
列表
描点
作y=log2x图象
连线
2
1
-1
-2
1
2
4
0
y
x
3
探究:对数函数:y = loga x (a>0,且a≠ 1) 图象与性质
列表
描点
连线
2
1
-1
-2
1
2
4
0
y
x
3
x 1/4 1/2 1 2 4
2 1 0 -1 -2
-2 -1 0 1 2
这两个函数的图象有什么关系呢?
关于x轴对称
探究:对数函数:y = loga x (a>0,且a≠ 1) 图象与性质
…
…
…
…
…
…
对数函数 的图象。
猜猜:
2
1
-1
-2
1
2
4
0
y
x
3
2
1
-1
-2
1
2
4
0
y
x
3
对数函数在第一象限越靠近y轴底数越大
1
y
x
o
0< c< d < 1< a < b
C d 1 a b
由下面对数函数的图像判断底数a,b,c,d的大小
例 比较大小:
1) log53 log43
解:
利用对数函数图象
得到 log53 < log43
方法
当底数不相同,真数相同时,利用图象判断大小.
11
<
y1=log4x
y2=log5x
x
o
y
1
3
例1、求下列函数所过的定点坐标。
知识应用 ----定点问题
总结:求对数函数的定点坐标方法是__?
令真数为1,求出X值即为定点的横坐标,
求出Y值即为定点的纵坐标.
联想:求指数函数的定点坐标方法是__?
例4.
练习2. 不等式log2(4x+8)>log22x 的解集为 ( )
解:由对数函数的性质及定义域要求,得
∴ x>0
4x+8>0
2x>0
4x+8>2x
x > -2
X>0
x> -4
解对数不等式时 , 注意真数大于零.
A. x>0 B. x> -4 C. x > -2 D. x> 4
A
图 象 性 质
a > 1 0 < a < 1
定义域 :
值 域 :
定 点:
在(0,+∞)上是:
在(0,+∞)上是
对数函数y=logax (a>0且a≠1)的图象与性质
( 0,+∞)
R
(1 ,0),
即当x =1时,y=0
增函数
减函数
y
X
O
x =1
(1,0)
y
X
O
x =1
(1,0)
图 象
性 质
a>1
0y
x
0
y=1
(0,1)
y=ax
(a>1)
y
x
(0,1)
y=1
0
y=ax
(0定 义 域 :
值 域 :
定 点:
在 R 上是
在 R 上是
R
(0 , + ∞)
( 0 , 1 ) ,即 x = 0 时, y = 1 .
增函数
减函数
x>0,y>1;
x<0,y>1;
x<0, 0x>0,0回顾指数函数的图像及其性质
类比可得对数函数的图象及性质
y=log x
2
深入探究:函数 与 的图象关系
y=2
X
x … 1/4 1/2 1 2 4 16 …
y=log2x … 1 …
x … -2 -1 0 1 2 4 …
y=2x … …
观察(1):
从下表中你能发现两个函数变量间的什么关系
关系:二者的变量x,y的值互换,即:---
1/4
1/2
1
2
4
16
-2
-1
0
1
2
4
深入探究:函数 与 的图象关系
y=2
X
y=log x
2
观察(2):
从图象中你能发现两个函数的图象间有什么关系
2
1
-1
-2
1
2
4
0
y
x
3
y=log x
2
y=2
X
y=x
A●
●A*
B ●
●
B*
结论(1):图象关于直线y=x对称。
深入探究:
观察(2):
从图象中你能发现两个函数的图象间有什么关系
2
1
-1
-2
1
2
4
0
y
x
3
y=x
B ●
●
B*
结论:图象关于直线y=x对称。
结论(2):函数 与 互为反函数。
阅读教材P73—反函数
y=a
X
y=log x
a
深入探究:函数 与 的图象关系
y=2
X
y=log x
2
观察(2):
从图象中你能发现两个函数的图象间有什么关系
2
1
-1
-2
1
2
4
0
y
x
3
y=log x
2
y=2
X
y=x
A●
●A*
B ●
●
B*
结论(1):图象关于直线y=x对称。
结论(2):函数 与 互为反函数。
阅读教材P73—反函数
y=a
X
y=log x
a
作业: P74.习题2.2 A组
7,8
B组 2题
对数函数的概念与图象
新课讲解:
(一).对数函数的定义:
函数
叫做对数函数;
其中x是自变量,函数的定义域是(0,+∞).
注意:1 对数函数的定义与指数函数类似,都是形式定义,
2 对数函数对底数的限制:
且
判断是不是对数函数
(1)
(2)
(×)
(×)
(×)
(×)
(×)
(×)
(×)
哈哈 ,我们都不是对数函数
你答对了吗???
我们是对数型函数
请认清我们哈
例1 已知函数f(x)为对数函数,且图象过点(4, 2),求f(1),f(8)
讲解范例
解: ①要使函数有意义,则
∴函数的定义域是{x|x≠0}
例2:求下列函数的定义域:
①y=logax2 ②y=loga(4-x)
② 要使函数有意义,则
∴函数的定义域是{x |x<4 }
学习函数的一般模式(方法):
解析式(定义)
图像
性质
应用
数形结合
①定义域
②值域
③单调性
⑤奇偶性
④最值
在同一坐标系中用描点法画出对数函数
的图象。
作图步骤: ①列表,
②描点,
③用平滑曲线连接。
探究:对数函数:y = loga x (a>0,且a≠ 1) 图象与性质
X 1/4 1/2 1 2 4 …
y=log2x -2 -1 0 1 2 …
列表
描点
作y=log2x图象
连线
2
1
-1
-2
1
2
4
0
y
x
3
探究:对数函数:y = loga x (a>0,且a≠ 1) 图象与性质
图象特征 代数表述
定义域 :
( 0,+∞)
值 域 :
R
增函数
在(0,+∞)上是:
探索发现:认真观察函数y=log2x
的图象填写下表
图象位于y轴右方
图象向上、向下无限延伸
自左向右看图象逐渐上升
探究:对数函数:y = loga x (a>0,且a≠ 1) 图象与性质
2
1
-1
-2
1
2
4
0
y
x
3
列表
描点
连线
2
1
-1
-2
1
2
4
0
y
x
3
x 1/4 1/2 1 2 4
2 1 0 -1 -2
探究:对数函数:y = loga x (a>0,且a≠ 1) 图象与性质
…
…
…
…
探究:对数函数:y = loga x (a>0,且a≠ 1) 图象与性质
发现:认真观察函数
的图象填写下表
2
1
-1
-2
1
2
4
0
y
x
3
图象特征 代数表述
定义域 :
( 0,+∞)
值 域 :
R
减函数
在(0,+∞)上是:
图象位于y轴右方
图象向上、向下无限延伸
自左向右看图象逐渐下降
2.对数函数的图象和性质
a>1
图
象
性
质 定义域
值域
特殊点
单调性
奇偶性
最值
过点(1,0)
在(0,+ )上是增函数
在(0,+ )上是减函数
当x>1时,y>0;
当0
R
非奇非偶函数
非奇非偶函数
0
无最值
无最值
y
X
O
x =1
(1,0)
y
X
O
x =1
(1,0)
(0,+ )
R
当x>1时,y<0;
当0
我很重要
例2 比较下列各组数中两个值的大小:
⑴ log 23.4 , log 28.5
⑵ log 0.31.8 , log 0.32.7
⑶ log a5.1 , log a5.9 ( a>0 , a≠1 )
解:⑴∵对数函数y = log 2x
在(0,+∞)上是增函数
∴ log 23.4<log 28.5
⑵∵对数函数 y = log 0.3 x,
在(0,+∞)上是减函数,
∴log 0.31.8>log 0.32.7
且 3.4<8.5
且1.8<2.7
(3)当a>1时,函数y=log ax在(0,+∞)上是增函数,于是
log a5.1<log a5.9
log a5.1>log a5.9
当0<a<1时,函数y=log ax在(0,+∞)上是减函数,于是
两个同底对数比较大小,构造一个对数函数,然后用单调性比较
你能口答吗?
变一变还能口答吗?
<
,则m___n;
则m___n.
>
<
>
练习1:比较大小
① log76 1 ② log0.53 1
③ log67 1 ④ log0.60.1 1
⑤ log35.1 0 ⑥ log0.12 0
⑦ log20.8 0 ⑧ log0.20.6 0
<
<
<
>
>
>
<
>
① 因为log35 > log33 =1
log53 < log55 =1
得:log 35 > log 53
例.比较大小
(1) log35 log53
② 因为log 32 > 0
log 20.8 < 0
得:log 32 > log 20.8
当底数不相同,真数也不相同时,
方法
10
>
>
常需引入中间值0或1(各种变形式).
解:
(2) log32 log20.8
例 比较大小:
1) log64 log74
解:
方法
当底数不相同,真数相同时,写成倒数形式比较大小
11
<
小结: 1.正确理解对数函数的定义; 2.掌握对数函数的图象和性质; 3.能利用对数函数的性质解决有关问题.
作业:P73 2
3.(2),(3)
X 1/4 1/2 1 2 4 …
y=log2x -2 -1 0 1 2 …
列表
描点
作y=log2x图象
连线
2
1
-1
-2
1
2
4
0
y
x
3
探究:对数函数:y = loga x (a>0,且a≠ 1) 图象与性质
列表
描点
连线
2
1
-1
-2
1
2
4
0
y
x
3
x 1/4 1/2 1 2 4
2 1 0 -1 -2
-2 -1 0 1 2
这两个函数的图象有什么关系呢?
关于x轴对称
探究:对数函数:y = loga x (a>0,且a≠ 1) 图象与性质
…
…
…
…
…
…
对数函数 的图象。
猜猜:
2
1
-1
-2
1
2
4
0
y
x
3
2
1
-1
-2
1
2
4
0
y
x
3
对数函数在第一象限越靠近y轴底数越大
1
y
x
o
0< c< d < 1< a < b
C d 1 a b
由下面对数函数的图像判断底数a,b,c,d的大小
例 比较大小:
1) log53 log43
解:
利用对数函数图象
得到 log53 < log43
方法
当底数不相同,真数相同时,利用图象判断大小.
11
<
y1=log4x
y2=log5x
x
o
y
1
3
例1、求下列函数所过的定点坐标。
知识应用 ----定点问题
总结:求对数函数的定点坐标方法是__?
令真数为1,求出X值即为定点的横坐标,
求出Y值即为定点的纵坐标.
联想:求指数函数的定点坐标方法是__?
例4.
练习2. 不等式log2(4x+8)>log22x 的解集为 ( )
解:由对数函数的性质及定义域要求,得
∴ x>0
4x+8>0
2x>0
4x+8>2x
x > -2
X>0
x> -4
解对数不等式时 , 注意真数大于零.
A. x>0 B. x> -4 C. x > -2 D. x> 4
A
图 象 性 质
a > 1 0 < a < 1
定义域 :
值 域 :
定 点:
在(0,+∞)上是:
在(0,+∞)上是
对数函数y=logax (a>0且a≠1)的图象与性质
( 0,+∞)
R
(1 ,0),
即当x =1时,y=0
增函数
减函数
y
X
O
x =1
(1,0)
y
X
O
x =1
(1,0)
图 象
性 质
a>1
0
x
0
y=1
(0,1)
y=ax
(a>1)
y
x
(0,1)
y=1
0
y=ax
(0
值 域 :
定 点:
在 R 上是
在 R 上是
R
(0 , + ∞)
( 0 , 1 ) ,即 x = 0 时, y = 1 .
增函数
减函数
x>0,y>1;
x<0,y>1;
x<0, 0
类比可得对数函数的图象及性质
y=log x
2
深入探究:函数 与 的图象关系
y=2
X
x … 1/4 1/2 1 2 4 16 …
y=log2x … 1 …
x … -2 -1 0 1 2 4 …
y=2x … …
观察(1):
从下表中你能发现两个函数变量间的什么关系
关系:二者的变量x,y的值互换,即:---
1/4
1/2
1
2
4
16
-2
-1
0
1
2
4
深入探究:函数 与 的图象关系
y=2
X
y=log x
2
观察(2):
从图象中你能发现两个函数的图象间有什么关系
2
1
-1
-2
1
2
4
0
y
x
3
y=log x
2
y=2
X
y=x
A●
●A*
B ●
●
B*
结论(1):图象关于直线y=x对称。
深入探究:
观察(2):
从图象中你能发现两个函数的图象间有什么关系
2
1
-1
-2
1
2
4
0
y
x
3
y=x
B ●
●
B*
结论:图象关于直线y=x对称。
结论(2):函数 与 互为反函数。
阅读教材P73—反函数
y=a
X
y=log x
a
深入探究:函数 与 的图象关系
y=2
X
y=log x
2
观察(2):
从图象中你能发现两个函数的图象间有什么关系
2
1
-1
-2
1
2
4
0
y
x
3
y=log x
2
y=2
X
y=x
A●
●A*
B ●
●
B*
结论(1):图象关于直线y=x对称。
结论(2):函数 与 互为反函数。
阅读教材P73—反函数
y=a
X
y=log x
a
作业: P74.习题2.2 A组
7,8
B组 2题
