2021-2022学年苏科版八年级数学上册6.4用一次函数解决问题 同步达标测评(Word版含答案)
文档属性
| 名称 | 2021-2022学年苏科版八年级数学上册6.4用一次函数解决问题 同步达标测评(Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 315.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-03 14:34:39 | ||
图片预览




文档简介
2021-2022学年苏科版八年级数学上册《6.4用一次函数解决问题》同步达标测评(附答案)
一.选择题(共6小题,满分30分)
1.甲、乙两位同学周末相约骑自行车去游玩,沿同一路线从A地出发前往B地,甲、乙分别以不同的速度匀速骑行,甲比乙早出发5分钟.甲骑行20分钟后,乙以原速的1.5倍继续骑行,经过一段时间,乙先到达B地,甲一直保持原速前往B地.在此过程中,甲、乙两人相距的路程y(单位:m)与甲骑行的时间x(单位:min)之间的关系如图所示,则下列说法中错误的是( )
A.甲的骑行速度是250m/min
B.A,B两地的总路程为22.5km
C.乙出发60min后追上甲
D.甲比乙晚5min到达B地
2.一条公路旁依次有A,B,C三个村庄,甲、乙两人骑自行车分别从A村、B村同时出发前往C村,甲、乙之间的距离s(km)与骑行时间t(h)之间的函数关系如图所示,下列结论:①A,B两村相距10km;②甲出发2h后到达C村;③甲每小时比乙多骑行8km;④相遇后,乙又骑行了30min或55min时两人相距4km.其中正确的是( )
①③④ B.①②③
C.①②④ D.①②③④
3.如图,A.B两地之间的路程为6000米,甲、乙两人骑车都从A地出发,已知甲先出发5分钟后,乙才出发,乙在A、B之间的C地追赶上甲,当乙追赶上甲后,乙立即返回A地,甲继续往B地前行.甲到达B地后停止骑行,乙骑行到达A地时也停止(乙在C地掉头时间忽略不计).在整个骑行过程中,甲和乙都保持各自速度匀速骑行,甲乙两人相距的路程y(米)与甲出发的时间x(分钟)之间的关系如图所示.下列说法正确的是( )
①乙的速度为227.5米/分;②甲的速度为150米/分;③图中M点的坐标为(21,2940);④乙到达A地时,甲与B地相距3060米.
A.①②③ B.②③④ C.①③④ D.①②④
4.甲、乙两名运动员同时从A地出发前往B地,在笔直的公路上进行骑自行车训练.如图所示,反映了甲、乙两名运动员在公路上进行训练时的行驶路程S(千米)与行驶时间t(小时)之间的关系,下列四种说法:①甲的速度为40千米/小时;②乙的速度始终为50千米/小时;③行驶1小时时,乙在甲前10千米处;④甲、乙两名运动员相距5千米时,t=0.5或t=2.其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
5.容积为1500升的蓄水池装有一个进水管和一个出水管,单位时间内进、出水量都一定,单开进水管30分钟可把空池注满,单开出水管20分钟可把满池的水放尽.现水池内有水250升,先打开进水管10分钟后,再两管同时开放,直至把池中的水放完.这一过程中蓄水池中的蓄水量y(升)随时间x(分)变化的图象是( )
A.B.C.D.
6.一辆货车和一辆小轿车同时从甲地出发,货车匀速行驶至乙地,小轿车中途停车休整后提速行驶至乙地,货车的路程y1(km),小轿车的路程y2(km)与时间x(h)的对应关系如图所示,下列结论错误的是( )
A.甲、乙两地的距离为420km
B.y1=60x,y2=
C.货车出发4.5h与小轿车首次相遇
D.两车首次相遇时距乙地150km
二.填空题(共6小题,满分30分)
7.小明租用共享单车从家出发,匀速骑行到相距2400米的图书馆还书.小明出发的同时,他的爸爸以每分钟96米的速度从图书馆沿同一条道路步行回家,小明在图书馆停留了2分钟后沿原路按原速返回.设他们出发后经过t(分)时,小明与家之间的距离为s1(米),小明爸爸与家之间的距离为s2(米),图中折线OABD、线段EF分别表示s1、s2与t之间的函数关系的图象小明从家出发,经过 分钟在返回途中追上爸爸.
8.实验室里有一个水平放置的长方体容器,从内部量得它的高是15cm,底面的长是30cm,宽是20cm,容器内的水深为xcm.现往容器内放入如图的长方体实心铁块(铁块一面平放在容器底面),过顶点A的三条棱的长分别10cm,10cm,ycm(y≤15),当铁块的顶部高出水面2cm时,x,y满足的关系式是 .
9.在青山区“海绵城市”工程中,某工程队接受一段道路施工的任务,计划从2016年10月初至2017年9月底(12个月)完成.施工3个月后,实行倒计时,提高工作效率,剩余工程量与施工时间的关系如图所示,那么按提高工作效率后的速度做完全部工程,则工期可缩短 个月.
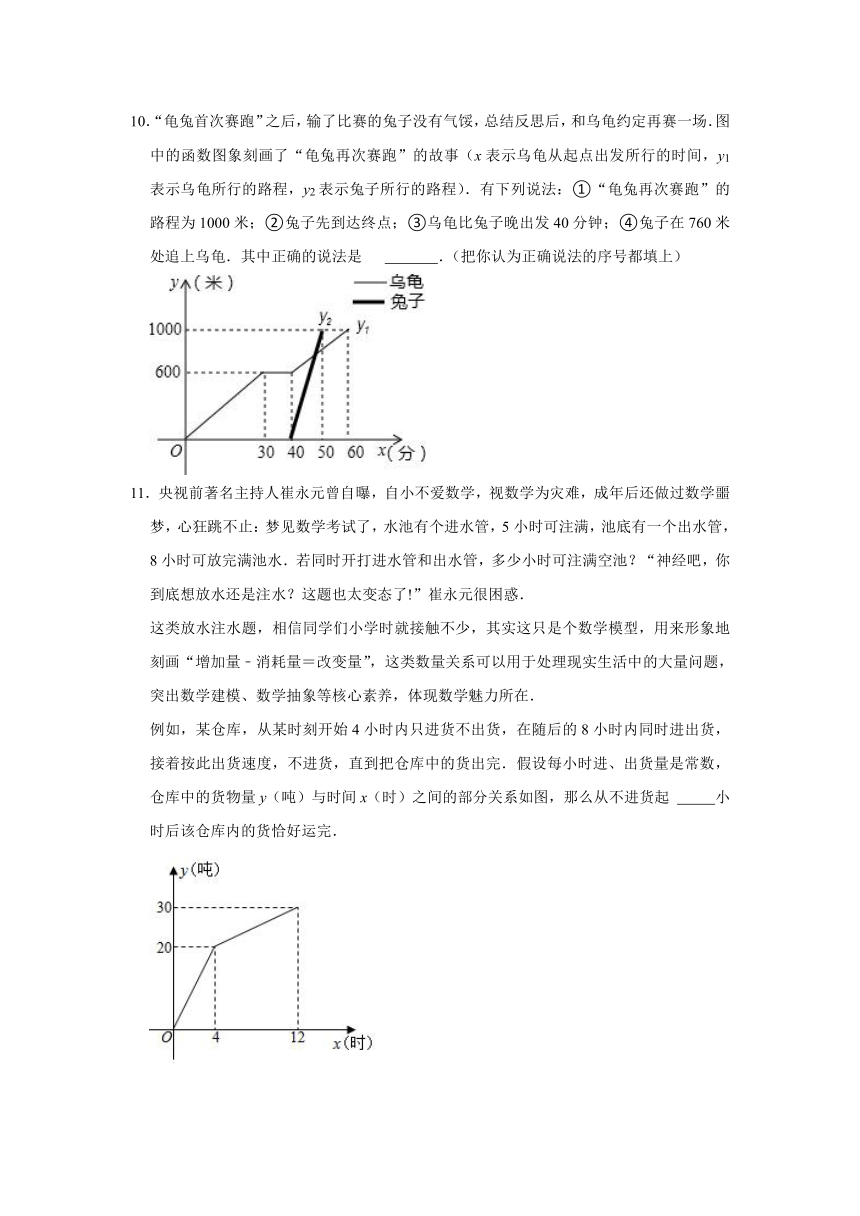
10.“龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结反思后,和乌龟约定再赛一场.图中的函数图象刻画了“龟兔再次赛跑”的故事(x表示乌龟从起点出发所行的时间,y1表示乌龟所行的路程,y2表示兔子所行的路程).有下列说法:①“龟兔再次赛跑”的路程为1000米;②兔子先到达终点;③乌龟比兔子晚出发40分钟;④兔子在760米处追上乌龟.其中正确的说法是 .(把你认为正确说法的序号都填上)
11.央视前著名主持人崔永元曾自曝,自小不爱数学,视数学为灾难,成年后还做过数学噩梦,心狂跳不止:梦见数学考试了,水池有个进水管,5小时可注满,池底有一个出水管,8小时可放完满池水.若同时开打进水管和出水管,多少小时可注满空池?“神经吧,你到底想放水还是注水?这题也太变态了!”崔永元很困惑.
这类放水注水题,相信同学们小学时就接触不少,其实这只是个数学模型,用来形象地刻画“增加量﹣消耗量=改变量”,这类数量关系可以用于处理现实生活中的大量问题,突出数学建模、数学抽象等核心素养,体现数学魅力所在.
例如,某仓库,从某时刻开始4小时内只进货不出货,在随后的8小时内同时进出货,接着按此出货速度,不进货,直到把仓库中的货出完.假设每小时进、出货量是常数,仓库中的货物量y(吨)与时间x(时)之间的部分关系如图,那么从不进货起 小时后该仓库内的货恰好运完.
12.某市规定了每月用水不超过18立方米和超过18立方米两种不同的收费标准,该市用户每月应交水费y(元)是用水x(立方米)的函数,其图象如图所示.已知小丽家3月份交了水费102元,则小丽家这个月用水量为 立方米.
三.解答题(共8小题,满分60分)
13.为了保障羊肉正常供应,某畜牧集团的A,B两个养殖场共出栏肥羊2000只,B养殖场的肥羊数量是A养殖场的2倍少400只.这批肥羊将运往甲地1300只,乙地700只,运费如下表(单位:元/只).
养殖场目的地 A B
甲 25 18
乙 20 24
(1)求A,B养殖场各出栏多少只肥羊?
(2)设这批肥羊从A养殖场运往甲地x只(100≤x≤700),全部运往甲、乙两地的总费用为y元,求y与x的函数关系式,并设计使总运费最少的调运方案;
(3)当每只肥羊的运费下降a元(0<a≤18且a为整数)时,按(2)中设计的调运方案,总运费不超过30000元,求a的最小值.
14.某市长虹电器专卖店经销A型号彩电,今年四月份每台彩电售价为2000元,与去年同期相比,结果卖出彩电的数量相同,但去年销售额为5万元,今年销售额只有4万元.
(1)问去年四月份每台A型号彩电售价是多少元?
(2)为了改善经营,长虹电器专卖店决定再经销B型号彩电.已知A型号彩电每台进货价为1800元,B型号彩电每台进货价为1500元,电器城预计用不多于3.3万元且不少于3.2万元的资金购进这两种彩电共20台,问有哪几种进货方案?
(3)在(2)条件下,今年因原材料涨价,A型彩电每台实际进货价涨价a元(50≤a≤120),如果售价按2200元/台的价格出售,B型号彩电进货价不变,以每台1800元的价格出售,在这批彩电全部卖出的前提下,根据a的情况如何进货才能使专卖店获得最大利润?最大利润是多少(用含a的式子表示)?
15.小明从A地匀速前往B地,同时小亮从B地匀速前往A地,如图表示两人距B地的路程y(m)与行驶时间x(min)之间的函数关系.
马小虎审题不清,将“两人距B地的路程y”看成了“两人距A地的路程y”,由此得到小明的速度为100m/min.
(1)A地与B地的距离为 m,a= m,b= min,小明的实际速度为 m/min;
(2)求当0≤x≤60时,两人的距离s(m)与x的函数表达式,并在图2中画出图象;
(3)当两人之间的距离不大于2000m时,直接写出x的取值范围.
16.某市A,B两个蔬菜基地得知四川C,D两个灾民安置点分别急需蔬菜240t和260t的消息后,决定调运蔬菜支援灾区,已知A蔬菜基地有蔬菜200t,B蔬菜基地有蔬菜300t,现将这些蔬菜全部调运C,D两个灾区安置点从A地运往C,D两处的费用分别为每吨20元和25元,从B地运往C,D两处的费用分别为每吨15元和18元.设从B地运往C处的蔬菜为x吨.
(1)请填写下表,并求两个蔬菜基地调运蔬菜的运费相等时x的值:
C D 总计/t
A 200
B x 300
总计/t 240 260 500
(2)设A,B两个蔬菜基地的总运费为w元,求出w与x之间的函数关系式,并求总运费最小的调运方案;
(3)经过抢修,从B地到C处的路况得到进一步改善,缩短了运输时间,运费每吨减少m元(m>0),其余线路的运费不变,试讨论总运费最小的调动方案.
17.小军和爸爸同时从家骑自行车去图书馆,爸爸先以150米/分的速度骑行一段时间,休息了5分钟,再以m米/分的速度到达图书馆,小军始终以同一速度骑行,两人行驶的路程y(米)与时间x(分)的关系如图所示,请结合图象,解答下列问题:
(1)a= b= ,m= ;
(2)若小军的速度是120米/分,求小军在途中与爸爸第二次相遇时,距图书馆的距离;
(3)在(2)的条件下,爸爸自第二次出发至到达图书馆前,何时与小军相距100米?
18.双十一期间,当当网上某书店销售图书《帕丁顿系列一》,每套售价80元,共销售了3000套;利润y(百元)关于套数x(百套)之间的函数如图所示,当销售超过1000套时,该店需向当当网额外支付5000元的平台使用费(不列入书的成本费用).
当销售套数不超过1000套时,利润=书籍收入﹣成本费用;当销售套数超过1000套时,利润=书籍收入﹣成本费用﹣平台使用费.
(1)当销售不超过1000套时,求利润y(百元)关于销售套数x(百套)的函数解析式和成本费用w(百元)关于销售套数x(百套)的函数解析式;
(2)若利润为28000元,售出了多少套数,需支付的成本费用是多少元?
19.甲车从A地出发匀速驶向B地,到达B地后,立即按原路原速返回A地;乙车从B地出发沿相同路线匀速驶向A地,出发t(t>0)小时后,乙车因故在途中停车1小时,然后继续按原速驶向A地,乙车在行驶过程中的速度是80千米/时,甲车比乙车早1小时到达A地,两车距各自出发地的路程y千米与甲车行驶时间x小时之间的函数关系如图所示,请结合图象信息,解答下列问题:
(1)写出甲车行驶的速度,并直接在图中的( )内填上正确的数;
(2)求甲车从B地返回A地的过程中,y与x的函数解析式(不需要写出自变量x的取值范围);
(3)若从乙车出发至甲车到达A地,两车恰好有两次相距80千米,直接写出t的取值范围.
20.某公司组织30辆汽车装运A、B、C三种产品共125吨到外地销售,规定每辆汽车只装运一种产品,且必须装满;装运每种产品的汽车不少于4辆;同时装运的B种产品的重量不超过装运的A、C两种产品重量和.
(1)设用x辆汽车装运A种产品,用y辆汽车装运B种产品,根据下表提供的信息,求y与x之间的函数关系式并写出自变量的x取值范围.
产品品种 A B C
每辆汽车装运量(吨) 5 4 3
每吨产品获利(万元) 0.6 0.7 0.8
(2)设此次外销活动的利润为Q(万元),求Q与x之间的函数关系式,并求出怎样装运才能获得最大利润.
(3)由于市场行情的变化,将A、C两种产品每吨售价提高a万元(0.01≤a≤0.03),其他条件不变,求销售这批产品获得最大利润的方案.
参考答案
一.选择题(共6小题,满分30分)
1.解:甲5min骑行1250m,故速度为1250÷5=250m/min,
故A正确;
设乙的速度为xm/min,则有20×250﹣15x=2000,
解得:x=200,
∴乙的速度为200m/min,
甲骑行20分钟后,乙以原速的1.5倍,即1.5×200=300m/min继续骑行,
∵乙先到达B地,
∴由题意可得AB两地的总路程为15×200+(85﹣20)×300=22500m=22.5km,
故B正确;
乙出发tmin后追上甲,
则(t+5)×250=15×200+(t﹣15)×300,
解得t=55,即乙出发55min后追上甲,
故C错误.
85min甲的路程为85×250=21250(m),
∴甲比乙晚=5 min到达B地,
故D正确.
故选:C.
2.解:由图象可知A村、B村相离10km,
故①正确,
当1.25h时,甲、乙相距为0km,故在此时相遇,说明甲的速度大于乙的速度,
当2h时,甲到达C村,
故②正确;
v甲×1.25﹣v乙×1.25=10,
解得:v甲﹣v乙=8,
故甲的速度比乙的速度快8km/h,
故③正确;
当1.25≤t≤2时,函数图象经过点(1.25,0)(2,6),
设一次函数的解析式为s=kt+b,
代入得:,
解得:,
∴s=8t﹣10
当s=4时,得4=8t﹣10,
解得t=1.75h
由1.75﹣1.25=0.5h=30(min),
同理当2≤t≤2.5时,设函数解析式为s=kt+b
将点(2,6)(2.5,0)代入得:
,
解得:,
∴s=﹣12t+30
当s=4时,得4=﹣12t+30,
解得t=,
由﹣1.25=h=55min
故相遇后,乙又骑行了30min或55min时两人相距4km,
故④正确.
故选:D.
3.解:由图象可得,
甲的速度为:700÷5=140(米/分);
乙的速度为:140×13÷(13﹣5)=227.5(米/分),
乙骑行到A地时,甲骑车用的时间为:13+(13﹣5)=21(分),
乙骑行到达A地时,甲乙两人相距的路程140×21=2940(米),
故M点的坐标为(21,2940);
故乙到达A地时,甲与B地相距的路程是:6000﹣140×21=3060(米),
综上所述,①③④说法正确.
故选:C.
4.解:①甲的速度为=40,故正确;
②t≤1时,已的速度为=50,t>1后,乙的速度为=35,故错误;
③行驶1小时时,甲走了40千米,乙走了50千米,乙在甲前10千米处,故正确;
④由①②③得:甲的函数表达式为:y=40x,
已的函数表达为:0≤t≤1时,y=50x,t>1时,y=35x+15,
t=0.5时,甲、乙两名运动员相距=50×﹣40×=5,
t=2时,甲、乙两名运动员相距=(35×2+15)﹣2×40=5,
同理t=4时,甲、乙两名运动员相距为5,故错误.
故选:B.
5.解:因为进水速度是1500÷30=50升/分,单开出水管20分钟可把满池的水放尽,则出水速度是1500÷20=75升/分,
所以先打开进水管10分钟,水池中有250+50×10=750升的水,两管同时开放,直至把水池中的水放完共用了750÷(75﹣50)=30分钟,
故10+30=40(分钟)
故选:A.
6.解:A、由图象可得,甲乙两地的距离是420km,
∴选项A正确;
B、设货车的路程y1与x的函数关系式为y1=kx,小轿车的路程y2与x的函数关系式为y2=mx+n,
将(7,420)代入y1=kx中,
420=7k,解得:k=60,
∴货车的路程y1与x的函数关系式为y1=60x;
当x=5.75时,y1=60x=60×5.75=345,
将(5.75,345)、(6.5,420)代入y2=mx+n中,
,解得:,
∴y2=100x﹣230(5≤x≤6.5).
当x=5时,y2=100x﹣230=100×5﹣230=270,
将(0,0)、(3,270)代入y2=mx+n中,
,解得:,
∴y2=90x(0≤x≤3).
∴y2=,
∴选项B错误;
C、令y1=60x=270,解得:x=4.5,
∴货车出发4.5h与小轿车首次相遇,选项C正确;
D、∵货车出发4.5h与小轿车首次相遇,
∴y1=60x=60×4.5=270,
∴420﹣270=150(km),
∴两车首次相遇时距乙地150km,选项D正确.
故选:B.
二.填空题(共6小题,满分30分)
7.解:由题意得:B(12,2400),D(22,0),F(25,0),E(0,2400)
设直线BD、EF的关系式分别为s1=k1t+b1,s2=k2t+b2,
把B(12,2400),D(22,0),F(25,0),E(0,2400)代入相应的关系式得:
,,
解得:,,
直线BD、EF的关系式分别为s1=﹣240t+5280,s2=﹣96t+2400,
当s1=s2时,即:﹣240t+5280=﹣96t+2400,
解得:t=20,
故答案为:20.
8.解:①当长方体实心铁块的棱长为10cm和ycm的那一面平放在长方体的容器底面时,
则铁块浸在水中的高度为8cm,
此时,水位上升了(8﹣x)cm(x<10﹣2=8),铁块浸在水中的体积为10×8×y=80ycm3,
∴80y=30×20×(8﹣x),
∴y=,
∵y≤15,
∴x≥6,
即:y=(6≤x<8),
②当长方体实心铁块的棱长为10cm和10cm的那一面平放在长方体的容器底面时,
同①的方法得,y=,
∵y≤15,
∴≤15,
∴x≤,
∴0<x≤,
故答案为:y=(0<x≤)或y=(6≤x<8)
9.解:观察图象可知:开始3个月的工作效率:,还需要9个月完成任务.
接下来3个月的工作效率:[(1﹣)﹣]÷3=,还需要÷=个月完成任务.
∴按提高工作效率后的速度做完全部工程,则工期可缩短9﹣=1.5个月,
故答案为1.5
10.解:由函数图象可得,
“龟兔再次赛跑”的路程为1000米,故①说法正确;
兔子先到达终点,故②说法正确;
兔子比乌龟晚出发40分钟,故③说法错误;
当40≤x≤60时,设y1与x的函数关系式为y1=kx+b,
∵点(40,600),(60,1000)在该函数图象上,
∴,
解得,
∴当40≤x≤60时,y1与x的函数关系式为y1=20x﹣200;
当40≤x≤50时,设y2与x的函数关系式为y2=mx+n,
∵点(40,0),(50,1000)在该函数图象上,
∴,
解得,
即当40≤x≤50时,y2与x的函数关系式为y2=100x﹣4000;
令20x﹣200=100x﹣4000,
解得x=47.5,
∴当x=47.5时,此时y1=y2=750,
即兔子在750米处追上乌龟,故④错误;
故答案为:①②.
11.解:由图像可知:从0至4小时,进货20吨,
故进货速度为每小时5吨.
∵从4小时到12小时仓库货物增加了(30﹣20)吨,
∴经过8小时仓库货物增加了10吨.
∴出货的速度为:(5×8﹣10)÷8=(吨).
∴从不进货起,需要30÷=8小时后该仓库内的货恰好运完.
故答案为:8.
12.解:设当x>18时的函数解析式为y=kx+b,
,得,
即当x>18时的函数解析式为y=4x﹣18,
∵102>54,
∴当y=102时,102=4x﹣18,得x=30,
故答案为:30.
三.解答题(共8小题,满分60分)
13.解:(1)设A养殖场出栏m只肥羊,B养殖场出栏 (2m﹣400)只肥羊,根据题意得:
m+2m﹣400=2000,
解得:m=800.
答:A养殖场出栏800只肥羊,B养殖场出栏1200只肥羊;
(2)设这批肥羊从A养殖场运往甲地x只,则从A养殖场运往乙地(800﹣x)只,
从B养殖场运往甲地(1300﹣x)只,从B养殖场运往乙地 (x﹣100)只,
根据题意得:y=25x+20(800﹣x)+18(1300﹣x)+24(×﹣100)=11x+37000,
∵11>0,
∴y随x的增大而增大,
∵100≤x≤700,
∴x=100时,y最小,
答:这批肥羊从A养殖场运往甲地100只,则从A养殖场运往乙地700只,从B养殖场运往甲地1200只,此时费用最少;
(3)总运费z=100(25﹣x)+700(20﹣a)+1200(18﹣a)=﹣2000a+38100,
由题意得:,
解得:4.05≤a≤18,且a为整数,
∴a的最小值为5.
14.解:(1)设去年四月份每台A型号彩电售价x元,依题意得:
=,
解得:x=2500,
经检验,x=2500是原方程的解,
答:去年四月份每台A型号彩电售价是2500元;
(2)设专卖店在此次进货中,购进A型号彩电m台,则B型号彩电(20﹣m)台,依题意得:
,
解得:≤m≤10,
由于m只取非负整数,所以m=7,8,9,10,
所以电器城在此次进货中,共有4种进货方案,分别是:
方案一:购进A型号彩电7台、B型号彩电13台;
方案二:购进A型号彩电8台、B型号彩电12台;
方案三:购进A型号彩电9台、B型号彩电11台;
方案四:购进A型号彩电10台、B型号彩电10台;
(3)设A型号彩电购进y台,专卖店获得的利润为w元,则B型号彩电购进(20﹣y)台,
由题意得:w=(2200﹣1800﹣a)y+(1800﹣1500)(20﹣y),
整理得:w=(100﹣a)y+6000,
分以下三种情况:
①当50≤a<100时,100﹣a>0,
由一次函数的性质可知,w随少的增大而增大,
则当y=10时,w取最大值,最大值为10(100﹣a)+6000=7000﹣10a,
即此时A型号彩电购进10台,B型号彩电购进10台才能使专卖店获得最大利润,最大利润是(7000﹣10a)元;
②当a=100时,w=6000,
则此时按(2)的四种进货方案均可使专卖店获得最大利润,最大利润是6000元;
③当100<a≤120时,100﹣a<0,
由一次函数的性质可知,w随y的增大而减小,
则当y=7时,w取最大值,最大值为7(100﹣a)+6000=6700﹣7a,
即此时A型号彩电购进7台,B型号彩电购进13台才能使专卖店获得最大利润,最大利润是(6700﹣7a)元;
综上,当50≤a<100时,A型号彩电购进10台,B型号彩电购进10台才能使专卖店获得最大利润,最大利润是(7000﹣10a)元;当a=100时,按(2)的四种进货方案均可使专卖店获得最大利润,最大利润是6000元;当100<a≤120时,A型号彩电购进7台,B型号彩电购进13台才能使专卖店获得最大利润,最大利润是(6700﹣7a)元.
15.解:(1)由图象可得,
A地与B地的距离为4500m,
a=100×15=1500,
b=4500÷[(4500﹣1500)÷20]=30,
小明的实际速度为:4500÷30=150(m/min),
故答案为:4500,1500,30,150;
(2)由题意可得,
小亮的实际速度为:1500÷15=100(m/min),
当0≤x≤15时,s=4500﹣(150+100)x=﹣250x+4500;
当15<x≤20时,s=4500﹣(150+100)×15﹣150(x﹣15)=﹣150x+3000;
当20<x≤30时,s=150(x﹣20)=150x﹣3000;
当30<x≤60时,s=1500+100(x﹣30)=100x﹣1500;
综上,s与x的关系式为:s=;
图象如图1:
(3)如图2所示,
当y=2000时,﹣250x+4500=2000,
∴x=10,
100x﹣1500=2000,
∴x=35,
∴当两人之间的距离不大于2000m时,x的取值范围是10≤x≤35.
16.解:(1)填表如下:
C D 总计/t
A (240﹣x) (x﹣40) 200
B x (300﹣x) 300
总计/t 240 260 500
依题意得:20(240﹣x)+25(x﹣40)=15x+18(300﹣x)
解得:x=200
两个蔬菜基地调运蔬菜的运费相等时x的值为200.
(2)w与x之间的函数关系为:w=20(240﹣x)+25(x﹣40)+15x+18(300﹣x)=2x+9200
由题意得:
∴40≤x≤240
∵在w=2x+9200中,2>0
∴w随x的增大而增大
∴当x=40时,总运费最小
此时调运方案为:
(3)由题意得w=(2﹣m)x+9200
∴0<m<2,(2)中调运方案总费用最小;
m=2时,在40≤x≤240的前提下调运方案的总费用不变;
2<m<15时,x=240总费用最小,其调运方案如下:
17.解:(1)1500÷150=10(分钟),
10+5=15(分钟),
(3000﹣1500)÷(22.5﹣15)=200(米/分).
故答案为:10;15;200.
(2)BC段关系式为:y1=200x﹣1500,
OD段关系式为:y2=120x,
相遇时,即y1=y2,即120x=200x﹣1500
解得:x=18.75
此时:y1=y2=2250
距离图书馆:3000﹣2250=750(米)
答:小军在途中与爸爸第二次相遇时,距图书馆的距离是750米.
(3)当y1﹣y2=100时,解得x=20
当y2﹣y1=100时,解得x=17.5
答:爸爸自第二次出发至到达图书馆前,17.5分钟时和20分钟时与小军相距100米.
(2)旅客最多可免费携带30千克的行李.
18.解:(1)当0≤x≤10时,设y=kx﹣200,把(10,300)代入,得300=10x﹣200,
解得k=50,
∴y=50x﹣200;
w=80x﹣y=80x﹣(50x﹣200)=30x+200;
(2)当10≤x≤30时,设y=ax+b,把(30,1250),(10,250)代入,得
,
解得,
∴y=50x﹣250;
①当50x﹣200=280时,解得x=9.6,即960套,
w=30×9.6+200=488(百元)=48800(元);
②当50x﹣250=280时,解得x=10.6,即1060套,
w=30×10.6+200=568(百元)=56800(元).
答:若利润为28000元,售出了960套,需支付的成本费用是48800元;或售出了1060套,需支付的成本费用是56800元.
19.解:(1)400÷80+1+3=9,甲的速度=千米/小时
(2)由题意可得:E点坐标为(8,0),D(4,400)
设DE解析式y=kx+b
∴
解得:k=﹣100,b=800
∴解析式y=﹣100x+800
(3)根据题意可得:甲车到达B地前,两车恰好有一次相距80千米,
甲车在返回过程中,甲车超过乙车后到达A地的过程中,必有一次两车恰好有两次相距80千米,
即甲车在返回过程中,甲车追上乙车之前的过程中,两车相距不超过80千米,
∴80t<80
∴t<1
∴0<t<1
20.解:(1)由题意得,化简得,
即y与x之间的函数关系式为y=35﹣2x(15≥x≥10);
(2)由题意得:Q=5×0.6x+4 0.7y+3×0.8(30﹣x﹣y)=86﹣0.2x,
当x=10(台)时,Q最大,此时Q的最大值为84(万元);
即装运A、B、C货物的车辆分别为10台、15台、5台时,可以获得最大利润84万元;
(3)设此时外销活动的利润为Q′(万元),
由题意得:
Q′=5x(0.6+a)+4×0.7y+3×(30﹣x﹣y)(0.8+a)=86﹣0.2x+8ax﹣15a=(﹣0.2+8a)x+86﹣15a(15≥x≥10),
①当﹣0.2+8a=0时,有最大利润=86﹣15×=85.625(万元).
②当﹣0.2+8a>0时,即a>0.025,
故当a=0.03时,有最大利润=(﹣0.2+8a)15+86﹣15a=(83+105a)=83+105×0.03=86.15(万元)
③当﹣0.2+8a<0时,即a<﹣0.025,与0.01≤a≤0.03矛盾,故不成立,
故当a=0.03时,有最大利润=(﹣0.2+8a)15+86﹣15a=(83+105a)=83+105×0.03=86.15(万元),
即每吨售价提高0.03万元时,获得的最大利润为86.15万元.
一.选择题(共6小题,满分30分)
1.甲、乙两位同学周末相约骑自行车去游玩,沿同一路线从A地出发前往B地,甲、乙分别以不同的速度匀速骑行,甲比乙早出发5分钟.甲骑行20分钟后,乙以原速的1.5倍继续骑行,经过一段时间,乙先到达B地,甲一直保持原速前往B地.在此过程中,甲、乙两人相距的路程y(单位:m)与甲骑行的时间x(单位:min)之间的关系如图所示,则下列说法中错误的是( )
A.甲的骑行速度是250m/min
B.A,B两地的总路程为22.5km
C.乙出发60min后追上甲
D.甲比乙晚5min到达B地
2.一条公路旁依次有A,B,C三个村庄,甲、乙两人骑自行车分别从A村、B村同时出发前往C村,甲、乙之间的距离s(km)与骑行时间t(h)之间的函数关系如图所示,下列结论:①A,B两村相距10km;②甲出发2h后到达C村;③甲每小时比乙多骑行8km;④相遇后,乙又骑行了30min或55min时两人相距4km.其中正确的是( )
①③④ B.①②③
C.①②④ D.①②③④
3.如图,A.B两地之间的路程为6000米,甲、乙两人骑车都从A地出发,已知甲先出发5分钟后,乙才出发,乙在A、B之间的C地追赶上甲,当乙追赶上甲后,乙立即返回A地,甲继续往B地前行.甲到达B地后停止骑行,乙骑行到达A地时也停止(乙在C地掉头时间忽略不计).在整个骑行过程中,甲和乙都保持各自速度匀速骑行,甲乙两人相距的路程y(米)与甲出发的时间x(分钟)之间的关系如图所示.下列说法正确的是( )
①乙的速度为227.5米/分;②甲的速度为150米/分;③图中M点的坐标为(21,2940);④乙到达A地时,甲与B地相距3060米.
A.①②③ B.②③④ C.①③④ D.①②④
4.甲、乙两名运动员同时从A地出发前往B地,在笔直的公路上进行骑自行车训练.如图所示,反映了甲、乙两名运动员在公路上进行训练时的行驶路程S(千米)与行驶时间t(小时)之间的关系,下列四种说法:①甲的速度为40千米/小时;②乙的速度始终为50千米/小时;③行驶1小时时,乙在甲前10千米处;④甲、乙两名运动员相距5千米时,t=0.5或t=2.其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
5.容积为1500升的蓄水池装有一个进水管和一个出水管,单位时间内进、出水量都一定,单开进水管30分钟可把空池注满,单开出水管20分钟可把满池的水放尽.现水池内有水250升,先打开进水管10分钟后,再两管同时开放,直至把池中的水放完.这一过程中蓄水池中的蓄水量y(升)随时间x(分)变化的图象是( )
A.B.C.D.
6.一辆货车和一辆小轿车同时从甲地出发,货车匀速行驶至乙地,小轿车中途停车休整后提速行驶至乙地,货车的路程y1(km),小轿车的路程y2(km)与时间x(h)的对应关系如图所示,下列结论错误的是( )
A.甲、乙两地的距离为420km
B.y1=60x,y2=
C.货车出发4.5h与小轿车首次相遇
D.两车首次相遇时距乙地150km
二.填空题(共6小题,满分30分)
7.小明租用共享单车从家出发,匀速骑行到相距2400米的图书馆还书.小明出发的同时,他的爸爸以每分钟96米的速度从图书馆沿同一条道路步行回家,小明在图书馆停留了2分钟后沿原路按原速返回.设他们出发后经过t(分)时,小明与家之间的距离为s1(米),小明爸爸与家之间的距离为s2(米),图中折线OABD、线段EF分别表示s1、s2与t之间的函数关系的图象小明从家出发,经过 分钟在返回途中追上爸爸.
8.实验室里有一个水平放置的长方体容器,从内部量得它的高是15cm,底面的长是30cm,宽是20cm,容器内的水深为xcm.现往容器内放入如图的长方体实心铁块(铁块一面平放在容器底面),过顶点A的三条棱的长分别10cm,10cm,ycm(y≤15),当铁块的顶部高出水面2cm时,x,y满足的关系式是 .
9.在青山区“海绵城市”工程中,某工程队接受一段道路施工的任务,计划从2016年10月初至2017年9月底(12个月)完成.施工3个月后,实行倒计时,提高工作效率,剩余工程量与施工时间的关系如图所示,那么按提高工作效率后的速度做完全部工程,则工期可缩短 个月.
10.“龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结反思后,和乌龟约定再赛一场.图中的函数图象刻画了“龟兔再次赛跑”的故事(x表示乌龟从起点出发所行的时间,y1表示乌龟所行的路程,y2表示兔子所行的路程).有下列说法:①“龟兔再次赛跑”的路程为1000米;②兔子先到达终点;③乌龟比兔子晚出发40分钟;④兔子在760米处追上乌龟.其中正确的说法是 .(把你认为正确说法的序号都填上)
11.央视前著名主持人崔永元曾自曝,自小不爱数学,视数学为灾难,成年后还做过数学噩梦,心狂跳不止:梦见数学考试了,水池有个进水管,5小时可注满,池底有一个出水管,8小时可放完满池水.若同时开打进水管和出水管,多少小时可注满空池?“神经吧,你到底想放水还是注水?这题也太变态了!”崔永元很困惑.
这类放水注水题,相信同学们小学时就接触不少,其实这只是个数学模型,用来形象地刻画“增加量﹣消耗量=改变量”,这类数量关系可以用于处理现实生活中的大量问题,突出数学建模、数学抽象等核心素养,体现数学魅力所在.
例如,某仓库,从某时刻开始4小时内只进货不出货,在随后的8小时内同时进出货,接着按此出货速度,不进货,直到把仓库中的货出完.假设每小时进、出货量是常数,仓库中的货物量y(吨)与时间x(时)之间的部分关系如图,那么从不进货起 小时后该仓库内的货恰好运完.
12.某市规定了每月用水不超过18立方米和超过18立方米两种不同的收费标准,该市用户每月应交水费y(元)是用水x(立方米)的函数,其图象如图所示.已知小丽家3月份交了水费102元,则小丽家这个月用水量为 立方米.
三.解答题(共8小题,满分60分)
13.为了保障羊肉正常供应,某畜牧集团的A,B两个养殖场共出栏肥羊2000只,B养殖场的肥羊数量是A养殖场的2倍少400只.这批肥羊将运往甲地1300只,乙地700只,运费如下表(单位:元/只).
养殖场目的地 A B
甲 25 18
乙 20 24
(1)求A,B养殖场各出栏多少只肥羊?
(2)设这批肥羊从A养殖场运往甲地x只(100≤x≤700),全部运往甲、乙两地的总费用为y元,求y与x的函数关系式,并设计使总运费最少的调运方案;
(3)当每只肥羊的运费下降a元(0<a≤18且a为整数)时,按(2)中设计的调运方案,总运费不超过30000元,求a的最小值.
14.某市长虹电器专卖店经销A型号彩电,今年四月份每台彩电售价为2000元,与去年同期相比,结果卖出彩电的数量相同,但去年销售额为5万元,今年销售额只有4万元.
(1)问去年四月份每台A型号彩电售价是多少元?
(2)为了改善经营,长虹电器专卖店决定再经销B型号彩电.已知A型号彩电每台进货价为1800元,B型号彩电每台进货价为1500元,电器城预计用不多于3.3万元且不少于3.2万元的资金购进这两种彩电共20台,问有哪几种进货方案?
(3)在(2)条件下,今年因原材料涨价,A型彩电每台实际进货价涨价a元(50≤a≤120),如果售价按2200元/台的价格出售,B型号彩电进货价不变,以每台1800元的价格出售,在这批彩电全部卖出的前提下,根据a的情况如何进货才能使专卖店获得最大利润?最大利润是多少(用含a的式子表示)?
15.小明从A地匀速前往B地,同时小亮从B地匀速前往A地,如图表示两人距B地的路程y(m)与行驶时间x(min)之间的函数关系.
马小虎审题不清,将“两人距B地的路程y”看成了“两人距A地的路程y”,由此得到小明的速度为100m/min.
(1)A地与B地的距离为 m,a= m,b= min,小明的实际速度为 m/min;
(2)求当0≤x≤60时,两人的距离s(m)与x的函数表达式,并在图2中画出图象;
(3)当两人之间的距离不大于2000m时,直接写出x的取值范围.
16.某市A,B两个蔬菜基地得知四川C,D两个灾民安置点分别急需蔬菜240t和260t的消息后,决定调运蔬菜支援灾区,已知A蔬菜基地有蔬菜200t,B蔬菜基地有蔬菜300t,现将这些蔬菜全部调运C,D两个灾区安置点从A地运往C,D两处的费用分别为每吨20元和25元,从B地运往C,D两处的费用分别为每吨15元和18元.设从B地运往C处的蔬菜为x吨.
(1)请填写下表,并求两个蔬菜基地调运蔬菜的运费相等时x的值:
C D 总计/t
A 200
B x 300
总计/t 240 260 500
(2)设A,B两个蔬菜基地的总运费为w元,求出w与x之间的函数关系式,并求总运费最小的调运方案;
(3)经过抢修,从B地到C处的路况得到进一步改善,缩短了运输时间,运费每吨减少m元(m>0),其余线路的运费不变,试讨论总运费最小的调动方案.
17.小军和爸爸同时从家骑自行车去图书馆,爸爸先以150米/分的速度骑行一段时间,休息了5分钟,再以m米/分的速度到达图书馆,小军始终以同一速度骑行,两人行驶的路程y(米)与时间x(分)的关系如图所示,请结合图象,解答下列问题:
(1)a= b= ,m= ;
(2)若小军的速度是120米/分,求小军在途中与爸爸第二次相遇时,距图书馆的距离;
(3)在(2)的条件下,爸爸自第二次出发至到达图书馆前,何时与小军相距100米?
18.双十一期间,当当网上某书店销售图书《帕丁顿系列一》,每套售价80元,共销售了3000套;利润y(百元)关于套数x(百套)之间的函数如图所示,当销售超过1000套时,该店需向当当网额外支付5000元的平台使用费(不列入书的成本费用).
当销售套数不超过1000套时,利润=书籍收入﹣成本费用;当销售套数超过1000套时,利润=书籍收入﹣成本费用﹣平台使用费.
(1)当销售不超过1000套时,求利润y(百元)关于销售套数x(百套)的函数解析式和成本费用w(百元)关于销售套数x(百套)的函数解析式;
(2)若利润为28000元,售出了多少套数,需支付的成本费用是多少元?
19.甲车从A地出发匀速驶向B地,到达B地后,立即按原路原速返回A地;乙车从B地出发沿相同路线匀速驶向A地,出发t(t>0)小时后,乙车因故在途中停车1小时,然后继续按原速驶向A地,乙车在行驶过程中的速度是80千米/时,甲车比乙车早1小时到达A地,两车距各自出发地的路程y千米与甲车行驶时间x小时之间的函数关系如图所示,请结合图象信息,解答下列问题:
(1)写出甲车行驶的速度,并直接在图中的( )内填上正确的数;
(2)求甲车从B地返回A地的过程中,y与x的函数解析式(不需要写出自变量x的取值范围);
(3)若从乙车出发至甲车到达A地,两车恰好有两次相距80千米,直接写出t的取值范围.
20.某公司组织30辆汽车装运A、B、C三种产品共125吨到外地销售,规定每辆汽车只装运一种产品,且必须装满;装运每种产品的汽车不少于4辆;同时装运的B种产品的重量不超过装运的A、C两种产品重量和.
(1)设用x辆汽车装运A种产品,用y辆汽车装运B种产品,根据下表提供的信息,求y与x之间的函数关系式并写出自变量的x取值范围.
产品品种 A B C
每辆汽车装运量(吨) 5 4 3
每吨产品获利(万元) 0.6 0.7 0.8
(2)设此次外销活动的利润为Q(万元),求Q与x之间的函数关系式,并求出怎样装运才能获得最大利润.
(3)由于市场行情的变化,将A、C两种产品每吨售价提高a万元(0.01≤a≤0.03),其他条件不变,求销售这批产品获得最大利润的方案.
参考答案
一.选择题(共6小题,满分30分)
1.解:甲5min骑行1250m,故速度为1250÷5=250m/min,
故A正确;
设乙的速度为xm/min,则有20×250﹣15x=2000,
解得:x=200,
∴乙的速度为200m/min,
甲骑行20分钟后,乙以原速的1.5倍,即1.5×200=300m/min继续骑行,
∵乙先到达B地,
∴由题意可得AB两地的总路程为15×200+(85﹣20)×300=22500m=22.5km,
故B正确;
乙出发tmin后追上甲,
则(t+5)×250=15×200+(t﹣15)×300,
解得t=55,即乙出发55min后追上甲,
故C错误.
85min甲的路程为85×250=21250(m),
∴甲比乙晚=5 min到达B地,
故D正确.
故选:C.
2.解:由图象可知A村、B村相离10km,
故①正确,
当1.25h时,甲、乙相距为0km,故在此时相遇,说明甲的速度大于乙的速度,
当2h时,甲到达C村,
故②正确;
v甲×1.25﹣v乙×1.25=10,
解得:v甲﹣v乙=8,
故甲的速度比乙的速度快8km/h,
故③正确;
当1.25≤t≤2时,函数图象经过点(1.25,0)(2,6),
设一次函数的解析式为s=kt+b,
代入得:,
解得:,
∴s=8t﹣10
当s=4时,得4=8t﹣10,
解得t=1.75h
由1.75﹣1.25=0.5h=30(min),
同理当2≤t≤2.5时,设函数解析式为s=kt+b
将点(2,6)(2.5,0)代入得:
,
解得:,
∴s=﹣12t+30
当s=4时,得4=﹣12t+30,
解得t=,
由﹣1.25=h=55min
故相遇后,乙又骑行了30min或55min时两人相距4km,
故④正确.
故选:D.
3.解:由图象可得,
甲的速度为:700÷5=140(米/分);
乙的速度为:140×13÷(13﹣5)=227.5(米/分),
乙骑行到A地时,甲骑车用的时间为:13+(13﹣5)=21(分),
乙骑行到达A地时,甲乙两人相距的路程140×21=2940(米),
故M点的坐标为(21,2940);
故乙到达A地时,甲与B地相距的路程是:6000﹣140×21=3060(米),
综上所述,①③④说法正确.
故选:C.
4.解:①甲的速度为=40,故正确;
②t≤1时,已的速度为=50,t>1后,乙的速度为=35,故错误;
③行驶1小时时,甲走了40千米,乙走了50千米,乙在甲前10千米处,故正确;
④由①②③得:甲的函数表达式为:y=40x,
已的函数表达为:0≤t≤1时,y=50x,t>1时,y=35x+15,
t=0.5时,甲、乙两名运动员相距=50×﹣40×=5,
t=2时,甲、乙两名运动员相距=(35×2+15)﹣2×40=5,
同理t=4时,甲、乙两名运动员相距为5,故错误.
故选:B.
5.解:因为进水速度是1500÷30=50升/分,单开出水管20分钟可把满池的水放尽,则出水速度是1500÷20=75升/分,
所以先打开进水管10分钟,水池中有250+50×10=750升的水,两管同时开放,直至把水池中的水放完共用了750÷(75﹣50)=30分钟,
故10+30=40(分钟)
故选:A.
6.解:A、由图象可得,甲乙两地的距离是420km,
∴选项A正确;
B、设货车的路程y1与x的函数关系式为y1=kx,小轿车的路程y2与x的函数关系式为y2=mx+n,
将(7,420)代入y1=kx中,
420=7k,解得:k=60,
∴货车的路程y1与x的函数关系式为y1=60x;
当x=5.75时,y1=60x=60×5.75=345,
将(5.75,345)、(6.5,420)代入y2=mx+n中,
,解得:,
∴y2=100x﹣230(5≤x≤6.5).
当x=5时,y2=100x﹣230=100×5﹣230=270,
将(0,0)、(3,270)代入y2=mx+n中,
,解得:,
∴y2=90x(0≤x≤3).
∴y2=,
∴选项B错误;
C、令y1=60x=270,解得:x=4.5,
∴货车出发4.5h与小轿车首次相遇,选项C正确;
D、∵货车出发4.5h与小轿车首次相遇,
∴y1=60x=60×4.5=270,
∴420﹣270=150(km),
∴两车首次相遇时距乙地150km,选项D正确.
故选:B.
二.填空题(共6小题,满分30分)
7.解:由题意得:B(12,2400),D(22,0),F(25,0),E(0,2400)
设直线BD、EF的关系式分别为s1=k1t+b1,s2=k2t+b2,
把B(12,2400),D(22,0),F(25,0),E(0,2400)代入相应的关系式得:
,,
解得:,,
直线BD、EF的关系式分别为s1=﹣240t+5280,s2=﹣96t+2400,
当s1=s2时,即:﹣240t+5280=﹣96t+2400,
解得:t=20,
故答案为:20.
8.解:①当长方体实心铁块的棱长为10cm和ycm的那一面平放在长方体的容器底面时,
则铁块浸在水中的高度为8cm,
此时,水位上升了(8﹣x)cm(x<10﹣2=8),铁块浸在水中的体积为10×8×y=80ycm3,
∴80y=30×20×(8﹣x),
∴y=,
∵y≤15,
∴x≥6,
即:y=(6≤x<8),
②当长方体实心铁块的棱长为10cm和10cm的那一面平放在长方体的容器底面时,
同①的方法得,y=,
∵y≤15,
∴≤15,
∴x≤,
∴0<x≤,
故答案为:y=(0<x≤)或y=(6≤x<8)
9.解:观察图象可知:开始3个月的工作效率:,还需要9个月完成任务.
接下来3个月的工作效率:[(1﹣)﹣]÷3=,还需要÷=个月完成任务.
∴按提高工作效率后的速度做完全部工程,则工期可缩短9﹣=1.5个月,
故答案为1.5
10.解:由函数图象可得,
“龟兔再次赛跑”的路程为1000米,故①说法正确;
兔子先到达终点,故②说法正确;
兔子比乌龟晚出发40分钟,故③说法错误;
当40≤x≤60时,设y1与x的函数关系式为y1=kx+b,
∵点(40,600),(60,1000)在该函数图象上,
∴,
解得,
∴当40≤x≤60时,y1与x的函数关系式为y1=20x﹣200;
当40≤x≤50时,设y2与x的函数关系式为y2=mx+n,
∵点(40,0),(50,1000)在该函数图象上,
∴,
解得,
即当40≤x≤50时,y2与x的函数关系式为y2=100x﹣4000;
令20x﹣200=100x﹣4000,
解得x=47.5,
∴当x=47.5时,此时y1=y2=750,
即兔子在750米处追上乌龟,故④错误;
故答案为:①②.
11.解:由图像可知:从0至4小时,进货20吨,
故进货速度为每小时5吨.
∵从4小时到12小时仓库货物增加了(30﹣20)吨,
∴经过8小时仓库货物增加了10吨.
∴出货的速度为:(5×8﹣10)÷8=(吨).
∴从不进货起,需要30÷=8小时后该仓库内的货恰好运完.
故答案为:8.
12.解:设当x>18时的函数解析式为y=kx+b,
,得,
即当x>18时的函数解析式为y=4x﹣18,
∵102>54,
∴当y=102时,102=4x﹣18,得x=30,
故答案为:30.
三.解答题(共8小题,满分60分)
13.解:(1)设A养殖场出栏m只肥羊,B养殖场出栏 (2m﹣400)只肥羊,根据题意得:
m+2m﹣400=2000,
解得:m=800.
答:A养殖场出栏800只肥羊,B养殖场出栏1200只肥羊;
(2)设这批肥羊从A养殖场运往甲地x只,则从A养殖场运往乙地(800﹣x)只,
从B养殖场运往甲地(1300﹣x)只,从B养殖场运往乙地 (x﹣100)只,
根据题意得:y=25x+20(800﹣x)+18(1300﹣x)+24(×﹣100)=11x+37000,
∵11>0,
∴y随x的增大而增大,
∵100≤x≤700,
∴x=100时,y最小,
答:这批肥羊从A养殖场运往甲地100只,则从A养殖场运往乙地700只,从B养殖场运往甲地1200只,此时费用最少;
(3)总运费z=100(25﹣x)+700(20﹣a)+1200(18﹣a)=﹣2000a+38100,
由题意得:,
解得:4.05≤a≤18,且a为整数,
∴a的最小值为5.
14.解:(1)设去年四月份每台A型号彩电售价x元,依题意得:
=,
解得:x=2500,
经检验,x=2500是原方程的解,
答:去年四月份每台A型号彩电售价是2500元;
(2)设专卖店在此次进货中,购进A型号彩电m台,则B型号彩电(20﹣m)台,依题意得:
,
解得:≤m≤10,
由于m只取非负整数,所以m=7,8,9,10,
所以电器城在此次进货中,共有4种进货方案,分别是:
方案一:购进A型号彩电7台、B型号彩电13台;
方案二:购进A型号彩电8台、B型号彩电12台;
方案三:购进A型号彩电9台、B型号彩电11台;
方案四:购进A型号彩电10台、B型号彩电10台;
(3)设A型号彩电购进y台,专卖店获得的利润为w元,则B型号彩电购进(20﹣y)台,
由题意得:w=(2200﹣1800﹣a)y+(1800﹣1500)(20﹣y),
整理得:w=(100﹣a)y+6000,
分以下三种情况:
①当50≤a<100时,100﹣a>0,
由一次函数的性质可知,w随少的增大而增大,
则当y=10时,w取最大值,最大值为10(100﹣a)+6000=7000﹣10a,
即此时A型号彩电购进10台,B型号彩电购进10台才能使专卖店获得最大利润,最大利润是(7000﹣10a)元;
②当a=100时,w=6000,
则此时按(2)的四种进货方案均可使专卖店获得最大利润,最大利润是6000元;
③当100<a≤120时,100﹣a<0,
由一次函数的性质可知,w随y的增大而减小,
则当y=7时,w取最大值,最大值为7(100﹣a)+6000=6700﹣7a,
即此时A型号彩电购进7台,B型号彩电购进13台才能使专卖店获得最大利润,最大利润是(6700﹣7a)元;
综上,当50≤a<100时,A型号彩电购进10台,B型号彩电购进10台才能使专卖店获得最大利润,最大利润是(7000﹣10a)元;当a=100时,按(2)的四种进货方案均可使专卖店获得最大利润,最大利润是6000元;当100<a≤120时,A型号彩电购进7台,B型号彩电购进13台才能使专卖店获得最大利润,最大利润是(6700﹣7a)元.
15.解:(1)由图象可得,
A地与B地的距离为4500m,
a=100×15=1500,
b=4500÷[(4500﹣1500)÷20]=30,
小明的实际速度为:4500÷30=150(m/min),
故答案为:4500,1500,30,150;
(2)由题意可得,
小亮的实际速度为:1500÷15=100(m/min),
当0≤x≤15时,s=4500﹣(150+100)x=﹣250x+4500;
当15<x≤20时,s=4500﹣(150+100)×15﹣150(x﹣15)=﹣150x+3000;
当20<x≤30时,s=150(x﹣20)=150x﹣3000;
当30<x≤60时,s=1500+100(x﹣30)=100x﹣1500;
综上,s与x的关系式为:s=;
图象如图1:
(3)如图2所示,
当y=2000时,﹣250x+4500=2000,
∴x=10,
100x﹣1500=2000,
∴x=35,
∴当两人之间的距离不大于2000m时,x的取值范围是10≤x≤35.
16.解:(1)填表如下:
C D 总计/t
A (240﹣x) (x﹣40) 200
B x (300﹣x) 300
总计/t 240 260 500
依题意得:20(240﹣x)+25(x﹣40)=15x+18(300﹣x)
解得:x=200
两个蔬菜基地调运蔬菜的运费相等时x的值为200.
(2)w与x之间的函数关系为:w=20(240﹣x)+25(x﹣40)+15x+18(300﹣x)=2x+9200
由题意得:
∴40≤x≤240
∵在w=2x+9200中,2>0
∴w随x的增大而增大
∴当x=40时,总运费最小
此时调运方案为:
(3)由题意得w=(2﹣m)x+9200
∴0<m<2,(2)中调运方案总费用最小;
m=2时,在40≤x≤240的前提下调运方案的总费用不变;
2<m<15时,x=240总费用最小,其调运方案如下:
17.解:(1)1500÷150=10(分钟),
10+5=15(分钟),
(3000﹣1500)÷(22.5﹣15)=200(米/分).
故答案为:10;15;200.
(2)BC段关系式为:y1=200x﹣1500,
OD段关系式为:y2=120x,
相遇时,即y1=y2,即120x=200x﹣1500
解得:x=18.75
此时:y1=y2=2250
距离图书馆:3000﹣2250=750(米)
答:小军在途中与爸爸第二次相遇时,距图书馆的距离是750米.
(3)当y1﹣y2=100时,解得x=20
当y2﹣y1=100时,解得x=17.5
答:爸爸自第二次出发至到达图书馆前,17.5分钟时和20分钟时与小军相距100米.
(2)旅客最多可免费携带30千克的行李.
18.解:(1)当0≤x≤10时,设y=kx﹣200,把(10,300)代入,得300=10x﹣200,
解得k=50,
∴y=50x﹣200;
w=80x﹣y=80x﹣(50x﹣200)=30x+200;
(2)当10≤x≤30时,设y=ax+b,把(30,1250),(10,250)代入,得
,
解得,
∴y=50x﹣250;
①当50x﹣200=280时,解得x=9.6,即960套,
w=30×9.6+200=488(百元)=48800(元);
②当50x﹣250=280时,解得x=10.6,即1060套,
w=30×10.6+200=568(百元)=56800(元).
答:若利润为28000元,售出了960套,需支付的成本费用是48800元;或售出了1060套,需支付的成本费用是56800元.
19.解:(1)400÷80+1+3=9,甲的速度=千米/小时
(2)由题意可得:E点坐标为(8,0),D(4,400)
设DE解析式y=kx+b
∴
解得:k=﹣100,b=800
∴解析式y=﹣100x+800
(3)根据题意可得:甲车到达B地前,两车恰好有一次相距80千米,
甲车在返回过程中,甲车超过乙车后到达A地的过程中,必有一次两车恰好有两次相距80千米,
即甲车在返回过程中,甲车追上乙车之前的过程中,两车相距不超过80千米,
∴80t<80
∴t<1
∴0<t<1
20.解:(1)由题意得,化简得,
即y与x之间的函数关系式为y=35﹣2x(15≥x≥10);
(2)由题意得:Q=5×0.6x+4 0.7y+3×0.8(30﹣x﹣y)=86﹣0.2x,
当x=10(台)时,Q最大,此时Q的最大值为84(万元);
即装运A、B、C货物的车辆分别为10台、15台、5台时,可以获得最大利润84万元;
(3)设此时外销活动的利润为Q′(万元),
由题意得:
Q′=5x(0.6+a)+4×0.7y+3×(30﹣x﹣y)(0.8+a)=86﹣0.2x+8ax﹣15a=(﹣0.2+8a)x+86﹣15a(15≥x≥10),
①当﹣0.2+8a=0时,有最大利润=86﹣15×=85.625(万元).
②当﹣0.2+8a>0时,即a>0.025,
故当a=0.03时,有最大利润=(﹣0.2+8a)15+86﹣15a=(83+105a)=83+105×0.03=86.15(万元)
③当﹣0.2+8a<0时,即a<﹣0.025,与0.01≤a≤0.03矛盾,故不成立,
故当a=0.03时,有最大利润=(﹣0.2+8a)15+86﹣15a=(83+105a)=83+105×0.03=86.15(万元),
即每吨售价提高0.03万元时,获得的最大利润为86.15万元.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
