西师大版 五年级下册数学 1.4 合数、质数 课件(共29张PPT)
文档属性
| 名称 | 西师大版 五年级下册数学 1.4 合数、质数 课件(共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-03 00:00:00 | ||
图片预览








文档简介
(共29张PPT)
西师大版数学五年级(下)
第4课时 合数、质数
倍数与因数
一
学习目标
1.认识和理解质数(素数)和合数的意义,并能正确
地判断质数和合数。
2.理解质因数的概念,明确质数和合数的关系,会用
短除法分解质因数。会把一个合数分解成几个质数
连乘积的形式。
3.在解决问题的过程中,能进行有条理的思考,对收
集的信息进行对比、归纳,感受数学文化的魅力。
【重点】
理解和掌握质数、合数的意义,认识质因数的概念。
【难点】
把一个合数分解成几个质数连乘积的形式。
复习导入
6 13 24 37
如果把下面的数分成两类,你打算怎样分?
可以分成奇数和偶数。6和24是偶数,13和17是奇数。
除了分成奇数和偶数,还可以怎样分?
让我们一起来探索吧!
探索新知
写出下面每个数的所有因数。
1
1的因数:
4的因数:
11的因数:
15的因数:
2的因数:
9的因数:
12的因数:
29的因数:
1、29
1、2、3、4、6、12
1、3、9
1、2
1、3、5、15
1、11
1、2、4
1
仔细观察,你有什么发现?
它们都有因数1,它们都有最大的因数,就是它本身。
1的因数:
4的因数:
11的因数:
15的因数:
2的因数:
9的因数:
12的因数:
29的因数:
1、29
1、2、3、4、6、12
1、3、9
1、2
1、3、5、15
1、11
1、2、4
1
1只有一个因数。
1的因数:
4的因数:
11的因数:
15的因数:
2的因数:
9的因数:
12的因数:
29的因数:
1、29
1、2、3、4、6、12
1、3、9
1、2
1、3、5、15
1、11
1、2、4
1
2,11,29它们的因数的个数是相同的,都只有2个因数。
4、9、12和15除了1和它本身这两个因数外,还有其他因数。
一个数的因数的个数是有限的。有的只有一个因数,有的有两个因数,有的有三个或三个以上的因数。一个数最小的因数都是1。最大的因数是它们本身。
如果要按一个数所含因数的个数,把上面的数分成3类的话,你认为可以怎样分?为什么?
只有1个因数
只有两个因数
有两个以上因数
2、11、29
4、9、12、15
1
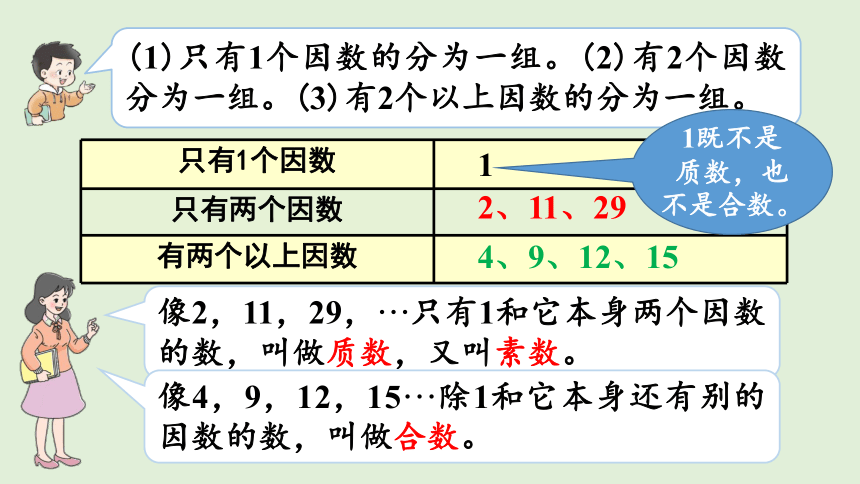
(1)只有1个因数的分为一组。(2)有2个因数分为一组。(3)有2个以上因数的分为一组。
像2,11,29,···只有1和它本身两个因数的数,叫做质数,又叫素数。
像4,9,12,15···除1和它本身还有别的因数的数,叫做合数。
1既不是质数,也不是合数。
一个数,如果只有1和它本身两个因数,这个数叫质数(或素数)。
一个数,如果除了1和它本身以外,还有其他因数,这个数叫合数。
1既不是质数,也不是合数。
你们知道如何来判断一个数是质数,还是合数了吗?
(1)如果一个数有且只有2个因数,就是1和它本身,这个数就是质数。
(2)如果这个数除了1和它本身这两个因 数外,还有第3个因数,这个数就是合数。
试 一 试
(教材第9页 “试一试”)
下面哪些数是质数?哪些数是合数?把它们分别填在相应的圈里。
3 5 6 7 10 13 25 72
3 5 7 13
6 10 25 72
质数
合数
除了1和它本身以外,还有其他因数。
只有1和它本身两个因数。
质数
合数
1
如果按因数的个数的多少,我们可以把非零的自然数分为三类:
非零自然数
质数
合数
1
把42写成质数相乘的形式。
42= 6×7
42= 2×3×7
2
42的因数:1、2、3、6、7、14、21、42。
方
法
一
可以先把42分解成两个数相乘的形式,再把其中的合数分解,直到所有因数都是质数为止。
探究把42写成质数相乘的形式
42
6
7
7是质数,不需要再分解。
6是合数,需要再进行分解。
2
3
42 = 6×7
6 = 2×3
2和3都是质数,不需要再分解了。
42=2×3×7
这种方法叫做树状图式分解法。
方
法
二
42=2×3×7
这种方法叫做短除法。
也可以先把42写在短除符号“ ”里,再用42的因数中的质数去除,要除以的质数写在短除号的左边,所得的商写在短除号的下面。
4 2
2
2 1
3
7
分解的数
商
除数
42 = 2×21
21 = 3×7
像这样,把一个合数写成几个质数连乘积的形式,叫做分解质因数。分解质因数,我们一般用短除法,用质数去除。
试 一 试
(教材第10页 “试一试”)
把8,30写成质数相乘的形式。
30=2×3×5
4
2
8
2
2
1 5
2
3 0
5
3
8=2×2×2
(教材第10页 “课堂活动”第1题 )
课堂练习
1.先划去2的倍数,再依次划去3、5、7的倍数
(2、3、5、7本身不划去)。
1 2 3 4 5 6 7 8 9 10
11 12 13 14 15 16 17 18 19 20
21 22 23 24 25 26 27 28 29 30
31 32 33 34 35 36 37 38 39 40
41 42 43 44 45 46 47 48 49 50
划去2的倍数,个位数是0 、2、4、6、8的数。
划去3的倍数,各数位上的数之和是3的倍数的数。
划去5的倍数,个位上的数是0或5的数。
划去7的倍数,还剩下49需要划去。
(教材第10页 “课堂活动”第2题 )
2.把上面没有划去的数由小到大写下来,看看它
们是什么数。
2 3 5 7 11 13 17 19 23 29 31 37 41 43 47
它们都是质数(素数)。
(教材第10页 “练习三”第1题 )
3.下面哪些数有因数2 哪些数有因数3 哪些数有
因数5
10 16 24 30 48 75 81
有因数2的是:10、16、24、30、48。
有因数3的是:21、30、48、75、81。
有因数5的是:10、30、75。
个位是0,2,4, 6,
8的数,是2的倍数。
3的倍数特征:一个数各个数位上的数字之和,是3的倍数。
个位是0或5的数,
是5的倍数。
(教材第10页 “练习三”第2题 )
4.下面哪些数是质数 把它们圈起来。
1 3 6 17 35 57 72 83
剩下的数都是合数吗
剩下的数不都是合数,因为1既不是质数,也不是合数。
质数:只有1和它本身两个因数。
合数:除了1和它本身以外,还有其他因数。
(教材第10页 “练习三”第8题 )
5.在1~100的自然数中,找出既是3的倍数也是5的
倍数的所有偶数和所有奇数,说说你是怎么找的。
既是3的倍数,又是5的倍数,那么必定是15的倍数。
所以这些数是:15 30 45 60 75 90
偶数是: 30 60 90
奇数是 :15 45 75
3的倍数有:3、6、9、15、18、···
5的倍数有:5、15、20、···
鸡蛋最多有多少个?
2个2个地数剩1个,
5个5个地数剩4个,
3个3个地数正好数完。
今天产的鸡蛋不超过40个。
鸡蛋最多有多少个?
用2、3、5的倍数特征解答。
最多不超过40个鸡蛋。
2个2个数还剩下1个,是奇数。
5个5个数还剩下4个,35是5的
倍数,35+4=39<40,是39个。
3个3个数刚好数完,是3的倍数。
39是3的倍数,所以是39个。
课堂小结
这节课你有什么收获?
这节课我们学习了质数(素数)和合数。
质数(素数)
只有1和它本身两个因数。
合数
除了1和它本身以外,还有其他因数。
1既不是质数,也不是因数。
这节课你有什么收获?
这节课我们还学习了质因数与分解质因数。
质因数
每个合数都可以写成几个质数相乘的形式,其中每个质数都是这个合数的质因数。
分解质因数
把一个合数用几个质数相乘的形式表示出来。
这节课你有什么收获?
这节课我们还学习了质因数与分解质因数。
分解质因数
树状图式分解法
短除法
02
01
课后作业
课后练习三。
相关练习。
西师大版数学五年级(下)
第4课时 合数、质数
倍数与因数
一
学习目标
1.认识和理解质数(素数)和合数的意义,并能正确
地判断质数和合数。
2.理解质因数的概念,明确质数和合数的关系,会用
短除法分解质因数。会把一个合数分解成几个质数
连乘积的形式。
3.在解决问题的过程中,能进行有条理的思考,对收
集的信息进行对比、归纳,感受数学文化的魅力。
【重点】
理解和掌握质数、合数的意义,认识质因数的概念。
【难点】
把一个合数分解成几个质数连乘积的形式。
复习导入
6 13 24 37
如果把下面的数分成两类,你打算怎样分?
可以分成奇数和偶数。6和24是偶数,13和17是奇数。
除了分成奇数和偶数,还可以怎样分?
让我们一起来探索吧!
探索新知
写出下面每个数的所有因数。
1
1的因数:
4的因数:
11的因数:
15的因数:
2的因数:
9的因数:
12的因数:
29的因数:
1、29
1、2、3、4、6、12
1、3、9
1、2
1、3、5、15
1、11
1、2、4
1
仔细观察,你有什么发现?
它们都有因数1,它们都有最大的因数,就是它本身。
1的因数:
4的因数:
11的因数:
15的因数:
2的因数:
9的因数:
12的因数:
29的因数:
1、29
1、2、3、4、6、12
1、3、9
1、2
1、3、5、15
1、11
1、2、4
1
1只有一个因数。
1的因数:
4的因数:
11的因数:
15的因数:
2的因数:
9的因数:
12的因数:
29的因数:
1、29
1、2、3、4、6、12
1、3、9
1、2
1、3、5、15
1、11
1、2、4
1
2,11,29它们的因数的个数是相同的,都只有2个因数。
4、9、12和15除了1和它本身这两个因数外,还有其他因数。
一个数的因数的个数是有限的。有的只有一个因数,有的有两个因数,有的有三个或三个以上的因数。一个数最小的因数都是1。最大的因数是它们本身。
如果要按一个数所含因数的个数,把上面的数分成3类的话,你认为可以怎样分?为什么?
只有1个因数
只有两个因数
有两个以上因数
2、11、29
4、9、12、15
1
(1)只有1个因数的分为一组。(2)有2个因数分为一组。(3)有2个以上因数的分为一组。
像2,11,29,···只有1和它本身两个因数的数,叫做质数,又叫素数。
像4,9,12,15···除1和它本身还有别的因数的数,叫做合数。
1既不是质数,也不是合数。
一个数,如果只有1和它本身两个因数,这个数叫质数(或素数)。
一个数,如果除了1和它本身以外,还有其他因数,这个数叫合数。
1既不是质数,也不是合数。
你们知道如何来判断一个数是质数,还是合数了吗?
(1)如果一个数有且只有2个因数,就是1和它本身,这个数就是质数。
(2)如果这个数除了1和它本身这两个因 数外,还有第3个因数,这个数就是合数。
试 一 试
(教材第9页 “试一试”)
下面哪些数是质数?哪些数是合数?把它们分别填在相应的圈里。
3 5 6 7 10 13 25 72
3 5 7 13
6 10 25 72
质数
合数
除了1和它本身以外,还有其他因数。
只有1和它本身两个因数。
质数
合数
1
如果按因数的个数的多少,我们可以把非零的自然数分为三类:
非零自然数
质数
合数
1
把42写成质数相乘的形式。
42= 6×7
42= 2×3×7
2
42的因数:1、2、3、6、7、14、21、42。
方
法
一
可以先把42分解成两个数相乘的形式,再把其中的合数分解,直到所有因数都是质数为止。
探究把42写成质数相乘的形式
42
6
7
7是质数,不需要再分解。
6是合数,需要再进行分解。
2
3
42 = 6×7
6 = 2×3
2和3都是质数,不需要再分解了。
42=2×3×7
这种方法叫做树状图式分解法。
方
法
二
42=2×3×7
这种方法叫做短除法。
也可以先把42写在短除符号“ ”里,再用42的因数中的质数去除,要除以的质数写在短除号的左边,所得的商写在短除号的下面。
4 2
2
2 1
3
7
分解的数
商
除数
42 = 2×21
21 = 3×7
像这样,把一个合数写成几个质数连乘积的形式,叫做分解质因数。分解质因数,我们一般用短除法,用质数去除。
试 一 试
(教材第10页 “试一试”)
把8,30写成质数相乘的形式。
30=2×3×5
4
2
8
2
2
1 5
2
3 0
5
3
8=2×2×2
(教材第10页 “课堂活动”第1题 )
课堂练习
1.先划去2的倍数,再依次划去3、5、7的倍数
(2、3、5、7本身不划去)。
1 2 3 4 5 6 7 8 9 10
11 12 13 14 15 16 17 18 19 20
21 22 23 24 25 26 27 28 29 30
31 32 33 34 35 36 37 38 39 40
41 42 43 44 45 46 47 48 49 50
划去2的倍数,个位数是0 、2、4、6、8的数。
划去3的倍数,各数位上的数之和是3的倍数的数。
划去5的倍数,个位上的数是0或5的数。
划去7的倍数,还剩下49需要划去。
(教材第10页 “课堂活动”第2题 )
2.把上面没有划去的数由小到大写下来,看看它
们是什么数。
2 3 5 7 11 13 17 19 23 29 31 37 41 43 47
它们都是质数(素数)。
(教材第10页 “练习三”第1题 )
3.下面哪些数有因数2 哪些数有因数3 哪些数有
因数5
10 16 24 30 48 75 81
有因数2的是:10、16、24、30、48。
有因数3的是:21、30、48、75、81。
有因数5的是:10、30、75。
个位是0,2,4, 6,
8的数,是2的倍数。
3的倍数特征:一个数各个数位上的数字之和,是3的倍数。
个位是0或5的数,
是5的倍数。
(教材第10页 “练习三”第2题 )
4.下面哪些数是质数 把它们圈起来。
1 3 6 17 35 57 72 83
剩下的数都是合数吗
剩下的数不都是合数,因为1既不是质数,也不是合数。
质数:只有1和它本身两个因数。
合数:除了1和它本身以外,还有其他因数。
(教材第10页 “练习三”第8题 )
5.在1~100的自然数中,找出既是3的倍数也是5的
倍数的所有偶数和所有奇数,说说你是怎么找的。
既是3的倍数,又是5的倍数,那么必定是15的倍数。
所以这些数是:15 30 45 60 75 90
偶数是: 30 60 90
奇数是 :15 45 75
3的倍数有:3、6、9、15、18、···
5的倍数有:5、15、20、···
鸡蛋最多有多少个?
2个2个地数剩1个,
5个5个地数剩4个,
3个3个地数正好数完。
今天产的鸡蛋不超过40个。
鸡蛋最多有多少个?
用2、3、5的倍数特征解答。
最多不超过40个鸡蛋。
2个2个数还剩下1个,是奇数。
5个5个数还剩下4个,35是5的
倍数,35+4=39<40,是39个。
3个3个数刚好数完,是3的倍数。
39是3的倍数,所以是39个。
课堂小结
这节课你有什么收获?
这节课我们学习了质数(素数)和合数。
质数(素数)
只有1和它本身两个因数。
合数
除了1和它本身以外,还有其他因数。
1既不是质数,也不是因数。
这节课你有什么收获?
这节课我们还学习了质因数与分解质因数。
质因数
每个合数都可以写成几个质数相乘的形式,其中每个质数都是这个合数的质因数。
分解质因数
把一个合数用几个质数相乘的形式表示出来。
这节课你有什么收获?
这节课我们还学习了质因数与分解质因数。
分解质因数
树状图式分解法
短除法
02
01
课后作业
课后练习三。
相关练习。
