西师大版 五年级下册数学 1.5 公因数 课件(共29张PPT)
文档属性
| 名称 | 西师大版 五年级下册数学 1.5 公因数 课件(共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-03 00:00:00 | ||
图片预览








文档简介
(共29张PPT)
西师大版数学五年级(下)
第5课时 公因数
倍数与因数
学习目标
1.探索学习公因数、最大公因数的概念,以及找两
个数的最大公因数的方法。经历找两个数的公因
数的过程,理解最大公因数的意义。
2.经历知识的整理与探究过程,增强归纳、概括等
数学能力,进一步发展数感。
3.进一步发展与同伴进行合作交流的意识和能力,
获得成功的体验。
【重点】
理解公因数和最大公因数的意义,会在集合圈中表示
两个数的因数和它们的公因数。
【难点】
掌握求两个数的最大公因数的方法。
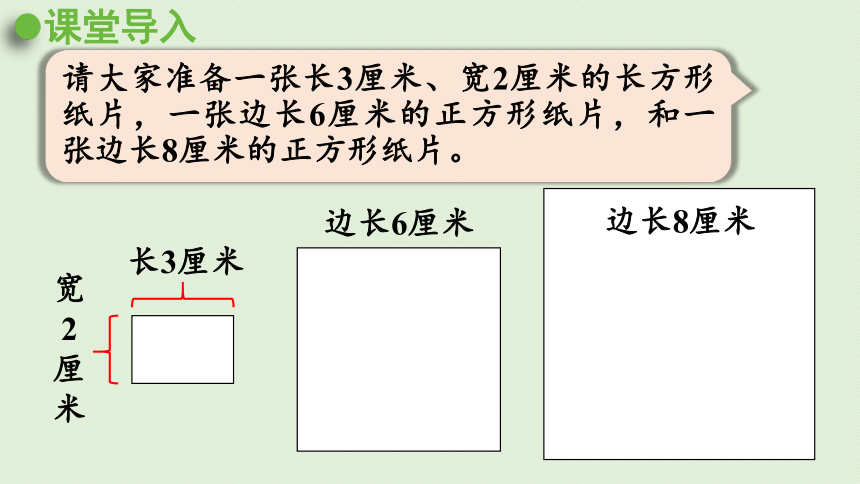
课堂导入
长3厘米
请大家准备一张长3厘米、宽2厘米的长方形纸片,一张边长6厘米的正方形纸片,和一张边长8厘米的正方形纸片。
边长6厘米
边长8厘米
宽
2
厘
米
用长3厘米、宽2厘米的长方形纸片分别铺边长6厘米、8厘米的正方形。
从中你发现了什么?
能铺满边长是6 cm的正方形,不能铺满边长是8 cm的正方形。
正方形的边长和长方形的长和宽有怎样的关系呢?
让我们一起来探索吧!
新知探究
1
一张长30 cm、宽12 cm的长方形纸,剪成大小相等的正方形且没有剩余,这个正方形的边长最大是多少厘米?
长30 cm
宽12 cm
剪成边长为1 cm的正方形。
长 30 cm
宽12 cm
边长1 cm
刚好剪完没有剩余。
剪成边长为2 cm的正方形。
长 30 cm
宽12 cm
边长2 cm
刚好剪完没有剩余。
剪成边长为3 cm的正方形。
长 30 cm
宽12 cm
边长3 cm
刚好剪完没有剩余。
剪成边长为4 cm的正方形。
长 30 cm
宽12 cm
边长4 cm
没有剪完有剩余。
剪成边长为5 cm的正方形。
长 30 cm
宽12 cm
边长5 cm
没有剪完有剩余。
剪成边长为6 cm的正方形。
长 30 cm
宽12 cm
边长6 cm
刚好剪完没有剩余。
当正方形边长是1 cm、2 cm、3 cm、6 cm时,这张长30 cm、宽12 cm的长方形刚好剪完且没有剩余,正方形边长最大是6 cm。
经过剪切你发现了什么?
这些正方形的边长和长方形的长和宽有什么关系呢?
30÷1=30 30÷2=15 30÷3=10 30÷6=5 12÷1=12 12÷2=6 12÷3=4 12÷6=2
用长方形的长和宽分别除以能刚好剪完的这些正方形的边长,你有什么发现?
要使剪出的正方形大小相等且没有剩余,正方形的边长必须既是12的因数,又是30的因数。也就是长方形长和宽的公有的因数,即公因数。
12的因数
30的因数
4
12
1
2
3
6
5
10
15
30
1
2
3
6
怎样来找这两个数的公因数呢?
小 提 示
分别找出这两个数的因数,再从这两个数的因数里找到它们的公因数。
12的因数
30的因数
4,
1,2, 3,
6 ,
1,2, 3, 6,
12
5,
10,15,30
12 和 30 公有的因数
12的因数
30的因数
4,12
1,2,
3,6
5,10, 15,30
1,2,3,6是12和30公有的因数,叫做它们的公因数。其中6是最大的一个公因数,叫做它们的最大公因数。
12 和 30 公有的因数
12的因数
30的因数
4,12
1,2,
3,6
5,10, 15,30
1 2
2
3
6
2
3 0
2
3
1 5
5
能不能把两个短除法合写成一个短除法?
······ 同时除以质因数 2
······ 同时除以质因数 3
······ 除到两个商只有公
因数1为止
12 和30 的最大公因数是2×3=6。
探究求12和30的最大公因数的方法
短除法
2和3既是12的因数,也是30的因数,即是12和30的公因数。
6 15
2 5
3
12 30
2
列举法
12的因数:
1,2,3,4,6,12。
30的因数:
1,2,3,5,6,10,15,30。
12和30的公因数:
12和30的最大公因数:
1,2,3,6。
6
6
你能找出 6 和 12 的公因数和最大公因数吗? 7 和 9 的最大公因数呢?
3 6
1 2
······ 同时除以质因数 2
······ 同时除以质因数 3
······ 除到两个商只有公因数1为止
2
3
6和 12 的最大公因数是:
2 ×3 = 6
6 12
2
试 一 试
(教材第12页“试一试”)
你能找出 6 和 12 的公因数和最大公因数吗? 7 和 9 的最大公因数呢?
7和9的最大公因数是:1
7 9
······ 同时除以质因数 1
1
7 9
试 一 试
(教材第12页“试一试”)
当两个数是质数时,它们的最大公因数为1。
16 20
2
2
8 10
4 5
16 和 20 的最大公因数是:
2 × 2 = 4
答:最多需要4个篮子。
把16个橘子、20个苹果按下面要求放到篮子里。最多需要多少个篮子?
每个篮子里橘子个数相同,苹果个数也相同。
议 一 议
(教材第13页“课堂活动”第1题)
每个篮子里既放
橘子又放苹果。
课堂练习
(教材第13页“练习四”第1题)
1.说出下面每组数的最大公因数。
6 和 8
15 和 30
8 和 9
18 和 30
最大公因数是:
1
6
2
15
2. 下面哪些分数的分子、分母有公因数2?哪些
有公因数3?哪些有公因数5?
5
6
10
15
12
21
8
10
20
30
6
18
12
18
有公因数2 :
有公因数3 :
有公因数5 :
10
15
12
21
6
18
6
18
8
10
12
18
12
18
20
30
20
30
想一想:2,3、5的倍数有哪些特征?
(教材第13页“练习4”第2题)
五(1)班有42人、五(2)班有48人参加植树活动。要求按班分组,如果两个班每组的人数必须相同,可以怎样分?每组最多有多少人?。
(教材第14页“练习4”第3题)
这道题是公因数和最大公因数知识的运用。
小提示
每组人数必须同样多,每组人数就应该是两班人数的公因数。
每组最多有多少人,应该是这些公因数中的最大公因数。
(教材第14页“练习4”第3题)
42 48
2
3
21 24
7 8
42 和 48 的最大公因数是:
2×3 = 6
42 和 48 的公因数是:1,2,3,6。
答:可以每2人、3人或6人一组, 每组最多有6人。
课堂小结
这节课你有什么收获?
这节课我们学习了公因数和最大公因数。
公因数
几个数公有的因数叫做这几个数的公因数。
最大公因数
其中最大的一个公因数,叫做它们的最大公因数。
这节课你有什么收获?
这节课我们还学习了怎样求两个数的最大公因数。
短除法
列举法
用两个数公有的质因数依次作除数去除这两个数,除到这两个数只有公因数1为止,然后再把所有的除数乘起来,所得的积就是这两个数的最大公因数。
先分别找出每个数的因数,然后找出它们的公因数,再从中找出最大的那个。
02
01
课后作业
课后练习四。
相关练习。
西师大版数学五年级(下)
第5课时 公因数
倍数与因数
学习目标
1.探索学习公因数、最大公因数的概念,以及找两
个数的最大公因数的方法。经历找两个数的公因
数的过程,理解最大公因数的意义。
2.经历知识的整理与探究过程,增强归纳、概括等
数学能力,进一步发展数感。
3.进一步发展与同伴进行合作交流的意识和能力,
获得成功的体验。
【重点】
理解公因数和最大公因数的意义,会在集合圈中表示
两个数的因数和它们的公因数。
【难点】
掌握求两个数的最大公因数的方法。
课堂导入
长3厘米
请大家准备一张长3厘米、宽2厘米的长方形纸片,一张边长6厘米的正方形纸片,和一张边长8厘米的正方形纸片。
边长6厘米
边长8厘米
宽
2
厘
米
用长3厘米、宽2厘米的长方形纸片分别铺边长6厘米、8厘米的正方形。
从中你发现了什么?
能铺满边长是6 cm的正方形,不能铺满边长是8 cm的正方形。
正方形的边长和长方形的长和宽有怎样的关系呢?
让我们一起来探索吧!
新知探究
1
一张长30 cm、宽12 cm的长方形纸,剪成大小相等的正方形且没有剩余,这个正方形的边长最大是多少厘米?
长30 cm
宽12 cm
剪成边长为1 cm的正方形。
长 30 cm
宽12 cm
边长1 cm
刚好剪完没有剩余。
剪成边长为2 cm的正方形。
长 30 cm
宽12 cm
边长2 cm
刚好剪完没有剩余。
剪成边长为3 cm的正方形。
长 30 cm
宽12 cm
边长3 cm
刚好剪完没有剩余。
剪成边长为4 cm的正方形。
长 30 cm
宽12 cm
边长4 cm
没有剪完有剩余。
剪成边长为5 cm的正方形。
长 30 cm
宽12 cm
边长5 cm
没有剪完有剩余。
剪成边长为6 cm的正方形。
长 30 cm
宽12 cm
边长6 cm
刚好剪完没有剩余。
当正方形边长是1 cm、2 cm、3 cm、6 cm时,这张长30 cm、宽12 cm的长方形刚好剪完且没有剩余,正方形边长最大是6 cm。
经过剪切你发现了什么?
这些正方形的边长和长方形的长和宽有什么关系呢?
30÷1=30 30÷2=15 30÷3=10 30÷6=5 12÷1=12 12÷2=6 12÷3=4 12÷6=2
用长方形的长和宽分别除以能刚好剪完的这些正方形的边长,你有什么发现?
要使剪出的正方形大小相等且没有剩余,正方形的边长必须既是12的因数,又是30的因数。也就是长方形长和宽的公有的因数,即公因数。
12的因数
30的因数
4
12
1
2
3
6
5
10
15
30
1
2
3
6
怎样来找这两个数的公因数呢?
小 提 示
分别找出这两个数的因数,再从这两个数的因数里找到它们的公因数。
12的因数
30的因数
4,
1,2, 3,
6 ,
1,2, 3, 6,
12
5,
10,15,30
12 和 30 公有的因数
12的因数
30的因数
4,12
1,2,
3,6
5,10, 15,30
1,2,3,6是12和30公有的因数,叫做它们的公因数。其中6是最大的一个公因数,叫做它们的最大公因数。
12 和 30 公有的因数
12的因数
30的因数
4,12
1,2,
3,6
5,10, 15,30
1 2
2
3
6
2
3 0
2
3
1 5
5
能不能把两个短除法合写成一个短除法?
······ 同时除以质因数 2
······ 同时除以质因数 3
······ 除到两个商只有公
因数1为止
12 和30 的最大公因数是2×3=6。
探究求12和30的最大公因数的方法
短除法
2和3既是12的因数,也是30的因数,即是12和30的公因数。
6 15
2 5
3
12 30
2
列举法
12的因数:
1,2,3,4,6,12。
30的因数:
1,2,3,5,6,10,15,30。
12和30的公因数:
12和30的最大公因数:
1,2,3,6。
6
6
你能找出 6 和 12 的公因数和最大公因数吗? 7 和 9 的最大公因数呢?
3 6
1 2
······ 同时除以质因数 2
······ 同时除以质因数 3
······ 除到两个商只有公因数1为止
2
3
6和 12 的最大公因数是:
2 ×3 = 6
6 12
2
试 一 试
(教材第12页“试一试”)
你能找出 6 和 12 的公因数和最大公因数吗? 7 和 9 的最大公因数呢?
7和9的最大公因数是:1
7 9
······ 同时除以质因数 1
1
7 9
试 一 试
(教材第12页“试一试”)
当两个数是质数时,它们的最大公因数为1。
16 20
2
2
8 10
4 5
16 和 20 的最大公因数是:
2 × 2 = 4
答:最多需要4个篮子。
把16个橘子、20个苹果按下面要求放到篮子里。最多需要多少个篮子?
每个篮子里橘子个数相同,苹果个数也相同。
议 一 议
(教材第13页“课堂活动”第1题)
每个篮子里既放
橘子又放苹果。
课堂练习
(教材第13页“练习四”第1题)
1.说出下面每组数的最大公因数。
6 和 8
15 和 30
8 和 9
18 和 30
最大公因数是:
1
6
2
15
2. 下面哪些分数的分子、分母有公因数2?哪些
有公因数3?哪些有公因数5?
5
6
10
15
12
21
8
10
20
30
6
18
12
18
有公因数2 :
有公因数3 :
有公因数5 :
10
15
12
21
6
18
6
18
8
10
12
18
12
18
20
30
20
30
想一想:2,3、5的倍数有哪些特征?
(教材第13页“练习4”第2题)
五(1)班有42人、五(2)班有48人参加植树活动。要求按班分组,如果两个班每组的人数必须相同,可以怎样分?每组最多有多少人?。
(教材第14页“练习4”第3题)
这道题是公因数和最大公因数知识的运用。
小提示
每组人数必须同样多,每组人数就应该是两班人数的公因数。
每组最多有多少人,应该是这些公因数中的最大公因数。
(教材第14页“练习4”第3题)
42 48
2
3
21 24
7 8
42 和 48 的最大公因数是:
2×3 = 6
42 和 48 的公因数是:1,2,3,6。
答:可以每2人、3人或6人一组, 每组最多有6人。
课堂小结
这节课你有什么收获?
这节课我们学习了公因数和最大公因数。
公因数
几个数公有的因数叫做这几个数的公因数。
最大公因数
其中最大的一个公因数,叫做它们的最大公因数。
这节课你有什么收获?
这节课我们还学习了怎样求两个数的最大公因数。
短除法
列举法
用两个数公有的质因数依次作除数去除这两个数,除到这两个数只有公因数1为止,然后再把所有的除数乘起来,所得的积就是这两个数的最大公因数。
先分别找出每个数的因数,然后找出它们的公因数,再从中找出最大的那个。
02
01
课后作业
课后练习四。
相关练习。
