西师大版 五年级下册数学 1.7 倍数与因数 整理与复习 课件(共38张PPT)
文档属性
| 名称 | 西师大版 五年级下册数学 1.7 倍数与因数 整理与复习 课件(共38张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 7.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-03 10:09:33 | ||
图片预览










文档简介
(共38张PPT)
西师大版数学五年级(下)
第7课时 整理与复习
倍数与因数
通过复习,进一步巩固倍数、因数、质数、合数等概念及其相互间的关系,掌握2、3、5的倍数特征。
在讨论交流的过程中,归纳总结本单元的主要知识点,加强对知识的系统把握能力。
能灵活运用有关倍数和因数的知识来解决生活中的实际问题。
学习目标
【重点】
能综合运用所学的知识解决实际问题。
【难点】
能用网络图整理所学的知识,并理解有
关概念之间的联系和区别。
知识梳理
通过本单元的学习,你有什么收获?
认识了倍数和因数,知道倍数和因数是相互的,不能单独存在。
认识了质数和合数。
认识了公因数和公倍数。
一起来回顾一下第一单元学过的知识吧!
还学习了质数、合数、公因数和公倍数。
本单元内容是
在非零自然数范围内讨论的。
它们之间有哪些联系和区别呢?
学习了倍数、因数。
你是怎样学习这些知识的?知识之间有哪些联系和区别?
认识了倍数和因数,知道倍数和因数是相互依存的。
例如:2×7=14 16÷2=8
14是2和7的倍数,2和7是14的因数。
16是2和8的倍数,2和8是16的因数。
找一个数的倍数和因数,可以用乘法来找,也可以用除法来找。
倍数和因数
倍数
因数
(非零自然数)
本单元我们学习的知识,哪些与倍数有关?
个位上是0, 2, 4, 6, 8的数是2的倍数。
自然数中,是2的倍数的数叫偶数(0也是偶数),
不是2的倍数的数叫奇数。
2的倍数特征:
要点回顾
知识点1:2,3 ,5的倍数特征
一个数各个数位上的数字之和是3的倍数,这个数就是3的倍数。。
3的倍数特征:
1 2 3 4 5 6 7 8 9 10
11 12 13 14 15 16 17 18 19 20
21 22 23 24 25 26 27 28 29 30
31 32 33 34 35 36 37 38 39 40
41 42 43 44 45 46 47 48 49 50
51 52 53 54 55 56 57 58 59 60
61 62 63 64 65 66 67 68 69 70
71 72 73 74 75 76 77 78 79 80
81 82 83 84 85 86 87 88 89 90
91 92 93 94 95 96 97 98 99 100
1 2 3 4 5 6 7 8 9 10
11 12 13 14 15 16 17 18 19 20
21 22 23 24 25 26 27 28 29 30
31 32 33 34 35 36 37 38 39 40
41 42 43 44 45 46 47 48 49 50
51 52 53 54 55 56 57 58 59 60
61 62 63 64 65 66 67 68 69 70
71 72 73 74 75 76 77 78 79 80
81 82 83 84 85 86 87 88 89 90
91 92 93 94 95 96 97 98 99 100
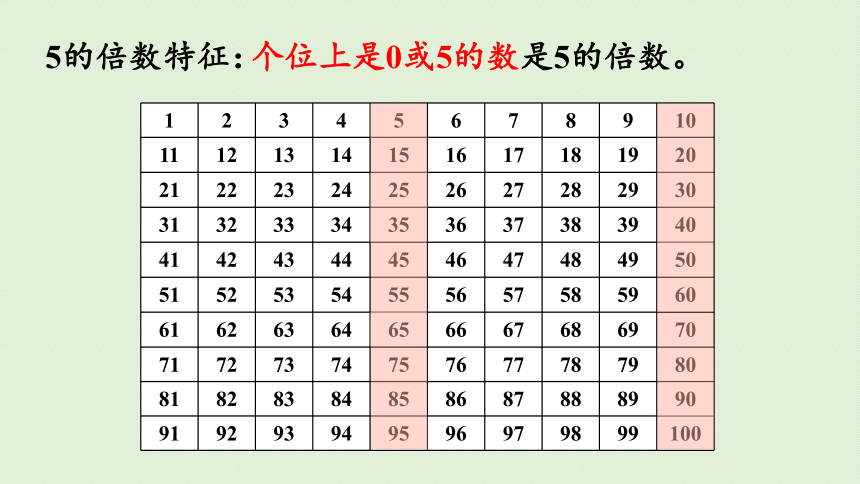
个位上是0或5的数是5的倍数。
5的倍数特征:
求两个数的最小公倍数的方法
列举法。也就是先各自找出两个数
的倍数,再从各自的倍数中找出两
个数的公倍数,最后找出两个数的
最小公倍数。
求两个数的最小公倍数的方法
分解质因数法。先把这两个数分解
质因数,再把两个数共有的质因数
(取一次)和各自独有的质因数(全
部取)相乘,所得的积就是这两个
数的最小公倍数。
求两个数的最小公倍数的方法
短除法。用它们公有的质因数去除
这两个数,一直除到商只有公因数1
为止,然后把所有的除数与商连乘,
所得的积就是它们的最小公倍数。
倍数有关知识总结
倍数和因数
倍数
2的倍数特征
3的倍数特征
5的倍数特征
公倍数
因数
最小公倍数
偶数(包含0)
奇数
本单元我们学习的知识,哪些与因数有关?
1既不是质数,也不是合数。
只有1和它本身两个因数的数,叫做质数(或素数)。
除1和它本身外还有别的因数的数,叫做合数。
质数:
合数:
知识点2:合数、质数
最小的质数是2,最小的合数是4。
求两个数的最大公因数的方法
列举法。也就是先各自找出两个数
的因数,再找它们的公因数,最后
找出最大的公因数。
求两个数的最大公因数的方法
分解质因数法。先把这两个数分解质因数,再把两个数公有的质因数(取一次)相乘,所得的积就是这两个数的最大公因数。
求两个数的最大公因数的方法
短除法。用它们公有的质因数去除这两个数,一直除到商只有公因数1为止,然后把所有的除数相乘,所得的积就是它们的最大公因数。
因数有关知识总结
倍数和因数
倍数
2的倍数特征
3的倍数特征
5的倍数特征
公倍数
因数
最小公倍数
偶数(包含0)
奇数
合数
质数
1
公因数
最大公因数
1.填一填,并说一说填的理由。
45 24 25 60 90 38 21
(教材第15页“整理与复习”第2题)
2的倍数
3的倍数
5的倍数
我们可以根据2,3,5的倍数特征来填。
填个位是
0, 2, 4, 6, 8
的数。
填所有数位上数字的和是3的倍数的数。
填个位是0或5的数。
24,60
90,38
45,24,60
90,21
45,25
60,90
24, 38
45, 25
2,5的公倍数
3,5的公倍数
60, 90
哪些数是2,5的公倍数?
当个位上数字是 0 时,这个数就是 2, 5 的公倍数。
(教材第15页“议一议”)
议 一 议
2的倍数
3的倍数
5的倍数
3的倍数
24, 38
45, 25
2,5的公倍数
3,5的公倍数
60, 90
45, 60,
90
24, 21
25
(教材第15页“议一议”)
议 一 议
2的倍数
3的倍数
5的倍数
3的倍数
个位上的数字是0或5,而且各数位上的数字之和是3的倍数,这个数就是3,5的公倍数。
哪些数是3,5的公倍数?
6和18的最大公因数: 2×3=6
11和13的最大公因数:1
8和36的最大公因数:2×2=4
2.(1)求下面每组数的最大公因数。
6和18
11和13
8和36
6=2×3
18=2×3×3
11和13都是质数
8=2×2×2
36=2×2×3×3
列举法
当两个数中较大的数是较小的数的倍数时,较小的数是这两个数的最大公因数。
(教材第15页“整理与复习”第3题)
2.(1)求下面每组数的最大公因数。
6和18
11和13
8和36
短除法
(教材第15页“整理与复习”第3题)
4 18
2
3
2
1 3
11 13
1
11 13
8 36
2
2 9
6 18
3 9
6和18的最大公因数: 2×3=6
11和13的最大公因数:1
8和36的最大公因数:2×2=4
2.(2)求下面每组数的最小公倍数。
3和7
2和6
4和10
(教材第15页“整理与复习”第3题)
3 7
3 7
1
3和7的最小公倍数是1×3×7=21。
1 3
2
2和6的最小公倍数是2×1×3=6。
2 5
2
4和10的最小公倍数是2×2×5=20。
2 6
4 10
课堂练习
(教材第16页“练习五”第1题)
1.填空。
(1)5×7=35, 7和( )是35的因数,35和7是
7和( )的倍数 。
5
5
(2)找一找,填一填。
1 3 12 9 6 18 60 27
9的因数
9的倍数
1
3
12
9
6
60
27
18
9
9
(教材第16页“练习五”第1题)
1.填空。
提示:满足题中条件的最大两位数,个位上
的数字一定是0或5,且十位上的数字
加上 0 或 5 必须是 3 的倍数,那就只
有 1,3,4,6,7,9。
(3)同时是3,5的倍数的数中,最大的两位数
是( )。
90
2.下面哪些数是奇数,哪些数是偶数。
55 24 100 27 12 101 99
(教材第16页“练习5”第2题)
自然数中,不是2的倍数的数叫奇数。个位是1, 3, 5, 7, 9的数都是奇数。
自然数中,是2的倍数的数叫偶数。个位是0, 2, 4, 6, 8的数都是偶数。
奇数
偶数
2.下面哪些数是奇数,哪些数是偶数。
55 24 100 27 12 101 99
55, 27,
99, 101
24, 12, 100
(教材第16页“练习5”第2题)
3. 23路公交车每5分发车一次,6路公交车
每8分发车一次,这两路车同时发车后,
至少再过多少时间又同时发车?
23路
6路
同时发车
5分
8分
1
2
8
5
1
第二次同时发车
5×8= 40
8×5= 40
(教材第16页“练习5”第3题)
3
2
3
4
5
6
7
4
求至少多少时间又同时发车,就是求5和8的最小公倍数。
(教材第16页“练习5”第3题)
5和8的最小公倍数:
1×5×8= 40
短除法
5 8
5 8
1
答:至少再过40分又同时发车。
4.猜电话号码。
(教材第16页“练习5”第4题)
这个电话号码是在什么情况下使用?
这个电话号码是3位数
百位上的数既不是质数,也不是合数。
这个数是1。
十位上的数是所有非零自然数的因数。
这个数是1。
个位上的数既是奇数,又是合数。
9
1
1
这个号码是发生火警时使用的。
(教材第16页“练习5”第4题)
1、3、5、7、
9是奇数,9是奇数又是
合数。
拓展阅读
陈景润与哥德巴赫猜想
陈景润(1933-1996)是我国现代享誉世界的著名数学家。他在中学就对哥德巴赫猜想产生了浓厚的兴趣。
哥德巴赫是德国数学家,在200多年前提出了一个猜想:每个大于4的偶数是两个奇质数的和。
陈景润在极其艰苦的条件下,花费了10多年时间,来证明这一猜想,仅演算的稿纸就有6麻袋之多。
1966年陈景润终于取得了令人瞩目的成就,他的证明在国际上被誉为“陈氏定理”。这距摘取哥德巴赫猜想这项数学皇冠上的明珠只是一步之遥。
02
01
课后作业
课后练习五。
相关练习。
西师大版数学五年级(下)
第7课时 整理与复习
倍数与因数
通过复习,进一步巩固倍数、因数、质数、合数等概念及其相互间的关系,掌握2、3、5的倍数特征。
在讨论交流的过程中,归纳总结本单元的主要知识点,加强对知识的系统把握能力。
能灵活运用有关倍数和因数的知识来解决生活中的实际问题。
学习目标
【重点】
能综合运用所学的知识解决实际问题。
【难点】
能用网络图整理所学的知识,并理解有
关概念之间的联系和区别。
知识梳理
通过本单元的学习,你有什么收获?
认识了倍数和因数,知道倍数和因数是相互的,不能单独存在。
认识了质数和合数。
认识了公因数和公倍数。
一起来回顾一下第一单元学过的知识吧!
还学习了质数、合数、公因数和公倍数。
本单元内容是
在非零自然数范围内讨论的。
它们之间有哪些联系和区别呢?
学习了倍数、因数。
你是怎样学习这些知识的?知识之间有哪些联系和区别?
认识了倍数和因数,知道倍数和因数是相互依存的。
例如:2×7=14 16÷2=8
14是2和7的倍数,2和7是14的因数。
16是2和8的倍数,2和8是16的因数。
找一个数的倍数和因数,可以用乘法来找,也可以用除法来找。
倍数和因数
倍数
因数
(非零自然数)
本单元我们学习的知识,哪些与倍数有关?
个位上是0, 2, 4, 6, 8的数是2的倍数。
自然数中,是2的倍数的数叫偶数(0也是偶数),
不是2的倍数的数叫奇数。
2的倍数特征:
要点回顾
知识点1:2,3 ,5的倍数特征
一个数各个数位上的数字之和是3的倍数,这个数就是3的倍数。。
3的倍数特征:
1 2 3 4 5 6 7 8 9 10
11 12 13 14 15 16 17 18 19 20
21 22 23 24 25 26 27 28 29 30
31 32 33 34 35 36 37 38 39 40
41 42 43 44 45 46 47 48 49 50
51 52 53 54 55 56 57 58 59 60
61 62 63 64 65 66 67 68 69 70
71 72 73 74 75 76 77 78 79 80
81 82 83 84 85 86 87 88 89 90
91 92 93 94 95 96 97 98 99 100
1 2 3 4 5 6 7 8 9 10
11 12 13 14 15 16 17 18 19 20
21 22 23 24 25 26 27 28 29 30
31 32 33 34 35 36 37 38 39 40
41 42 43 44 45 46 47 48 49 50
51 52 53 54 55 56 57 58 59 60
61 62 63 64 65 66 67 68 69 70
71 72 73 74 75 76 77 78 79 80
81 82 83 84 85 86 87 88 89 90
91 92 93 94 95 96 97 98 99 100
个位上是0或5的数是5的倍数。
5的倍数特征:
求两个数的最小公倍数的方法
列举法。也就是先各自找出两个数
的倍数,再从各自的倍数中找出两
个数的公倍数,最后找出两个数的
最小公倍数。
求两个数的最小公倍数的方法
分解质因数法。先把这两个数分解
质因数,再把两个数共有的质因数
(取一次)和各自独有的质因数(全
部取)相乘,所得的积就是这两个
数的最小公倍数。
求两个数的最小公倍数的方法
短除法。用它们公有的质因数去除
这两个数,一直除到商只有公因数1
为止,然后把所有的除数与商连乘,
所得的积就是它们的最小公倍数。
倍数有关知识总结
倍数和因数
倍数
2的倍数特征
3的倍数特征
5的倍数特征
公倍数
因数
最小公倍数
偶数(包含0)
奇数
本单元我们学习的知识,哪些与因数有关?
1既不是质数,也不是合数。
只有1和它本身两个因数的数,叫做质数(或素数)。
除1和它本身外还有别的因数的数,叫做合数。
质数:
合数:
知识点2:合数、质数
最小的质数是2,最小的合数是4。
求两个数的最大公因数的方法
列举法。也就是先各自找出两个数
的因数,再找它们的公因数,最后
找出最大的公因数。
求两个数的最大公因数的方法
分解质因数法。先把这两个数分解质因数,再把两个数公有的质因数(取一次)相乘,所得的积就是这两个数的最大公因数。
求两个数的最大公因数的方法
短除法。用它们公有的质因数去除这两个数,一直除到商只有公因数1为止,然后把所有的除数相乘,所得的积就是它们的最大公因数。
因数有关知识总结
倍数和因数
倍数
2的倍数特征
3的倍数特征
5的倍数特征
公倍数
因数
最小公倍数
偶数(包含0)
奇数
合数
质数
1
公因数
最大公因数
1.填一填,并说一说填的理由。
45 24 25 60 90 38 21
(教材第15页“整理与复习”第2题)
2的倍数
3的倍数
5的倍数
我们可以根据2,3,5的倍数特征来填。
填个位是
0, 2, 4, 6, 8
的数。
填所有数位上数字的和是3的倍数的数。
填个位是0或5的数。
24,60
90,38
45,24,60
90,21
45,25
60,90
24, 38
45, 25
2,5的公倍数
3,5的公倍数
60, 90
哪些数是2,5的公倍数?
当个位上数字是 0 时,这个数就是 2, 5 的公倍数。
(教材第15页“议一议”)
议 一 议
2的倍数
3的倍数
5的倍数
3的倍数
24, 38
45, 25
2,5的公倍数
3,5的公倍数
60, 90
45, 60,
90
24, 21
25
(教材第15页“议一议”)
议 一 议
2的倍数
3的倍数
5的倍数
3的倍数
个位上的数字是0或5,而且各数位上的数字之和是3的倍数,这个数就是3,5的公倍数。
哪些数是3,5的公倍数?
6和18的最大公因数: 2×3=6
11和13的最大公因数:1
8和36的最大公因数:2×2=4
2.(1)求下面每组数的最大公因数。
6和18
11和13
8和36
6=2×3
18=2×3×3
11和13都是质数
8=2×2×2
36=2×2×3×3
列举法
当两个数中较大的数是较小的数的倍数时,较小的数是这两个数的最大公因数。
(教材第15页“整理与复习”第3题)
2.(1)求下面每组数的最大公因数。
6和18
11和13
8和36
短除法
(教材第15页“整理与复习”第3题)
4 18
2
3
2
1 3
11 13
1
11 13
8 36
2
2 9
6 18
3 9
6和18的最大公因数: 2×3=6
11和13的最大公因数:1
8和36的最大公因数:2×2=4
2.(2)求下面每组数的最小公倍数。
3和7
2和6
4和10
(教材第15页“整理与复习”第3题)
3 7
3 7
1
3和7的最小公倍数是1×3×7=21。
1 3
2
2和6的最小公倍数是2×1×3=6。
2 5
2
4和10的最小公倍数是2×2×5=20。
2 6
4 10
课堂练习
(教材第16页“练习五”第1题)
1.填空。
(1)5×7=35, 7和( )是35的因数,35和7是
7和( )的倍数 。
5
5
(2)找一找,填一填。
1 3 12 9 6 18 60 27
9的因数
9的倍数
1
3
12
9
6
60
27
18
9
9
(教材第16页“练习五”第1题)
1.填空。
提示:满足题中条件的最大两位数,个位上
的数字一定是0或5,且十位上的数字
加上 0 或 5 必须是 3 的倍数,那就只
有 1,3,4,6,7,9。
(3)同时是3,5的倍数的数中,最大的两位数
是( )。
90
2.下面哪些数是奇数,哪些数是偶数。
55 24 100 27 12 101 99
(教材第16页“练习5”第2题)
自然数中,不是2的倍数的数叫奇数。个位是1, 3, 5, 7, 9的数都是奇数。
自然数中,是2的倍数的数叫偶数。个位是0, 2, 4, 6, 8的数都是偶数。
奇数
偶数
2.下面哪些数是奇数,哪些数是偶数。
55 24 100 27 12 101 99
55, 27,
99, 101
24, 12, 100
(教材第16页“练习5”第2题)
3. 23路公交车每5分发车一次,6路公交车
每8分发车一次,这两路车同时发车后,
至少再过多少时间又同时发车?
23路
6路
同时发车
5分
8分
1
2
8
5
1
第二次同时发车
5×8= 40
8×5= 40
(教材第16页“练习5”第3题)
3
2
3
4
5
6
7
4
求至少多少时间又同时发车,就是求5和8的最小公倍数。
(教材第16页“练习5”第3题)
5和8的最小公倍数:
1×5×8= 40
短除法
5 8
5 8
1
答:至少再过40分又同时发车。
4.猜电话号码。
(教材第16页“练习5”第4题)
这个电话号码是在什么情况下使用?
这个电话号码是3位数
百位上的数既不是质数,也不是合数。
这个数是1。
十位上的数是所有非零自然数的因数。
这个数是1。
个位上的数既是奇数,又是合数。
9
1
1
这个号码是发生火警时使用的。
(教材第16页“练习5”第4题)
1、3、5、7、
9是奇数,9是奇数又是
合数。
拓展阅读
陈景润与哥德巴赫猜想
陈景润(1933-1996)是我国现代享誉世界的著名数学家。他在中学就对哥德巴赫猜想产生了浓厚的兴趣。
哥德巴赫是德国数学家,在200多年前提出了一个猜想:每个大于4的偶数是两个奇质数的和。
陈景润在极其艰苦的条件下,花费了10多年时间,来证明这一猜想,仅演算的稿纸就有6麻袋之多。
1966年陈景润终于取得了令人瞩目的成就,他的证明在国际上被誉为“陈氏定理”。这距摘取哥德巴赫猜想这项数学皇冠上的明珠只是一步之遥。
02
01
课后作业
课后练习五。
相关练习。
