西师大版数学五年级下册2.8 约分 课件(27张ppt)
文档属性
| 名称 | 西师大版数学五年级下册2.8 约分 课件(27张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-03 00:00:00 | ||
图片预览







文档简介
(共27张PPT)
西师大版数学五年级(下)
第8课时 约分
分 数
二
1.知道最简分数的含义,理解什么是约分,掌握约分的方法并能用这个方法正确地约分。并能进行异分母分母的大小比较。
2.经历知识的形成过程,使学生理解约分与最简分数,的大小比较的方法。
3.在探究约分的过程中,获得成其功的体验和学习的乐趣。
学习目标
【重点】
理解约分和通分的意义,能正确的进行约分和通分练习。
【难点】
学会根据实际需要进行约分和通分,
熟练地掌握约分和通分的方法。
课堂导入
折一折,涂一涂。
(1)拿出方形纸,把它对折一次,然后
把其中的一份涂上颜色。
(2)把这张纸对折两次、三次。
(3)分别用分数表示出涂色部分的面积。
它们之间有怎样的一种关系?
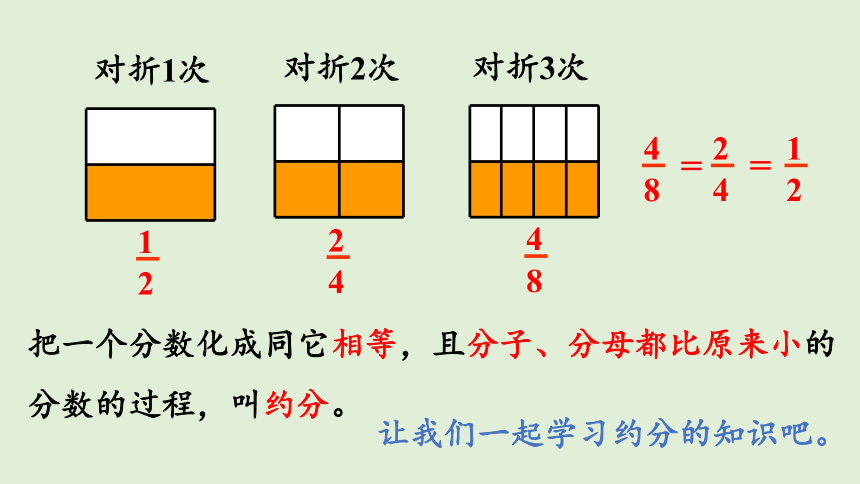
对折1次
对折2次
对折3次
对折1次
对折2次
对折3次
1
2
2
4
4
8
1
2
2
4
4
8
=
=
把一个分数化成同它相等,且分子、分母都比原来小的分数的过程,叫约分。
让我们一起学习约分的知识吧。
新知探究
1
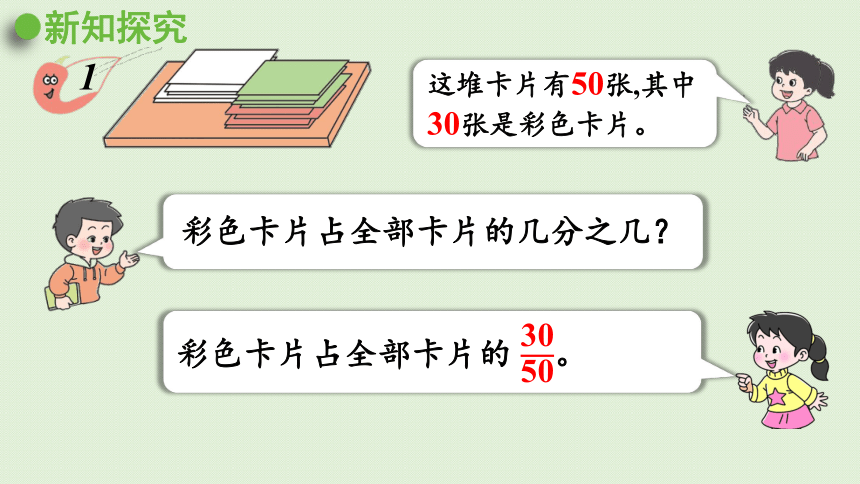
彩色卡片占全部卡片的几分之几?
这堆卡片有50张,其中30张是彩色卡片。
彩色卡片占全部卡片的 。
你能把 化成分子、分母都比较小的分数吗?
30
50
用分数的基本性质,把分子和分母同时缩小相同的倍数。
=
15
25
30
50
30÷2
50÷2
=
=
6
10
30
50
30÷5
50÷5
=
=
30
50
30÷10
50÷10
3
5
=
30
50
=
=
15
25
6
10
=
3
5
从中你发现了什么?
它们的分子和分母越来越小。
像这样,把一个分数化成同它相等,且分子分母都比较小的分数的过程,叫做约分。
30
50
还有更简便的方法。
25
15
5
3
3
5
=
分子、分母同时除以公因数2,再除以公因数5。
方法一
30
50
5
3
3
5
=
分子、分母同时除以它们的最大公因数10。
方法二
这两种方法有哪些相同的地方,有哪些不同的地方?
都是把化简成,所以都是约分。
约分的过程不同,方法一约分了两次,方法二是约分了一次。
你能具体地解释一下,这两种不同的约分的过程吗?
方法一是用分子、分母的公因数一次一次地去化简。
方法二是用分子、分母的最大公因数一次化简。
把 , , 化成最简分数。
试 一 试
(教材第30页“试一试”)
18
24
6
18
10
35
18
24
4
3
3
4
=
分子、分母同时除以它们的最大公因数6。
6
18
3
1
1
3
=
(教材第30页“试一试”)
10
35
分子、分母同时除以它们的最大公因数5。
2
7
2
7
=
课堂练习
(教材第30页“课堂活动” )
不是最简分数,它的分子、分母有公因数2,3,6。
一个同学任意写出一个分数,另一个同学判断这个分数是不是最简分数,并说出理由。
6
18
判断一个分数是不是最简分数时,我们应用到了哪些知识呢?
应用到了分数的基本性质、公因数、最大公因数等知识。
2.化简。
12
27
10
25
先找出分子和分母的最大公因数。
最大公因数3
4
9
2
5
=
2
5
4
9
=
最大公因数5
(教材第32页“练习九”第1题)
28
42
24
30
30
45
4
5
最大公因数6
4
5
=
最大公因数15
2
3
2
3
=
最大公因数14
2
3
2
3
=
3.客车的辆数是货车的几分之几?
(教材第32页“练习九”第2题)
停车场有42辆货车,36辆客车,8辆小轿车。
3.客车的辆数是货车的几分之几?
(教材第32页“练习九”第2题)
36
42
6
7
=
答:客车的辆数是货车的 。
6
7
1.货车的辆数是客车的几分之几?
2.小轿车的辆数是客车的几分之几?
3.客车的辆数是小轿车的几分之几?
4.小轿车的辆数是货车的几分之几?
5.货车的辆数是小轿车的几分之几?
你还可以提出哪些数学问题?
1. 2. 3. 4. 5.
7
6
21
4
4
21
9
2
2
9
这节课你有什么收获?
课堂小结
把一个分数化成同它相等,且分子分母都比较小的分数的过程,叫做约分。
分子和分母只有公因数1的分数叫做最简分数。
这节课你有什么收获?
约分的方法
(1)逐次约分法,用分子、分母同时除以它们的公因数,一直到分子、分母只有公因数1为止。
(2)一次约分法,用分子和分母同时除以它们的最大公因数。
02
01
课后作业
课后练习九。
作业课件中的相关练习。
西师大版数学五年级(下)
第8课时 约分
分 数
二
1.知道最简分数的含义,理解什么是约分,掌握约分的方法并能用这个方法正确地约分。并能进行异分母分母的大小比较。
2.经历知识的形成过程,使学生理解约分与最简分数,的大小比较的方法。
3.在探究约分的过程中,获得成其功的体验和学习的乐趣。
学习目标
【重点】
理解约分和通分的意义,能正确的进行约分和通分练习。
【难点】
学会根据实际需要进行约分和通分,
熟练地掌握约分和通分的方法。
课堂导入
折一折,涂一涂。
(1)拿出方形纸,把它对折一次,然后
把其中的一份涂上颜色。
(2)把这张纸对折两次、三次。
(3)分别用分数表示出涂色部分的面积。
它们之间有怎样的一种关系?
对折1次
对折2次
对折3次
对折1次
对折2次
对折3次
1
2
2
4
4
8
1
2
2
4
4
8
=
=
把一个分数化成同它相等,且分子、分母都比原来小的分数的过程,叫约分。
让我们一起学习约分的知识吧。
新知探究
1
彩色卡片占全部卡片的几分之几?
这堆卡片有50张,其中30张是彩色卡片。
彩色卡片占全部卡片的 。
你能把 化成分子、分母都比较小的分数吗?
30
50
用分数的基本性质,把分子和分母同时缩小相同的倍数。
=
15
25
30
50
30÷2
50÷2
=
=
6
10
30
50
30÷5
50÷5
=
=
30
50
30÷10
50÷10
3
5
=
30
50
=
=
15
25
6
10
=
3
5
从中你发现了什么?
它们的分子和分母越来越小。
像这样,把一个分数化成同它相等,且分子分母都比较小的分数的过程,叫做约分。
30
50
还有更简便的方法。
25
15
5
3
3
5
=
分子、分母同时除以公因数2,再除以公因数5。
方法一
30
50
5
3
3
5
=
分子、分母同时除以它们的最大公因数10。
方法二
这两种方法有哪些相同的地方,有哪些不同的地方?
都是把化简成,所以都是约分。
约分的过程不同,方法一约分了两次,方法二是约分了一次。
你能具体地解释一下,这两种不同的约分的过程吗?
方法一是用分子、分母的公因数一次一次地去化简。
方法二是用分子、分母的最大公因数一次化简。
把 , , 化成最简分数。
试 一 试
(教材第30页“试一试”)
18
24
6
18
10
35
18
24
4
3
3
4
=
分子、分母同时除以它们的最大公因数6。
6
18
3
1
1
3
=
(教材第30页“试一试”)
10
35
分子、分母同时除以它们的最大公因数5。
2
7
2
7
=
课堂练习
(教材第30页“课堂活动” )
不是最简分数,它的分子、分母有公因数2,3,6。
一个同学任意写出一个分数,另一个同学判断这个分数是不是最简分数,并说出理由。
6
18
判断一个分数是不是最简分数时,我们应用到了哪些知识呢?
应用到了分数的基本性质、公因数、最大公因数等知识。
2.化简。
12
27
10
25
先找出分子和分母的最大公因数。
最大公因数3
4
9
2
5
=
2
5
4
9
=
最大公因数5
(教材第32页“练习九”第1题)
28
42
24
30
30
45
4
5
最大公因数6
4
5
=
最大公因数15
2
3
2
3
=
最大公因数14
2
3
2
3
=
3.客车的辆数是货车的几分之几?
(教材第32页“练习九”第2题)
停车场有42辆货车,36辆客车,8辆小轿车。
3.客车的辆数是货车的几分之几?
(教材第32页“练习九”第2题)
36
42
6
7
=
答:客车的辆数是货车的 。
6
7
1.货车的辆数是客车的几分之几?
2.小轿车的辆数是客车的几分之几?
3.客车的辆数是小轿车的几分之几?
4.小轿车的辆数是货车的几分之几?
5.货车的辆数是小轿车的几分之几?
你还可以提出哪些数学问题?
1. 2. 3. 4. 5.
7
6
21
4
4
21
9
2
2
9
这节课你有什么收获?
课堂小结
把一个分数化成同它相等,且分子分母都比较小的分数的过程,叫做约分。
分子和分母只有公因数1的分数叫做最简分数。
这节课你有什么收获?
约分的方法
(1)逐次约分法,用分子、分母同时除以它们的公因数,一直到分子、分母只有公因数1为止。
(2)一次约分法,用分子和分母同时除以它们的最大公因数。
02
01
课后作业
课后练习九。
作业课件中的相关练习。
