小学数学西师大版五年级下3.3 长方体、正方体的表面积 课件(共36张PPT)
文档属性
| 名称 | 小学数学西师大版五年级下3.3 长方体、正方体的表面积 课件(共36张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-03 07:38:17 | ||
图片预览



文档简介
(共36张PPT)
西师大版数学五年级(下)
第3课时 长方体、正方体的表面积
长方体 正方体
三
认识长方体和正方体的展开图,理解表面积的意义。
探索长方体和正方体表面积的计算方法,能运用长方体和正方体表面积的知识解决实际问题。
培养空间观念和分析、解决实际问题的能力。
学习目标
【重点】
知道长方体和正方体表面积的计算方法。
【难点】
根据给出的长方体的长、宽、高,想象出每个面的长和宽各是多少,并会求每一个面的面积。
课堂导入
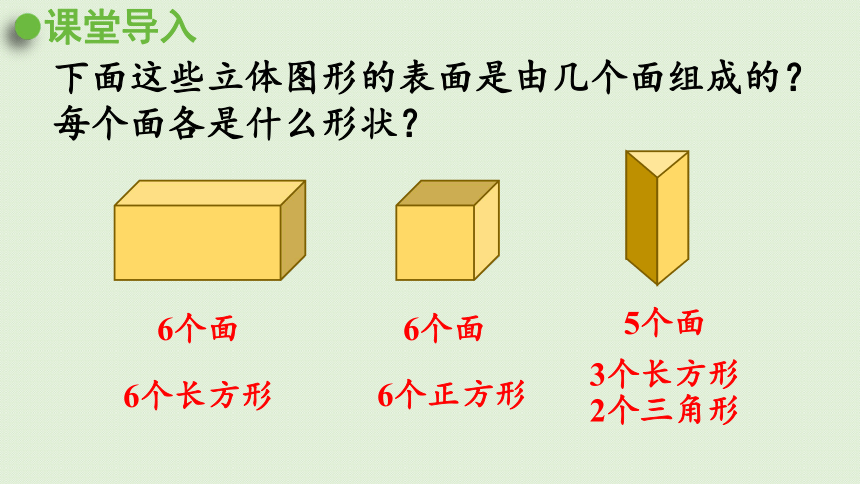
下面这些立体图形的表面是由几个面组成的?每个面各是什么形状?
6个面
6个面
5个面
6个长方形
6个正方形
3个长方形
2个三角形
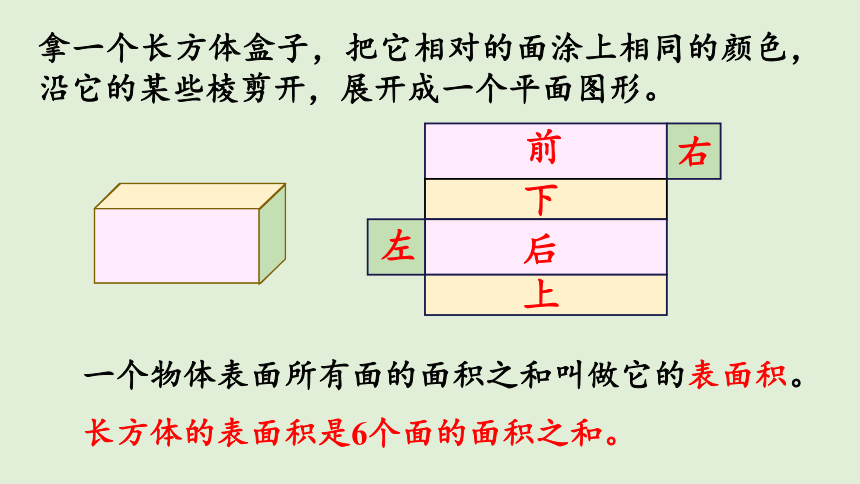
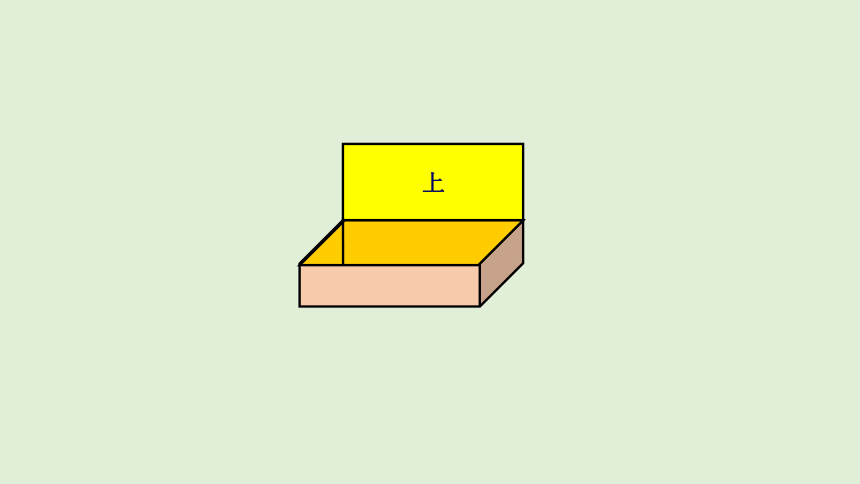
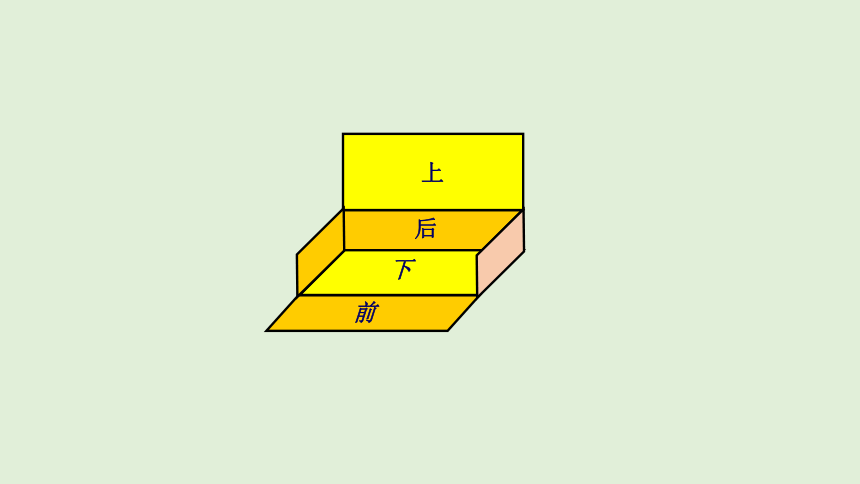
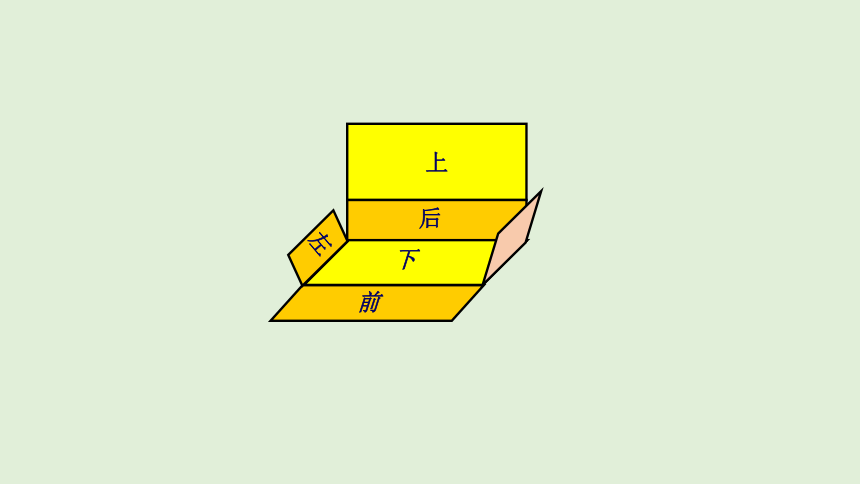
拿一个长方体盒子,把它相对的面涂上相同的颜色,沿它的某些棱剪开,展开成一个平面图形。
前
右
下
后
上
左
一个物体表面所有面的面积之和叫做它的表面积。
长方体的表面积是6个面的面积之和。
上
下
后
前
左
右
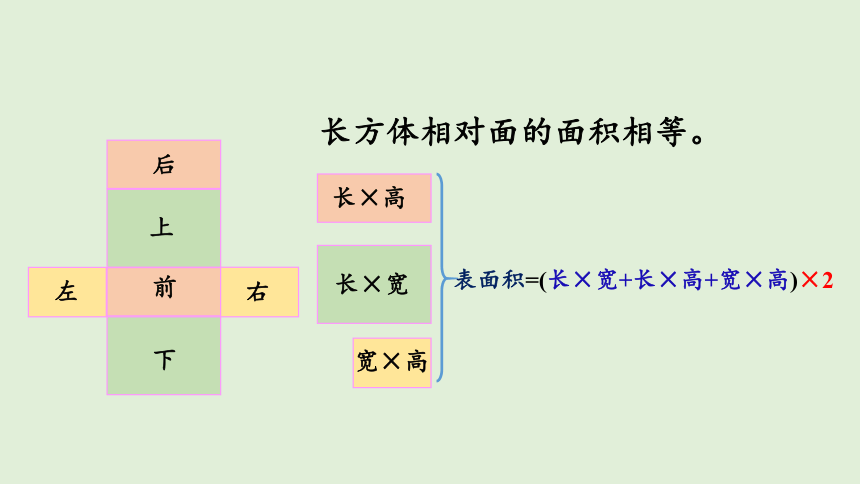
长方体相对面的面积相等。
长×高
长×宽
宽×高
表面积=(长×宽+长×高+宽×高)×2
上
下
后
前
左
右
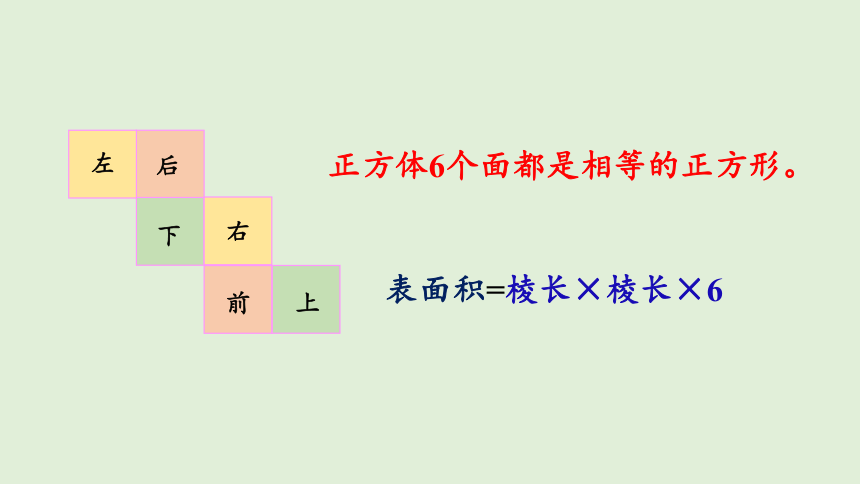
正方体6个面都是相等的正方形。
表面积=棱长×棱长×6
新知探究
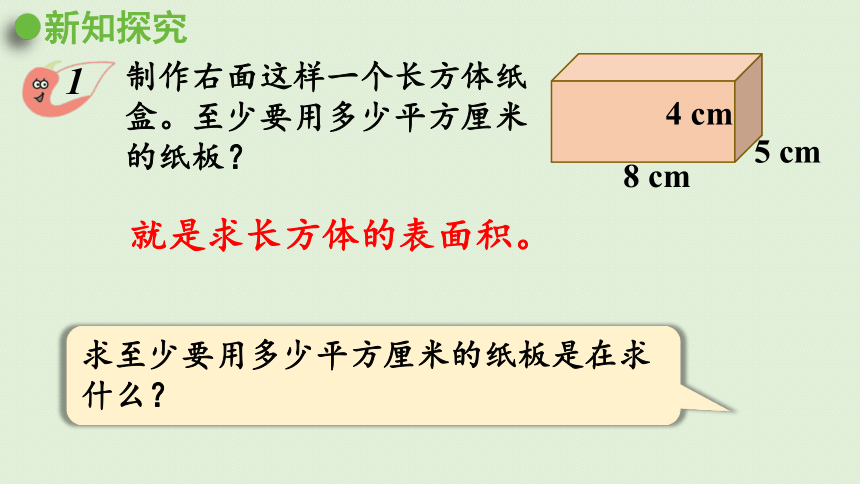
制作右面这样一个长方体纸盒。至少要用多少平方厘米的纸板?
1
求至少要用多少平方厘米的纸板是在求什么?
8 cm
4 cm
5 cm
就是求长方体的表面积。
上
上
下
前
后
上
下
前
后
左
上
下
前
后
左
右
上
下
前
后
左
右
上
下
前
后
左
右
下
前
后
上
左
右
上
下
前
后
左
右
怎样算长方体的表面积呢?
前
右
下
后
上
左
8 cm
5 cm
4 cm
4 cm
5 cm
8 cm
4 cm
5 cm
8 cm
4 cm
5 cm
上
前
右
8 cm
5 cm
60 cm2
总结:长方体上面(或下面)的面积=长×宽
(1)它上、下每个面的长是____ ,宽是 _____,
面积是 。
8 cm
5 cm
上
前
右
8 cm
4 cm
32 cm2
总结:长方体前面(或后面)的面积=长×高
(2)它前、后每个面的长是____ ,宽是 _____,
面积是 。
4 cm
8 cm
5 cm
上
前
右
5 cm
4 cm
20 cm2
总结:长方体左面(或右面)的面积=宽×高
(3)它左、右每个面的长是____ ,宽是 _____,
面积是 。
4 cm
上、下每个面,长______,宽_______,面积是__________;
前、后每个面,长______,宽_______,面积是__________;
左、右每个面,长______,宽_______,面积是__________。
这个纸盒的表面积是:
8 cm
5 cm
40 cm2
8 cm
4 cm
32 cm2
5 cm
4 cm
20 cm2
8×5×2+8×4×2+5×4×2
= (8×5+8×4+5×4)×2
= (40+32+20)×2
= 92×2
= 184(cm2)
答:至少要用184 cm2的纸板。
怎样计算长方体表面积比较简便?
议 一议
长
高
宽
长方体的表面积
=长×宽+长×宽+长×高+长×高+宽×高+宽×高
=(长×宽)×2+(长×高)×2+(宽×高)×2
=(长×宽 + 长×高 + 宽×高)×2
=上面+下面+前面+后面+左面+右面
棱长为2 cm的正方体的表面积是多少?说说理由。
试 一试
2 cm
2 cm
2 cm
正方体的表面积
=上面+下面+前面+后面+左面+右面
=边长×边长
×6
=2×2
×6
=24( cm2 )
答:棱长为2 cm的正方体的表面积是24 cm2 。
10 cm
35 cm
做这样一个纸袋,至少需要多少平方厘米的纸?
2
25 cm
这里需要算几个面的面积?
纸做成纸袋的表面,求至少需要多少平方厘米的纸。
即求纸袋的表面积。
纸袋没有上面。
只需求5个面的面积和。
25×35×2+10×35×2+25×10
= 1750+700+250
= 2500(cm2)
答:至少需要2500 cm2的纸。
做这样一个纸袋,至少需要多少平方厘米的纸?
2
10 cm
35 cm
25 cm
做右图这样一个灯笼(上、下都是空的),至少需要多少绸布?
试 一试
观察灯笼的长宽高,你有什么发现?
长和宽是相等的。
3.5×5×4
= 17.5×4
= 70(dm2)
答:至少需要70 dm2绸布。
在解决与长方体、正方体表面积有关的实际问题时,应当注意些什么?
议一议
在实际生活中,并不是所有长方体形状的物体都有6个面。长方体形状的水桶、鱼缸只有5个面,通风管只有4个面,在计算时应根据实际情况和题中要求做题。
课堂练习
1.一个长方体的大小如图。(图中单位:dm)
(1)上、下两个面的面积和是( )。
(2)前、后两个面的面积和是( )。
(3)左、右两个面的面积和是( )。
(4)表面积是( )。
5
2
2.5
25 dm2
20 dm2
10 dm2
55 dm2
(教材第44页“练习十三”第1题)
2.计算下面长方体和正方体的表面积。(单位:cm)
94 cm2
103 cm2
105.84 cm2
(教材第44页“练习十三”第2题)
一个长方体铁盒,长12 cm,宽10 cm,高8 cm。一个正方体铁盒的棱长是10 cm。这两种铁盒哪种用料少些?
S长方体=
(12×10+12×8+10×8)×2
= 296×2
= 592(cm2)
S正方体=
10×10×6
=100×6
=600(cm2)
592<600
答:长方体铁盒用料少些。
(教材第44页“练习十三”第3题)
某种电冰箱的包装箱形状像一个没有底面的长方体盒子(如图)。做这个包装箱至少要用多少平方分米的纸板?(图中单位:dm)
14×6×2+14×5×2+6×5
= 168+140+30
= 338(dm2)
答:至少需要338 dm2的纸板。
(教材第44页“练习十三”第4题)
课堂小结
这节课你有什么收获?
表面积的意义:一个物体表面所有面的面积之和叫做它的表面积。
长方体或正方体6个面的面积之和就是长方体或正方体的表面积。
这节课你有什么收获?
长方体表面积的计算方式:
长方体的表面积 = 长×宽×2+长×高×2+宽×高×2
= (长×宽 + 长×高 + 宽×高)×2
正方体表面积的计算方式:
正方体的表面积 = 棱长×棱长×6
这节课你有什么收获?
在解决有关长方体和正方体表面积的实际问题时,要注意有的物体可能少1个面、2个面或3个面,要根据实际情况确定计算哪几个面的面积。
这节课你有什么收获?
粉刷教室,不包括屋顶时,共4个面;包括屋顶时,共5个面(都要除去门窗和黑板的面积)。给一个长方体罐头盒贴包装纸,不包括上下面 ,共4个面。方形通风管或烟囱,共4个面。······
02
01
课后作业
课后练习十三。
相关练习。
西师大版数学五年级(下)
第3课时 长方体、正方体的表面积
长方体 正方体
三
认识长方体和正方体的展开图,理解表面积的意义。
探索长方体和正方体表面积的计算方法,能运用长方体和正方体表面积的知识解决实际问题。
培养空间观念和分析、解决实际问题的能力。
学习目标
【重点】
知道长方体和正方体表面积的计算方法。
【难点】
根据给出的长方体的长、宽、高,想象出每个面的长和宽各是多少,并会求每一个面的面积。
课堂导入
下面这些立体图形的表面是由几个面组成的?每个面各是什么形状?
6个面
6个面
5个面
6个长方形
6个正方形
3个长方形
2个三角形
拿一个长方体盒子,把它相对的面涂上相同的颜色,沿它的某些棱剪开,展开成一个平面图形。
前
右
下
后
上
左
一个物体表面所有面的面积之和叫做它的表面积。
长方体的表面积是6个面的面积之和。
上
下
后
前
左
右
长方体相对面的面积相等。
长×高
长×宽
宽×高
表面积=(长×宽+长×高+宽×高)×2
上
下
后
前
左
右
正方体6个面都是相等的正方形。
表面积=棱长×棱长×6
新知探究
制作右面这样一个长方体纸盒。至少要用多少平方厘米的纸板?
1
求至少要用多少平方厘米的纸板是在求什么?
8 cm
4 cm
5 cm
就是求长方体的表面积。
上
上
下
前
后
上
下
前
后
左
上
下
前
后
左
右
上
下
前
后
左
右
上
下
前
后
左
右
下
前
后
上
左
右
上
下
前
后
左
右
怎样算长方体的表面积呢?
前
右
下
后
上
左
8 cm
5 cm
4 cm
4 cm
5 cm
8 cm
4 cm
5 cm
8 cm
4 cm
5 cm
上
前
右
8 cm
5 cm
60 cm2
总结:长方体上面(或下面)的面积=长×宽
(1)它上、下每个面的长是____ ,宽是 _____,
面积是 。
8 cm
5 cm
上
前
右
8 cm
4 cm
32 cm2
总结:长方体前面(或后面)的面积=长×高
(2)它前、后每个面的长是____ ,宽是 _____,
面积是 。
4 cm
8 cm
5 cm
上
前
右
5 cm
4 cm
20 cm2
总结:长方体左面(或右面)的面积=宽×高
(3)它左、右每个面的长是____ ,宽是 _____,
面积是 。
4 cm
上、下每个面,长______,宽_______,面积是__________;
前、后每个面,长______,宽_______,面积是__________;
左、右每个面,长______,宽_______,面积是__________。
这个纸盒的表面积是:
8 cm
5 cm
40 cm2
8 cm
4 cm
32 cm2
5 cm
4 cm
20 cm2
8×5×2+8×4×2+5×4×2
= (8×5+8×4+5×4)×2
= (40+32+20)×2
= 92×2
= 184(cm2)
答:至少要用184 cm2的纸板。
怎样计算长方体表面积比较简便?
议 一议
长
高
宽
长方体的表面积
=长×宽+长×宽+长×高+长×高+宽×高+宽×高
=(长×宽)×2+(长×高)×2+(宽×高)×2
=(长×宽 + 长×高 + 宽×高)×2
=上面+下面+前面+后面+左面+右面
棱长为2 cm的正方体的表面积是多少?说说理由。
试 一试
2 cm
2 cm
2 cm
正方体的表面积
=上面+下面+前面+后面+左面+右面
=边长×边长
×6
=2×2
×6
=24( cm2 )
答:棱长为2 cm的正方体的表面积是24 cm2 。
10 cm
35 cm
做这样一个纸袋,至少需要多少平方厘米的纸?
2
25 cm
这里需要算几个面的面积?
纸做成纸袋的表面,求至少需要多少平方厘米的纸。
即求纸袋的表面积。
纸袋没有上面。
只需求5个面的面积和。
25×35×2+10×35×2+25×10
= 1750+700+250
= 2500(cm2)
答:至少需要2500 cm2的纸。
做这样一个纸袋,至少需要多少平方厘米的纸?
2
10 cm
35 cm
25 cm
做右图这样一个灯笼(上、下都是空的),至少需要多少绸布?
试 一试
观察灯笼的长宽高,你有什么发现?
长和宽是相等的。
3.5×5×4
= 17.5×4
= 70(dm2)
答:至少需要70 dm2绸布。
在解决与长方体、正方体表面积有关的实际问题时,应当注意些什么?
议一议
在实际生活中,并不是所有长方体形状的物体都有6个面。长方体形状的水桶、鱼缸只有5个面,通风管只有4个面,在计算时应根据实际情况和题中要求做题。
课堂练习
1.一个长方体的大小如图。(图中单位:dm)
(1)上、下两个面的面积和是( )。
(2)前、后两个面的面积和是( )。
(3)左、右两个面的面积和是( )。
(4)表面积是( )。
5
2
2.5
25 dm2
20 dm2
10 dm2
55 dm2
(教材第44页“练习十三”第1题)
2.计算下面长方体和正方体的表面积。(单位:cm)
94 cm2
103 cm2
105.84 cm2
(教材第44页“练习十三”第2题)
一个长方体铁盒,长12 cm,宽10 cm,高8 cm。一个正方体铁盒的棱长是10 cm。这两种铁盒哪种用料少些?
S长方体=
(12×10+12×8+10×8)×2
= 296×2
= 592(cm2)
S正方体=
10×10×6
=100×6
=600(cm2)
592<600
答:长方体铁盒用料少些。
(教材第44页“练习十三”第3题)
某种电冰箱的包装箱形状像一个没有底面的长方体盒子(如图)。做这个包装箱至少要用多少平方分米的纸板?(图中单位:dm)
14×6×2+14×5×2+6×5
= 168+140+30
= 338(dm2)
答:至少需要338 dm2的纸板。
(教材第44页“练习十三”第4题)
课堂小结
这节课你有什么收获?
表面积的意义:一个物体表面所有面的面积之和叫做它的表面积。
长方体或正方体6个面的面积之和就是长方体或正方体的表面积。
这节课你有什么收获?
长方体表面积的计算方式:
长方体的表面积 = 长×宽×2+长×高×2+宽×高×2
= (长×宽 + 长×高 + 宽×高)×2
正方体表面积的计算方式:
正方体的表面积 = 棱长×棱长×6
这节课你有什么收获?
在解决有关长方体和正方体表面积的实际问题时,要注意有的物体可能少1个面、2个面或3个面,要根据实际情况确定计算哪几个面的面积。
这节课你有什么收获?
粉刷教室,不包括屋顶时,共4个面;包括屋顶时,共5个面(都要除去门窗和黑板的面积)。给一个长方体罐头盒贴包装纸,不包括上下面 ,共4个面。方形通风管或烟囱,共4个面。······
02
01
课后作业
课后练习十三。
相关练习。
