小学数学西师大版五年级下3.6 长方体和正方体的体积计算 课件(共30张PPT)
文档属性
| 名称 | 小学数学西师大版五年级下3.6 长方体和正方体的体积计算 课件(共30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-03 07:42:13 | ||
图片预览





文档简介
(共30张PPT)
西师大版数学五年级(下)
第6课时 长方体和正方体的体积计算
长方体 正方体
三
经历探索长方体、正方体体积计算方法的过程,总结出长方体和正方体的体积计算公式。
掌握长方体和正方体体积计算公式,能运用公式正确计算长方体和正方体的体积。
在探究体积公式的过程中,培养创新意识和自主探索能力,在数学活动中养成与人合作的良好习惯。
学习目标
【重点】
长方体、正方体的体积计算的推导过程及应用。
【难点】
会运用公式正确计算长方体和正方体
的体积。
1
2
3
4
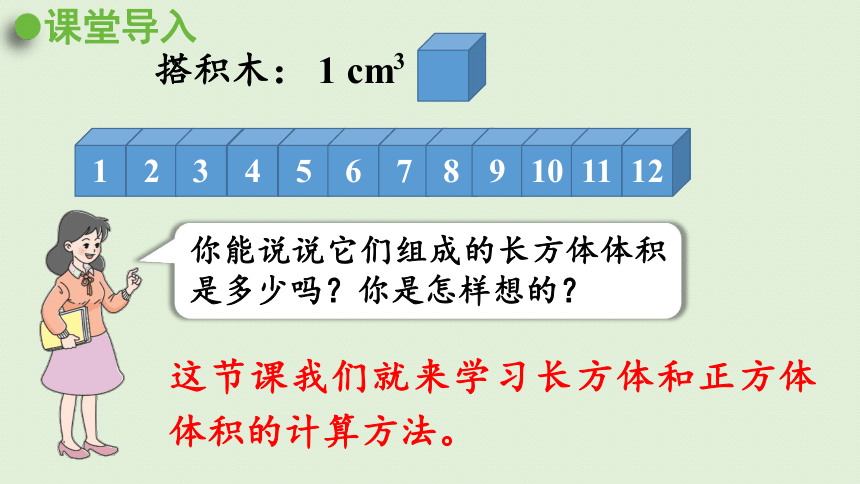
课堂导入
你能说说它们组成的长方体体积是多少吗?你是怎样想的?
这节课我们就来学习长方体和正方体体积的计算方法。
5
6
7
8
9
10
11
12
搭积木: 1 cm
3
新知探究
1
用一些体积为1 cm 的正方体积木拼长方体。
3
要求至少拼出3种不同形状的长方体。
1
2
3
4
5
6
7
8
1 cm
1 cm
8 cm
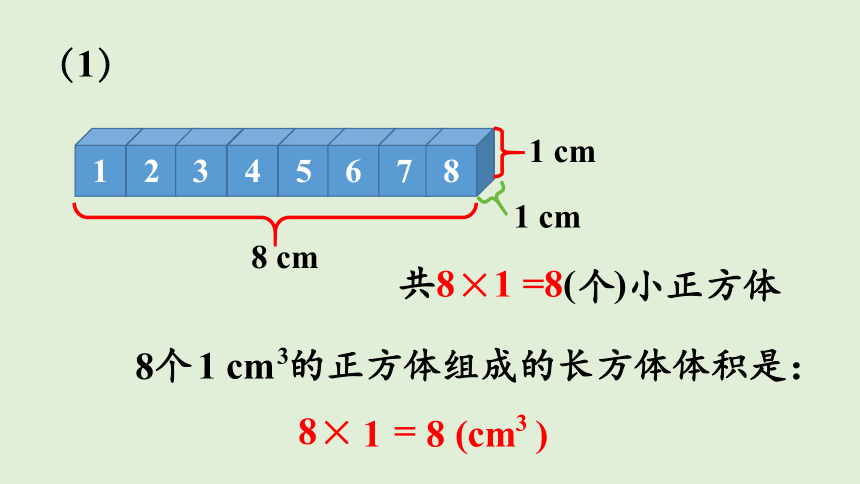
8个 的正方体组成的长方体体积是:
1 cm
3
8× =
1
8 (cm )
3
(1)
共8×1 =8(个)小正方体
1
2
3
4
5
6
7
8
2 cm
1 cm
8 cm
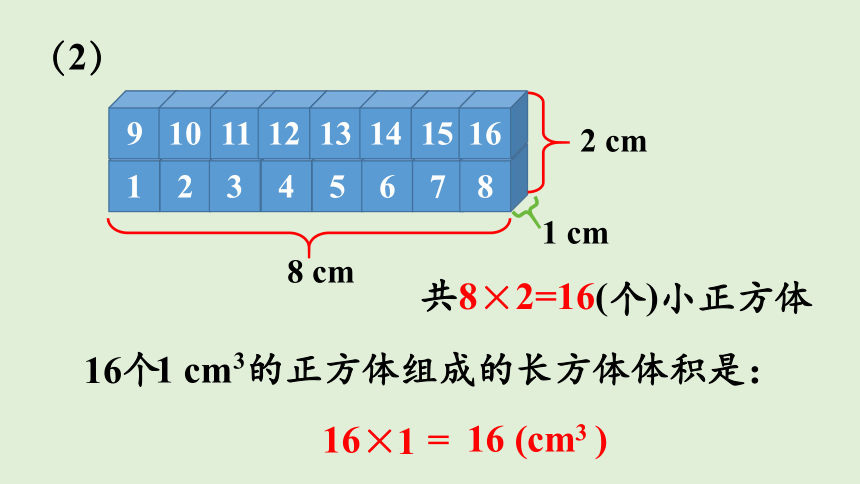
16个 的正方体组成的长方体体积是:
1 cm
3
16× =
1
16 (cm )
3
9
10
11
12
13
14
15
16
(2)
共8×2=16(个)小正方体
2 cm
2 cm
8 cm
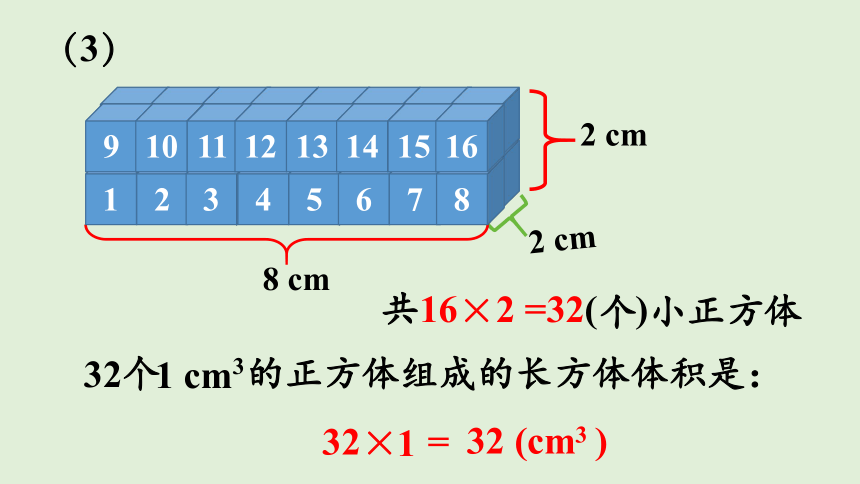
32个 的正方体组成的长方体体积是:
1 cm
3
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(3)
32× =
1
32 (cm )
3
共16×2 =32(个)小正方体
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
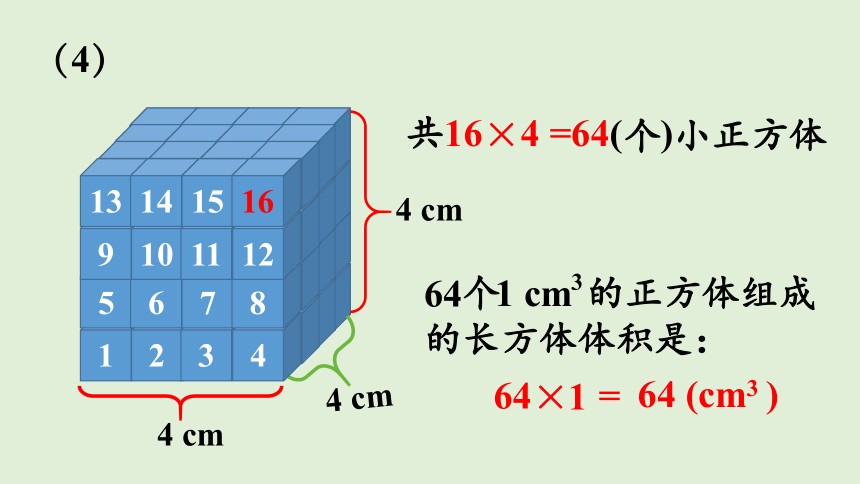
4 cm
4 cm
4 cm
64个 的正方体组成
的长方体体积是:
1 cm
3
(4)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
共16×4 =64(个)小正方体
64× =
1
64 (cm )
3
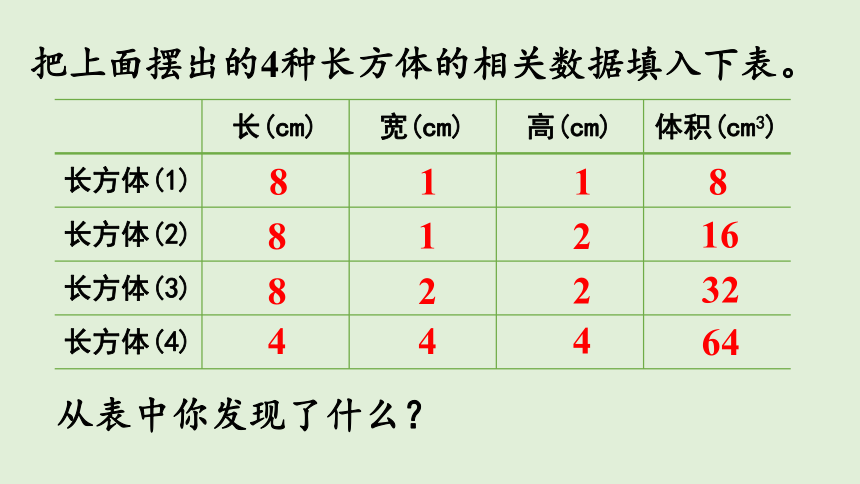
把上面摆出的4种长方体的相关数据填入下表。
长(cm) 宽(cm) 高(cm) 体积(cm3)
长方体(1)
长方体(2)
长方体(3)
长方体(4)
8
1
1
8
8
2
2
32
2
16
8
1
4
4
4
64
从表中你发现了什么?
体积为1 cm3的正方体的个数
层数
行数
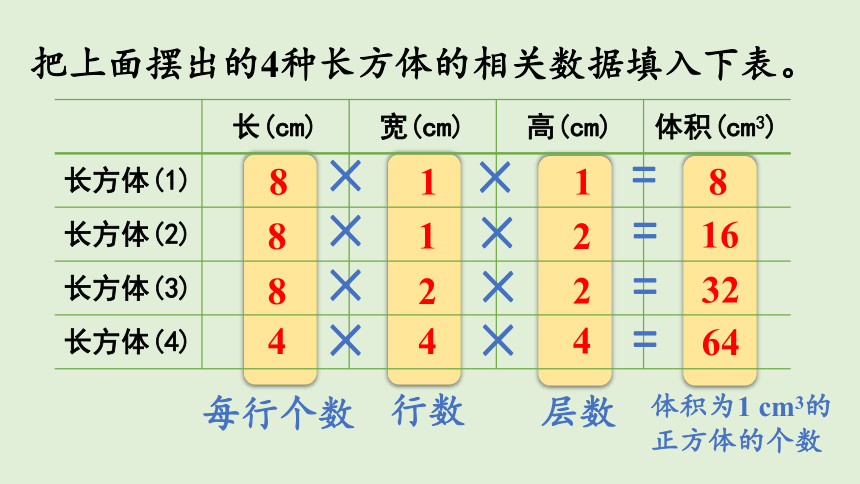
把上面摆出的4种长方体的相关数据填入下表。
长(cm) 宽(cm) 高(cm) 体积(cm3)
长方体(1)
长方体(2)
长方体(3)
长方体(4)
8
1
1
8
8
2
2
32
2
16
8
1
4
4
4
64
每行个数
×
×
=
×
×
=
×
×
=
×
×
=
长方体所含单位体积的个数
=
每行个数
×
行数
×
层数
长方体的体积
=
长
×
宽
×
高
长方体的体积=长×宽×高
比 一 比
长方体的底面积 = 长×宽
正方体的底面积 = 棱长×棱长
长方体或正方体底面的面积叫做底面积。
长
宽
高
底面
棱长
棱长
棱长
底面
长方体的体积 = 长×宽×高
底面积
正方体的体积 = 棱长×棱长×棱长
底面积
= 底面积×高
= 底面积×高
长
宽
高
底面
棱长
棱长
棱长
底面
所以,长方体和正方体的体积也可以这样来计算。
长方体(或正方体)的体积 = 底面积×高
如果用字母 S 表示底面积,上面的公式可以写成:
V = S h
如果用字母 V 表示长方体的体积,用 a,b,h 分别表示长方体的长、宽、高,那么长方体的体积公式可以写成:
V = a b h
a
h
b
如果用字母 V 表示正方体的体积,用 a 表示它
的棱长,那么正方体的体积公式可以写成:
a
a
a
V = a · a · a
a · a · a 也可以写作 “a3”,读作“a 的立方”,表示 3 个 a 相乘。
正方体的体积公式一般写成: V = a3
60×30×20
= 1800×20
= 36000 (cm3)
2
这个水果箱的体积是多少?
我们可以直接用长×宽×高算出体积。
30 cm
60 cm
20 cm
30×60
= 1800 (cm2)
2
这个水果箱的体积是多少?
也可以先算出底面面积,再用底面积×高算出体积。
30 cm
60 cm
20 cm
1800×20
= 36000 (cm3)
课堂练习
(教材第51页“练习十五” 第1题)
1.求体积。
17 cm
4.5 cm
9 cm
9 cm
9 cm
8 cm
17×4.5×8 =
612(cm3)
9×9×9 =
729(cm3)
=6×4×4=96
(cm3)
方法二:
V正方体= a3
= 2×2×2 =8 (cm3)
8×12 = 96
(cm3)
方法一:
V长方体 = a b h
下图是一个由棱长为2 cm的正方体积木组成的长方体,计算它的体积。
(教材第51页“练习十五”)第2题
工人正在为光明小学修建一个游泳池,游泳池的长、宽、高分别为50 m、12 m、1.3 m。
V = a b h
= 50×12×1.3
= 780 (m3)
(教材第51页“练习十五”)第3题
4.一根长方体木料,长5 m,横截面的面积
是0.06 m2。 这根木料的体积是多少?
0.06 m2
长方体体积=底面积×高
0.06×5=0.3(m3)
答:这根木料的体积是0.3m3。
如果用下面的长方体木料截出一个最大的正方体,这个正方体的体积是多少?
(教材第52页“思考题”)
11 cm
6 cm
2 cm
最多可以截多少个这样的正方体?
截出最大正方体的体积为:
V =a3=2×2×2=8(cm3)
(教材第52页“思考题”)
11 cm
6 cm
2 cm
1 cm
(教材第52页“思考题”)
11 cm
6 cm
2 cm
1 cm
10 cm
因为:11÷2=5······1,所以长方体只能取到长10 cm进行计算,最多可以截多少个这样的正方体?
(教材第52页“思考题”)
10×6×2 = 120(cm3)
120÷8 = 15(个)
答:正方体体积是8 cm ,最多可以截15个这样的正方体。
截出最大正方体的体积为:
V =a3=2×2×2=8(cm3)
课堂小结
这节课你有什么收获?
长方体和正方体的体积计算公式
长方体的体积 = 长×宽×高
正方体的体积 = 棱长×棱长×棱长
V = a b h
V = a · a · a = a3
这节课你有什么收获?
长方体和正方体的统一方式:
长(正)方体的体积 = 底面积×高
高 = 体积÷底面积
底面积 = 体积÷高
V = S h
05
03
课后作业
课后练习十五。
相关练习。
西师大版数学五年级(下)
第6课时 长方体和正方体的体积计算
长方体 正方体
三
经历探索长方体、正方体体积计算方法的过程,总结出长方体和正方体的体积计算公式。
掌握长方体和正方体体积计算公式,能运用公式正确计算长方体和正方体的体积。
在探究体积公式的过程中,培养创新意识和自主探索能力,在数学活动中养成与人合作的良好习惯。
学习目标
【重点】
长方体、正方体的体积计算的推导过程及应用。
【难点】
会运用公式正确计算长方体和正方体
的体积。
1
2
3
4
课堂导入
你能说说它们组成的长方体体积是多少吗?你是怎样想的?
这节课我们就来学习长方体和正方体体积的计算方法。
5
6
7
8
9
10
11
12
搭积木: 1 cm
3
新知探究
1
用一些体积为1 cm 的正方体积木拼长方体。
3
要求至少拼出3种不同形状的长方体。
1
2
3
4
5
6
7
8
1 cm
1 cm
8 cm
8个 的正方体组成的长方体体积是:
1 cm
3
8× =
1
8 (cm )
3
(1)
共8×1 =8(个)小正方体
1
2
3
4
5
6
7
8
2 cm
1 cm
8 cm
16个 的正方体组成的长方体体积是:
1 cm
3
16× =
1
16 (cm )
3
9
10
11
12
13
14
15
16
(2)
共8×2=16(个)小正方体
2 cm
2 cm
8 cm
32个 的正方体组成的长方体体积是:
1 cm
3
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(3)
32× =
1
32 (cm )
3
共16×2 =32(个)小正方体
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
4 cm
4 cm
4 cm
64个 的正方体组成
的长方体体积是:
1 cm
3
(4)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
共16×4 =64(个)小正方体
64× =
1
64 (cm )
3
把上面摆出的4种长方体的相关数据填入下表。
长(cm) 宽(cm) 高(cm) 体积(cm3)
长方体(1)
长方体(2)
长方体(3)
长方体(4)
8
1
1
8
8
2
2
32
2
16
8
1
4
4
4
64
从表中你发现了什么?
体积为1 cm3的正方体的个数
层数
行数
把上面摆出的4种长方体的相关数据填入下表。
长(cm) 宽(cm) 高(cm) 体积(cm3)
长方体(1)
长方体(2)
长方体(3)
长方体(4)
8
1
1
8
8
2
2
32
2
16
8
1
4
4
4
64
每行个数
×
×
=
×
×
=
×
×
=
×
×
=
长方体所含单位体积的个数
=
每行个数
×
行数
×
层数
长方体的体积
=
长
×
宽
×
高
长方体的体积=长×宽×高
比 一 比
长方体的底面积 = 长×宽
正方体的底面积 = 棱长×棱长
长方体或正方体底面的面积叫做底面积。
长
宽
高
底面
棱长
棱长
棱长
底面
长方体的体积 = 长×宽×高
底面积
正方体的体积 = 棱长×棱长×棱长
底面积
= 底面积×高
= 底面积×高
长
宽
高
底面
棱长
棱长
棱长
底面
所以,长方体和正方体的体积也可以这样来计算。
长方体(或正方体)的体积 = 底面积×高
如果用字母 S 表示底面积,上面的公式可以写成:
V = S h
如果用字母 V 表示长方体的体积,用 a,b,h 分别表示长方体的长、宽、高,那么长方体的体积公式可以写成:
V = a b h
a
h
b
如果用字母 V 表示正方体的体积,用 a 表示它
的棱长,那么正方体的体积公式可以写成:
a
a
a
V = a · a · a
a · a · a 也可以写作 “a3”,读作“a 的立方”,表示 3 个 a 相乘。
正方体的体积公式一般写成: V = a3
60×30×20
= 1800×20
= 36000 (cm3)
2
这个水果箱的体积是多少?
我们可以直接用长×宽×高算出体积。
30 cm
60 cm
20 cm
30×60
= 1800 (cm2)
2
这个水果箱的体积是多少?
也可以先算出底面面积,再用底面积×高算出体积。
30 cm
60 cm
20 cm
1800×20
= 36000 (cm3)
课堂练习
(教材第51页“练习十五” 第1题)
1.求体积。
17 cm
4.5 cm
9 cm
9 cm
9 cm
8 cm
17×4.5×8 =
612(cm3)
9×9×9 =
729(cm3)
=6×4×4=96
(cm3)
方法二:
V正方体= a3
= 2×2×2 =8 (cm3)
8×12 = 96
(cm3)
方法一:
V长方体 = a b h
下图是一个由棱长为2 cm的正方体积木组成的长方体,计算它的体积。
(教材第51页“练习十五”)第2题
工人正在为光明小学修建一个游泳池,游泳池的长、宽、高分别为50 m、12 m、1.3 m。
V = a b h
= 50×12×1.3
= 780 (m3)
(教材第51页“练习十五”)第3题
4.一根长方体木料,长5 m,横截面的面积
是0.06 m2。 这根木料的体积是多少?
0.06 m2
长方体体积=底面积×高
0.06×5=0.3(m3)
答:这根木料的体积是0.3m3。
如果用下面的长方体木料截出一个最大的正方体,这个正方体的体积是多少?
(教材第52页“思考题”)
11 cm
6 cm
2 cm
最多可以截多少个这样的正方体?
截出最大正方体的体积为:
V =a3=2×2×2=8(cm3)
(教材第52页“思考题”)
11 cm
6 cm
2 cm
1 cm
(教材第52页“思考题”)
11 cm
6 cm
2 cm
1 cm
10 cm
因为:11÷2=5······1,所以长方体只能取到长10 cm进行计算,最多可以截多少个这样的正方体?
(教材第52页“思考题”)
10×6×2 = 120(cm3)
120÷8 = 15(个)
答:正方体体积是8 cm ,最多可以截15个这样的正方体。
截出最大正方体的体积为:
V =a3=2×2×2=8(cm3)
课堂小结
这节课你有什么收获?
长方体和正方体的体积计算公式
长方体的体积 = 长×宽×高
正方体的体积 = 棱长×棱长×棱长
V = a b h
V = a · a · a = a3
这节课你有什么收获?
长方体和正方体的统一方式:
长(正)方体的体积 = 底面积×高
高 = 体积÷底面积
底面积 = 体积÷高
V = S h
05
03
课后作业
课后练习十五。
相关练习。
