小学数学西师大版五年级下3.10 设计长方体的包装方案 课件(共16张PPT)
文档属性
| 名称 | 小学数学西师大版五年级下3.10 设计长方体的包装方案 课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-03 00:00:00 | ||
图片预览





文档简介
(共16张PPT)
西师大版数学五年级(下)
第10课时 设计长方体的包装方案
长方体、正方体
三
学习目标
通过设计长方体的包装方案让学生认识到在体积相同的情况下,表面积与它的长、宽、高的相差程度有关的道理。
通过数学活动,运用所学知识,获得解决简单实际问题的经验、方法以及成功的体验。
通过动手操作和实践,培养学数学、用数学、爱数学的积极数学情感。
【重点】
理解在体积相等的情况下,要使表面积较小,长、宽、高应越接近的道理。
【难点】
动手操作摆放,形成不同的长方体。寻找
最节省的包装方案。
情境导入
同学们准备买些文具盒送给新村小学的学生,需要把文具盒包装一下。设计怎样的包装方案更节省包装纸?
我们买些文具盒送给新村小学的学生。
把文具盒包装一下。
新知探究
1.想一想,包装物品可能要
涉及哪些问题?
形状
包装纸的大小
动手摆一摆吧!
将你摆成的长方体的长、宽、高记录下来,算一算按你的包装方案进行包装至少需要用多少包装纸。(接口处不计。)
长
宽
高
长
宽
高
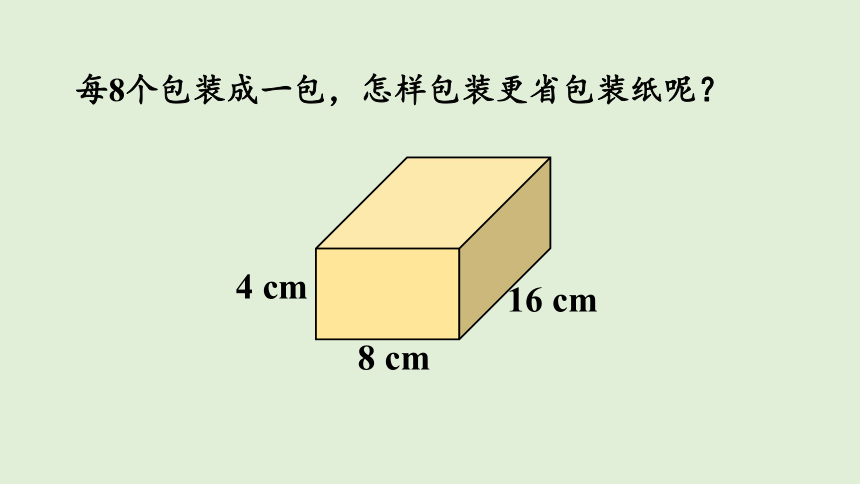
每8个包装成一包,怎样包装更省包装纸呢?
16 cm
8 cm
4 cm
方案一
表面积:
(16×8×8+8×4×8+16×4)×2 =
2688(cm2)
表面积:
(16×8×2×4+8×4×4+16×4×2)×2=
2560(cm2)
方案二
表面积:
(8×4×8+16×4×8+8×16)×2 =
1792(cm2)
方案三
表面积:
(8×4×2×4+16×4×4+16×8×2)×2 =
1536(cm2)
方案四
比较不同的包装方案,你有什么发现?
2688(cm2)
1792(cm2)
2560(cm2)
1563(cm2)
物体重合的面积越大,表面积就越小,包装用的纸也就越少。
同样的体积下,长方体的表面积与它的长、宽、高的长度有关,长、宽、高的长度越接近,表面积就越小,当长、宽、高相等时,它的表面积最小。
比较不同的包装方案,你有什么发现?
包装的问题生活中很常见,除了节省之外,我们还需要考虑哪些因素呢
1、大小适当。
2、单个包装物的重量合适,越大越重,包装纸
要能承受得住。
3、方便运输。
4、防水,防跌落。
这节课你有什么收获?
活动总结
在包装中,想要更节省包装纸,就是要把物体最大的那个面更多地重叠起来;同时要根据物体的长、宽、高以及数量的多少,通过实际测量计算所需的包装纸。当摆成的长方体的长、宽、高越接近时,包装所需要的包装纸越少。
活动拓展
请你了解一下,生活中有哪些涉及省料的问题?并与同学交流。
1、装修;
2、木工做家具;
3、盖房子;
······
西师大版数学五年级(下)
第10课时 设计长方体的包装方案
长方体、正方体
三
学习目标
通过设计长方体的包装方案让学生认识到在体积相同的情况下,表面积与它的长、宽、高的相差程度有关的道理。
通过数学活动,运用所学知识,获得解决简单实际问题的经验、方法以及成功的体验。
通过动手操作和实践,培养学数学、用数学、爱数学的积极数学情感。
【重点】
理解在体积相等的情况下,要使表面积较小,长、宽、高应越接近的道理。
【难点】
动手操作摆放,形成不同的长方体。寻找
最节省的包装方案。
情境导入
同学们准备买些文具盒送给新村小学的学生,需要把文具盒包装一下。设计怎样的包装方案更节省包装纸?
我们买些文具盒送给新村小学的学生。
把文具盒包装一下。
新知探究
1.想一想,包装物品可能要
涉及哪些问题?
形状
包装纸的大小
动手摆一摆吧!
将你摆成的长方体的长、宽、高记录下来,算一算按你的包装方案进行包装至少需要用多少包装纸。(接口处不计。)
长
宽
高
长
宽
高
每8个包装成一包,怎样包装更省包装纸呢?
16 cm
8 cm
4 cm
方案一
表面积:
(16×8×8+8×4×8+16×4)×2 =
2688(cm2)
表面积:
(16×8×2×4+8×4×4+16×4×2)×2=
2560(cm2)
方案二
表面积:
(8×4×8+16×4×8+8×16)×2 =
1792(cm2)
方案三
表面积:
(8×4×2×4+16×4×4+16×8×2)×2 =
1536(cm2)
方案四
比较不同的包装方案,你有什么发现?
2688(cm2)
1792(cm2)
2560(cm2)
1563(cm2)
物体重合的面积越大,表面积就越小,包装用的纸也就越少。
同样的体积下,长方体的表面积与它的长、宽、高的长度有关,长、宽、高的长度越接近,表面积就越小,当长、宽、高相等时,它的表面积最小。
比较不同的包装方案,你有什么发现?
包装的问题生活中很常见,除了节省之外,我们还需要考虑哪些因素呢
1、大小适当。
2、单个包装物的重量合适,越大越重,包装纸
要能承受得住。
3、方便运输。
4、防水,防跌落。
这节课你有什么收获?
活动总结
在包装中,想要更节省包装纸,就是要把物体最大的那个面更多地重叠起来;同时要根据物体的长、宽、高以及数量的多少,通过实际测量计算所需的包装纸。当摆成的长方体的长、宽、高越接近时,包装所需要的包装纸越少。
活动拓展
请你了解一下,生活中有哪些涉及省料的问题?并与同学交流。
1、装修;
2、木工做家具;
3、盖房子;
······
