小学数学西师大版五年级下5.7 第五单元 方程 问题解决(二)课件(共22张PPT)
文档属性
| 名称 | 小学数学西师大版五年级下5.7 第五单元 方程 问题解决(二)课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-03 00:00:00 | ||
图片预览








文档简介
(共22张PPT)
西师大版数学五年级(下)
第7课时 问题解决(二)
方程
五
能根据等量关系构建方程,并解决较复杂的实际问题。体验方程思想在解决数量关系稍复杂的(含两个未知数的和倍、差倍等)实际问题中的作用。
在丰富感性认识的基础上探索新知,理解新知,应用新知,
在解决问题的过程中,体会方程解决问题的优点,增强学习数学的兴趣。
学习目标
【重点】
根据等量关系构建方程,解决较复杂的以及涉及两个未知条件的现实问题。
【难点】
能根据情境,找出稍复杂的(含两个未
知数的和倍、差倍等)问题中的等量关系。
课堂导入
列方程解决问题的一般步骤:
1.根据题意找出等量关系式。
2.找出未知数,并用x表示。
3.根据等量关系式列出方程、解方程。
4.检验,并写出答语。
说一说用方程解决问题的步骤。
新知探究
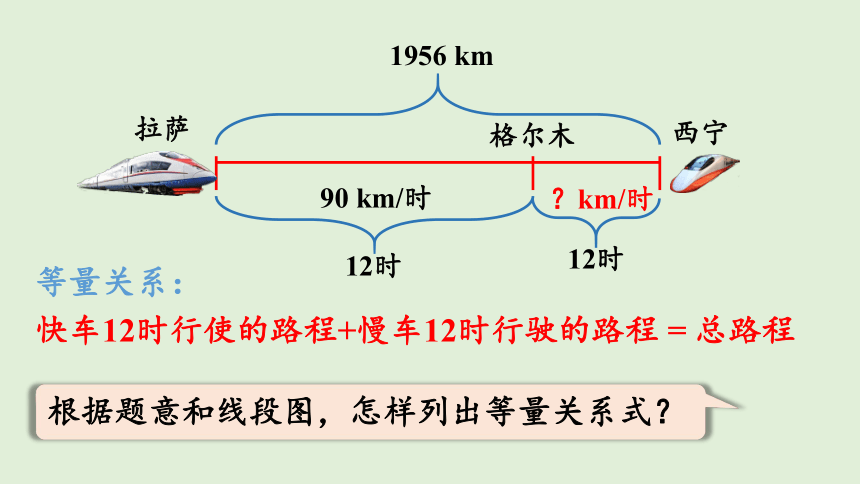
青藏铁路是世界最长的高原铁路,东起青海西宁,西至西藏拉萨,全长1956 km。两列火车分别从拉萨和西宁同时出发,经过12时在格尔木相遇。已知快车平均每时行驶90 km,慢车平均每时行驶多少千米?
3
1956 km
拉萨
西宁
格尔木
12时
90 km/时
12时
?km/时
等量关系:
快车12时行使的路程+慢车12时行驶的路程 = 总路程
根据题意和线段图,怎样列出等量关系式?
解:设慢车平均每时行驶 x千米。
90×12+12 x = 1956
1080+12 x = 1956
答:慢车平均每时行驶73千米。
12 x = 876
x = 73
等量关系:
快车12时行使的路程+慢车12时行驶的路程 = 总路程
你还能列出哪些方程?
试 一 试
(快车的速度+慢车的速度)×12 = 总路程
总路程-快车12时行使的路程 = 慢车12时行驶的路程
(90+x)×12 = 1956
1956-12×90 = 12x
小刚和小明去买一种奥运会纪念邮票。小刚买了8 张,小明买了5 张,小明比小刚少用了6元。每张邮票多少元?
4
说一说题中的已知条件和问题。
已知:
问题:
小刚买8张,小明买5张,小明比小刚少用6元。
每张邮票多少元?
等量关系:
小刚用的钱-小明用的钱 = 6
解:设每张邮票x元。
8 x -5 x = 6
3 x = 6
答:每张邮票2元。
x = 2
等量关系:
小刚用的钱-小明用的钱 = 6
花卉园里种了牡丹和郁金香,牡丹的株数是郁金香的3倍。
(1) 牡丹和郁金香一共有240株,牡丹和郁金香各有
多少株?
(2) 牡丹比郁金香多120株,牡丹和郁金香各有多少
株?
这里有两个未知数,怎样设呢?
(1)
解:设牡丹有x株。
则郁金香有240-x株
或郁金香有x÷3株。
(2)
解:设牡丹有x株。
则郁金香有x-120株
或郁金香有x÷3株。
(1)
解:设牡丹有x株。
(240- x)×3 = x
x+x÷3 = 240
720-3x = x
4x = 720
x = 180
3x+x = 720
4x = 720
x = 180
花卉园里种了牡丹和郁金香,牡丹的株数是郁金香的3倍。
(1) 牡丹和郁金香一共有240株,牡丹和郁金香各有
多少株?
(2) 牡丹比郁金香多120株,牡丹和郁金香各有多少
株?
或
180÷3 = 60
牡丹:180(株)
郁金香:60(株)
花卉园里种了牡丹和郁金香,牡丹的株数是郁金香的3倍。
(1) 牡丹和郁金香一共有240株,牡丹和郁金香各有
多少株?
(2) 牡丹比郁金香多120株,牡丹和郁金香各有多少
株?
(2)
解:设牡丹有x株。
(x-120)×3 = x
x- x÷3 = 120
3x-360 = x
2x = 360
x = 180
3x- x = 360
2x = 360
x = 180
或
180÷3 = 60
牡丹:180(株)
郁金香:60(株)
课堂练习
2007年国家向西部地区投资19.2亿元,用于重点县的“退牧还草”工程。如果平均分成4个季度投资,每个县平均1个季度投资0.05 亿元,一共有多少个重点县获得投资?
重点县个数×4×每季投资额=总投资
解:设一共有x个重点县获得投资。
4×0.05x = 19.2
0.2x = 19.2
x = 96
答:一共有96个重点县获得投资。
(教材第90页“练习二十五”第6题)
一辆客车和一辆轿车同时从贵阳开往重庆,客车每时行75 km。经过2时后,轿车比客车多开了50 km。轿车每时行多少千米?
轿车路程-客车路程 = 50 km
解:设轿车每时行x千米。
2x-75×2 = 50
2x = 200
x = 100
答:轿车每时行100千米。
(教材第90页“练习二十五”第7题)
3.小明买了5本练习本,小华买了同样的9本。
解:每本练习本的单价是x元。
9x - 5x = 14
4 x = 14
x = 3.5
答:小明付17.5元,小华付31.5元。
3.5×5 =
3.5×9 =
17.5(元)
31.5(元)
(教材第90页“练习二十五”第8题)
小华付的钱数-小明付的钱数 = 14
(教材第90页“练习二十五”第9题)
4.甲船每时行20 km,乙船每时行28 km。
解:设x时后两船相遇。
20x + 28x = 504
48x = 504
x = 10.5
下午1时经过10.5时后是晚上11:30。
答:两船在晚上11点30分会相遇。
下午1时,两船分别从洛阳和新镇相对开出,在什么时候会相遇呢?
(教材第90页“思考题”)
欣欣木器加工厂有70名技术工人。每个工人平均每天能加工10张课桌或者15张方凳。为了供应市场,必须1张课桌与2张方凳配成一套发货。怎样安排加工课桌和方凳的人数,才能既不造成浪费,又能满足供货?
1张课桌与2张方凳配成一套
课桌的张数×2 = 方凳的张数
每人每天加工课桌张数×加工课桌的人数× 2
= 每人每天加工方凳张数×加工方凳的人数
(教材第90页“思考题”)
每人每天加工课桌张数×加工课桌的人数× 2
= 每人每天加工方凳张数×加工方凳的人数
解:设有x名工人加工课桌,则有(70 - x)名工人加工方凳。
10×x×2 = 15×(70-x)
20x = 15×70-15x
20x = 1050-15x
答:安排30名工人加工课桌,40名工人加工方凳。
20x+15x = 1050
35x = 1050
x = 30
70-30 = 40(名)
这节课你有什么收获?
课堂小结
用方程解和倍(差倍)问题时,先设其中一个未知量为x(通常设一倍量为x),再根据两个未知量之间的关系,用含有x的式子表示另一个未知量,然后根据这两个量的和(差),列出形如ax±bx=c的方程,最后进行解答。
这节课你有什么收获?
形如ax±bx = c的方程的解法:
ax+bx = c
解:(a+b)x = c
(a+b)x÷(a+b) = c÷(a+b)
x = c÷(a+b)
ax+bx = c
解:(a+b)x = c
(a+b)x÷(a+b) = c÷(a+b)
x = c÷(a+b)
02
01
课后作业
课后练习二十五。
相关练习。
西师大版数学五年级(下)
第7课时 问题解决(二)
方程
五
能根据等量关系构建方程,并解决较复杂的实际问题。体验方程思想在解决数量关系稍复杂的(含两个未知数的和倍、差倍等)实际问题中的作用。
在丰富感性认识的基础上探索新知,理解新知,应用新知,
在解决问题的过程中,体会方程解决问题的优点,增强学习数学的兴趣。
学习目标
【重点】
根据等量关系构建方程,解决较复杂的以及涉及两个未知条件的现实问题。
【难点】
能根据情境,找出稍复杂的(含两个未
知数的和倍、差倍等)问题中的等量关系。
课堂导入
列方程解决问题的一般步骤:
1.根据题意找出等量关系式。
2.找出未知数,并用x表示。
3.根据等量关系式列出方程、解方程。
4.检验,并写出答语。
说一说用方程解决问题的步骤。
新知探究
青藏铁路是世界最长的高原铁路,东起青海西宁,西至西藏拉萨,全长1956 km。两列火车分别从拉萨和西宁同时出发,经过12时在格尔木相遇。已知快车平均每时行驶90 km,慢车平均每时行驶多少千米?
3
1956 km
拉萨
西宁
格尔木
12时
90 km/时
12时
?km/时
等量关系:
快车12时行使的路程+慢车12时行驶的路程 = 总路程
根据题意和线段图,怎样列出等量关系式?
解:设慢车平均每时行驶 x千米。
90×12+12 x = 1956
1080+12 x = 1956
答:慢车平均每时行驶73千米。
12 x = 876
x = 73
等量关系:
快车12时行使的路程+慢车12时行驶的路程 = 总路程
你还能列出哪些方程?
试 一 试
(快车的速度+慢车的速度)×12 = 总路程
总路程-快车12时行使的路程 = 慢车12时行驶的路程
(90+x)×12 = 1956
1956-12×90 = 12x
小刚和小明去买一种奥运会纪念邮票。小刚买了8 张,小明买了5 张,小明比小刚少用了6元。每张邮票多少元?
4
说一说题中的已知条件和问题。
已知:
问题:
小刚买8张,小明买5张,小明比小刚少用6元。
每张邮票多少元?
等量关系:
小刚用的钱-小明用的钱 = 6
解:设每张邮票x元。
8 x -5 x = 6
3 x = 6
答:每张邮票2元。
x = 2
等量关系:
小刚用的钱-小明用的钱 = 6
花卉园里种了牡丹和郁金香,牡丹的株数是郁金香的3倍。
(1) 牡丹和郁金香一共有240株,牡丹和郁金香各有
多少株?
(2) 牡丹比郁金香多120株,牡丹和郁金香各有多少
株?
这里有两个未知数,怎样设呢?
(1)
解:设牡丹有x株。
则郁金香有240-x株
或郁金香有x÷3株。
(2)
解:设牡丹有x株。
则郁金香有x-120株
或郁金香有x÷3株。
(1)
解:设牡丹有x株。
(240- x)×3 = x
x+x÷3 = 240
720-3x = x
4x = 720
x = 180
3x+x = 720
4x = 720
x = 180
花卉园里种了牡丹和郁金香,牡丹的株数是郁金香的3倍。
(1) 牡丹和郁金香一共有240株,牡丹和郁金香各有
多少株?
(2) 牡丹比郁金香多120株,牡丹和郁金香各有多少
株?
或
180÷3 = 60
牡丹:180(株)
郁金香:60(株)
花卉园里种了牡丹和郁金香,牡丹的株数是郁金香的3倍。
(1) 牡丹和郁金香一共有240株,牡丹和郁金香各有
多少株?
(2) 牡丹比郁金香多120株,牡丹和郁金香各有多少
株?
(2)
解:设牡丹有x株。
(x-120)×3 = x
x- x÷3 = 120
3x-360 = x
2x = 360
x = 180
3x- x = 360
2x = 360
x = 180
或
180÷3 = 60
牡丹:180(株)
郁金香:60(株)
课堂练习
2007年国家向西部地区投资19.2亿元,用于重点县的“退牧还草”工程。如果平均分成4个季度投资,每个县平均1个季度投资0.05 亿元,一共有多少个重点县获得投资?
重点县个数×4×每季投资额=总投资
解:设一共有x个重点县获得投资。
4×0.05x = 19.2
0.2x = 19.2
x = 96
答:一共有96个重点县获得投资。
(教材第90页“练习二十五”第6题)
一辆客车和一辆轿车同时从贵阳开往重庆,客车每时行75 km。经过2时后,轿车比客车多开了50 km。轿车每时行多少千米?
轿车路程-客车路程 = 50 km
解:设轿车每时行x千米。
2x-75×2 = 50
2x = 200
x = 100
答:轿车每时行100千米。
(教材第90页“练习二十五”第7题)
3.小明买了5本练习本,小华买了同样的9本。
解:每本练习本的单价是x元。
9x - 5x = 14
4 x = 14
x = 3.5
答:小明付17.5元,小华付31.5元。
3.5×5 =
3.5×9 =
17.5(元)
31.5(元)
(教材第90页“练习二十五”第8题)
小华付的钱数-小明付的钱数 = 14
(教材第90页“练习二十五”第9题)
4.甲船每时行20 km,乙船每时行28 km。
解:设x时后两船相遇。
20x + 28x = 504
48x = 504
x = 10.5
下午1时经过10.5时后是晚上11:30。
答:两船在晚上11点30分会相遇。
下午1时,两船分别从洛阳和新镇相对开出,在什么时候会相遇呢?
(教材第90页“思考题”)
欣欣木器加工厂有70名技术工人。每个工人平均每天能加工10张课桌或者15张方凳。为了供应市场,必须1张课桌与2张方凳配成一套发货。怎样安排加工课桌和方凳的人数,才能既不造成浪费,又能满足供货?
1张课桌与2张方凳配成一套
课桌的张数×2 = 方凳的张数
每人每天加工课桌张数×加工课桌的人数× 2
= 每人每天加工方凳张数×加工方凳的人数
(教材第90页“思考题”)
每人每天加工课桌张数×加工课桌的人数× 2
= 每人每天加工方凳张数×加工方凳的人数
解:设有x名工人加工课桌,则有(70 - x)名工人加工方凳。
10×x×2 = 15×(70-x)
20x = 15×70-15x
20x = 1050-15x
答:安排30名工人加工课桌,40名工人加工方凳。
20x+15x = 1050
35x = 1050
x = 30
70-30 = 40(名)
这节课你有什么收获?
课堂小结
用方程解和倍(差倍)问题时,先设其中一个未知量为x(通常设一倍量为x),再根据两个未知量之间的关系,用含有x的式子表示另一个未知量,然后根据这两个量的和(差),列出形如ax±bx=c的方程,最后进行解答。
这节课你有什么收获?
形如ax±bx = c的方程的解法:
ax+bx = c
解:(a+b)x = c
(a+b)x÷(a+b) = c÷(a+b)
x = c÷(a+b)
ax+bx = c
解:(a+b)x = c
(a+b)x÷(a+b) = c÷(a+b)
x = c÷(a+b)
02
01
课后作业
课后练习二十五。
相关练习。
