西师大版 五年级下册数学 5.8 第五单元 方程 整理与复习 课件(共34张PPT)
文档属性
| 名称 | 西师大版 五年级下册数学 5.8 第五单元 方程 整理与复习 课件(共34张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-03 12:11:24 | ||
图片预览








文档简介
(共34张PPT)
西师大版数学五年级(下)
第8课时 整理与复习
方程
五
学习目标
回顾用字母表示数和数量关系、等式和方程的意义,加强对这部分知识的理解。讨论方程与等式的关系,进一步掌握方程与等式的区别和联系。
交流写方程和解方程的基本方法,会按正确的步骤解方程,能熟练地运用方程解决问题。
通过复习的过程中,自主学习,培养独立思考的能力。通过小组合作,培养合作的意识和能力。
【重点】
全面回顾方程的相关知识和能用方程解决问题。
【难点】
能从实际情境中找出等量关系并写出方程。
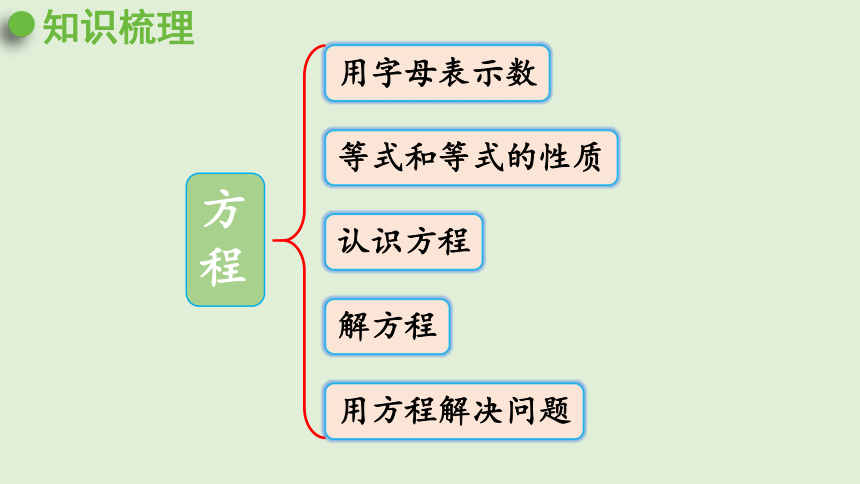
知识梳理
方程
用字母表示数
解方程
认识方程
等式和等式的性质
用方程解决问题
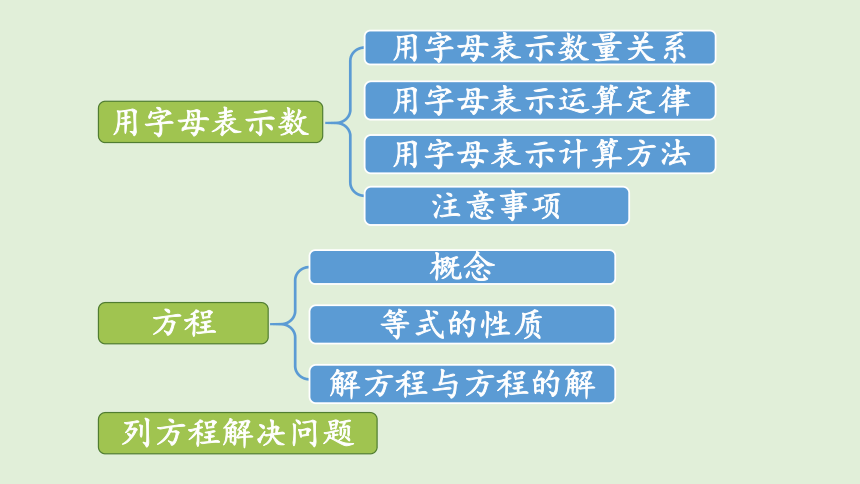
用字母表示数
概念
等式的性质
方程
用字母表示数量关系
用字母表示运算定律
用字母表示计算方法
注意事项
解方程与方程的解
列方程解决问题
要点回顾
用字母可以表示数,在含有字母的式子中,数字和字母、字母和字母之间的称号可以记作“·”,可省略不写;数字通常写在字母的前面。
用字母可以表示一个数、数量关系和公式运算律、计算公式等使记忆变得简单。
用字母表示数
用字母表示数
注意事项
用字母表示数量关系
路程=速度×时间
s=vt
总价=单价×数量
c=an
工作总量=工作效率×工作时间
c=at
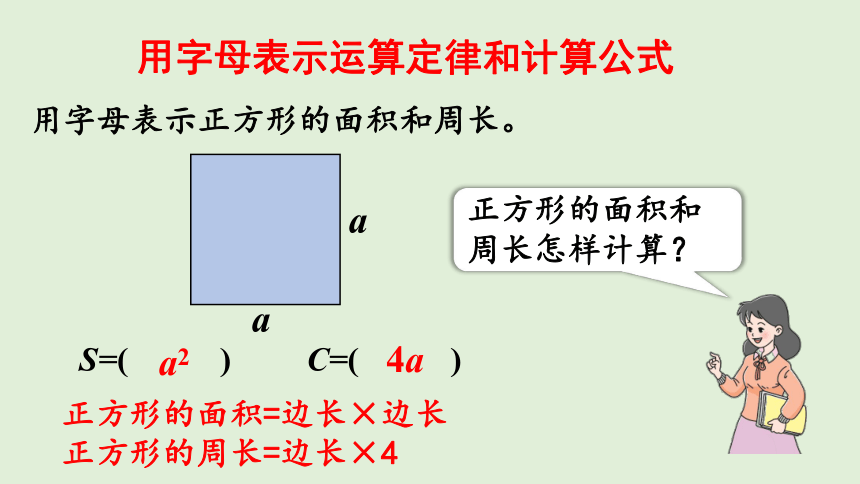
用字母表示正方形的面积和周长。
S=( ) C=( )
a
a
a2
4a
正方形的面积和周长怎样计算?
正方形的面积=边长×边长
正方形的周长=边长×4
用字母表示运算定律和计算公式
名称 用字母表示
加法交换律
加法结合律
乘法交换律
乘法结合律
乘法分配律
a+b=b+a
(a+b)+c=a+(b+c)
a×b=b×a
(a×b)×c=a×(b×c)
(a+b)×c=a×c+b×c
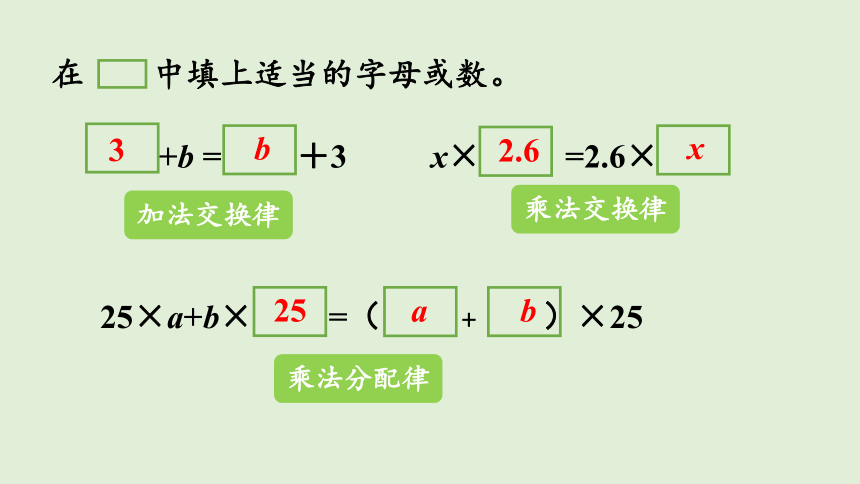
用字母表示运算律
3
b
x
2.6
25
b
a
加法交换律
乘法交换律
乘法分配律
在 中填上适当的字母或数。
+b = +3 x× =2.6×
25×a+b× =( + )×25
等式的两边同时加或减一个相同的数,得到的结果仍然是等式;
等式的两边同时乘或除以一个相同的数(0不作除数),得到的结果仍然是等式。
2a = b
2a×2-6 = b×2-6
等式及等式的性质
含有未知数的等式叫做方程。
1.判断一个式子是否是方程的两个必要条件:
(1)含有未知数。
(2)必须是等式。
2.根据数学信息写等式时,先找出题中的等量关系,
然后根据等量关系写出方程或等式。
认识方程
求出方程解的过程叫做解方程。
使方程左右两边相等的未知数的值,叫做方程的解。
根据等式的基本性质求方程的解。
检验方程的解是否正确时,把方程的解代入到方程,通过计算看方程的左右两边是否相等。
解方程
用方程解决问题的步骤
(教材第56页“练习二十六”第1题)
课堂练习
1.连线。
a+a
3×12
m3
2a
a+b
m·m·m
4q
b+a
62
q+3q
(教材第56页“练习二十六”第2题)
(1)扎西家养山羊a头,是养牦牛头数的3倍。他家
养牦牛( )头。
(2)一堆煤p吨,一辆汽车10次可以运完。这辆车
平均每次运( )吨。
(3)一个正方体的棱长是a m,它的表面积是
( )m2,体积是( )m3。
3a
p÷10
6a2
a3
2.填空。
(教材第56页“练习二十六”第3题)
3.填出各式表示的值。
a 2 45
5a
34+7a
3a-2.5
a2
10
225
48
349
3.5
132.5
4
2025
(教材第56页“练习二十六”第4题)
4.写出方程,说出数量关系。
1.2+x=2.5
去年收的质量+今年收的质量=一共收的质量
0.8x = 400
每株用的肥料×株数=共用的肥料
(30÷5)x = 240
每畦需要种子量×畦数=需要种子总量
(教材第56页“练习二十六”第5题)
5.解方程。
4x+56=76 6x-18=36
4x+56-56=76-56
解:
4x=20
4x÷4=20÷4
x=5
6x-18+18=36+18
解:
6x=54
6x÷6=54÷6
x=9
(教材第56页“练习二十六”第5题)
5.解方程。
8x-5x = 12
3x = 12
解:
3x÷3 = 12÷3
x = 4
(教材第56页“练习二十六”第6题)
(1)一辆大货车的载货量是10吨,比一辆小货车载货量的8倍少2吨。这辆小货车的载货量是多少吨?
等量关系式:小货车的载货量×8-2=大货车的载货量
解:小货车的载货量x吨。
8x-2=10
8x=12
答:小货车的载货量是1.5吨。
x=1.5
(教材第56页“练习二十六”第6题)
(2) 有100 m布,做了同种规格的儿童服装50套
后,还剩22 m。儿童服装每套用布多少米?
等量关系式:每套儿童服装用布×50+22 = 100
解:儿童服装每套用布x米。
50x+22=100
50x=78
x=1.56
答:儿童服装每套用布1.56米。
(教材第56页“练习二十六”第7题)
7.列方程解下列问题。
(1) 客、货两列火车从相距465 km的两站同时出发,
相对而行, 3时后相遇。这时货车一共行了240 km,
客车每时行多少千米?
等量关系式:货车行的路程+客车行的路程=总路程
解:设客车每时行x千米。
240+3x=465
3x=225
答:客车每时行75千米。
x=75
(教材第56页“练习二十六”第7题)
7.列方程解下列问题。
这个篱笆总长440 米,宽多少米呢?
等量关系式:(长+宽)×2=周长
解:宽是x米。
(180+x)×2=440
360+2x=440
答:宽是40米。
2x=80
x=40
(2)
(教材第56页“练习二十六”第7题)
7.列方程解下列问题。
(3) 你知道3种玩具的单价吗?
等量关系:直升机的单价=摩托车的单价×4
轮船的单价=摩托车的单价+60
直升机的单价是摩托车的4倍 轮船比摩托车贵60元
1架直升机与1辆摩托车 的总价是350元 1艘轮船与1辆摩托车
的总价是200元
(教材第56页“练习二十六”第7题)
解:设摩托车的单价是x元。
4 x + x = 350
5 x = 350
x = 70
直升机的单价:70×4=280(元)
轮船的单价:70+60=130(元)
答:直升机的单价是280元,轮船的单价是130元,摩托车的单价是70元。
方法一
(教材第56页“练习二十六”第7题)
答:直升机的单价是280元,轮船的单价是130元,摩托车的单价是70元。
方法二
解:设摩托车的单价是x元。
x +60+ x = 200
2 x +60 = 200
2 x = 140
x = 70
直升机的单价:70×4=280(元)
轮船的单价:70+60=130(元)
玲玲和军军沿着运动场跑步。
(1)如果两人同时同地开始向相反方向跑,那么经过多
少时间两人第1次相遇?
(2)如果两人同时同地开始向同一方向跑,那么经过多
少时间军军第1次追上玲玲?
(教材第93页“思考题”)
我每秒跑5米。
我每秒跑3米。
军军跑的路程+玲玲跑的路程=跑道周长
我每秒跑3米。
我每秒跑5米。
(教材第93页“思考题”)
(1)如果两人同时同地开始向相反方向跑,那么经过多
少时间两人第1次相遇?
军军跑的路程+玲玲跑的路程=跑道周长
(教材第93页“思考题”)
(1)如果两人同时同地开始向相反方向跑,那么经过多
少时间两人第1次相遇?
解:设经过x秒两人第1次相遇。
5 x +3 x = 400
8 x = 400
x = 50
答:经过50秒两人第1次相遇。
军军跑的路程-玲玲跑的路程=跑道周长
我每秒跑3米。
我每秒跑5米。
(教材第93页“思考题”)
(2)如果两人同时同地开始向同一方向跑,那么经过多
少时间军军第1次追上玲玲?
军军跑的路程-玲玲跑的路程=跑道周长
解:设经过x秒军军第1次追上玲玲。
5 x -3 x = 400
2 x = 400
答:经过200秒军军第1次追上玲玲。
x = 200
(教材第93页“思考题”)
(2)如果两人同时同地开始向同一方向跑,那么经过多
少时间军军第1次追上玲玲?
相关练习。
02
01
课后练习二十六。
课后作业
西师大版数学五年级(下)
第8课时 整理与复习
方程
五
学习目标
回顾用字母表示数和数量关系、等式和方程的意义,加强对这部分知识的理解。讨论方程与等式的关系,进一步掌握方程与等式的区别和联系。
交流写方程和解方程的基本方法,会按正确的步骤解方程,能熟练地运用方程解决问题。
通过复习的过程中,自主学习,培养独立思考的能力。通过小组合作,培养合作的意识和能力。
【重点】
全面回顾方程的相关知识和能用方程解决问题。
【难点】
能从实际情境中找出等量关系并写出方程。
知识梳理
方程
用字母表示数
解方程
认识方程
等式和等式的性质
用方程解决问题
用字母表示数
概念
等式的性质
方程
用字母表示数量关系
用字母表示运算定律
用字母表示计算方法
注意事项
解方程与方程的解
列方程解决问题
要点回顾
用字母可以表示数,在含有字母的式子中,数字和字母、字母和字母之间的称号可以记作“·”,可省略不写;数字通常写在字母的前面。
用字母可以表示一个数、数量关系和公式运算律、计算公式等使记忆变得简单。
用字母表示数
用字母表示数
注意事项
用字母表示数量关系
路程=速度×时间
s=vt
总价=单价×数量
c=an
工作总量=工作效率×工作时间
c=at
用字母表示正方形的面积和周长。
S=( ) C=( )
a
a
a2
4a
正方形的面积和周长怎样计算?
正方形的面积=边长×边长
正方形的周长=边长×4
用字母表示运算定律和计算公式
名称 用字母表示
加法交换律
加法结合律
乘法交换律
乘法结合律
乘法分配律
a+b=b+a
(a+b)+c=a+(b+c)
a×b=b×a
(a×b)×c=a×(b×c)
(a+b)×c=a×c+b×c
用字母表示运算律
3
b
x
2.6
25
b
a
加法交换律
乘法交换律
乘法分配律
在 中填上适当的字母或数。
+b = +3 x× =2.6×
25×a+b× =( + )×25
等式的两边同时加或减一个相同的数,得到的结果仍然是等式;
等式的两边同时乘或除以一个相同的数(0不作除数),得到的结果仍然是等式。
2a = b
2a×2-6 = b×2-6
等式及等式的性质
含有未知数的等式叫做方程。
1.判断一个式子是否是方程的两个必要条件:
(1)含有未知数。
(2)必须是等式。
2.根据数学信息写等式时,先找出题中的等量关系,
然后根据等量关系写出方程或等式。
认识方程
求出方程解的过程叫做解方程。
使方程左右两边相等的未知数的值,叫做方程的解。
根据等式的基本性质求方程的解。
检验方程的解是否正确时,把方程的解代入到方程,通过计算看方程的左右两边是否相等。
解方程
用方程解决问题的步骤
(教材第56页“练习二十六”第1题)
课堂练习
1.连线。
a+a
3×12
m3
2a
a+b
m·m·m
4q
b+a
62
q+3q
(教材第56页“练习二十六”第2题)
(1)扎西家养山羊a头,是养牦牛头数的3倍。他家
养牦牛( )头。
(2)一堆煤p吨,一辆汽车10次可以运完。这辆车
平均每次运( )吨。
(3)一个正方体的棱长是a m,它的表面积是
( )m2,体积是( )m3。
3a
p÷10
6a2
a3
2.填空。
(教材第56页“练习二十六”第3题)
3.填出各式表示的值。
a 2 45
5a
34+7a
3a-2.5
a2
10
225
48
349
3.5
132.5
4
2025
(教材第56页“练习二十六”第4题)
4.写出方程,说出数量关系。
1.2+x=2.5
去年收的质量+今年收的质量=一共收的质量
0.8x = 400
每株用的肥料×株数=共用的肥料
(30÷5)x = 240
每畦需要种子量×畦数=需要种子总量
(教材第56页“练习二十六”第5题)
5.解方程。
4x+56=76 6x-18=36
4x+56-56=76-56
解:
4x=20
4x÷4=20÷4
x=5
6x-18+18=36+18
解:
6x=54
6x÷6=54÷6
x=9
(教材第56页“练习二十六”第5题)
5.解方程。
8x-5x = 12
3x = 12
解:
3x÷3 = 12÷3
x = 4
(教材第56页“练习二十六”第6题)
(1)一辆大货车的载货量是10吨,比一辆小货车载货量的8倍少2吨。这辆小货车的载货量是多少吨?
等量关系式:小货车的载货量×8-2=大货车的载货量
解:小货车的载货量x吨。
8x-2=10
8x=12
答:小货车的载货量是1.5吨。
x=1.5
(教材第56页“练习二十六”第6题)
(2) 有100 m布,做了同种规格的儿童服装50套
后,还剩22 m。儿童服装每套用布多少米?
等量关系式:每套儿童服装用布×50+22 = 100
解:儿童服装每套用布x米。
50x+22=100
50x=78
x=1.56
答:儿童服装每套用布1.56米。
(教材第56页“练习二十六”第7题)
7.列方程解下列问题。
(1) 客、货两列火车从相距465 km的两站同时出发,
相对而行, 3时后相遇。这时货车一共行了240 km,
客车每时行多少千米?
等量关系式:货车行的路程+客车行的路程=总路程
解:设客车每时行x千米。
240+3x=465
3x=225
答:客车每时行75千米。
x=75
(教材第56页“练习二十六”第7题)
7.列方程解下列问题。
这个篱笆总长440 米,宽多少米呢?
等量关系式:(长+宽)×2=周长
解:宽是x米。
(180+x)×2=440
360+2x=440
答:宽是40米。
2x=80
x=40
(2)
(教材第56页“练习二十六”第7题)
7.列方程解下列问题。
(3) 你知道3种玩具的单价吗?
等量关系:直升机的单价=摩托车的单价×4
轮船的单价=摩托车的单价+60
直升机的单价是摩托车的4倍 轮船比摩托车贵60元
1架直升机与1辆摩托车 的总价是350元 1艘轮船与1辆摩托车
的总价是200元
(教材第56页“练习二十六”第7题)
解:设摩托车的单价是x元。
4 x + x = 350
5 x = 350
x = 70
直升机的单价:70×4=280(元)
轮船的单价:70+60=130(元)
答:直升机的单价是280元,轮船的单价是130元,摩托车的单价是70元。
方法一
(教材第56页“练习二十六”第7题)
答:直升机的单价是280元,轮船的单价是130元,摩托车的单价是70元。
方法二
解:设摩托车的单价是x元。
x +60+ x = 200
2 x +60 = 200
2 x = 140
x = 70
直升机的单价:70×4=280(元)
轮船的单价:70+60=130(元)
玲玲和军军沿着运动场跑步。
(1)如果两人同时同地开始向相反方向跑,那么经过多
少时间两人第1次相遇?
(2)如果两人同时同地开始向同一方向跑,那么经过多
少时间军军第1次追上玲玲?
(教材第93页“思考题”)
我每秒跑5米。
我每秒跑3米。
军军跑的路程+玲玲跑的路程=跑道周长
我每秒跑3米。
我每秒跑5米。
(教材第93页“思考题”)
(1)如果两人同时同地开始向相反方向跑,那么经过多
少时间两人第1次相遇?
军军跑的路程+玲玲跑的路程=跑道周长
(教材第93页“思考题”)
(1)如果两人同时同地开始向相反方向跑,那么经过多
少时间两人第1次相遇?
解:设经过x秒两人第1次相遇。
5 x +3 x = 400
8 x = 400
x = 50
答:经过50秒两人第1次相遇。
军军跑的路程-玲玲跑的路程=跑道周长
我每秒跑3米。
我每秒跑5米。
(教材第93页“思考题”)
(2)如果两人同时同地开始向同一方向跑,那么经过多
少时间军军第1次追上玲玲?
军军跑的路程-玲玲跑的路程=跑道周长
解:设经过x秒军军第1次追上玲玲。
5 x -3 x = 400
2 x = 400
答:经过200秒军军第1次追上玲玲。
x = 200
(教材第93页“思考题”)
(2)如果两人同时同地开始向同一方向跑,那么经过多
少时间军军第1次追上玲玲?
相关练习。
02
01
课后练习二十六。
课后作业
