人教版八年级数学上册11.2.1三角形的内角同步课件(共24张PPT)
文档属性
| 名称 | 人教版八年级数学上册11.2.1三角形的内角同步课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-03 00:00:00 | ||
图片预览





文档简介
(共24张PPT)
11.2.1三角形的内角
人教版 初中数学
新课导入
新知探究
练习
应用提高
1
3
4
2
ADD THE TITEL
ADD THE TITEL
ADD THE TITEL
ADD THE TITEL
新课导入
生活中我们常常能看见这样的照片,他们中都有我们熟悉的图形——三角形。学习今天的内容,大家对三角形会有新的认识,下面让我们进入到今天的学习之旅吧!
新知探究
三角形内角和的性质
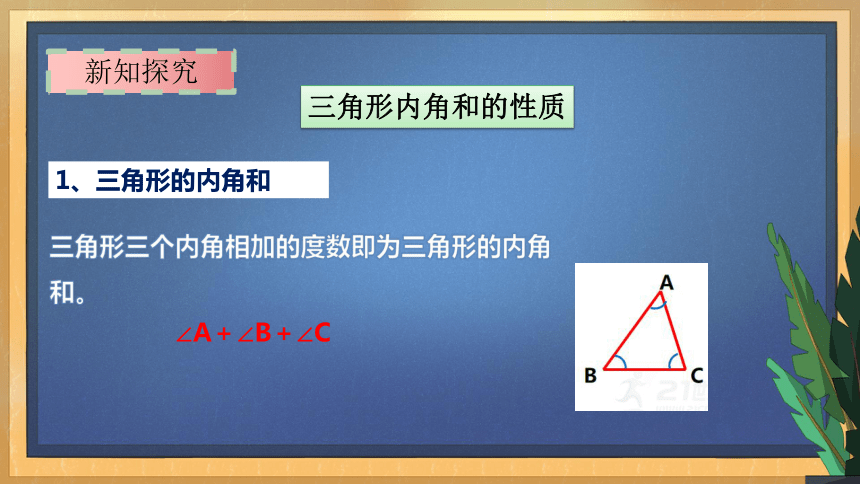
1、三角形的内角和
三角形三个内角相加的度数即为三角形的内角和。
∠A+∠B+∠C
新知探究
想一想
三角形的三个内角和是多少
180°
方法一: 度量法
通过具体的度量,验证三角形的内角和为180°.
绿色圃中小学教育http://www.LSPJY.com 绿色圃中学资源网http://cz.Lspjy.com
绿色圃中小学教育http://www.LSPJY.com 绿色圃中学资源网http://cz.Lspjy.com
新知探究
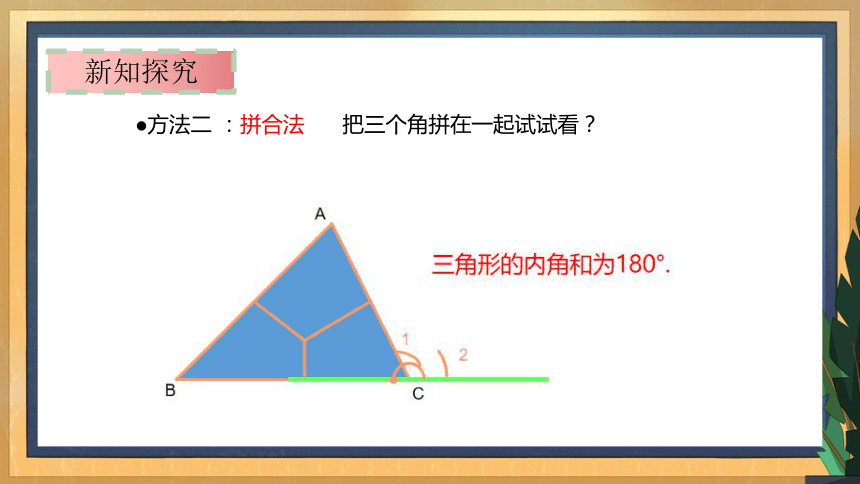
方法二 :拼合法 把三个角拼在一起试试看?
新知探究
问题:有什么方法可以得到180 °
1.平角的度数是180°
2.两直线平行,同旁内角的和是180°
3、邻补角的和是180 °
从刚才拼角的过程你能想出证明的方法吗
新知探究
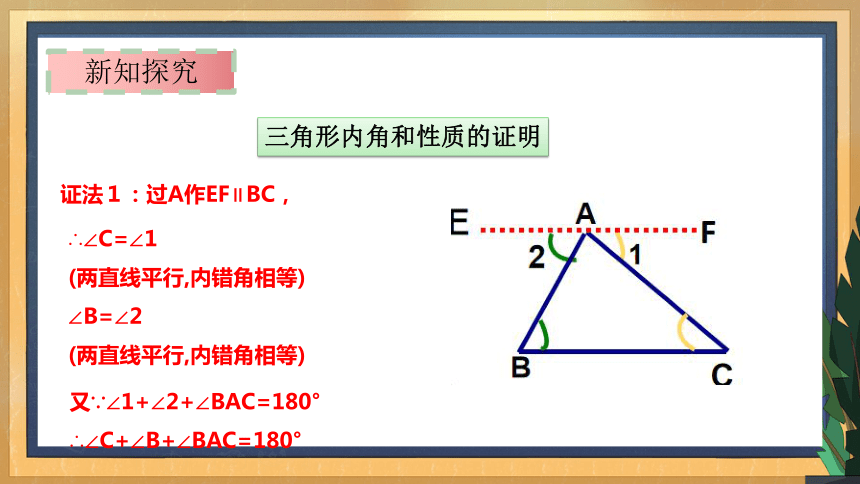
三角形内角和性质的证明
证法1:过A作EF∥BC,
∴∠C=∠1
(两直线平行,内错角相等)
∠B=∠2
(两直线平行,内错角相等)
又∵∠1+∠2+∠BAC=180°
∴∠C+∠B+∠BAC=180°
新知探究
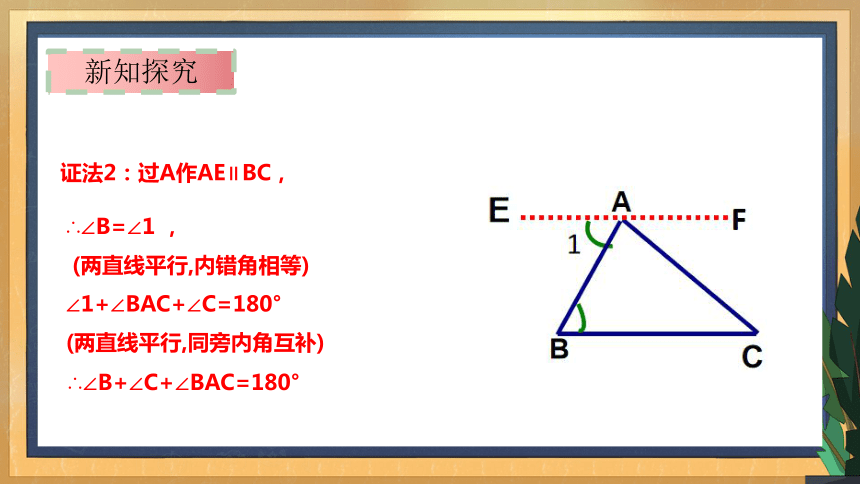
证法2:过A作AE∥BC,
∴∠B=∠1 ,
(两直线平行,内错角相等)
∠1+∠BAC+∠C=180°
(两直线平行,同旁内角互补)
∴∠B+∠C+∠BAC=180°
新知探究
证明3:延长BC到D,过C作CE∥BA,
∴ ∠A=∠1 (两直线平行,内错角相等)
∠B=∠2(两直线平行,同位角相等)
又∵∠1+∠2+∠ACB=180°
∴∠A+∠B+∠ACB=180°
新知探究
在这里,为了证明的需要,在原来的图形上添加的线叫做辅助线。
为了证明三个角的和为180°,转化为一个平角或同旁内角,这种转化思想是数学中的常用方法。
在平面几何里,辅助线通常画成虚线。
∠BAC=40 °
(已知)
∴∠1= ∠BAC=20°
(角平分线定义)
在△ ABD中
∵ ∠1+ ∠B+ ∠ADB=180°
(三角形内角和定理)
∴ ∠ADB=180°-∠1-∠B
=180°-75°-20°
=85°
例1 如图,在△ABC中,∠BAC=40 ° ,∠B=75 ° ,AD是△ ABC的角平分线,求∠ADB的度数。
∵AD是△ ABC的角平分线,
新知探究
新知探究
直角三角形内角和
你能找出上图中所包含的直角三角形吗 ?
新知探究
在Rt△ABC中.
∵∠A+∠B +∠C = 180°,(三角形内角和定理)
而∠C = 90°,
∴ ∠A+∠B = 90°.
直角三角形的两锐角互余.
新知探究
三角形ABC 表示为:
直角三角形可以用符号:
如图直角三角形ABC表示为:
三角形用什么符号表示的?那么直
角三角形又用什么符号表示呢?
△ABC
Rt△
Rt△ABC
新知探究
想一想:如果一个三角形是直角三角形,那么这个三角形有两个角互余.反过来,有两个角互余的三角形是直角三角形吗?请说明理由.
已知:(如图)在△ABC中,
∠A+∠B = 90°.
求证:△ABC是直角三角形.
新知探究
证明:在△ABC中,
∠A+∠B+∠C = 180°,(三角形内角和定理)
∵ ∠A+∠B = 90°,(已知)
∴ ∠C = 90°,
∴ △ABC是直角三角形.(直角三角形定义)
结论:有两个角互余的三角形是直角三角形.
练习
1.下列各组角能构成同一个三角形的三个内角的是( )
A. 34°,36°,50° B.63°,70°,67°
C. 95°,80°,5° D.25°,160°,15°
2.在△ABC中,∠A=60°,∠B=70°,则△ABC是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.无法确定
3.在△ABC中,∠A+∠B=100°,∠C=2∠B,求∠A,∠B,∠C的度数.
解:在△ABC中,
∠C=180°-(∠A+∠B)=80°,
∠B= ∠C=40°,
∠A=100°-∠B=60°
练习
应用提高
1. 如图,在△ABC 中, ∠BAC =40°, ∠B =
75°,AD 是△ABC 的角平分线.求∠ADB 的度数.
解:∵AD平分∠CAB,∠BAC=40°,
∴∠DAB= ∠BAC=20°,
在△ABD 中,
∵∠B=75°,
∴∠ADB=180°-∠B-∠BAD
=180°-20°-75°=85°.
C
B
D
A
应用提高
2. 如图,C 岛在A 岛的北偏东50°方向,B 岛
在A 岛的北偏东80°方向,C 岛在B 岛的北偏西40°方
向.从B 岛看A,C 两岛的视角∠ABC 是多少度?从C
岛看A,B 两岛的视角∠ACB 呢?
解:∠CAB=∠BAD ∠CAD
=80° 50°=30°,
∵AD∥BE,
∴∠BAD+∠ABE=180°,
应用提高
∴∠ABE=180°-∠BAD
=180° 80°=100°
∠ABC=∠ABE-∠EBC
=100° 40°=60°
在△ABC 中,
∠ACB=180° ∠ABC ∠CAB
=180° 60° 30°=90°
答:从B岛看A,C两岛的视角∠ABC是60°,从C岛看A,B两岛的视角∠ACB是90°.
体验收获
今天我们学习了哪些知识?
1.说一说三角形内角和定理?
2.怎样证明三角形内角和定理?
下课休息
11.2.1三角形的内角
人教版 初中数学
新课导入
新知探究
练习
应用提高
1
3
4
2
ADD THE TITEL
ADD THE TITEL
ADD THE TITEL
ADD THE TITEL
新课导入
生活中我们常常能看见这样的照片,他们中都有我们熟悉的图形——三角形。学习今天的内容,大家对三角形会有新的认识,下面让我们进入到今天的学习之旅吧!
新知探究
三角形内角和的性质
1、三角形的内角和
三角形三个内角相加的度数即为三角形的内角和。
∠A+∠B+∠C
新知探究
想一想
三角形的三个内角和是多少
180°
方法一: 度量法
通过具体的度量,验证三角形的内角和为180°.
绿色圃中小学教育http://www.LSPJY.com 绿色圃中学资源网http://cz.Lspjy.com
绿色圃中小学教育http://www.LSPJY.com 绿色圃中学资源网http://cz.Lspjy.com
新知探究
方法二 :拼合法 把三个角拼在一起试试看?
新知探究
问题:有什么方法可以得到180 °
1.平角的度数是180°
2.两直线平行,同旁内角的和是180°
3、邻补角的和是180 °
从刚才拼角的过程你能想出证明的方法吗
新知探究
三角形内角和性质的证明
证法1:过A作EF∥BC,
∴∠C=∠1
(两直线平行,内错角相等)
∠B=∠2
(两直线平行,内错角相等)
又∵∠1+∠2+∠BAC=180°
∴∠C+∠B+∠BAC=180°
新知探究
证法2:过A作AE∥BC,
∴∠B=∠1 ,
(两直线平行,内错角相等)
∠1+∠BAC+∠C=180°
(两直线平行,同旁内角互补)
∴∠B+∠C+∠BAC=180°
新知探究
证明3:延长BC到D,过C作CE∥BA,
∴ ∠A=∠1 (两直线平行,内错角相等)
∠B=∠2(两直线平行,同位角相等)
又∵∠1+∠2+∠ACB=180°
∴∠A+∠B+∠ACB=180°
新知探究
在这里,为了证明的需要,在原来的图形上添加的线叫做辅助线。
为了证明三个角的和为180°,转化为一个平角或同旁内角,这种转化思想是数学中的常用方法。
在平面几何里,辅助线通常画成虚线。
∠BAC=40 °
(已知)
∴∠1= ∠BAC=20°
(角平分线定义)
在△ ABD中
∵ ∠1+ ∠B+ ∠ADB=180°
(三角形内角和定理)
∴ ∠ADB=180°-∠1-∠B
=180°-75°-20°
=85°
例1 如图,在△ABC中,∠BAC=40 ° ,∠B=75 ° ,AD是△ ABC的角平分线,求∠ADB的度数。
∵AD是△ ABC的角平分线,
新知探究
新知探究
直角三角形内角和
你能找出上图中所包含的直角三角形吗 ?
新知探究
在Rt△ABC中.
∵∠A+∠B +∠C = 180°,(三角形内角和定理)
而∠C = 90°,
∴ ∠A+∠B = 90°.
直角三角形的两锐角互余.
新知探究
三角形ABC 表示为:
直角三角形可以用符号:
如图直角三角形ABC表示为:
三角形用什么符号表示的?那么直
角三角形又用什么符号表示呢?
△ABC
Rt△
Rt△ABC
新知探究
想一想:如果一个三角形是直角三角形,那么这个三角形有两个角互余.反过来,有两个角互余的三角形是直角三角形吗?请说明理由.
已知:(如图)在△ABC中,
∠A+∠B = 90°.
求证:△ABC是直角三角形.
新知探究
证明:在△ABC中,
∠A+∠B+∠C = 180°,(三角形内角和定理)
∵ ∠A+∠B = 90°,(已知)
∴ ∠C = 90°,
∴ △ABC是直角三角形.(直角三角形定义)
结论:有两个角互余的三角形是直角三角形.
练习
1.下列各组角能构成同一个三角形的三个内角的是( )
A. 34°,36°,50° B.63°,70°,67°
C. 95°,80°,5° D.25°,160°,15°
2.在△ABC中,∠A=60°,∠B=70°,则△ABC是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.无法确定
3.在△ABC中,∠A+∠B=100°,∠C=2∠B,求∠A,∠B,∠C的度数.
解:在△ABC中,
∠C=180°-(∠A+∠B)=80°,
∠B= ∠C=40°,
∠A=100°-∠B=60°
练习
应用提高
1. 如图,在△ABC 中, ∠BAC =40°, ∠B =
75°,AD 是△ABC 的角平分线.求∠ADB 的度数.
解:∵AD平分∠CAB,∠BAC=40°,
∴∠DAB= ∠BAC=20°,
在△ABD 中,
∵∠B=75°,
∴∠ADB=180°-∠B-∠BAD
=180°-20°-75°=85°.
C
B
D
A
应用提高
2. 如图,C 岛在A 岛的北偏东50°方向,B 岛
在A 岛的北偏东80°方向,C 岛在B 岛的北偏西40°方
向.从B 岛看A,C 两岛的视角∠ABC 是多少度?从C
岛看A,B 两岛的视角∠ACB 呢?
解:∠CAB=∠BAD ∠CAD
=80° 50°=30°,
∵AD∥BE,
∴∠BAD+∠ABE=180°,
应用提高
∴∠ABE=180°-∠BAD
=180° 80°=100°
∠ABC=∠ABE-∠EBC
=100° 40°=60°
在△ABC 中,
∠ACB=180° ∠ABC ∠CAB
=180° 60° 30°=90°
答:从B岛看A,C两岛的视角∠ABC是60°,从C岛看A,B两岛的视角∠ACB是90°.
体验收获
今天我们学习了哪些知识?
1.说一说三角形内角和定理?
2.怎样证明三角形内角和定理?
下课休息
