人教版九年级数学上册22.3实际问题与二次函数同步训练(word版含答案)
文档属性
| 名称 | 人教版九年级数学上册22.3实际问题与二次函数同步训练(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 177.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-04 12:13:11 | ||
图片预览


文档简介
人教版九年级数学上册22.3实际问题与二次函数同步训练
一、单选题
1.地面上一个小球被推开后笔直滑行,滑行的距离s与时间t的函数关系如图中的部分抛物线所示(其中P是该抛物线的顶点),则下列说法正确的是( )
A.小球滑行12秒停止 B.小球滑行6秒停止
C.小球滑行6秒回到起点 D.小球滑行12秒回到起点
2.地面竖直向上抛出一小球,小球的高度单位:与小球运动时间单位:之间的函数关系如图所示下列结论:①小球抛出秒时速度为;②小球在空中经过的路程是;③小球的高度时,;④小球抛出秒后,速度越来越快其中正确的是( )
A.①② B.①④ C.①②④ D.②③
3.已知学校航模组设计制作的火箭升空高度h(m)与飞行时间t(s)满足函数表达式h=﹣t2+24t+1,则下列说法中正确的是( )
A.点火后1s和点火后3s的升空高度相同
B.点火后24s火箭落于地面
C.火箭升空的最大高度为145m
D.点火后10s的升空高度为139m
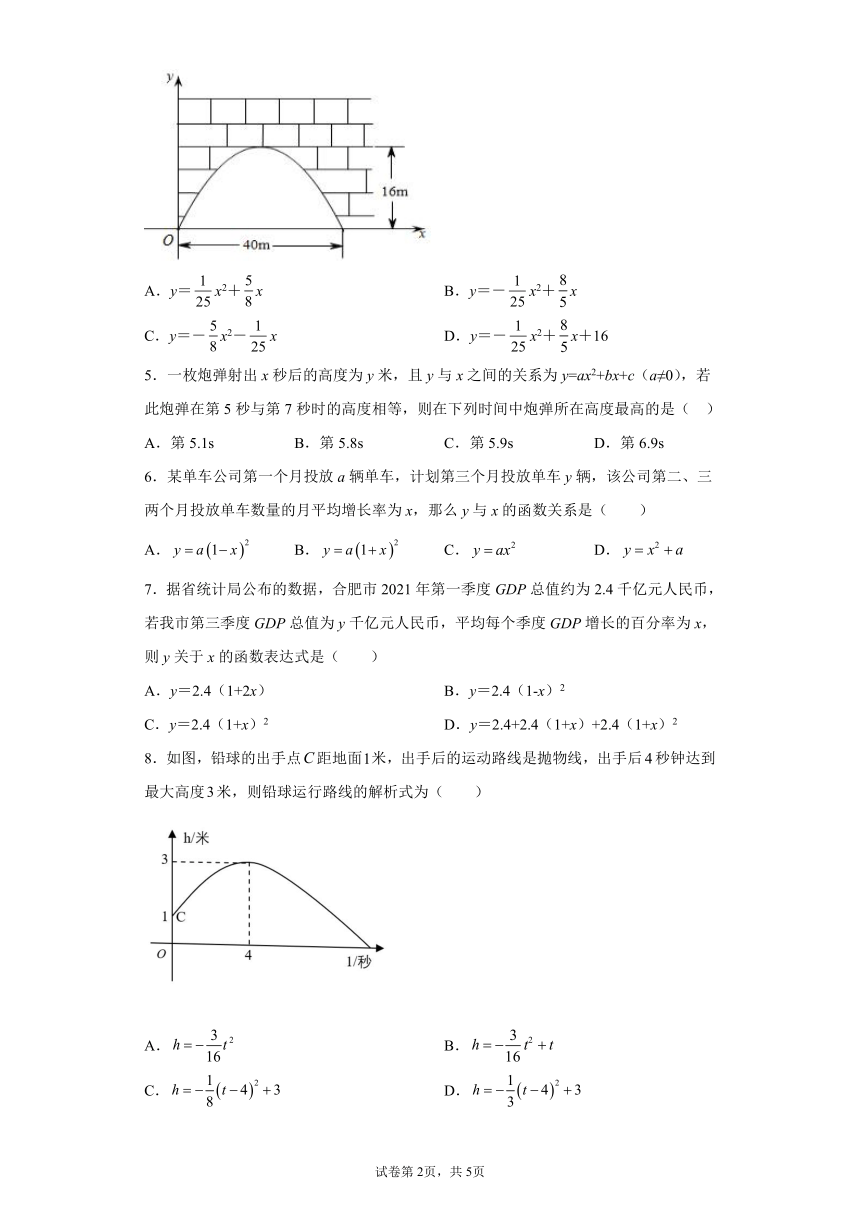
4.有一拱桥洞呈抛物线形,这个桥洞的最大高度是16m,跨度为40m,现把它的示意图(如图)放在坐标系中,则抛物线的解析式为( )
A.y=x2+x B.y=-x2+x
C.y=-x2-x D.y=-x2+x+16
5.一枚炮弹射出x秒后的高度为y米,且y与x之间的关系为y=ax2+bx+c(a≠0),若此炮弹在第5秒与第7秒时的高度相等,则在下列时间中炮弹所在高度最高的是( )
A.第5.1s B.第5.8s C.第5.9s D.第6.9s
6.某单车公司第一个月投放a辆单车,计划第三个月投放单车y辆,该公司第二、三两个月投放单车数量的月平均增长率为x,那么y与x的函数关系是( )
A. B. C. D.
7.据省统计局公布的数据,合肥市2021年第一季度GDP总值约为2.4千亿元人民币,若我市第三季度GDP总值为y千亿元人民币,平均每个季度GDP增长的百分率为x,则y关于x的函数表达式是( )
A.y=2.4(1+2x) B.y=2.4(1-x)2
C.y=2.4(1+x)2 D.y=2.4+2.4(1+x)+2.4(1+x)2
8.如图,铅球的出手点距地面米,出手后的运动路线是抛物线,出手后秒钟达到最大高度米,则铅球运行路线的解析式为( )
A. B.
C. D.
二、填空题
9.某超市购进一批单价为8元的生活用品,如果按每件9元出售,那么每天可销售20件.经调查发现,这种生活用品的销售单价每提高1元,其销售量相应减少4件,那么将销售价定为__________元时,才能使每天所获销售利润最大.
10.如图,用一段长为10米的篱笆围成一个一边靠墙(墙的长度不限)的长方形菜园,设为米,则菜园的面积(平方米)与(米)的关系式为______.(不要求写出自变量的取值范围)
11.学校准备建一个矩形花圃,其中一边靠墙,另外三边用周长为30米的篱笆围成,已知墙长为18米,设花圃垂直于墙的一边长为x米,花圃的面积为y平方米,写出y与x的函数关系式,并写出自变量x的取值范围________.
12.某种商品每件的进价为20元,调查表明:在某段时间内若以每件x元(20 ≤x ≤30)出售,可卖出(600-20x)件,为使利润最大,则每件售价应定为________元.
13.进价为80元的某衬衣定价为100元时,每月可卖出2000件,价格每上涨1元,销售量便减少5件,那么每月售出衬衣的总件数y(件)与衬衣售价x(元)之间的函数关系式为______,每月利润w(元)与衬衣售价x(元)之间的函数关系式为__________.(以上关系式只列式不化简).
14.足球被从地面上踢起,它距地面的高度h(m)可用公式h=-4.9t2+19.6t来表示,其中t(s)表示足球被踢出后经过的时间,则球在______s后落地.
15.从地面竖直向上抛射一个小球,小球的高度h (米)与运动时间t(秒)之间的关系式为h=30t﹣5t2,那么小球抛出___秒后落地.
16.如图是足球守门员在O处开出一记手抛高球后足球在空中运动到落地的过程,它是一条经过A、M、C三点的抛物线.其中A点离地面1.4米,M点是足球运动过程中的最高点,离地面3.2米,离守门员的水平距离为6米,点C是球落地时的第一点.那么足球第一次落地点C距守门员的水平距离为___米.
三、解答题
17.某商品的进价为每件40元.当售价为每件60元时,每星期可卖出300件,现需降价处理,且经市场调查:每降价1元,每星期可多卖出20件.在确保盈利的前提下,解答下列问题:
(1)若设每件降价x元、每星期售出商品的利润为y元,请写出y与x的函数关系式,并求出自变量x的取值范围;
(2)当降价多少元时,每星期的利润最大?最大利润是多少?
18.某商场销售一批商品,经市场调研:该商品进价为每个10元,当售价为每个12元时,销售量为180个,若售价每提高1元,销售量就会减少10个,但每天需支付各种费用共200元,请回答以下问题:
(1)当商品售价为每个15元时,销售量为_______个.
(2)用表达式表示该商品销售量y(个)与售价x(元)之间的函数关系;
(3)当售价定为多少时,商场每天获得利润最大?每天的最大利润是多少?
19.在国庆期间,大润发商场新上市了一款童装,进价每件60元,现以每件100元销售,每天可售出20件.在试销售阶段发现,若每件童装降价1元,那么每天就可多售2件,设每件童装单价降价了x元.
(1)若销售单价降低5元,则该款童装每天的销售量为 件,每天利润是 元;
(2)请写出每天销售该款童装的利润y(元)与每件童装降价x(元)之间的函数关系式;
(3)当每件童装销售单价定为多少元时,商场每天可获得最大利润?最大利润是多少元?
20.某市场最近购进一批优质山药,在进价的基础上提高40元销售,每天可售出50件.根据市场调查发现:销售单价每增加2元,每天的销售量就会减少1件.设销售单价增加元,每天的销售量为件.市场管理部门规定:每件山药的利润不能超过80元.
(1)请写出关于的函数解析式(写出自变量的取值范围);
(2)当为多少时,市场每天销售这种山药可获利润2250元?
(3)求市场每天销售这种山药可获得的最大利润.
参考答案
1.B
2.B
3.C
4.B
5.C
6.B
7.C
8.C
9.11
10.y=-2x2+10x
11.y=﹣2x2+30x(6≤x<15)
12.25
13.y=2000-5(x-100) w=[2000-5(x-100)](x-80)
14.4
15.6
16.14
17.(1)y=﹣20x2+100x+6000,0≤x<20(或0<x<20);(2)当降价2.5元时,利润最大且为6125元.
18.(1);(2);(3)当售价定为元时,商场每天获得利润最大,为元
19.(1)30,1050;(2)y=﹣2x2+60x+800;(3)当每件童装销售单价定为85元时,商场每天可获得最大利润,最大利润是1250元
20.(1),;(2)当x=10时,市场每天销售这种山药可获利润2250元;(3)当x=30时,市场每天销售这种山药可获得的最大利润是2450元.
试卷第4页,共5页
试卷第5页,共5页
一、单选题
1.地面上一个小球被推开后笔直滑行,滑行的距离s与时间t的函数关系如图中的部分抛物线所示(其中P是该抛物线的顶点),则下列说法正确的是( )
A.小球滑行12秒停止 B.小球滑行6秒停止
C.小球滑行6秒回到起点 D.小球滑行12秒回到起点
2.地面竖直向上抛出一小球,小球的高度单位:与小球运动时间单位:之间的函数关系如图所示下列结论:①小球抛出秒时速度为;②小球在空中经过的路程是;③小球的高度时,;④小球抛出秒后,速度越来越快其中正确的是( )
A.①② B.①④ C.①②④ D.②③
3.已知学校航模组设计制作的火箭升空高度h(m)与飞行时间t(s)满足函数表达式h=﹣t2+24t+1,则下列说法中正确的是( )
A.点火后1s和点火后3s的升空高度相同
B.点火后24s火箭落于地面
C.火箭升空的最大高度为145m
D.点火后10s的升空高度为139m
4.有一拱桥洞呈抛物线形,这个桥洞的最大高度是16m,跨度为40m,现把它的示意图(如图)放在坐标系中,则抛物线的解析式为( )
A.y=x2+x B.y=-x2+x
C.y=-x2-x D.y=-x2+x+16
5.一枚炮弹射出x秒后的高度为y米,且y与x之间的关系为y=ax2+bx+c(a≠0),若此炮弹在第5秒与第7秒时的高度相等,则在下列时间中炮弹所在高度最高的是( )
A.第5.1s B.第5.8s C.第5.9s D.第6.9s
6.某单车公司第一个月投放a辆单车,计划第三个月投放单车y辆,该公司第二、三两个月投放单车数量的月平均增长率为x,那么y与x的函数关系是( )
A. B. C. D.
7.据省统计局公布的数据,合肥市2021年第一季度GDP总值约为2.4千亿元人民币,若我市第三季度GDP总值为y千亿元人民币,平均每个季度GDP增长的百分率为x,则y关于x的函数表达式是( )
A.y=2.4(1+2x) B.y=2.4(1-x)2
C.y=2.4(1+x)2 D.y=2.4+2.4(1+x)+2.4(1+x)2
8.如图,铅球的出手点距地面米,出手后的运动路线是抛物线,出手后秒钟达到最大高度米,则铅球运行路线的解析式为( )
A. B.
C. D.
二、填空题
9.某超市购进一批单价为8元的生活用品,如果按每件9元出售,那么每天可销售20件.经调查发现,这种生活用品的销售单价每提高1元,其销售量相应减少4件,那么将销售价定为__________元时,才能使每天所获销售利润最大.
10.如图,用一段长为10米的篱笆围成一个一边靠墙(墙的长度不限)的长方形菜园,设为米,则菜园的面积(平方米)与(米)的关系式为______.(不要求写出自变量的取值范围)
11.学校准备建一个矩形花圃,其中一边靠墙,另外三边用周长为30米的篱笆围成,已知墙长为18米,设花圃垂直于墙的一边长为x米,花圃的面积为y平方米,写出y与x的函数关系式,并写出自变量x的取值范围________.
12.某种商品每件的进价为20元,调查表明:在某段时间内若以每件x元(20 ≤x ≤30)出售,可卖出(600-20x)件,为使利润最大,则每件售价应定为________元.
13.进价为80元的某衬衣定价为100元时,每月可卖出2000件,价格每上涨1元,销售量便减少5件,那么每月售出衬衣的总件数y(件)与衬衣售价x(元)之间的函数关系式为______,每月利润w(元)与衬衣售价x(元)之间的函数关系式为__________.(以上关系式只列式不化简).
14.足球被从地面上踢起,它距地面的高度h(m)可用公式h=-4.9t2+19.6t来表示,其中t(s)表示足球被踢出后经过的时间,则球在______s后落地.
15.从地面竖直向上抛射一个小球,小球的高度h (米)与运动时间t(秒)之间的关系式为h=30t﹣5t2,那么小球抛出___秒后落地.
16.如图是足球守门员在O处开出一记手抛高球后足球在空中运动到落地的过程,它是一条经过A、M、C三点的抛物线.其中A点离地面1.4米,M点是足球运动过程中的最高点,离地面3.2米,离守门员的水平距离为6米,点C是球落地时的第一点.那么足球第一次落地点C距守门员的水平距离为___米.
三、解答题
17.某商品的进价为每件40元.当售价为每件60元时,每星期可卖出300件,现需降价处理,且经市场调查:每降价1元,每星期可多卖出20件.在确保盈利的前提下,解答下列问题:
(1)若设每件降价x元、每星期售出商品的利润为y元,请写出y与x的函数关系式,并求出自变量x的取值范围;
(2)当降价多少元时,每星期的利润最大?最大利润是多少?
18.某商场销售一批商品,经市场调研:该商品进价为每个10元,当售价为每个12元时,销售量为180个,若售价每提高1元,销售量就会减少10个,但每天需支付各种费用共200元,请回答以下问题:
(1)当商品售价为每个15元时,销售量为_______个.
(2)用表达式表示该商品销售量y(个)与售价x(元)之间的函数关系;
(3)当售价定为多少时,商场每天获得利润最大?每天的最大利润是多少?
19.在国庆期间,大润发商场新上市了一款童装,进价每件60元,现以每件100元销售,每天可售出20件.在试销售阶段发现,若每件童装降价1元,那么每天就可多售2件,设每件童装单价降价了x元.
(1)若销售单价降低5元,则该款童装每天的销售量为 件,每天利润是 元;
(2)请写出每天销售该款童装的利润y(元)与每件童装降价x(元)之间的函数关系式;
(3)当每件童装销售单价定为多少元时,商场每天可获得最大利润?最大利润是多少元?
20.某市场最近购进一批优质山药,在进价的基础上提高40元销售,每天可售出50件.根据市场调查发现:销售单价每增加2元,每天的销售量就会减少1件.设销售单价增加元,每天的销售量为件.市场管理部门规定:每件山药的利润不能超过80元.
(1)请写出关于的函数解析式(写出自变量的取值范围);
(2)当为多少时,市场每天销售这种山药可获利润2250元?
(3)求市场每天销售这种山药可获得的最大利润.
参考答案
1.B
2.B
3.C
4.B
5.C
6.B
7.C
8.C
9.11
10.y=-2x2+10x
11.y=﹣2x2+30x(6≤x<15)
12.25
13.y=2000-5(x-100) w=[2000-5(x-100)](x-80)
14.4
15.6
16.14
17.(1)y=﹣20x2+100x+6000,0≤x<20(或0<x<20);(2)当降价2.5元时,利润最大且为6125元.
18.(1);(2);(3)当售价定为元时,商场每天获得利润最大,为元
19.(1)30,1050;(2)y=﹣2x2+60x+800;(3)当每件童装销售单价定为85元时,商场每天可获得最大利润,最大利润是1250元
20.(1),;(2)当x=10时,市场每天销售这种山药可获利润2250元;(3)当x=30时,市场每天销售这种山药可获得的最大利润是2450元.
试卷第4页,共5页
试卷第5页,共5页
同课章节目录
