2021-2022学年人教版八年级数学上册11.3.1多边形 同步课件(共22张PPT)
文档属性
| 名称 | 2021-2022学年人教版八年级数学上册11.3.1多边形 同步课件(共22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 5.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-04 10:58:54 | ||
图片预览


文档简介
(共22张PPT)
11.3.1 多边形
及其内角和
人教版 初中数学
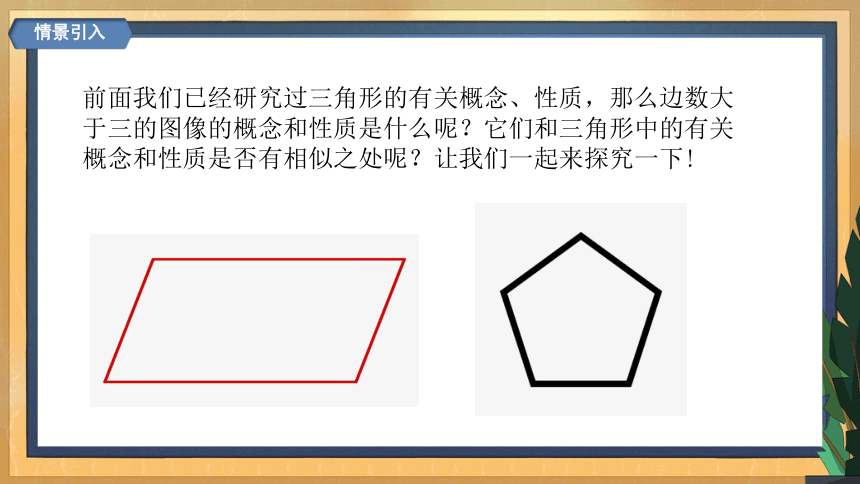
前面我们已经研究过三角形的有关概念、性质,那么边数大于三的图像的概念和性质是什么呢?它们和三角形中的有关概念和性质是否有相似之处呢?让我们一起来探究一下!
情景引入
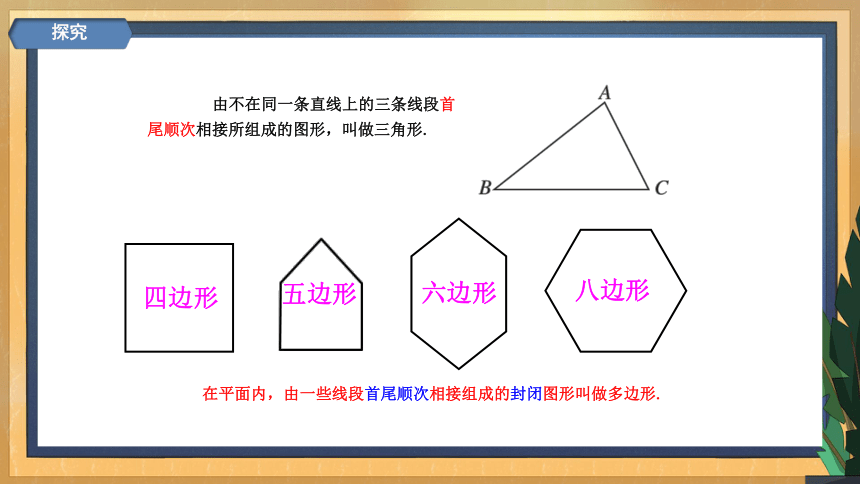
由不在同一条直线上的三条线段首尾顺次相接所组成的图形,叫做三角形.
在平面内,由一些线段首尾顺次相接组成的封闭图形叫做多边形.
四边形
五边形
六边形
八边形
探究
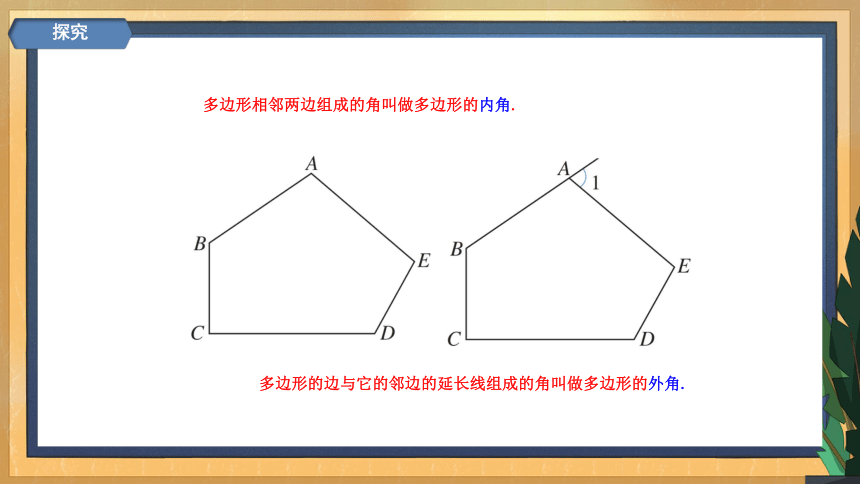
多边形相邻两边组成的角叫做多边形的内角.
多边形的边与它的邻边的延长线组成的角叫做多边形的外角.
探究
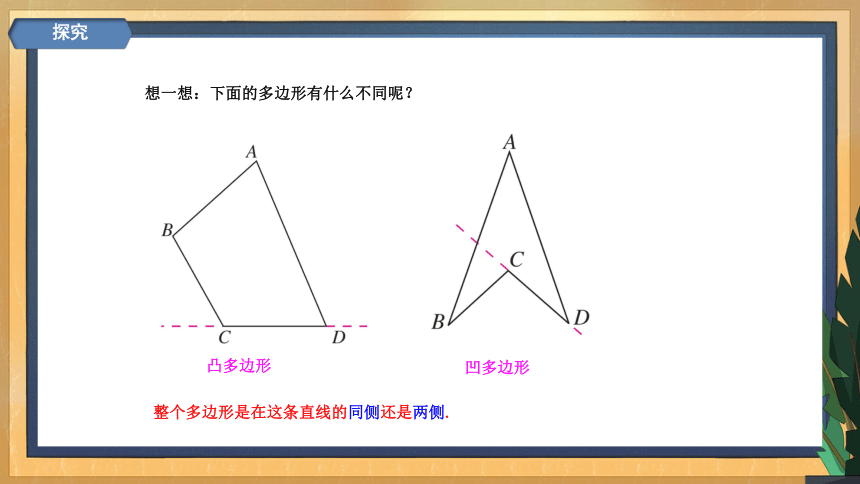
想一想:下面的多边形有什么不同呢?
凸多边形
凹多边形
整个多边形是在这条直线的同侧还是两侧.
探究
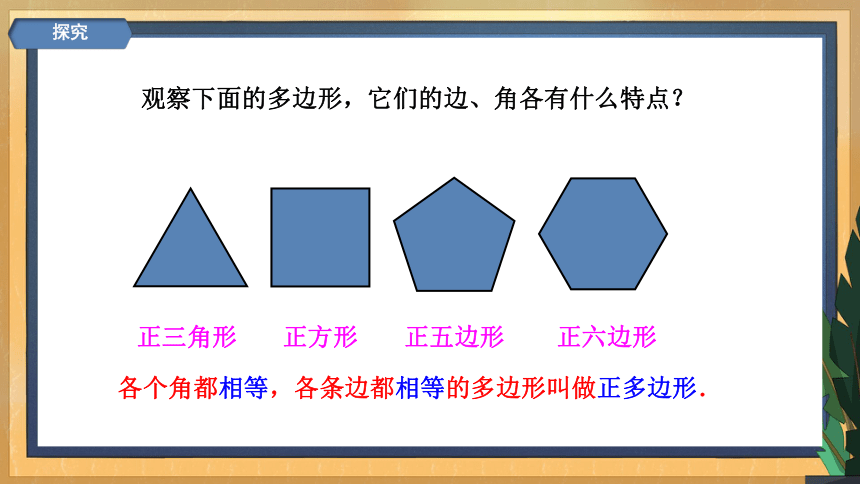
观察下面的多边形,它们的边、角各有什么特点?
各个角都相等,各条边都相等的多边形叫做正多边形.
正三角形
正方形
正五边形
正六边形
探究
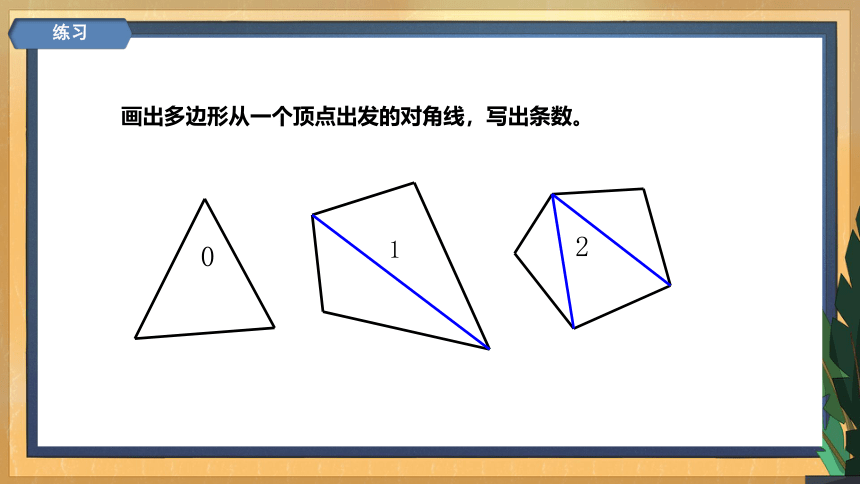
画出多边形从一个顶点出发的对角线,写出条数。
0
1
2
练习
3
你能总结出规律吗?
5
多边形从一个顶点出发的对角线的条数=n-3
练习
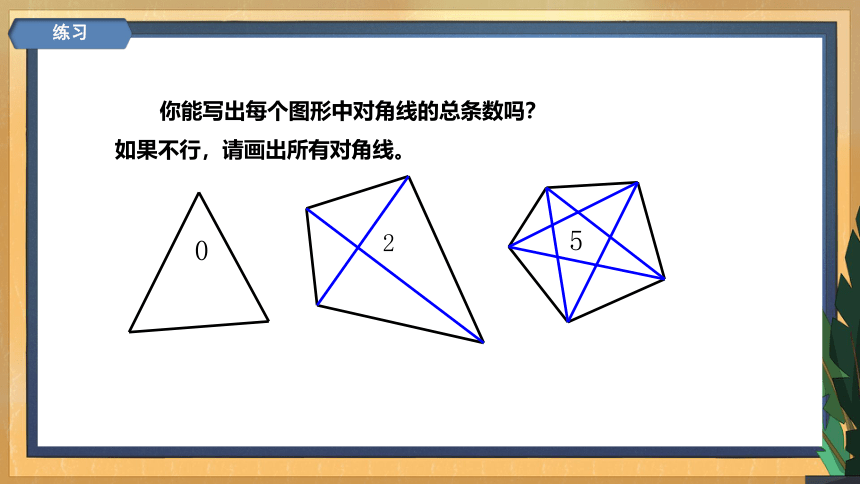
你能写出每个图形中对角线的总条数吗?
如果不行,请画出所有对角线。
0
2
5
练习
9
你能总结出多边形对角线的数量的规律吗?
20
练习
连接多边形不相邻的两个顶点的线段,叫做多边形的对角线.
你能画出
其它的对角
线吗?
n边形的一个顶点能引出(n-3)条对角线,把这个多边形分成(n-2)个三角形
归纳
解析:根据正多边形的概念得:
A、各边相等,各角也相等的多边形叫做正多边形,故错误;
B、各边相等,各角也相等的多边形叫做正多边形,故错误;
C、既是轴对称图形又是中心对称图形的多边形是正多边形,错误,如菱形;
D、符合正多边形的定义,正确.故选D.
1.下列命题正确的是( )
A.各边相等的多边形是正多边形
B.各内角分别相等的多边形是正多边形
C.既是轴对称图形又是中心对称图形的多边形是正多边形
D.各边相等,各角也相等的多边形是正多边形
D
应用提高
解析:从n边形的一个顶点出发可引出(n-3)条对角线,可组成(n-2)个三角形,
即可得n-2=10,
解得:n=12.
故选C.
2.过一个多边形的一个顶点的所有对角线把多边形分成10个三角形,则这个多边形的边数是( )
A.10 B.11 C.12 D.13
C
应用提高
3.如图所示,①中多边形(边数为12)是由正三角形“扩展”而来的,②中多边形是由正方形“扩展”而来的,…,依此类推,则由正八边形“扩展”而来的多边形的边数为( )
A.32 B.40
C.72 D.64
C
应用提高
解析:∵①正三边形“扩展”而来的多边形的边数是12=3×4,
②正四边形“扩展”而来的多边形的边数是20=4×5,
③正五边形“扩展”而来的多边形的边数为30=5×6,
④正六边形“扩展”而来的多边形的边数为42=6×7,
∴正n边形“扩展”而来的多边形的边数为n(n+1).
当n=8时,8(8+1)=72个,
故选C
应用提高
4.图所示,写出这些多边形的名称,并从多边形的一个顶点出发到其他顶点把多边形分割成若干个三角形.
应用提高
(1)四边形,分割如图(1):
(2)五边形,分割如图(2):
(3)七边形,分割如图(3):
应用提高
5.同学们,你们会用画多边形的对角线来解决生活中的数学问题吗?
比如,学校举办足球赛,共有5个班级的足球队参加比赛,每个队都要和其他各队比赛一场,根据积分排列名次.问学校一共要安排多少场比赛?
我们画出5个点,每个点各代表一个足球队,两个队之间比赛一场就用一条线段把它们连接起来.由于每个队都要与其他各队比赛一场,这样每个点与另外4个点都会有一条线段连接(如右图).
现在我们只要数一数五边形的边数和它的对角线条数就可以了.由图可知,五边形的边数和对角线条数都是5,所以学校一共要安排10场比赛.
同学们,请用类似的方法来解决下面的问题:
姣姣、林林、可可、飞飞、红红和娜娜六人参加一次会议,见面时他们相互握手问好.已知姣姣已握了5次手,林林已握了4次手,可可已握了3次手,飞飞已握了2次手,红红握手1次,请推算出娜娜目前已和哪几个人握了手。
应用提高
解析:先画出6个点,A、B、C、D、E、F各个点依次代表姣姣、林林、可可、飞飞、红红和娜娜,凡是两人之间握过手,就把代表他们的这两点用1条线段连接起来(如图所示)。
先看姣姣(A)和红红(E).姣姣已握手5次,说明姣姣与另外5人都握了手,因此代表姣姣的A点与B、C、D、E、F这5点都有一条线段连接;红红握手1次,他只能是与姣姣握的手了,所以E点只能与A点之间有线段连接,与其它各点再也不能有线段连接了.
其次分析林林(B).林林已握手4次,由于他没有可能与红红握过手,所以只能是与剩下的四个人姣姣、可可、飞飞和娜娜握过手了,因此,点B与A、C、D、F四点之间有线段连接.
应用提高
再看飞飞(D).飞飞已握手2次,而代表飞飞的D点已与A、B两点有线段连接了,所以D点与其它的点不能再有线段连接了.
最后考察可可(C).可可与3人握了手,但已不能是与飞飞和红红握的手了,所以代表可可的点C只能与A、B、F三点有线段连接.
现在观察图形,与代表娜娜的点连接的线段有3条(AF、BF和CF),这说明姣姣、林林和可可三人已与娜娜握过手.
应用提高
教材21页练习第1、2题.
布置作业
下课休息
11.3.1 多边形
及其内角和
人教版 初中数学
前面我们已经研究过三角形的有关概念、性质,那么边数大于三的图像的概念和性质是什么呢?它们和三角形中的有关概念和性质是否有相似之处呢?让我们一起来探究一下!
情景引入
由不在同一条直线上的三条线段首尾顺次相接所组成的图形,叫做三角形.
在平面内,由一些线段首尾顺次相接组成的封闭图形叫做多边形.
四边形
五边形
六边形
八边形
探究
多边形相邻两边组成的角叫做多边形的内角.
多边形的边与它的邻边的延长线组成的角叫做多边形的外角.
探究
想一想:下面的多边形有什么不同呢?
凸多边形
凹多边形
整个多边形是在这条直线的同侧还是两侧.
探究
观察下面的多边形,它们的边、角各有什么特点?
各个角都相等,各条边都相等的多边形叫做正多边形.
正三角形
正方形
正五边形
正六边形
探究
画出多边形从一个顶点出发的对角线,写出条数。
0
1
2
练习
3
你能总结出规律吗?
5
多边形从一个顶点出发的对角线的条数=n-3
练习
你能写出每个图形中对角线的总条数吗?
如果不行,请画出所有对角线。
0
2
5
练习
9
你能总结出多边形对角线的数量的规律吗?
20
练习
连接多边形不相邻的两个顶点的线段,叫做多边形的对角线.
你能画出
其它的对角
线吗?
n边形的一个顶点能引出(n-3)条对角线,把这个多边形分成(n-2)个三角形
归纳
解析:根据正多边形的概念得:
A、各边相等,各角也相等的多边形叫做正多边形,故错误;
B、各边相等,各角也相等的多边形叫做正多边形,故错误;
C、既是轴对称图形又是中心对称图形的多边形是正多边形,错误,如菱形;
D、符合正多边形的定义,正确.故选D.
1.下列命题正确的是( )
A.各边相等的多边形是正多边形
B.各内角分别相等的多边形是正多边形
C.既是轴对称图形又是中心对称图形的多边形是正多边形
D.各边相等,各角也相等的多边形是正多边形
D
应用提高
解析:从n边形的一个顶点出发可引出(n-3)条对角线,可组成(n-2)个三角形,
即可得n-2=10,
解得:n=12.
故选C.
2.过一个多边形的一个顶点的所有对角线把多边形分成10个三角形,则这个多边形的边数是( )
A.10 B.11 C.12 D.13
C
应用提高
3.如图所示,①中多边形(边数为12)是由正三角形“扩展”而来的,②中多边形是由正方形“扩展”而来的,…,依此类推,则由正八边形“扩展”而来的多边形的边数为( )
A.32 B.40
C.72 D.64
C
应用提高
解析:∵①正三边形“扩展”而来的多边形的边数是12=3×4,
②正四边形“扩展”而来的多边形的边数是20=4×5,
③正五边形“扩展”而来的多边形的边数为30=5×6,
④正六边形“扩展”而来的多边形的边数为42=6×7,
∴正n边形“扩展”而来的多边形的边数为n(n+1).
当n=8时,8(8+1)=72个,
故选C
应用提高
4.图所示,写出这些多边形的名称,并从多边形的一个顶点出发到其他顶点把多边形分割成若干个三角形.
应用提高
(1)四边形,分割如图(1):
(2)五边形,分割如图(2):
(3)七边形,分割如图(3):
应用提高
5.同学们,你们会用画多边形的对角线来解决生活中的数学问题吗?
比如,学校举办足球赛,共有5个班级的足球队参加比赛,每个队都要和其他各队比赛一场,根据积分排列名次.问学校一共要安排多少场比赛?
我们画出5个点,每个点各代表一个足球队,两个队之间比赛一场就用一条线段把它们连接起来.由于每个队都要与其他各队比赛一场,这样每个点与另外4个点都会有一条线段连接(如右图).
现在我们只要数一数五边形的边数和它的对角线条数就可以了.由图可知,五边形的边数和对角线条数都是5,所以学校一共要安排10场比赛.
同学们,请用类似的方法来解决下面的问题:
姣姣、林林、可可、飞飞、红红和娜娜六人参加一次会议,见面时他们相互握手问好.已知姣姣已握了5次手,林林已握了4次手,可可已握了3次手,飞飞已握了2次手,红红握手1次,请推算出娜娜目前已和哪几个人握了手。
应用提高
解析:先画出6个点,A、B、C、D、E、F各个点依次代表姣姣、林林、可可、飞飞、红红和娜娜,凡是两人之间握过手,就把代表他们的这两点用1条线段连接起来(如图所示)。
先看姣姣(A)和红红(E).姣姣已握手5次,说明姣姣与另外5人都握了手,因此代表姣姣的A点与B、C、D、E、F这5点都有一条线段连接;红红握手1次,他只能是与姣姣握的手了,所以E点只能与A点之间有线段连接,与其它各点再也不能有线段连接了.
其次分析林林(B).林林已握手4次,由于他没有可能与红红握过手,所以只能是与剩下的四个人姣姣、可可、飞飞和娜娜握过手了,因此,点B与A、C、D、F四点之间有线段连接.
应用提高
再看飞飞(D).飞飞已握手2次,而代表飞飞的D点已与A、B两点有线段连接了,所以D点与其它的点不能再有线段连接了.
最后考察可可(C).可可与3人握了手,但已不能是与飞飞和红红握的手了,所以代表可可的点C只能与A、B、F三点有线段连接.
现在观察图形,与代表娜娜的点连接的线段有3条(AF、BF和CF),这说明姣姣、林林和可可三人已与娜娜握过手.
应用提高
教材21页练习第1、2题.
布置作业
下课休息
