人教版九年级数学上册22.3实际问题与二次函数练习(word版、含答案)
文档属性
| 名称 | 人教版九年级数学上册22.3实际问题与二次函数练习(word版、含答案) | 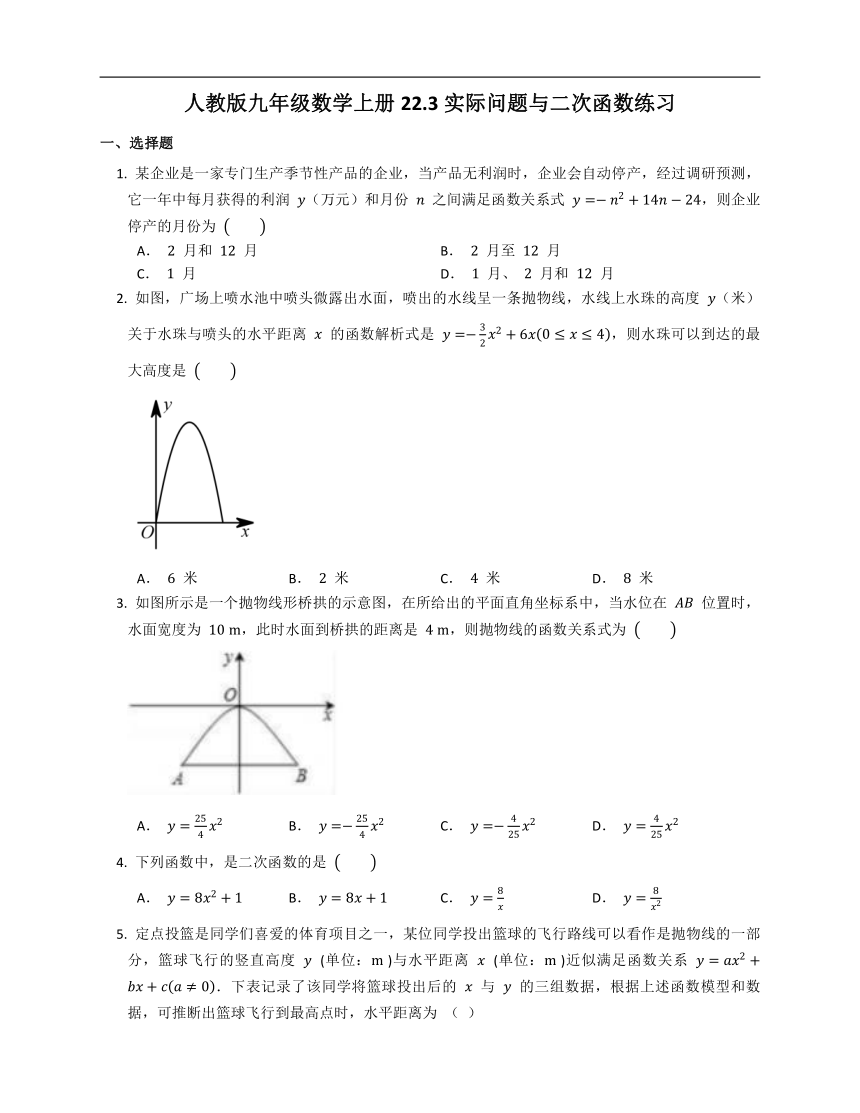 | |
| 格式 | docx | ||
| 文件大小 | 120.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-04 17:19:25 | ||
图片预览


文档简介
人教版九年级数学上册22.3实际问题与二次函数练习
一、选择题
某企业是一家专门生产季节性产品的企业,当产品无利润时,企业会自动停产,经过调研预测,它一年中每月获得的利润 (万元)和月份 之间满足函数关系式 ,则企业停产的月份为
A. 月和 月 B. 月至 月
C. 月 D. 月、 月和 月
如图,广场上喷水池中喷头微露出水面,喷出的水线呈一条抛物线,水线上水珠的高度 (米)关于水珠与喷头的水平距离 的函数解析式是 ,则水珠可以到达的最大高度是
A. 米 B. 米 C. 米 D. 米
如图所示是一个抛物线形桥拱的示意图,在所给出的平面直角坐标系中,当水位在 位置时,水面宽度为 ,此时水面到桥拱的距离是 ,则抛物线的函数关系式为
A. B. C. D.
下列函数中,是二次函数的是
A. B. C. D.
定点投篮是同学们喜爱的体育项目之一,某位同学投出篮球的飞行路线可以看作是抛物线的一部分,篮球飞行的竖直高度 (单位: )与水平距离 (单位: )近似满足函数关系 .下表记录了该同学将篮球投出后的 与 的三组数据,根据上述函数模型和数据,可推断出篮球飞行到最高点时,水平距离为 ( )
A. B. C. D.
要得到 的图象,需将抛物线 作如下平移
A.先向右平移 个单位长度,再向上平移 个单位长度
B.先向右平移 个单位长度,再向下平移 个单位长度
C.先向左平移 个单位长度,再向上平移 个单位长度
D.先向左平移 个单位长度,再向下平移 个单位长度
某种品牌的服装进价为每件 元,当售价为每件 元时,每天可卖出 件,现需降价处理,且经市场调查:每件服装每降价 元,每天可多卖出 件.在确保盈利的前提下,若设每件服装降价 元,每天售出服装的利润为 元,则 与 的函数关系式为
A.
B.
C.
D.
抛物线 的开口方向和顶点坐标分别是
A.向下, B.向下,
C.向上, D.向上,
二、填空题
函数 的图象是 ,对称轴是 ,顶点是 .
当 时,二次函数 有最小值 .
已知关于 的方程 是一元二次方程的条件是 .
已知一个正方形的面积为 ,当边长增加 时,正方形的面积变为 ,则原正方形的边长为 ,边长增加 后变为 ,所以 关于 的函数关系式为 .
用 米长的绳子围成的最大矩形面积为 .
二次函数 与 轴有公共点,则 ;若一元二次方程 的两根为 ,,则二次函数 可表示为 .
用长度一定的绳子围成一个矩形,如果矩形的一边长 与面积 满足函数解析式 ,那么该矩形面积的最大值为 .
用长为 米的铁丝围成一个长方形,如果长方形的一边长为 米,面积为 平方米,那么 与 的函数解析式为 .
三、解答题
现有一面 米长的墙,某农户计划用 米长的篱笆靠墙围成一个矩形养鸡场 (篱笆只围 ,, 三边),其示意图如图所示.
(参考数据:,,)
(1) 若矩形养鸡场的面积为 平方米,求所用的墙长 ;(结果精确到 米)
(2) 求此矩形养鸡场的最大面积.
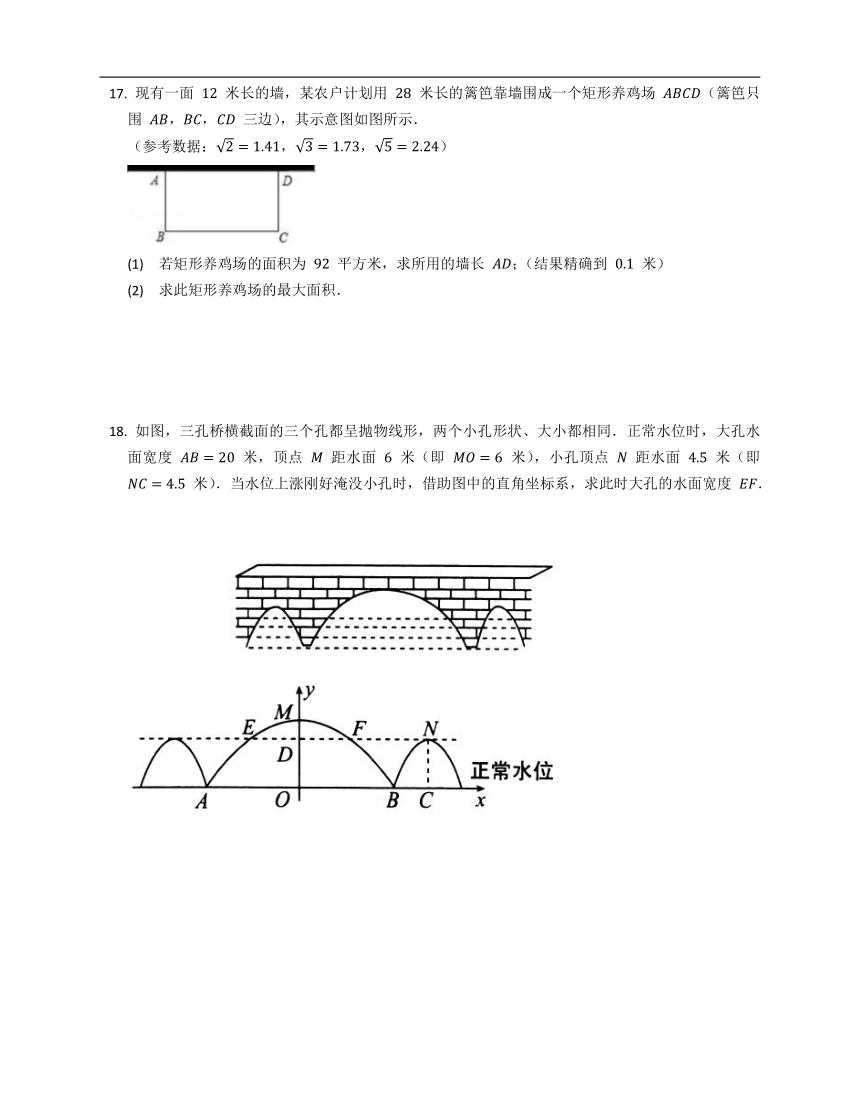
如图,三孔桥横截面的三个孔都呈抛物线形,两个小孔形状、大小都相同.正常水位时,大孔水面宽度 米,顶点 距水面 米(即 米),小孔顶点 距水面 米(即 米).当水位上涨刚好淹没小孔时,借助图中的直角坐标系,求此时大孔的水面宽度 .
一个批发商销售成本为 元/千克的某产品,根据物价部门规定:该产品每千克售价不得超过 元,在销售过程中发现的售量 (千克)与售价 (元/千克)满足一次函数关系,对应关系如下表:
(1) 求 与 的函数关系式;
(2) 该批发商若想获得 元的利润,应将售价定为多少元?
(3) 该产品每千克售价为多少元时,批发商获得的利润 (元)最大?此时的最大利润为多少元?
某校准备围建一个矩形苗圃园,其中一边靠墙,且墙长为 ,另外三边用周长为 的篱笆围成,设苗圃园垂直于墙的一边长为 ,苗圃园的面积为 .
(1) 求 与 之间的函数关系式.
(2) 求 的最大值.
答案
一、选择题
1. 【答案】D
2. 【答案】A
3. 【答案】C
4. 【答案】A
5. 【答案】C
6. 【答案】D
7. 【答案】A
8. 【答案】B
二、填空题
9. 【答案】一条抛物线; 轴;
10. 【答案】 ;
11. 【答案】
12. 【答案】 ; ;
13. 【答案】
14. 【答案】;
15. 【答案】
16. 【答案】
三、解答题
17. 【答案】
(1) 设 米,则 米,
根据题意,得:,
解得:,不合题意,舍去.
,
答:所用的墙长 约为 米.
(2) 设矩形养鸡场 的面积为 平方米,则:
,
墙长 米,
,
当 时, 取最大值为:,
答:此矩形养鸡场的最大面积为 平方米.
18. 【答案】设大孔所在抛物线的解析式为 ,依题意得 . ,解得 ,即 .当 时,有 ,解得 ,,,即水面宽度为 米.
19. 【答案】
(1) 设 与 的函数关系式为 ,
根据题意得
解得
故 与 的函数关系式为 .
(2) 根据题意得解得 ,(不合题意,舍去).
故该批发商若想获得 元的利润,应将售价定为 元.
(3) 与 的函数关系式为:
,
当 时, 值最大, 最大值是 .
该产品每千克售价为 元时,批发商获得的利润 (元)最大,此时的最大利润为 元.
20. 【答案】
(1) ,
墙长 米,
,,
.
(2)
抛物线开口向下,对称轴是直线 ,
在对称轴右侧 随 的增大而减小,
当 时, 有最大值,最大值为 .
一、选择题
某企业是一家专门生产季节性产品的企业,当产品无利润时,企业会自动停产,经过调研预测,它一年中每月获得的利润 (万元)和月份 之间满足函数关系式 ,则企业停产的月份为
A. 月和 月 B. 月至 月
C. 月 D. 月、 月和 月
如图,广场上喷水池中喷头微露出水面,喷出的水线呈一条抛物线,水线上水珠的高度 (米)关于水珠与喷头的水平距离 的函数解析式是 ,则水珠可以到达的最大高度是
A. 米 B. 米 C. 米 D. 米
如图所示是一个抛物线形桥拱的示意图,在所给出的平面直角坐标系中,当水位在 位置时,水面宽度为 ,此时水面到桥拱的距离是 ,则抛物线的函数关系式为
A. B. C. D.
下列函数中,是二次函数的是
A. B. C. D.
定点投篮是同学们喜爱的体育项目之一,某位同学投出篮球的飞行路线可以看作是抛物线的一部分,篮球飞行的竖直高度 (单位: )与水平距离 (单位: )近似满足函数关系 .下表记录了该同学将篮球投出后的 与 的三组数据,根据上述函数模型和数据,可推断出篮球飞行到最高点时,水平距离为 ( )
A. B. C. D.
要得到 的图象,需将抛物线 作如下平移
A.先向右平移 个单位长度,再向上平移 个单位长度
B.先向右平移 个单位长度,再向下平移 个单位长度
C.先向左平移 个单位长度,再向上平移 个单位长度
D.先向左平移 个单位长度,再向下平移 个单位长度
某种品牌的服装进价为每件 元,当售价为每件 元时,每天可卖出 件,现需降价处理,且经市场调查:每件服装每降价 元,每天可多卖出 件.在确保盈利的前提下,若设每件服装降价 元,每天售出服装的利润为 元,则 与 的函数关系式为
A.
B.
C.
D.
抛物线 的开口方向和顶点坐标分别是
A.向下, B.向下,
C.向上, D.向上,
二、填空题
函数 的图象是 ,对称轴是 ,顶点是 .
当 时,二次函数 有最小值 .
已知关于 的方程 是一元二次方程的条件是 .
已知一个正方形的面积为 ,当边长增加 时,正方形的面积变为 ,则原正方形的边长为 ,边长增加 后变为 ,所以 关于 的函数关系式为 .
用 米长的绳子围成的最大矩形面积为 .
二次函数 与 轴有公共点,则 ;若一元二次方程 的两根为 ,,则二次函数 可表示为 .
用长度一定的绳子围成一个矩形,如果矩形的一边长 与面积 满足函数解析式 ,那么该矩形面积的最大值为 .
用长为 米的铁丝围成一个长方形,如果长方形的一边长为 米,面积为 平方米,那么 与 的函数解析式为 .
三、解答题
现有一面 米长的墙,某农户计划用 米长的篱笆靠墙围成一个矩形养鸡场 (篱笆只围 ,, 三边),其示意图如图所示.
(参考数据:,,)
(1) 若矩形养鸡场的面积为 平方米,求所用的墙长 ;(结果精确到 米)
(2) 求此矩形养鸡场的最大面积.
如图,三孔桥横截面的三个孔都呈抛物线形,两个小孔形状、大小都相同.正常水位时,大孔水面宽度 米,顶点 距水面 米(即 米),小孔顶点 距水面 米(即 米).当水位上涨刚好淹没小孔时,借助图中的直角坐标系,求此时大孔的水面宽度 .
一个批发商销售成本为 元/千克的某产品,根据物价部门规定:该产品每千克售价不得超过 元,在销售过程中发现的售量 (千克)与售价 (元/千克)满足一次函数关系,对应关系如下表:
(1) 求 与 的函数关系式;
(2) 该批发商若想获得 元的利润,应将售价定为多少元?
(3) 该产品每千克售价为多少元时,批发商获得的利润 (元)最大?此时的最大利润为多少元?
某校准备围建一个矩形苗圃园,其中一边靠墙,且墙长为 ,另外三边用周长为 的篱笆围成,设苗圃园垂直于墙的一边长为 ,苗圃园的面积为 .
(1) 求 与 之间的函数关系式.
(2) 求 的最大值.
答案
一、选择题
1. 【答案】D
2. 【答案】A
3. 【答案】C
4. 【答案】A
5. 【答案】C
6. 【答案】D
7. 【答案】A
8. 【答案】B
二、填空题
9. 【答案】一条抛物线; 轴;
10. 【答案】 ;
11. 【答案】
12. 【答案】 ; ;
13. 【答案】
14. 【答案】;
15. 【答案】
16. 【答案】
三、解答题
17. 【答案】
(1) 设 米,则 米,
根据题意,得:,
解得:,不合题意,舍去.
,
答:所用的墙长 约为 米.
(2) 设矩形养鸡场 的面积为 平方米,则:
,
墙长 米,
,
当 时, 取最大值为:,
答:此矩形养鸡场的最大面积为 平方米.
18. 【答案】设大孔所在抛物线的解析式为 ,依题意得 . ,解得 ,即 .当 时,有 ,解得 ,,,即水面宽度为 米.
19. 【答案】
(1) 设 与 的函数关系式为 ,
根据题意得
解得
故 与 的函数关系式为 .
(2) 根据题意得解得 ,(不合题意,舍去).
故该批发商若想获得 元的利润,应将售价定为 元.
(3) 与 的函数关系式为:
,
当 时, 值最大, 最大值是 .
该产品每千克售价为 元时,批发商获得的利润 (元)最大,此时的最大利润为 元.
20. 【答案】
(1) ,
墙长 米,
,,
.
(2)
抛物线开口向下,对称轴是直线 ,
在对称轴右侧 随 的增大而减小,
当 时, 有最大值,最大值为 .
同课章节目录
