5.1.2弧度制 课件(共20张PPT)
文档属性
| 名称 | 5.1.2弧度制 课件(共20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-05 18:57:22 | ||
图片预览







文档简介
(共20张PPT)
5.1.2弧度制
人教A(2019)版
必修一
新知导入
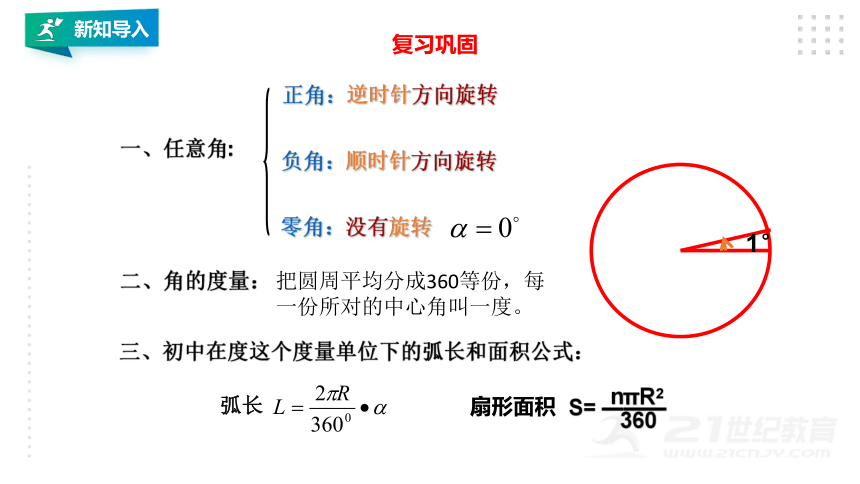
复习巩固
一、任意角:
正角:逆时针方向旋转
负角:顺时针方向旋转
零角:没有旋转
二、角的度量:
把圆周平均分成360等份,每
一份所对的中心角叫一度。
1°
三、初中在度这个度量单位下的弧长和面积公式:
nπR2
360
S= ———
弧长
扇形面积
新知讲解
角度制这种计量方法是古巴比伦人发明的,是将圆周平均分成360等份
把一份定义为一度,是一个几何概念,有明显的直观性,比如900是圆周的
四分之一,是直角;1800圆周的一半是平角等等很多特殊角的角度都是整数
等优点,但也存在明显的不足,(1)在研究以角为自变量的函数时,自变量和
函数值都应是两个实数集合,以角度计量显然不满足这个条件;(2)从前面学
过的弧长和扇形面积公式可以看出,使用角度制这些公式比较繁琐。
随着学习的不断深入,我们会发现角度制计量方法有很多不便之处,为
了解决这些问题,英国数学家罗杰·柯特斯Roger Cotes在1714年提出弧度制的
概念。
新知讲解
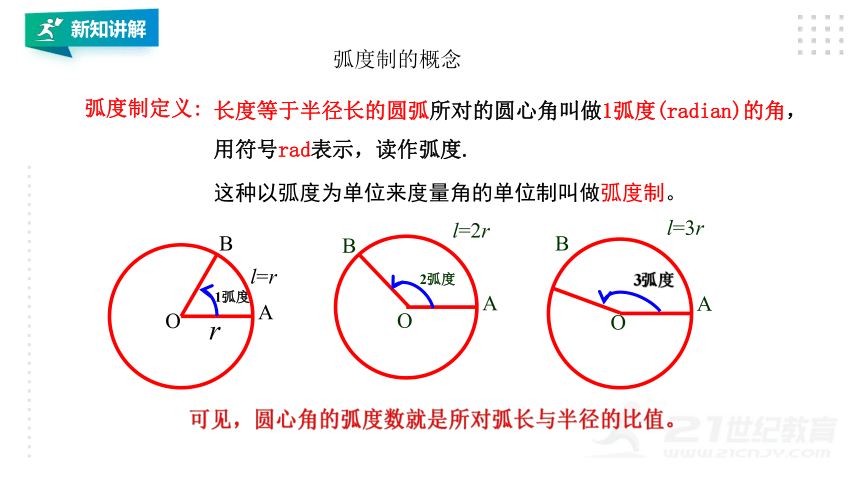
弧度制的概念
弧度制定义:
长度等于半径长的圆弧所对的圆心角叫做1弧度(radian)的角,
用符号rad表示,读作弧度.
这种以弧度为单位来度量角的单位制叫做弧度制。
1弧度
r
l=r
O
A
B
2弧度
O
A
B
l=2r
B
3弧度
O
A
l=3r
可见,圆心角的弧度数就是所对弧长与半径的比值。
新知讲解
为什么可以用弧长与其半径的比值来度量角的大小呢?即这个比值
是否与所取的圆的半径大小无关呢?
我们从初中所学的弧长公式 中可以得到答案:
将公式变形为:
我们发现如果角确定后,弧长与半径的比值是一个确定的值,而
不随弧长与半径的改变而改变。
A
B
A'
B'
一般地,我们规定:正角的弧度数为正数,负角的弧度数为负数,零角的弧度数为0,如果半径为r的圆的圆心角α所对弧的长为l,那么角α的弧度数的绝对值是
︱α︱=
l
r
α的正负由角α的终边的旋转方向决定
弧度与角度的互化
新知讲解
将角度α化为弧度数β:
由弧长公式:
将弧度 度α化为角度数β:
由弧长公式:
1°= —— 弧度 ≈ 0.01745弧度
180
π
1弧度 =( ——)°≈ 57.30°= 57°18′
π
180
3600=2π弧度
圆周的弧长l=2πr,周角3600,所以,3600=
1800=π弧度
度 00 300 450 1200 1350 1500 3600
弧度
1、对于一些特殊角的度数与弧度数之间的换算要熟记。
说明:
2、用弧度为单位表示角的大小时, “弧度”二字通常省略不写,但
用“度”(°)为单位不能省。
3、用弧度为单位表示角时,通常写 成“多少π”的形式。如无特别
要求,不用将π化成小数。
新知讲解
计算并填写下列表格
新知讲解
在弧度制下,角的集合与实数集之间建立了一一对应关系:即每一个
角都有唯一的一个实数(即这个角的弧度数)与它对应;反过来,每一个
实数也都有唯一的一个角(即弧度数等于这个实数的角)与它对应.
正角
负角
零角
正数
负数
0
任意角的集合
实数集R
合作探究
例1、把67°30′化成弧度。
解:
例2、把 —π 弧度化成度。
5
3
解:
合作探究
例3、用弧度制表示
(1)终边落在45°角的终边上的所有角的集合
例2、把 3.14rad化成度.(精确到0.001)
解:
解:
合作探究
例4、利用弧度制证明下列关于扇形的公式:
(1) (2) (3)
其中r 是圆的半径,α(0<α<2π)为圆心角,l是扇形的弧长,S是扇形的面积.
解:(1)由弧度的定义: 易得:
(2)由
(3)上式中,αr=l代入面积S,即
新知讲解
弧度制下的弧长和扇形面积公式
由弧度的定义式:
nπR2
360
S= ———
得弧长公式:
由扇形面积
相比初中所学的弧长公式 : 和扇形面积公式:
在形式上简单的多。
(0<α<2π)
其中,ɑ为圆心角,r为半径, 为弧长。
合作探究
例5、已知扇形的周长为10cm, 面积为4cm2,求扇形的中心角.
解:设扇形的中心角的弧度数为 , 弧长为l,半径为R,
依题意:
由①得 ,
代入②得
舍去
当R=1时,l=8cm时,
当R=4时,l=2cm时,
课堂练习
1、已知扇形所在圆半径为5,圆心角为135°,求扇形面积。
解:
2、已知扇形的周长为20cm,当扇形的中心角为多大时,它有最大面积?
解:设圆半径为R, 则
3、把下列各角化成 的形式:
(1) ; (2) ; (3) .
(1):
(3):
(2):
解:
课堂练习
课堂总结
弧度制定义:
长度等于半径长的圆弧所对的圆心角叫做1弧度(radian)的角,
用符号rad表示,读作弧度.
弧度与角度的互化:
1°= —— 弧度 ≈ 0.01745弧度
180
π
1弧度 =( ——)°≈ 57.30°= 57°18′
π
180
弧度制下的弧长和扇形面积公式
度 00 300 450 1200 1350 1500 3600
弧度
板书设计
(2)弧度与角度的互化.
(1)弧度的定义
1°= —— 弧度 ≈ 0.01745弧度
180
π
1弧度 =( ——)°
≈ 57.30°= 57°18′
π
180
(3)弧度制下的弧长
和扇形面积公式
作业布置
1、已知扇形所在圆半径为5,圆心角 为135°,求扇形面积。
2、已知扇形的周长为20cm,当扇形的中心角为多大时,它有最大面积?
3、课本P175练习1、2、3、5、6
https://www.21cnjy.com/help/help_extract.php
5.1.2弧度制
人教A(2019)版
必修一
新知导入
复习巩固
一、任意角:
正角:逆时针方向旋转
负角:顺时针方向旋转
零角:没有旋转
二、角的度量:
把圆周平均分成360等份,每
一份所对的中心角叫一度。
1°
三、初中在度这个度量单位下的弧长和面积公式:
nπR2
360
S= ———
弧长
扇形面积
新知讲解
角度制这种计量方法是古巴比伦人发明的,是将圆周平均分成360等份
把一份定义为一度,是一个几何概念,有明显的直观性,比如900是圆周的
四分之一,是直角;1800圆周的一半是平角等等很多特殊角的角度都是整数
等优点,但也存在明显的不足,(1)在研究以角为自变量的函数时,自变量和
函数值都应是两个实数集合,以角度计量显然不满足这个条件;(2)从前面学
过的弧长和扇形面积公式可以看出,使用角度制这些公式比较繁琐。
随着学习的不断深入,我们会发现角度制计量方法有很多不便之处,为
了解决这些问题,英国数学家罗杰·柯特斯Roger Cotes在1714年提出弧度制的
概念。
新知讲解
弧度制的概念
弧度制定义:
长度等于半径长的圆弧所对的圆心角叫做1弧度(radian)的角,
用符号rad表示,读作弧度.
这种以弧度为单位来度量角的单位制叫做弧度制。
1弧度
r
l=r
O
A
B
2弧度
O
A
B
l=2r
B
3弧度
O
A
l=3r
可见,圆心角的弧度数就是所对弧长与半径的比值。
新知讲解
为什么可以用弧长与其半径的比值来度量角的大小呢?即这个比值
是否与所取的圆的半径大小无关呢?
我们从初中所学的弧长公式 中可以得到答案:
将公式变形为:
我们发现如果角确定后,弧长与半径的比值是一个确定的值,而
不随弧长与半径的改变而改变。
A
B
A'
B'
一般地,我们规定:正角的弧度数为正数,负角的弧度数为负数,零角的弧度数为0,如果半径为r的圆的圆心角α所对弧的长为l,那么角α的弧度数的绝对值是
︱α︱=
l
r
α的正负由角α的终边的旋转方向决定
弧度与角度的互化
新知讲解
将角度α化为弧度数β:
由弧长公式:
将弧度 度α化为角度数β:
由弧长公式:
1°= —— 弧度 ≈ 0.01745弧度
180
π
1弧度 =( ——)°≈ 57.30°= 57°18′
π
180
3600=2π弧度
圆周的弧长l=2πr,周角3600,所以,3600=
1800=π弧度
度 00 300 450 1200 1350 1500 3600
弧度
1、对于一些特殊角的度数与弧度数之间的换算要熟记。
说明:
2、用弧度为单位表示角的大小时, “弧度”二字通常省略不写,但
用“度”(°)为单位不能省。
3、用弧度为单位表示角时,通常写 成“多少π”的形式。如无特别
要求,不用将π化成小数。
新知讲解
计算并填写下列表格
新知讲解
在弧度制下,角的集合与实数集之间建立了一一对应关系:即每一个
角都有唯一的一个实数(即这个角的弧度数)与它对应;反过来,每一个
实数也都有唯一的一个角(即弧度数等于这个实数的角)与它对应.
正角
负角
零角
正数
负数
0
任意角的集合
实数集R
合作探究
例1、把67°30′化成弧度。
解:
例2、把 —π 弧度化成度。
5
3
解:
合作探究
例3、用弧度制表示
(1)终边落在45°角的终边上的所有角的集合
例2、把 3.14rad化成度.(精确到0.001)
解:
解:
合作探究
例4、利用弧度制证明下列关于扇形的公式:
(1) (2) (3)
其中r 是圆的半径,α(0<α<2π)为圆心角,l是扇形的弧长,S是扇形的面积.
解:(1)由弧度的定义: 易得:
(2)由
(3)上式中,αr=l代入面积S,即
新知讲解
弧度制下的弧长和扇形面积公式
由弧度的定义式:
nπR2
360
S= ———
得弧长公式:
由扇形面积
相比初中所学的弧长公式 : 和扇形面积公式:
在形式上简单的多。
(0<α<2π)
其中,ɑ为圆心角,r为半径, 为弧长。
合作探究
例5、已知扇形的周长为10cm, 面积为4cm2,求扇形的中心角.
解:设扇形的中心角的弧度数为 , 弧长为l,半径为R,
依题意:
由①得 ,
代入②得
舍去
当R=1时,l=8cm时,
当R=4时,l=2cm时,
课堂练习
1、已知扇形所在圆半径为5,圆心角为135°,求扇形面积。
解:
2、已知扇形的周长为20cm,当扇形的中心角为多大时,它有最大面积?
解:设圆半径为R, 则
3、把下列各角化成 的形式:
(1) ; (2) ; (3) .
(1):
(3):
(2):
解:
课堂练习
课堂总结
弧度制定义:
长度等于半径长的圆弧所对的圆心角叫做1弧度(radian)的角,
用符号rad表示,读作弧度.
弧度与角度的互化:
1°= —— 弧度 ≈ 0.01745弧度
180
π
1弧度 =( ——)°≈ 57.30°= 57°18′
π
180
弧度制下的弧长和扇形面积公式
度 00 300 450 1200 1350 1500 3600
弧度
板书设计
(2)弧度与角度的互化.
(1)弧度的定义
1°= —— 弧度 ≈ 0.01745弧度
180
π
1弧度 =( ——)°
≈ 57.30°= 57°18′
π
180
(3)弧度制下的弧长
和扇形面积公式
作业布置
1、已知扇形所在圆半径为5,圆心角 为135°,求扇形面积。
2、已知扇形的周长为20cm,当扇形的中心角为多大时,它有最大面积?
3、课本P175练习1、2、3、5、6
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
